IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 8.2 – Thermal energy Transfer
Topic 8 Weightage : 7 %
All Questions for Topic 8.2 – Conduction, convection and thermal radiation , Black-body radiation , Albedo and emissivity , The solar constant , The greenhouse effect , Energy balance in the Earth surface–atmosphere system
Question
In a simple climate model for a planet, the incoming intensity is 400 W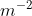 
and the radiated intensity is 300 W .
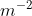The temperature of the planet is constant. What are the reflected intensity from the planet and the albedo of the planet?
Ans: | Reflected intensity from the planet | Albedo of the planet |
A | 100 W | 0.25 |
B | 100 W | 0.75 |
C | 300 W | 0.25 |
D | 300 W | 0.75 |
▶️Answer/Explanation
Ans: A
Since Temperature of temperature of the planet is constant hence
\(\Delta Q = mc\Delta T =0\)
\(\Rightarrow \) Total Incoming Intensity = Out going Intensity
Hence
\(400 = 300 + \text {reflected Intensity}\)
Hence
\(\text {reflected Intensity} = 100\; Wm^{-2}\)
\(albedo =\alpha =\frac{\text{total scattered power}}{\text{total incident power}}\)
Total scattered (reflected) Intensity \(= 100 \; W m^{-2}\)
and Total incident Intensity \(= 400 \; W m^{-2}\)
or
Total scattered (reflected) Power \(= 100 \times A \; \; W \) A= Surface arean of planet
Total incident Power = \(400 \times A \; W\)
Hence
\(albedo =\alpha =\frac{\text{total scattered power}}{\text{total incident power}}\)
\(=\frac{100 \times A}{400 \times A} =0.25\)
Question
A black body at temperature T emits radiation with peak wavelength and power P. What is the temperature of the black body and the power emitted for a peak wavelength of
?
Ans: | Temperature of the black body | Power emitted by the black body |
A | ||
B | ||
C | 2T | 4P |
D | 2T | 16P |
▶️Answer/Explanation
Ans: D
Radiation is the transfer of energy through electromagnetic radiation.
Most energy is radiated at a specific wavelength \(\lambda_m\) determined by Wien’s displacement law:
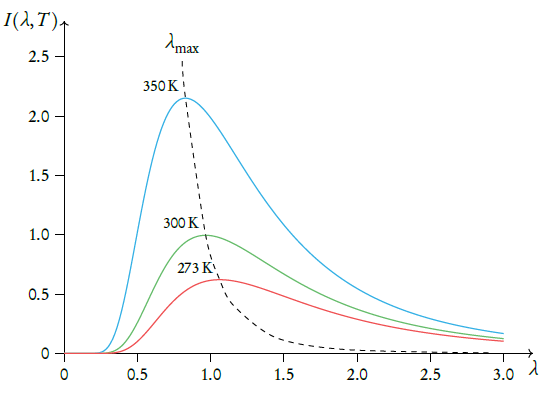
\(\lambda_m T= Constant = 2.9 \times 10^{-3}\)
where
\(\lambda_m =\) wavelength for which maximum intensity
\(T\) =temperature in kelvin
Hence in this given question
\(\lambda_mT =constant\)
or
\(\lambda_pT=\frac{\lambda_p}{2}T’\)
or
\(T’ = 2T\)
Black-body radiation The power radiated by a body is governed by Stefan-Boltzman law
\(P=\varepsilon \sigma AT^4\)
Where
\(P= power\)
\(\varepsilon =emissivity = 1 \) for Black body
\(\sigma =\) Stefan-Boltzmann constant
A= Area
T = temperature
Hence every other parameter remain constant , as per given question
\(P = k T^4\)
hence
\(\frac{P’}{P}=\frac{T’^4}{T^4}\)
Now \(T’ = 2T\)
Hence
\(\frac{P’}{P}=\frac{(2T)^4}{T^4} =2^4=16\)
Hence \(P’ = 16\)
Question
Mars and Earth act as black bodies. The \(\frac{{{\text{power radiated by Mars}}}}{{{\text{power radiated by the Earth}}}} = p\) and \(\frac{{{\text{absolute mean temperature of the surface of Mars}}}}{{{\text{absolute mean temperature of the surface of the Earth}}}} = t\).
What is the value of \(\frac{{{\text{radius of Mars}}}}{{{\text{radius of the Earth}}}}\)?
A. \(\frac{p}{{{t^4}}}\)
B. \(\frac{{\sqrt p }}{{{t^2}}}\)
C. \(\frac{{{t^4}}}{p}\)
D. \(\frac{{{t^2}}}{{\sqrt p }}\)
▶️Answer/Explanation
Markscheme
B
Black-body radiation The power radiated by a body is governed by Stefan-Boltzman law
\(P=\varepsilon \sigma AT^4\)
Where
\(P= power\)
\(\varepsilon =emissivity = 1 \) for Black body
\(\sigma =\) Stefan-Boltzmann constant
\(A= Area =4\pi r^2\)
T = temperature
as per given question emissivity = 1 as planets are black bodies
\(\frac{P_{Mars}}{P_{Earth}}=\frac{\sigma \times 4\pi (R_{Mars})^2\times (T_{Mars})^4}{\sigma \times 4\pi (R_{Earth})^2\times (T_{Earth})^4}\)
\(= \frac{(R_{Mars})^2\times (T_{Mars})^4}{(R_{Earth})^2\times (T_{Earth})^4}\)
Now
\(\frac{P_{Mars}}{P_{Earth}} =p \; and\; \frac{T_{Mars}}{T_{Earth}} =t\)
Putting these values in above equation , we get
\(\frac{(R_{Mars})^2}{(R_{Earth})^2}\times t^4=p\)
or
\(\frac{R_{Mars}}{R_{Earth}}=\sqrt{\frac{p}{t^4}}=\frac{\sqrt{p}}{t^2}\)
Question
Three gases in the atmosphere are
I. carbon dioxide (CO2)
II. dinitrogen monoxide (N2O)
III. oxygen (O2).
Which of these are considered to be greenhouse gases?
A. I and II only
B. I and III only
C. II and III only
D. I, II and III
▶️Answer/Explanation
Markscheme
A
Greenhouse gases strongly absorb infrared radiation from the atmosphere, when re-radiated in all directions, these gases account for additional warming. These gases include water vapour, carbon dioxide, methane and nitrous oxide.
Question
A black body emits radiation with its greatest intensity at a wavelength of Imax. The surface temperature of the black body doubles without any other change occurring. What is the wavelength at which the greatest intensity of radiation is emitted?
A. Imax
B. \(\frac{{{\text{I}}{{\text{}}_{{\text{max}}}}}}{{\text{2}}}\)
C. \(\frac{{{\text{I}}{{\text{}}_{{\text{max}}}}}}{{\text{4}}}\)
D. \(\frac{{{\text{I}}{{\text{}}_{{\text{max}}}}}}{{\text{16}}}\)
▶️Answer/Explanation
Markscheme
B
\(\lambda_m T= Constant = 2.9 \times 10^{-3}\)
where
\(\lambda_m =\) wavelength for which maximum intensity
\(T\) =temperature in kelvin
Given in question
Initial condition
\(\lambda_m = I_{}max \) , Temperature = \(T\)
2nd Condition
\(\lambda_m =? \) , temperature = \(2T\)
Hence
\(I_{max}T=\lambda_m \times 2T\)
\(\lambda_m=\frac{I_{max}T}{2T} =\frac{I_{max}}{2}\)
Related Links