IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 9.1 Simple harmonic motion
Topic 9 Weightage : 5 %
All Questions for Topic 9.1 – The defining equation of SHM , Energy changes
The ball is now displaced through a small distance x from the bottom of the bowl and is then released from rest.
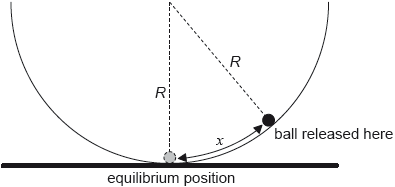
The magnitude of the force on the ball towards the equilibrium position is given by
\[\frac{{mgx}}{R}\]
where R is the radius of the bowl.
d.i.
Outline why the ball will perform simple harmonic oscillations about the equilibrium position.[1]
Show that the period of oscillation of the ball is about 6 s.[2]
The amplitude of oscillation is 0.12 m. On the axes, draw a graph to show the variation with time t of the velocity v of the ball during one period.
 [3]
[3]
▶️Answer/Explanation
Markscheme
d.i.
the «restoring» force/acceleration is proportional to displacement
Direction is not required
[1 mark]
ω = «\(\sqrt {\frac{g}{R}} \)» = \(\sqrt {\frac{{9.81}}{{8.0}}} \) «= 1.107 s–1»
T = «\(\frac{{2\pi }}{\omega }\) = \(\frac{{2\pi }}{{1.107}}\) =» 5.7 «s»
Allow use of or g = 9.8 or 10
Award [0] for a substitution into T = 2π\(\sqrt {\frac{I}{g}} \)
[2 marks]
sine graph
correct amplitude «0.13 m s–1»
correct period and only 1 period shown
Accept ± sine for shape of the graph. Accept 5.7 s or 6.0 s for the correct period.
Amplitude should be correct to ±\(\frac{1}{2}\) square for MP2
eg: v /m s–1 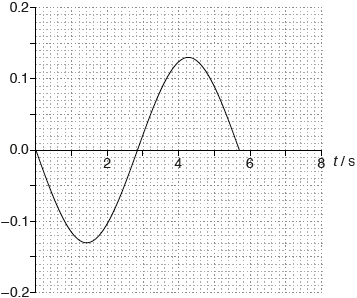
[3 marks]
An elastic climbing rope is tested by fixing one end of the rope to the top of a crane. The other end of the rope is connected to a block which is initially at position A. The block is released from rest. The mass of the rope is negligible.
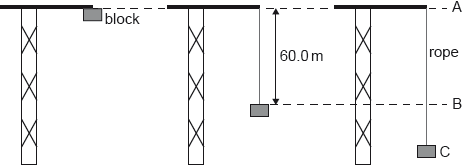
The unextended length of the rope is 60.0 m. From position A to position B, the block falls freely.
In another test, the block hangs in equilibrium at the end of the same elastic rope. The elastic constant of the rope is 400 Nm–1. The block is pulled 3.50 m vertically below the equilibrium position and is then released from rest.
e.i.
Calculate the time taken for the block to return to the equilibrium position for the first time.[2]
Calculate the speed of the block as it passes the equilibrium position.[2]
▶️Answer/Explanation
Markscheme
e.i.
T = 2π\(\sqrt {\frac{{80.0}}{{400}}} \) = 2.81 «s»
time = \(\frac{T}{4}\) = 0.702 «s»
Award [0] for kinematic solutions that assume a constant acceleration.
[2 marks]
ALTERNATIVE 1
ω = \(\frac{{2\pi }}{{2.81}}\) = 2.24 «rad s–1»
v = 2.24 × 3.50 = 7.84 «ms–1»
ALTERNATIVE 2
\(\frac{1}{2}\)kx2 = \(\frac{1}{2}\)mv2 OR \(\frac{1}{2}\)400 × 3.52 = \(\frac{1}{2}\)80v2
v = 7.84 «ms–1»
Award [0] for kinematic solutions that assume a constant acceleration.
Allow ECF for T from (e)(i).
[2 marks]
There is a proposal to power a space satellite X as it orbits the Earth. In this model, X is connected by an electronically-conducting cable to another smaller satellite Y.
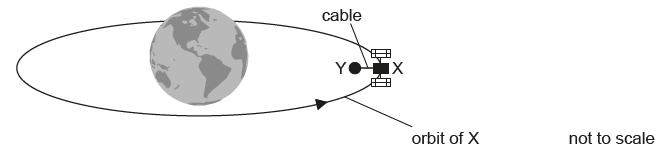
Satellite Y orbits closer to the centre of Earth than satellite X. Outline why
The cable acts as a spring. Satellite Y has a mass m of 3.5 x 102 kg. Under certain circumstances, satellite Y will perform simple harmonic motion (SHM) with a period T of 5.2 s.
a.
Satellite X orbits 6600 km from the centre of the Earth.
Mass of the Earth = 6.0 x 1024 kg
Show that the orbital speed of satellite X is about 8 km s–1.[2]
the orbital times for X and Y are different.[1]
satellite Y requires a propulsion system.[2]
The cable between the satellites cuts the magnetic field lines of the Earth at right angles.
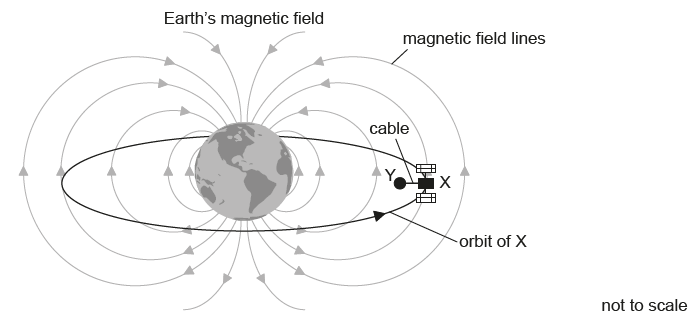
Explain why satellite X becomes positively charged.[3]
Satellite X must release ions into the space between the satellites. Explain why the current in the cable will become zero unless there is a method for transferring charge from X to Y.[3]
The magnetic field strength of the Earth is 31 μT at the orbital radius of the satellites. The cable is 15 km in length. Calculate the emf induced in the cable.[2]
Estimate the value of k in the following expression.
T = \(2\pi \sqrt {\frac{m}{k}} \)
Give an appropriate unit for your answer. Ignore the mass of the cable and any oscillation of satellite X.[3]
Describe the energy changes in the satellite Y-cable system during one cycle of the oscillation.[2]
▶️Answer/Explanation
Markscheme
a.
«\(v = \sqrt {\frac{{G{M_E}}}{r}} \)» = \(\sqrt {\frac{{6.67 \times {{10}^{ – 11}} \times 6.0 \times {{10}^{24}}}}{{6600 \times {{10}^3}}}} \)
7800 «m s–1»
Full substitution required
Must see 2+ significant figures.
Y has smaller orbit/orbital speed is greater so time period is less
Allow answer from appropriate equation
Allow converse argument for X
to stop Y from getting ahead
to remain stationary with respect to X
otherwise will add tension to cable/damage satellite/pull X out of its orbit
cable is a conductor and contains electrons
electrons/charges experience a force when moving in a magnetic field
use of a suitable hand rule to show that satellite Y becomes negative «so X becomes positive»
Alternative 2
cable is a conductor
so current will flow by induction flow when it moves through a B field
use of a suitable hand rule to show current to right so «X becomes positive»
Marks should be awarded from either one alternative or the other.
Do not allow discussion of positive charges moving towards X
electrons would build up at satellite Y/positive charge at X
preventing further charge flow
by electrostatic repulsion
unless a complete circuit exists
«ε = Blv =» 31 x 10–6 x 7990 x 15000
3600 «V»
Allow 3700 «V» from v = 8000 m s–1.
use of k = «\(\frac{{4{\pi ^2}m}}{{{T^2}}} = \)» \(\frac{{4 \times {\pi ^2} \times 350}}{{{{5.2}^2}}}\)
510
N m–1 or kg s–2
Allow MP1 and MP2 for a bald correct answer
Allow 500
Allow N/m etc.
Ep in the cable/system transfers to Ek of Y
and back again twice in each cycle
Exclusive use of gravitational potential energy negates MP1