Question
A particle executes simple harmonic motion (SHM) with period T.
Which sketch graph correctly shows how the total energy E of the particle varies with time t from t = 0 to \(t = \frac{T}{2}\)?
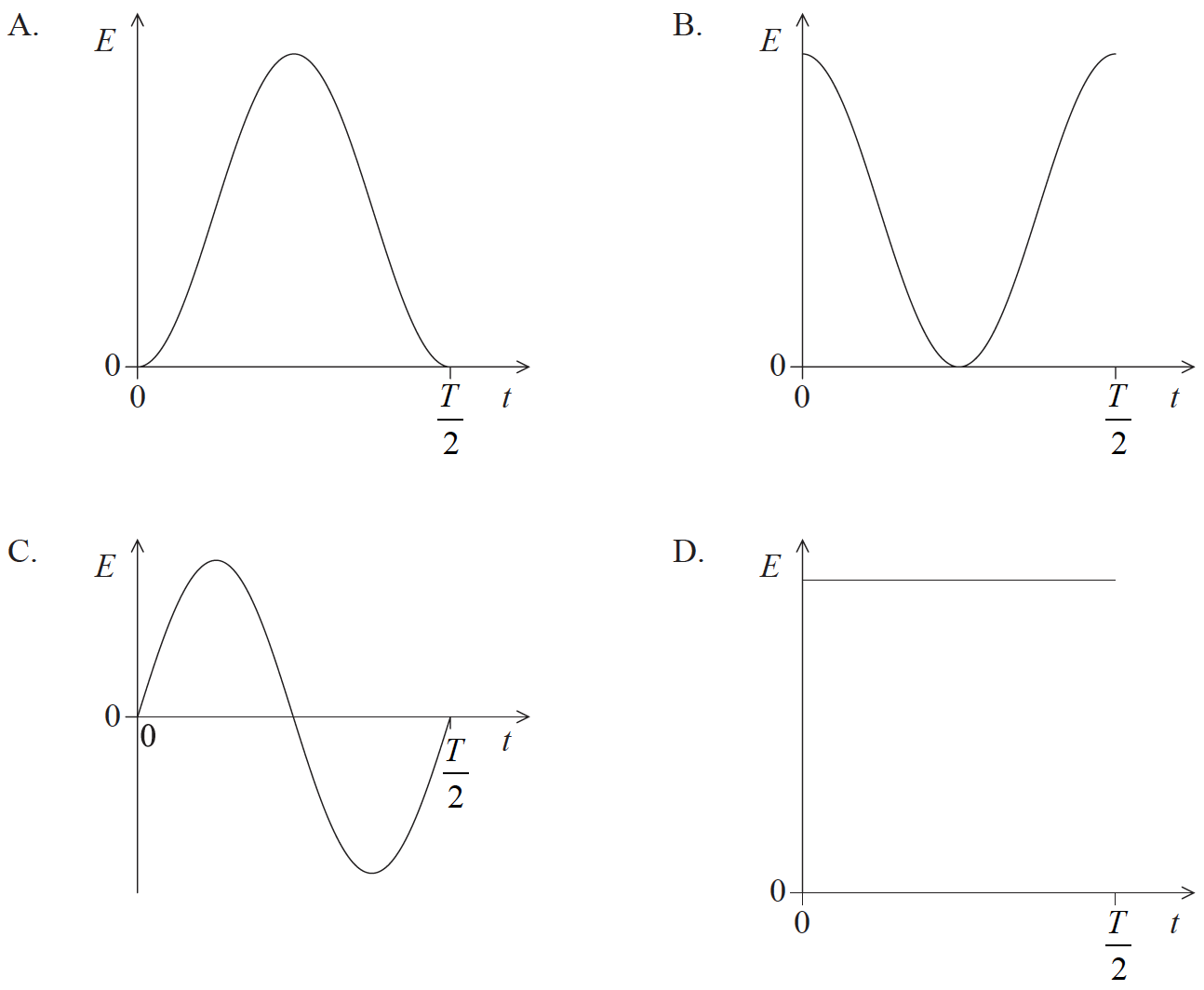
Answer/Explanation
Markscheme
D
Total Energy is constant.
Question
A particle of mass \(m\) oscillates with simple harmonic motion (SHM) of angular frequency \(\omega \). The amplitude of the SHM is \(A\). What is the kinetic energy of the particle when it is half way between the equilibrium position and one extreme of the motion?
A. \(\frac{{m{A^2}{\omega ^2}}}{4}\)
B. \(\frac{{3m{A^2}{\omega ^2}}}{8}\)
C. \(\frac{{9m{A^2}{\omega ^2}}}{{32}}\)
D. \(\frac{{15m{A^2}{\omega ^2}}}{{32}}\)
Answer/Explanation
Markscheme
B
Kinetic energy : A particle in S.H.M. possesses kinetic energy by virtue of its motion.
= \(K(t)=\frac{1}{2}mv^2 =\frac{1}{2}mw^2x_m^2sin^2(wt+\phi )\)Given in the question \(y=\frac{A}{2}\)
\(\therefore K.E = \frac{1}{2}mw^2(A^2-(\frac{A}{2})^2 )\)
\(=\frac{3}{8}mw^2A^2\)
\(\therefore K.E = \frac{1}{2}mw^2(A^2-(\frac{A}{2})^2 )\)
\(=\frac{3}{8}mw^2A^2\)
Related Links