This question is about the Doppler effect.
The diagram shows wavefronts in air produced by a stationary source S of sound. The distance between successive wavefronts is equal to the wavelength of the sound. The speed of sound is c.
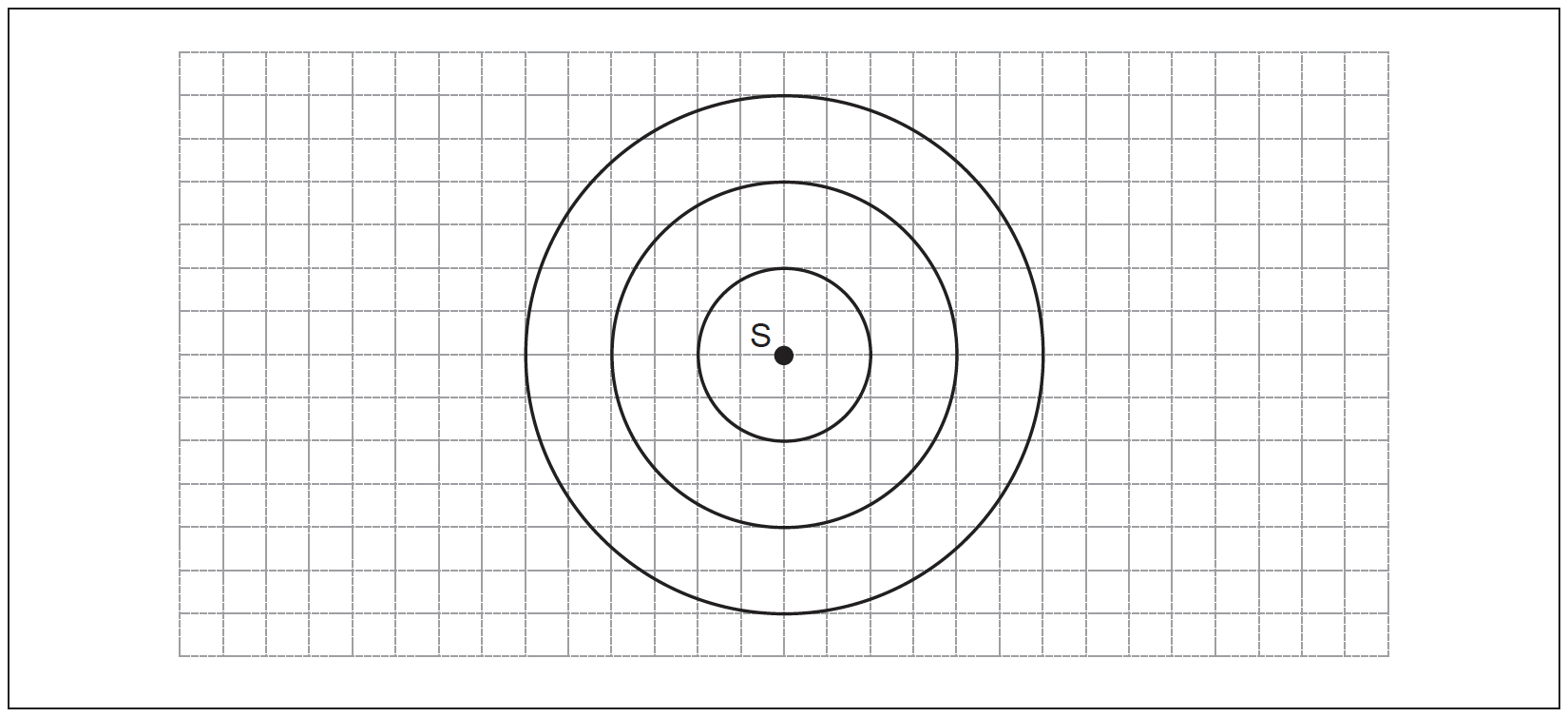
a.On the diagram, sketch three successive wavefronts produced when S is moving to the left at a speed of 0.5c.[2]

(i) Determine the speed of a point on the edge of the turntable.
(ii) State the assumption you made in your answer to (b)(i).[3]
▶️Answer/Explanation
Markscheme
a.
3 circular wavefronts;
2 centres/sources of wavefronts move left (by one box);
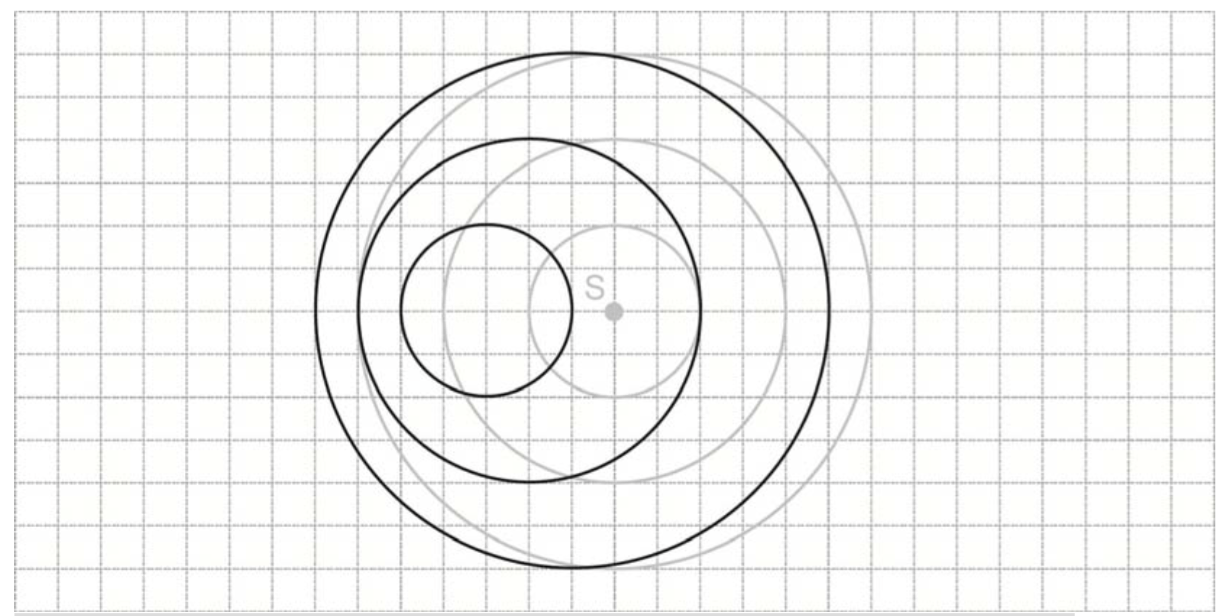
Drawn circular wavefronts may be larger as in diagram here, or could be equal sized. Both are acceptable.
(i) \(v = \frac{{5 \times {{10}^{ – 16}} \times 3 \times {{10}^8}}}{{7.5 \times {{10}^{ – 9}}}}\);
20(ms–1);
Use of sound equation not acceptable.
(ii) assume speed of X-rays \( = \) c / assume speed of turntable << c;
This question is about the Doppler effect.
Georgia carries out an experiment to measure the speed of mosquitoes. She sets up a microphone to record the sounds of passing mosquitoes.
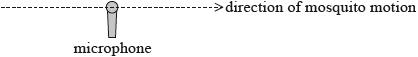
One mosquito is moving in a straight line with constant speed and passes very close to the microphone as seen in the diagram. The mosquito produces a sound of constant frequency.
a.The speed of sound in air is \({\text{340 m}}\,{{\text{s}}^{ – {\text{1}}}}\).
The maximum frequency recorded is 751 Hz and the minimum frequency recorded is 749 Hz. Explain this observation.[2]
▶️Answer/Explanation
Markscheme
a.
as the mosquito approaches the wavelength perceived by Georgia is shorter and therefore the perceived frequency is higher;
as the mosquito is moving away, the wavelength perceived is longer than the emitted and therefore the perceived frequency is lower;
due to the Doppler effect;
approaching \(751 = f \times \frac{{340}}{{340 – u}}\);
moving away \(749 = f \times \frac{{340}}{{340 + u}}\);
to produce \(u = 0.45{\text{ m}}\,{{\text{s}}^{ – 1}}\);
or
emitted frequency is \(\frac{{751 + 749}}{2} = 750{\text{ Hz}}\);
applying the Doppler effect for approach (or recession), \(751 = 750\frac{{340}}{{340 – u}}\)\(\,\,\,\)or\(\,\,\,\)\(749 = 750\frac{{340}}{{340 + u}}\);
to produce \(u = 0.45{\text{ m}}\,{{\text{s}}^{ – 1}}\);