Question
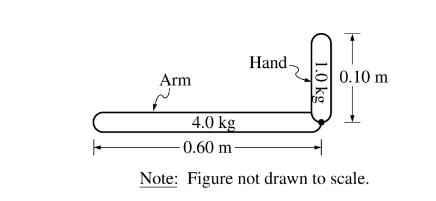
The arm is held in the horizontal position and the hand is bent at the wrist so the fingers point up, as shown in the figure above. The torque exerted by the weight of the hand with respect to the shoulder is most nearly
(A) 6 N .m
(B) 10 N .m
(C) 30 N. m
(D) 60 N. m
(E) 70 N .m
Answer/Explanation
Question
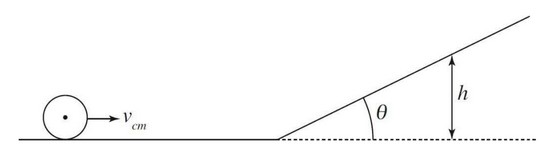
The center of mass of a cylinder of mass m, radius r, and rotational inertia \(I = \frac{1}{2} mr^2\) has a velocity of \(v_{cm}\) as it rolls without slipping along a horizontal surface. It then encounters a ramp of angle \(\theta \), and continues to roll up the ramp without slipping.
What is the maximum height the cylinder reaches ?
(A) \(\frac{v^2}{4g}\)
(B) \(\frac{4v^2}{3g}\)
(C) \(\frac{v^2}{3g}\)
(D) \(\frac{3v^2}{4g}\)
(E) \(\frac{4g}{3v^2}\)
Answer/Explanation
Ans: D
We will use the Law of Conservation of Energy for this problem. The cylinder has rotational and translational kinetic energy as it rolls along the horizontal surface. All of that energy will be converted into gravitational potential energy when it reaches its maximum height up the ramp.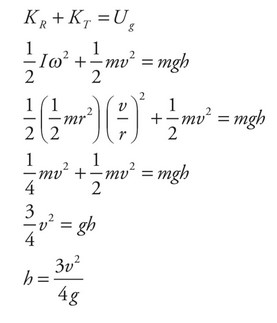
Question
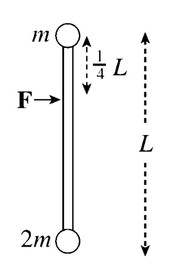
The figure shows a view from above of two objects attached to the end of a rigid massless rod at rest on a frictionless table. When a force F is applied as shown, the resulting rotational acceleration
of the rod about its center of mass is kF/(mL). What is k?
(A) \(\frac{3}{8}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{5}{8}\)
(D) \(\frac{3}{4}\)
(E) \(\frac{5}{6}\)
Answer/Explanation
Ans: C
The center of mass of the system is at a distance of
\(y_{cm}=\frac{(m)(0) + (2m)(L)}{m +2m} = \frac{2}{3} L\)
below the mass m. With respect to this point, the clockwise torque produced by the force F has magnitude
\(\tau = rF = (\frac{2}{3}L – \frac{1}{4} L) F = \frac{5}{12} LF\)
Since the rotational inertia of the system about its center of mass is
\(I = \sum m_i r_i^2 = m (\frac{2}{3}L)^2 + (2m) (\frac{1}{3}L)^2 = \frac{2}{3} mL^2\)
the equation \(\tau = Ia\) becomes