Question
(a) The centres of two identical fixed conducting spheres each of charge \(+Q\) are separated by a distance \(D\). C is the midpoint of the line joining the centres of the spheres.

(i) Sketch, on the axes, how the electric potential \(V\) due to the two charges varies with the distance \(r\) from the centre of the left charge. No numbers are required. Your graph should extend from \(r=0\) to \(r=D\). [3]

(ii) Calculate the work done to bring a small charge \(q\) from infinity to point \(C\).
Data given:
$
\begin{aligned}
& Q=2.0 \times 10^{-3} \mathrm{C}, \\
& q=4.0 \times 10^{-9} \mathrm{C} \\
& D=1.2 \mathrm{~m}
\end{aligned}
$
(b) The small positive charge \(q\) is placed a distance \(x\) to the right of \(\mathrm{C}\). The distance \(x\) is very small compared to \(D\).

(i) The magnitude of the net force on \(q\) is given by \(\frac{32 k Q q}{D^3} x\). Explain why the charge \(q\) will execute simple harmonic oscillations about \(C\).[2]
(ii) The mass of the charge \(q\) is \(0.025 \mathrm{~kg}\).
Calculate the angular frequency of the oscillations using the data in (a)(ii) and the expression in (b)(i).[2]
(c) The charges \(Q\) are replaced by neutral masses \(M\) and the charge \(q\) by a neutral mass \(m\). The mass \(m\) is displaced away from \(C\) by a small distance \(x\) and released. Discuss whether the motion of \(m\) will be the same as that of \(q\). [2]
▶️Answer/Explanation
Ans:
Constant, non-zero within spheres
A clear, non-zero positive minimum at \(\mathrm{C} \checkmark\)
Symmetric bowl shaped up curved shape in between \(\checkmark\)
ii \(\begin{aligned} & V_{\ll}=2 \times \frac{8.99 \times 10^9 \times 2.0 \times 10^{-3}}{0.60} \ggg=6.0 \times 10^7 \& V_» \\ & W=\ll q V=6.0 \times 10^7 \times 4.0 \times 10^{-9}=» 0.24 \ll J »\end{aligned}\)
b i The restoring force/acceleration is opposite to the displacement/towards equilibrium / OWTTE \(\checkmark\)
and proportional to displacement from equilibrium / OWTTE \(\checkmark\)
ii \(\begin{aligned} & \omega=\sqrt{\frac{32 k Q q}{m D^3}} \text { OR use of } F=m \omega^2 r \text { OR } F=1.33 \times \text { OR } a=53.3 \times \\ & \kappa=\sqrt{\frac{32 \times 8.99 \times 10^9 \times 2.0 \times 10^{-3} \times 4.0 \times 10^{-9}}{0.025 \times 1.2^3}},=7.299 \ll \mathrm{S}^{-1} w\end{aligned}\)
c.the net force will no longer be a restoring force/directed towards equilibrium
OR
the gravitational force is attractive/neutral mass would be pulled towards larger masses/OWTTE \(\checkmark\)
«and sow no, motion will not be the same/no longer be SHM / OWTTE \(\checkmark\)
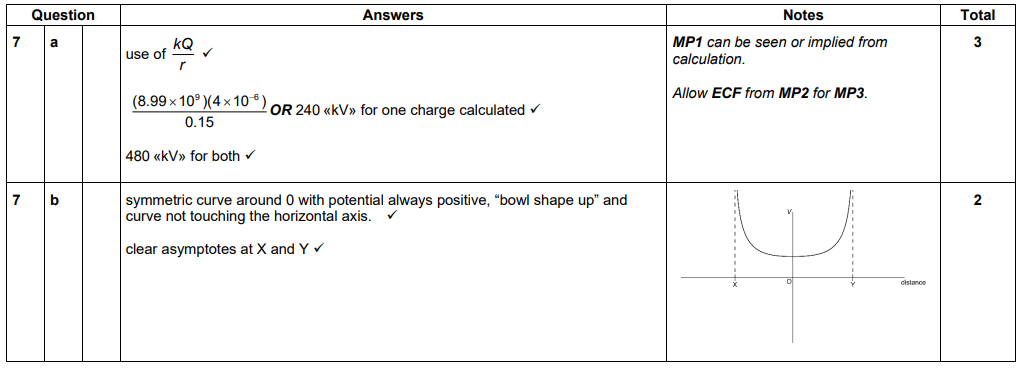
Question
Two identical positive point charges X and Y are placed 0.30m apart on a horizontal line.
O is the point midway between X and Y. The charge on X and the charge on Y is +4.0µC.
(a) Calculate the electric potential at O. [3]
(b) Sketch, on the axes, the variation of the electric potential V with distance between
X and Y. [2]

(c) A positive charge Z is released from rest 0.010m from O on the line between X and Y.
Z then begins to oscillate about point O.

(i) Identify the direction of the resultant force acting on Z as it oscillates. [2]
(ii) Deduce whether the motion of Z is simple harmonic. [2]
Answer/Explanation
Ans.