The ball is now displaced through a small distance x from the bottom of the bowl and is then released from rest.
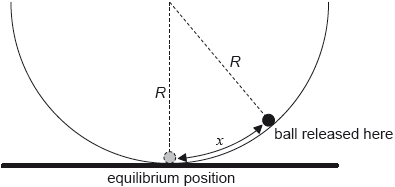
The magnitude of the force on the ball towards the equilibrium position is given by
\[\frac{{mgx}}{R}\]
where R is the radius of the bowl.
d.i.
Outline why the ball will perform simple harmonic oscillations about the equilibrium position.
Show that the period of oscillation of the ball is about 6 s.
The amplitude of oscillation is 0.12 m. On the axes, draw a graph to show the variation with time t of the velocity v of the ball during one period.
Answer/Explanation
Markscheme
d.i.
the «restoring» force/acceleration is proportional to displacement
Direction is not required
[1 mark]
ω = «\(\sqrt {\frac{g}{R}} \)» = \(\sqrt {\frac{{9.81}}{{8.0}}} \) «= 1.107 s–1»
T = «\(\frac{{2\pi }}{\omega }\) = \(\frac{{2\pi }}{{1.107}}\) =» 5.7 «s»
Allow use of or g = 9.8 or 10
Award [0] for a substitution into T = 2π\(\sqrt {\frac{I}{g}} \)
[2 marks]
sine graph
correct amplitude «0.13 m s–1»
correct period and only 1 period shown
Accept ± sine for shape of the graph. Accept 5.7 s or 6.0 s for the correct period.
Amplitude should be correct to ±\(\frac{1}{2}\) square for MP2
eg: v /m s–1 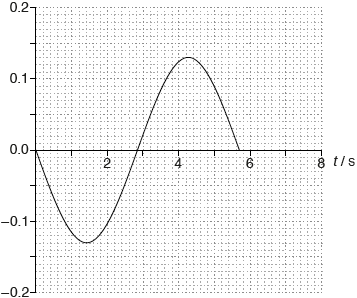
[3 marks]
A beam of coherent monochromatic light from a distant galaxy is used in an optics experiment on Earth.
The beam is incident normally on a double slit. The distance between the slits is 0.300 mm. A screen is at a distance D from the slits. The diffraction angle θ is labelled.
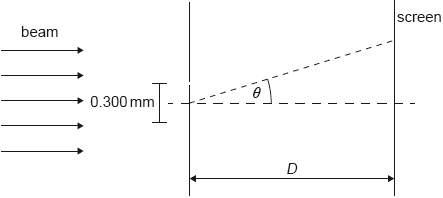
The graph of variation of intensity with diffraction angle for this experiment is shown.
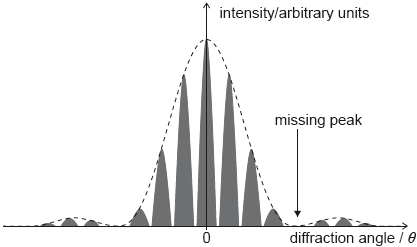
a.ii.
Outline why the beam has to be coherent in order for the fringes to be visible.[1]
Calculate the angular separation between the central peak and the missing peak in the double-slit interference intensity pattern. State your answer to an appropriate number of significant figures.[3]
Deduce, in mm, the width of one slit.[2]
The wavelength of the light in the beam when emitted by the galaxy was 621.4 nm.
Explain, without further calculation, what can be deduced about the relative motion of the galaxy and the Earth.[2]
Answer/Explanation
Markscheme
a.ii.
light waves (from slits) must have constant phase difference / no phase difference / be in phase
OWTTE[1 mark]
sin θ = \(\frac{{4 \times 633.0 \times {{10}^{ – 9}}}}{{0.300 \times {{10}^{ – 3}}}}\)
sin θ = 0.0084401…
final answer to three sig figs (eg 0.00844 or 8.44 × 10–3)
Allow ECF from (a)(iii).
Award [1] for 0.121 rad (can award MP3 in addition for proper sig fig)
Accept calculation in degrees leading to 0.481 degrees.
Award MP3 for any answer expressed to 3sf.[3 marks]
use of diffraction formula «b = \(\frac{\lambda }{\theta }\)»
OR
\(\frac{{633.0 \times {{10}^{ – 9}}}}{{0.00844}}\)
«=» 7.5«00» × 10–2 «mm»
Allow ECF from (b)(i).[2 marks]
wavelength increases (so frequency decreases) / light is redshifted
galaxy is moving away from Earth
Allow ECF for MP2 (ie wavelength decreases so moving towards).[2 marks]
A buoy, floating in a vertical tube, generates energy from the movement of water waves on the surface of the sea. When the buoy moves up, a cable turns a generator on the sea bed producing power. When the buoy moves down, the cable is wound in by a mechanism in the generator and no power is produced.
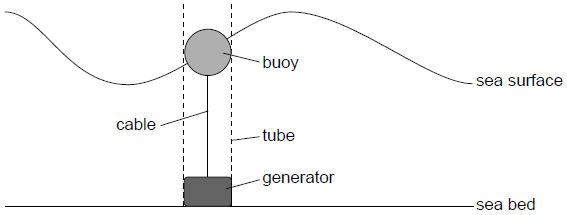
The motion of the buoy can be assumed to be simple harmonic.
Water can be used in other ways to generate energy.
a.
Outline the conditions necessary for simple harmonic motion (SHM) to occur.[2]
A wave of amplitude 4.3 m and wavelength 35 m, moves with a speed of 3.4 m s–1. Calculate the maximum vertical speed of the buoy.[3]
Sketch a graph to show the variation with time of the generator output power. Label the time axis with a suitable scale.
 [2]
[2]
Outline, with reference to energy changes, the operation of a pumped storage hydroelectric system.[2]
The water in a particular pumped storage hydroelectric system falls a vertical distance of 270 m to the turbines. Calculate the speed at which water arrives at the turbines. Assume that there is no energy loss in the system.[2]
The hydroelectric system has four 250 MW generators. Determine the maximum time for which the hydroelectric system can maintain full output when a mass of 1.5 x 1010 kg of water passes through the turbines.[2]
Not all the stored energy can be retrieved because of energy losses in the system. Explain two such losses.
 [2]
[2]
Answer/Explanation
Markscheme
a.
force/acceleration proportional to displacement «from equilibrium position»
and directed towards equilibrium position/point
OR
and directed in opposite direction to the displacement from equilibrium position/point
Do not award marks for stating the defining equation for SHM.
Award [1 max] for a ω–=2x with a and x defined.
frequency of buoy movement \( = \frac{{3.4}}{{35}}\) or 0.097 «Hz»
OR
time period of buoy \( = \frac{{35}}{{3.4}}\) or 10.3 «s» or 10 «s»
v = «\(\frac{{2\pi {x_0}}}{T}\) or \(2\pi f{x_0}\)» \(\ = \frac{{2 \times \pi \times 4.3}}{{10.3}}\) or \(2 \times \pi \times 0.097 \times 4.3\)
2.6 «m s–1»
peaks separated by gaps equal to width of each pulse «shape of peak roughly as shown»
one cycle taking 10 s shown on graph
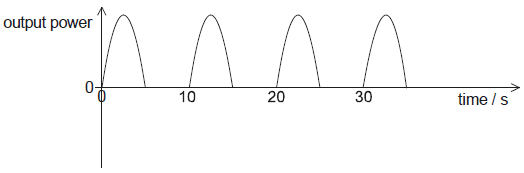
Judge by eye.
Do not accept cos2 or sin2 graph
At least two peaks needed.
Do not allow square waves or asymmetrical shapes.
Allow ECF from (b)(i) value of period if calculated.
PE of water is converted to KE of moving water/turbine to electrical energy «in generator/turbine/dynamo»
idea of pumped storage, ie: pump water back during night/when energy cheap to buy/when energy not in demand/when there is a surplus of energy
specific energy available = «gh =» 9.81 x 270 «= 2650J kg–1»
OR
mgh \( = \frac{1}{2}\)mv2
OR
v2 = 2gh
v = 73 «ms–1»
Do not allow 72 as round from 72.8
total energy = «mgh = 1.5 x 1010 x 9.81 x 270=» 4.0 x 1013 «J»
OR
total energy = «\(\frac{1}{2}m{v^2} = \frac{1}{2} \times 1.5 \times {10^{10}} \times \) (answer (c)(ii))2 =» 4.0 x 1013 «J»
time = «\(\frac{{4.0 \times {{10}^{13}}}}{{4 \times 2.5 \times {{10}^8}}}\)» 11.1h or 4.0 x 104 s
Use of 3.97 x 1013 «J» gives 11 h.
For MP2 the unit must be present.
friction/resistive losses in pipe/fluid resistance/turbulence/turbine or generator «bearings»
OR
sound energy losses from turbine/water in pipe
thermal energy/heat losses in wires/components
water requires kinetic energy to leave system so not all can be transferred
Must see “seat of friction” to award the mark.
Do not allow “friction” bald.