This question is about lasers.
With reference to the light waves emitted by a laser, state what is meant by the terms
(i) monochromatic.
(ii) coherent.
▶️Answer/Explanation
Markscheme
(i) (the waves) all have the same frequency/wavelength;
Do not accept “one colour”.
(ii) (the waves) are all in phase with each other / the phase difference between the waves is constant;
Examiners report
Most candidates knew what was meant by the terms monochromatic and coherent.
This question is about standing waves and organ pipes.
a.An organ pipe of length \(L\) is closed at one end. On the diagrams, draw a representation of the displacement of the air in the pipe when the frequency of the note emitted by the pipe is the
b.(i) State one way in which a standing wave differs from a travelling wave.[1]
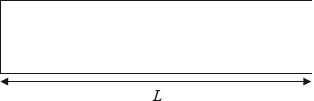
(ii) second harmonic frequency \({f_2}\).
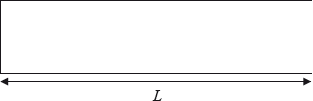 [2]
[2]
d.State, in terms of the boundary conditions of the standing waves that can be formed in the pipe, the reason why the ratio of the higher frequencies of the harmonics to that of the first harmonic must always be an integer number.[1]
▶️Answer/Explanation
Markscheme
a.no energy propagated in a standing wave;
the amplitude of a standing wave is not constant;
points along a standing wave are either in phase or out of phase with each other / OWTTE;
(ii) antinode at open end and node at closed end and one more node along pipe;
(judge by eye)
for \({\lambda _1} = 4L\) and for \({\lambda _2} = \frac{{4L}}{3}\);
\({f_1} = \frac{c}{{4L}}\) and \({f_2} = \frac{{3c}}{{4L}}\);
\(\frac{{{f_1}}}{{{f_2}}} = \frac{1}{3}\);
d.there must always be a node at the closed end and an antinode at the open end / there must always be an integer number of \(\frac{\lambda }{4}\);