IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 6.1 Circular motion
Topic 6 Weightage : 1 %
All Questions for Topic 6.1 – Period, frequency, angular displacement and angular velocity , Centripetal force , Centripetal acceleration
Question
A child stands on a horizontal rotating platform that is moving at constant angular speed. The centripetal force on the child is provided by
A the gravitational force on the child.
B the friction on the child’s feet.
C the tension in the child’s muscles.
D the normal reaction of the platform on the child.
▶️Answer/Explanation
Ans: B
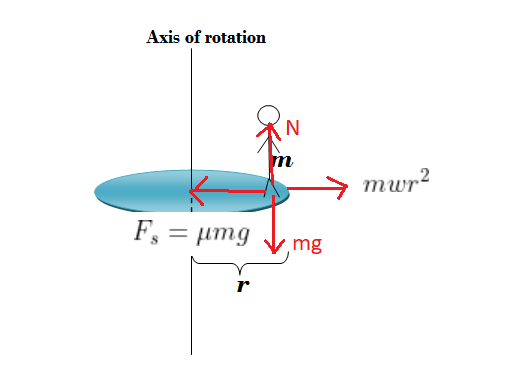
Centripetal force \(\mu mg \) is provides by frictional force . It balances centrifugal force = \(mrw^2\)
Question
An object of mass m moves in a horizontal circle of radius r with a constant speed v. What is the rate at which work is done by the centripetal force?
A. \(\frac{{m{v^3}}}{r}\)
B. \(\frac{{m{v^3}}}{{2\pi r}}\)
C. \(\frac{{m{v^3}}}{{4\pi r}}\)
D. zero
▶️Answer/Explanation
Markscheme
D
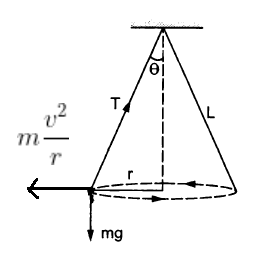
Here you can see centripetal force \(T cos \theta\) which is equal to \(m\frac{v^2}{r}\) is directed towards center and object moves in tenagent to the circle. Hence angle \(\theta \) between force and displacement is \(90^{\circ}\).
Now work done by a force is given by \( F s cos \theta\)
\(= F s cos 90^{\circ} = 0\) as \( cos 90^{\circ}\) = 0
Question
A small ball of weight W is attached to a string and moves in a vertical circle of radius R.
What is the smallest kinetic energy of the ball at position X for the ball to maintain the circular motion with radius R?
A. \(\frac{{W\,R}}{2}\)
B. W R
C. 2 W R
D. \(\frac{{5W\,R}}{2}\)
▶️Answer/Explanation
Markscheme
D
This is related to motion in vertical circle
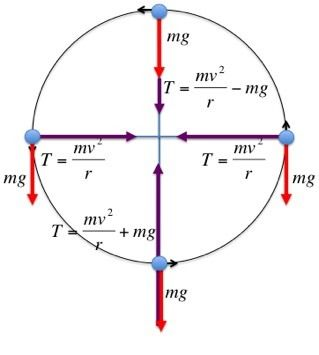
At Top:
Minimum Velocity required to complete the circle is
\(\frac{mv^2_{Top}}{r}-mg=0\)
or \(\frac{mv^2_{Top}}{2}=\frac{mgR}{2}\) ..1
Now consider point X and at Top. Total energy is conserved that is
\(\frac{1}{2}mv^2_x = mg(2R)+\frac{1}{2}mv^2_{Top}\) ..2
Here we have 2R as height from bottom to Top is 2R (Diameter)
From equation 1 and 2 , we get
kinetic Energy at Point X = \(\frac{1}{2}mv^2_x = \frac{1}{2}mgR+2mgR= \frac{5}{2}mgR=\frac{5}{2}WR\) as W=mg =Weight
Question
A car travels in a horizontal circle at constant speed. At any instant the resultant horizontal force acting on the car is
A. zero.
B. in the direction of travel of the car.
C. directed out from the centre of the circle.
D. directed towards the centre of the circle.
▶️Answer/Explanation
Markscheme
D
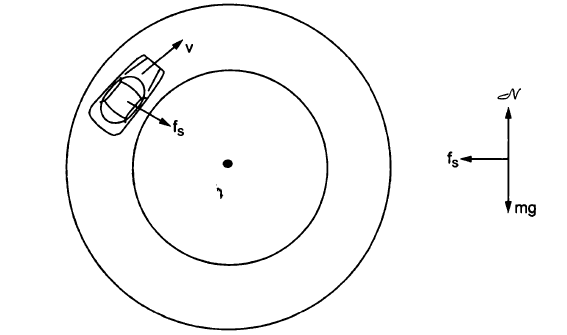
The external forces acting on the vehicle are
(i) weight \(mg\)
(ii) Normal contact force \(N\) and
(iii) friction \(f_s\)
If the road is horizontal, the normal force \(N\) and weight \(mg\) balanced out . The only horizontal force that can act towards the centre is the friction \(f_s\).
Question
Particle P is moving with uniform speed in a horizontal circle. Which of the following shows the correct directions of the acceleration a and the velocity v of P at the position shown?
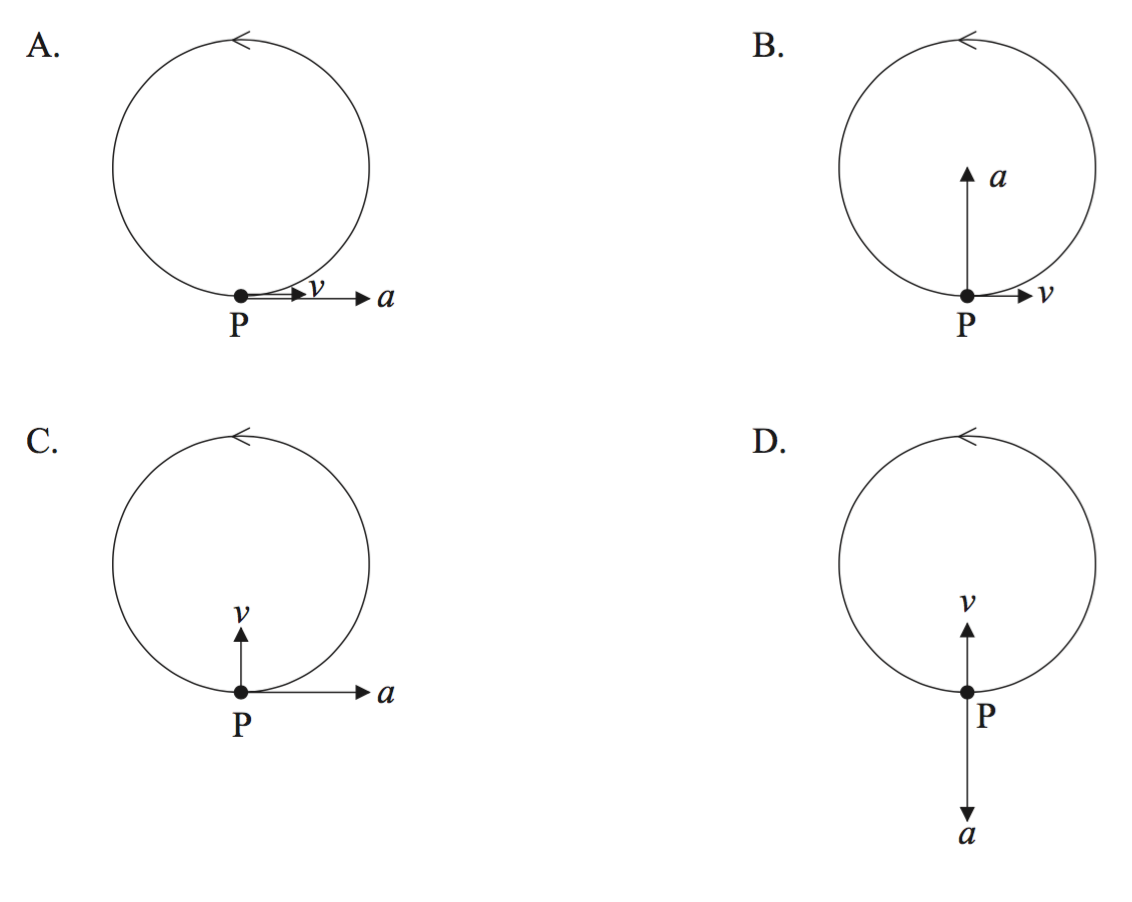
▶️Answer/Explanation
Markscheme
B
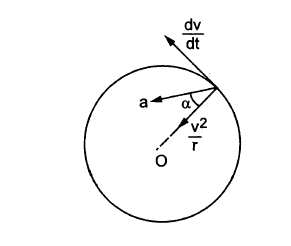
\(a_r =-w^2r=-\frac{v^2}{r}\)
and
\(a_t=\frac{dv}{dt}\)
\(a=\sqrt{a_r^2+a_t^2}\)
\(=\sqrt{(\frac{v^2}{r})^2+(w^2r)^2}\)
\(tan \alpha =\frac{\frac{dv}{dt}}{\frac{v^2}{r}}\)
for uniform speed in a horizontal circle \(\frac{dv}{dt}=0 \; , tan \alpha = 0\)
\(\therefore \alpha = 0\)
Question
A particle of mass m is moving with constant speed v in uniform circular motion. What is the total work done by the centripetal force during one revolution?
A. Zero
B. \(\frac{{m{v^2}}}{2}\)
C. mv2
D. 2πmv2
▶️Answer/Explanation
Markscheme
A

Here you can see centripetal force \(T cos \theta\) which is equal to \(m\frac{v^2}{r}\) is directed towards center and object moves in tenagent to the circle. Hence angle \(\theta \) between force and displacement is \(90^{\circ}\).
Now work done by a force is given by \( F s cos \theta\)
\(= F s cos 90^{\circ} = 0\) as \( cos 90^{\circ}\) = 0