IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 6.1 Circular motion
Topic 6 Weightage : 1 %
All Questions for Topic 6.1 – Period, frequency, angular displacement and angular velocity , Centripetal force , Centripetal acceleration
The gravitational potential due to the Sun at its surface is –1.9 x 1011 J kg–1. The following data are available.
| Mass of Earth | = 6.0 x 1024 kg |
| Distance from Earth to Sun | = 1.5 x 1011 m |
| Radius of Sun | = 7.0 x 108 m |
a.
Outline why the gravitational potential is negative.[2]
The gravitational potential due to the Sun at a distance r from its centre is VS. Show that
rVS = constant.[1]
Calculate the gravitational potential energy of the Earth in its orbit around the Sun. Give your answer to an appropriate number of significant figures.[2]
Calculate the total energy of the Earth in its orbit.[2]
An asteroid strikes the Earth and causes the orbital speed of the Earth to suddenly decrease. Suggest the ways in which the orbit of the Earth will change.[2]
Outline, in terms of the force acting on it, why the Earth remains in a circular orbit around the Sun.[2]
▶️Answer/Explanation
Markscheme
a.
potential is defined to be zero at infinity
so a positive amount of work needs to be supplied for a mass to reach infinity
VS = \( – \frac{{GM}}{r}\) so r x VS «= –GM» = constant because G and M are constants
GM = 1.33 x 1020 «J m kg–1»
GPE at Earth orbit «= –\(\frac{{1.33 \times {{10}^{20}} \times 6.0 \times {{10}^{24}}}}{{1.5 \times {{10}^{11}}}}\)» = «–» 5.3 x 1033 «J»
Award [1 max] unless answer is to 2 sf.
Ignore addition of Sun radius to radius of Earth orbit.
ALTERNATIVE 1
work leading to statement that kinetic energy \(\frac{{GMm}}{{2r}}\), AND kinetic energy evaluated to be «+» 2.7 x 1033 «J»
energy «= PE + KE = answer to (b)(ii) + 2.7 x 1033» = «–» 2.7 x 1033 «J»
ALTERNATIVE 2
statement that kinetic energy is \( = – \frac{1}{2}\) gravitational potential energy in orbit
so energy «\( = \frac{{{\text{answer to (b)(ii)}}}}{2}\)» = «–» 2.7 x 1033 «J»
Various approaches possible.
«KE will initially decrease so» total energy decreases
OR
«KE will initially decrease so» total energy becomes more negative
Earth moves closer to Sun
new orbit with greater speed «but lower total energy»
changes ellipticity of orbit
centripetal force is required
and is provided by gravitational force between Earth and Sun
Award [1 max] for statement that there is a “centripetal force of gravity” without further qualification.
Question
The Rotor is an amusement park ride that can be modelled as a vertical cylinder of inner radius R rotating about its axis. When the cylinder rotates sufficiently fast, the floor drops out and the passengers stay motionless against the inner surface of the cylinder. The diagram shows a person taking the Rotor ride. The floor of the Rotor has been lowered away from the person
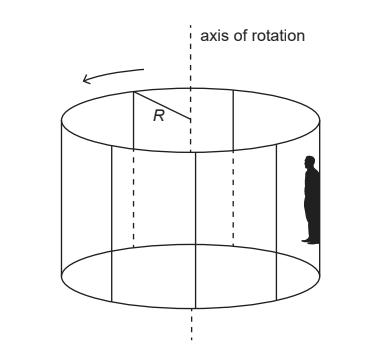
(a) Draw and label the free-body diagram for the person. [2]

(b) The person must not slide down the wall. Show that the minimum angular velocity ω of the cylinder for this situation is
ω =
where ω is the coefficient of static friction between the person and the cylinder. [2]
(c) The coefficient of static friction between the person and the cylinder is 0.40. The radius of the cylinder is 3.5 m. The cylinder makes 28 revolutions per minute. Deduce whether the person will slide down the inner surface of the cylinder. [3]
▶️Answer/Explanation
Ans.
a
arrow downwards labelled weight/W/mg and arrow upwards labelled friction/F
arrow horizontally to the left labelled «normal» reaction/N

b
See F N = μ AND N mR = ω2
«substituting for N» ω2m R= mg
c
ALTERNATIVE 1
minimum required angular velocity « = \(\sqrt{\frac{9.81}{0.40\times 3.5}}\) » = 2.6 «rad s-1»
actual angular velocity « \(\frac{2\pi }{(\frac{60}{28})}\) 2.9 « = 2.9 «rad s-1»
actual angular velocity is greater than the minimum, so the person does not slide ✓
ALTERNATIVE 2
minimum friction force = mg = «9.81m »
actual friction force « = μmRω2 = 0.40 m ×3.5 \((2\pi \frac{28}{60})^2\) » = 12.0m
actual friction force is greater than the minimum frictional force so the person does not slide