IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 6.1 – Circular motion
Topic 6 Weightage : 4 %
All Questions for Topic 6.1 – Period, frequency, angular displacement and angular velocity , Centripetal force , Centripetal acceleration
Question
A child stands on a horizontal rotating platform that is moving at constant angular speed. The centripetal force on the child is provided by
A the gravitational force on the child.
B the friction on the child’s feet.
C the tension in the child’s muscles.
D the normal reaction of the platform on the child.
▶️Answer/Explanation
Ans: B
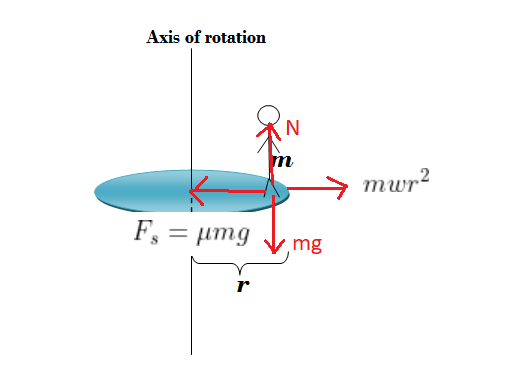
Centripetal force \(\mu mg \) is provides by frictional force . It balances centrifugal force = \(mrw^2\)
Question
A mass at the end of a string is swung in a horizontal circle at increasing speed until the string breaks.
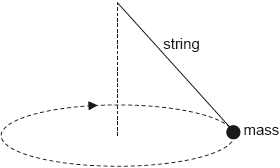
The subsequent path taken by the mass is a
A. line along a radius of the circle.
B. horizontal circle.
C. curve in a horizontal plane.
D. curve in a vertical plane.
▶️Answer/Explanation
Markscheme
D
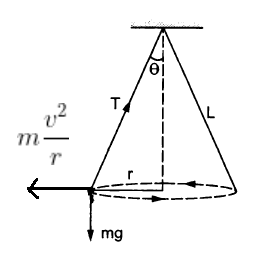
We have \(Tsin\theta = mg\) and
\(Tcos \theta = m\frac{v^2}{r}\)
When string break , only force acting is \(mg\) and hence body will move under influence of this gravitation force .

Question
An object of mass m at the end of a string of length r moves in a vertical circle at a constant angular speed ω.
What is the tension in the string when the object is at the bottom of the circle?
A. m(ω2r + g)
B. m(ω2r – g)
C. mg(ω2r + 1)
D. mg(ω2r – 1)
▶️Answer/Explanation
Markscheme
A
As the bob moves in a vertical circle with centre at 0, the radial acceleration is \(\frac{v^2}{r} =w^2r\) towards 0. Taking the components along this radius and applying Newton’s second law, we get
\(T-mgcos\theta=mw^2r\)
or
\(T =mw^2r +mgcos\theta\)
when \( \theta =0 \;cos\theta = 1\)
\(T =mw^2r +mg =m(w^2r+g)\)
Question
An object of constant mass is tied to the end of a rope of length l and made to move in a horizontal circle. The speed of the object is increased until the rope breaks at speed v. The length of the rope is then changed. At what other combination of rope length and speed will the rope break?
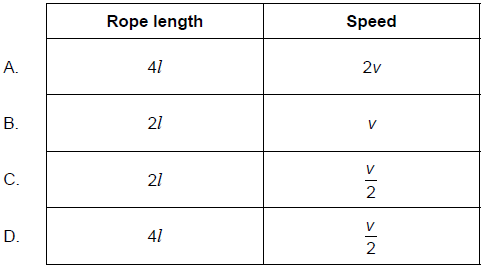
▶️Answer/Explanation
Markscheme
A

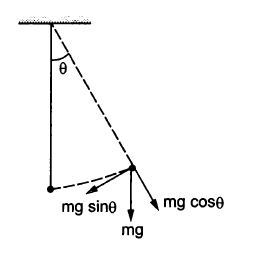
We have \(Tsin\theta = mg\) and
\(Tcos \theta = m\frac{v^2}{r}\) —(1)
Also
\(tan \theta = \frac{r}{L}\)
\(r =L tan\theta\)
putting this in equation (1) we get
\(T= \frac{mv^2}{ltan \theta \times cos \theta}\)
\(=\frac{mv^2}{lsin\theta}\)
Hence when \( l \) increased so \( v \) will have to increase to break rope again i.e. get same T
if \(l{}’= 4l \) then \(v{}’ = 2v \) to get same T