IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 7.1 Discrete energy and radioactivity
Topic 7 Weightage : 3 %
All Questions for Topic 7.1 – Discrete energy and discrete energy levels , Transitions between energy levels , Radioactive decay , Fundamental forces and their properties , Alpha particles, beta particles and gamma rays , Half-life , Absorption characteristics of decay particles , Isotopes , Background radiation
Question
A simple model of an atom has three energy levels. The differences between adjacent energy levels are shown below.
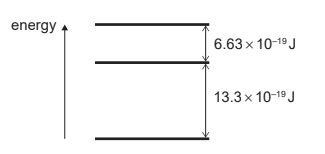
What are the two smallest frequencies in the emission spectrum of this atom?
A. 0.5 ×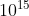 
Hz and 1.0 × 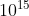Hz
B. 0.5 × 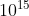Hz and 1.5 × 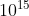Hz
C. 1.0 × 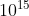Hz and 2.0 × 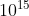Hz
D. 1.0 × 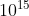Hz and 3.0 × 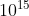Hz
▶️Answer/Explanation
Ans: C
\(6.63 \times 10^{-19}J \)and
\(13.3 \times 10^{-19}J\) are two smallest energy jump
Hence for \(6.63 \times 10^{-19}J\)
\(\nu =\frac{6.63 \times 10^{-19}}{h}\)
Now \( h = 6.6 \times 10^{-34}\)
\(\therefore\)
\(\nu =\frac{6.63 \times 10^{-19}}{h} = \frac{6.63 \times 10^{-19}}{6.6 \times 10^{-34}}= 1.0 \times 10^{15}\)
for \( 13.3 \times 10^{-19}J\)
\(\nu =\frac{13.3 \times 10^{-19}}{6.6 \times 10^{-34}} =2.0 \times 10^{15}\)
Hence C is answer
Question
Which of the following leads to a paradigm shift?
A. Multi-loop circuits
B. Standing waves
C. Total internal reflection
D. Atomic spectra
▶️Answer/Explanation
Markscheme
D
Atomic Spectroscopy is used as a tool for studying the structures of atoms and molecules. The large number of wavelengths emitted by these systems makes it possible to investigate their structures in detail, including the electron configurations of ground and various excited states.
Spectroscopy also provides a precise analytical method for finding the constituents in material having unknown chemical composition. In a typical spectroscopic analysis, a concentration of a few parts per million of a trace element in a material can be detected through its emission spectrum.
In astronomy the study of the spectral emission lines of distant galaxies led to the discovery that the universe is expanding rapidly and isotropically (independent of direction). The finding was based on the observation of a Doppler shift of spectral lines. The Doppler shift is an effect that occurs when a source of radiation such as a star moves relative to an observer. The frequency will be shifted in much the same way that an observer on a moving train hears a shift in the frequency of the pitch of a ringing bell at a railroad crossing. The pitch of the bell sounds higher if the train is approaching the crossing and lower if it is moving away. Similarly, light frequencies will be Doppler-shifted up or down depending on whether the light source is approaching or receding from the observer. During the 1920s, the American astronomer Edwin Hubble identified the diffuse elliptical and spiral objects that had been observed as galaxies. He went on to discover and measure a roughly linear relationship between the distance of these galaxies from Earth and their Doppler shift. In any direction one looks, the farther the galaxy appears, the faster it is receding from Earth.
Spectroscopic evidence that the universe was expanding was followed by the discovery in 1965 of a low level of isotropic microwave radiation by the American scientists Arno A. Penzias and Robert W. Wilson. The measured spectrum is identical to the radiation distribution expected from a blackbody, a surface that can absorb all the radiation incident on it. This radiation, which is currently at a temperature of 2.73 kelvin (K), is identified as a relic of the big bang that marks the birth of the universe and the beginning of its rapid expansion
Question
A pure sample of nuclide A and a pure sample of nuclide B have the same activity at time t = 0. Nuclide A has a half-life of T, nuclide B has a half-life of 2T.
What is \(\frac{{{\text{activity of A}}}}{{{\text{activity of B}}}}\) when t = 4T?
A. 4
B. 2
C. \(\frac{1}{2}\)
D. \(\frac{1}{4}\)
▶️Answer/Explanation
Markscheme
D
We have activity formula as
\(A_t=\frac{A_0}{2^{\frac{t}{t_{\frac{1}{2}}}}}\)
Given that at \(t=0\) Activity of A = Activity of B = \(A_0\)
Hence
\(A_{At} =\frac{A_0}{2^{\frac{t}{t_{\frac{1}{2}(A)}}}}\)
and
\(A_{Bt} =\frac{A_0}{2^{\frac{t}{t_{\frac{1}{2}(B)}}}}\)
\(t_{\frac{1}{2}(A)} = T\)
\(t_{\frac{1}{2}(B)} = 2T\)
and \(t= 4T\)
Putting the value in above equations , we get
\(A_{At} =\frac{A_0}{2^{\frac{4T}{T}}}=\frac{A_0}{2^4}\)
\(A_{Bt} =\frac{A_0}{2^{\frac{4T}{2T}}}=\frac{A_0}{2^2}\)
Hence
\(\frac{A_{At}}{A_{Bt}} =\frac{\frac{A_0}{2^4}}{\frac{A_0}{2^2}}=\frac{2^2}{2^4}=\frac{1}{4}\)
Question
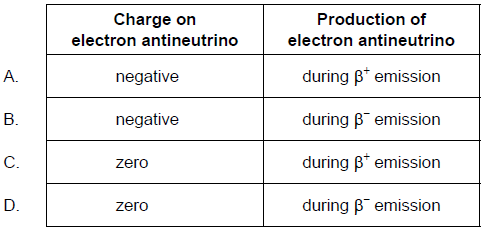
What is the charge on an electron antineutrino and during what process is an electron antineutrino produced?
▶️Answer/Explanation
Markscheme
D
When a neutron is converted into a proton, an electron and a new particle named antineutrino are created and emitted from the nucleus,
\(n\rightarrow p+e+\bar{\nu}\)
The antineutrino is denoted by the symbol \(\bar{\nu}\) . It is supposed to have zero rest mass like photon, is chargeless and has spin quantum number ± 1/2.
The electron emitted from the nucleus is called a beta particle and is denoted by the symbol \(\beta^{-}\)
Question
Which of the following lists the particles emitted during radioactive decay in order of increasing ionizing power?
A. γ, β, α
B. β, α, γ
C. α, γ, β
D. α, β, γ
▶️Answer/Explanation
Markscheme
A
When the radiations interact with the atoms, the atoms lose electrons and thus are ionised. The greater the ionising power of the radiation, more is the process of ionising. As a result, more damage is caused to the atoms. The ionising power is directly proportional to the mass of the particle.
The particles are a helium nucleus and the most heavy of the three so hits more particles on its travels so can’t travel as far but ionizes more along its way.
The particles are highly energetic electrons that, being smaller than particles, can travel further but ionize less.
The particles are highly energetic photons that rarely interact with matter so can travel very far and ionize the least.
Question
Some of the energy levels for a hydrogen atom are shown in the diagram.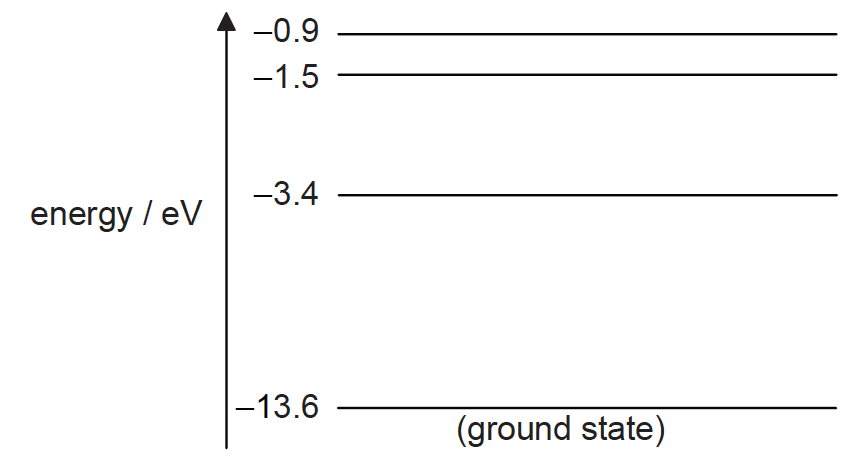
The table shows four photons with their corresponding energies.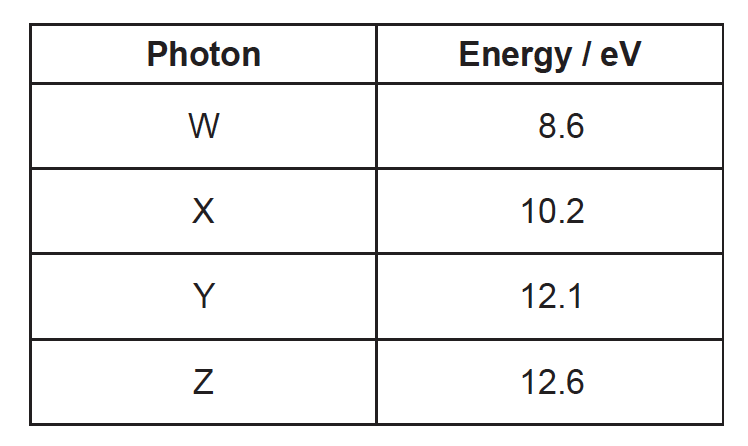
Each photon is incident on a hydrogen atom in its ground state. Which photons could be absorbed by the atom?
A. W only
B. X and Y only
C. Y and Z only
D. X, Y and Z only
▶️Answer/Explanation
Markscheme
B
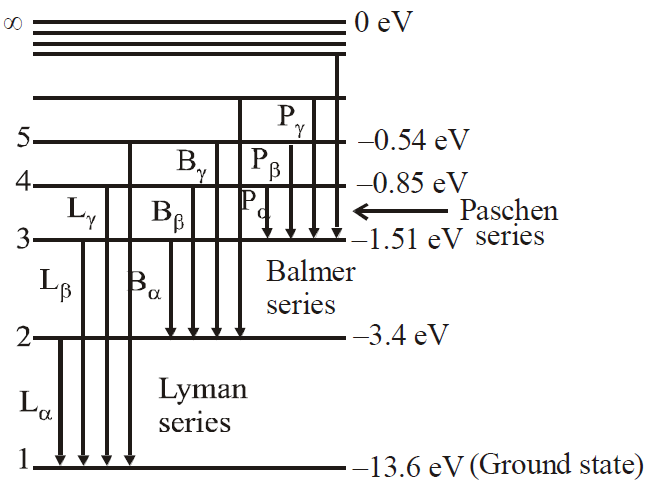
\(E_3-E_1=13.6-1.5 =12.1\)
\(E_2-E_1 =13.6-3.4=10.2\)
\(E_4-E_2 =3.4-0.9= 2.5\)
\(E_4-E_3= =1.5-0.9 =0.6\)
\(E_3-E_2=3.4-1.5 =1.9 \)