IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 7.1 Discrete energy and radioactivity
Topic 7 Weightage : 3 %
All Questions for Topic 7.1 – Discrete energy and discrete energy levels , Transitions between energy levels , Radioactive decay , Fundamental forces and their properties , Alpha particles, beta particles and gamma rays , Half-life , Absorption characteristics of decay particles , Isotopes , Background radiation
Question
A sample of waste produced by the reactor contains 1.0 kg of strontium-94 (Sr-94). Sr-94 is radioactive and undergoes beta-minus (β–) decay into a daughter nuclide X.
The reaction for this decay is
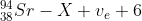
(i) Write down the proton number of nuclide X. [1]
The graph shows the variation with time of the mass of Sr-94 remaining in the sample.
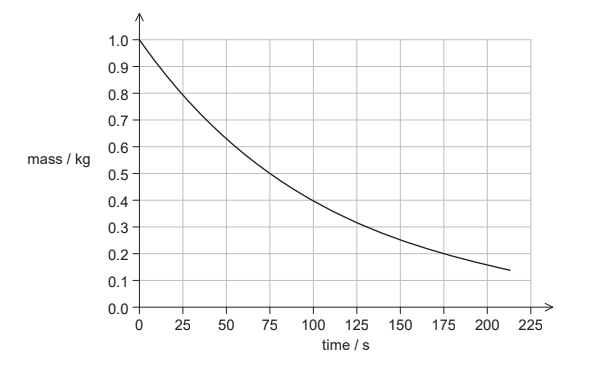
(ii) State the half-life of Sr-94. [1]
(iii) Calculate the mass of Sr-94 remaining in the sample after 10 minutes. [2]
▶️Answer/Explanation
Ans
i 39
ii 75 «s»
iii
ALTERNATIVE 1
10 min = 8 1/2 t mass remaining = 1.0 × \((\frac{1}{2})^8\) = 3.9 × 10-3 «kg»
ALTERNATIVE 2
decay constant = «\(\frac{In2}{75}\) = » 9.24 ×10-3 «s-1» mass remaining 10 × e -9.24 ×10-3×600 = 3.9 × 10-3«kg»
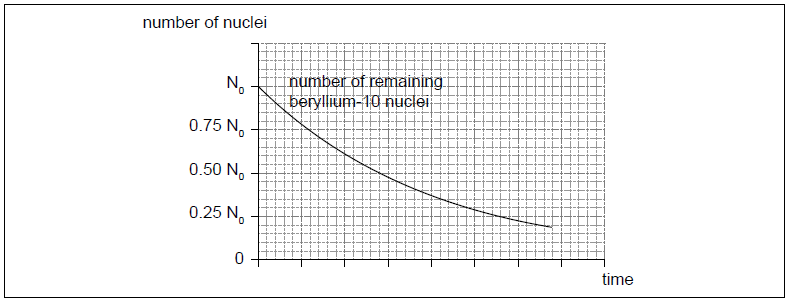
The radioactive nuclide beryllium-10 (Be-10) undergoes beta minus (β–) decay to form a stable boron (B) nuclide.
The initial number of nuclei in a pure sample of beryllium-10 is N0. The graph shows how the number of remaining beryllium nuclei in the sample varies with time.
An ice sample is moved to a laboratory for analysis. The temperature of the sample is –20 °C.
a.
Identify the missing information for this decay.
 [2]
[2]
Beryllium-10 is used to investigate ice samples from Antarctica. A sample of ice initially contains 7.6 × 1011 atoms of beryllium-10. The present activity of the sample is 8.0 × 10−3 Bq.
Determine, in years, the age of the sample.[3]
The temperature in the laboratory is higher than the temperature of the ice sample. Describe one other energy transfer that occurs between the ice sample and the laboratory.[2]
▶️Answer/Explanation
Markscheme
a.
\(_{{\mkern 1mu} {\mkern 1mu} 4}^{10}{\text{Be}} \to _{{\mkern 1mu} {\mkern 1mu} 5}^{10}{\text{B}} + _{ – 1}^{\,\,\,0}{\text{e}} + {\overline {\text{V}} _{\text{e}}}\)
antineutrino AND charge AND mass number of electron \(_{ – 1}^{\,\,\,0}{\text{e}}\), \(\overline {\text{V}} \)
conservation of mass number AND charge \(_{\,\,5}^{10}{\text{B}}\), \(_{{\mkern 1mu} {\mkern 1mu} 4}^{10}{\text{Be}}\)
Do not accept V.
Accept \({\bar V}\) without subscript e.[2 marks]
λ «= \(\frac{{\ln 2}}{{1.4 \times {{10}^6}}}\)» = 4.95 × 10–7 «y–1»
rearranging of A = λN0e–λt to give –λt = ln \(\frac{{8.0 \times {{10}^{-3}} \times 365 \times 24 \times 60 \times 60}}{{4.95 \times {{10}^{-7}} \times 7.6 \times {{10}^{11}}}}\) «= –0.400»
t = \(\frac{{ – 0.400}}{{ – 4.95 \times {{10}^{ – 7}}}} = 8.1 \times {10^5}\) «y»
Allow ECF from MP1[3 marks]
from the laboratory to the sample
conduction – contact between ice and lab surface.
OR
convection – movement of air currents
Must clearly see direction of energy transfer for MP1.
Must see more than just words “conduction” or “convection” for MP2.[2 marks]