IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 3.1 – Thermal Concepts
Topic 3 Weightage : 3 %
All Questions for Topic 3.1 –Molecular theory of solids, liquids and gases , Temperature and absolute temperature , Internal energy , Specific heat capacity , Phase change , Specific latent heat
Question
A sample of vegetable oil, initially in the liquid state, is placed in a freezer that transfers thermal energy from the sample at a constant rate. The graph shows how temperature T of the sample varies with time t.
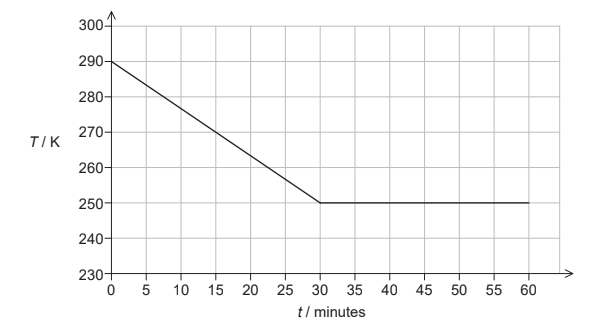
The following data are available.
Mass of the sample = 0.32 kg
Specific latent heat of fusion of the oil = 130 kJ kg–1
Rate of thermal energy transfer = 15 W
(a ) (i) Calculate the thermal energy transferred from the sample during the first 30 minutes. [1]
(ii) Estimate the specific heat capacity of the oil in its liquid phase. State an appropriate unit for your answer. [2]
(b) The sample begins to freeze during the thermal energy transfer. Explain, in terms of the molecular model of matter, why the temperature of the sample remains constant during freezing. [3]
(c) Calculate the mass of the oil that remains unfrozen after 60 minutes. [2]
▶️Answer/Explanation
Ans:
a i « » 15 × 30 × 60 » = 27000 «J»
a ii 27 × 10 3 = 0.32 × c × (290 250) OR 2100 J kg-1 K-1 OR J kg-1 0C-1
b
«intermolecular» bonds are formed during freezing
bond-forming process releases energy
OR
«intermolecular» PE decreases «and the difference is transferred as heat»
«average random» KE of the molecules does not decrease/change
temperature is related to «average» KE of the molecules «hence unchanged»
c
mass of frozen oil « = \(\frac{27\times 10^3}{130\times 10^3}\) » 0.21 «kg»
unfrozen mass «= 0.32 – 0.21»= 0.11 «kg »
A closed box of fixed volume 0.15 m3 contains 3.0 mol of an ideal monatomic gas. The temperature of the gas is 290 K.
When the gas is supplied with 0.86 kJ of energy, its temperature increases by 23 K. The specific heat capacity of the gas is 3.1 kJ kg–1 K–1.
Determine, in kJ, the total kinetic energy of the particles of the gas.
▶️Answer/Explanation
Markscheme
ALTERNATIVE 1
average kinetic energy = \(\frac{3}{2}\)1.38 × 10–23 × 313 = 6.5 × 10–21 «J»
number of particles = 3.0 × 6.02 × 1023 = 1.8 × 1024
total kinetic energy = 1.8 × 1024 × 6.5 × 10–21 = 12 «kJ»
ALTERNATIVE 2
ideal gas so U = KE
KE = \(\frac{3}{2}\)8.31 × 131 × 3
total kinetic energy = 12 «kJ»
[3 marks]