IB Physics Unit 1. Measurements and uncertainties- 1.1 Measurements in physics: Study Notes

IB DP PhysicsIB DP MathsIB DP ChemistryIB DP Biology

IBDP Physics: Study Notes- All Chapters

1.1 Measurements in physics

Essential Idea:
Since 1948, the Système International d’Unités (SI) has been used as the preferred language of science and technology across the globe and reflects current best measurement practice

Understandings:

  • Fundamental and derived SI units
  • Scientific notation and metric multipliers
  • Significant figures
  • Orders of magnitude
  • Estimation

Applications and Skills:

  • Using SI units in the correct format for all required measurements, final answers to calculations and presentation of raw and processed data
  • Using scientific notation and metric multipliers
  • Quoting and comparing ratios, values and approximations to the nearest order of magnitude Estimating quantities to an appropriate number of significant figures

PHYSICAL WORLD

WHAT IS SCIENCE?

Science refers to a system of acquiring knowledge. This system uses observation and experimentation to describe and explain natural phenomena. The term science also refers to the organized body of knowledge that people have gained using that system. Less formally, the word science often describes any systematic field of study or the knowledge gained from it.

 Purpose of science is to produce useful models of reality. Most scientific investigations use some form of the scientific method.

Scientific method is a logical and rational order of steps by which scientists come to conclusions about the world around them. The Scientific method helps to organize thoughts and procedures so that scientists can be confident in the answers they find. Scientists use observations, hypotheses, and deductions to make these conclusions.

 Science as defined above, is sometimes called pure science to differentiate it from applied science, which is the application of research to human needs. Fields of science are commonly divided into two major categories.

  • Natural science : The science in which we study about the natural world. Natural science includes physics, chemistry, biology, etc.  
  • Social science : It is the systematic study of human behavior and society.  

WHAT IS PHYSICS?

The word physics originates from a Greek word which means nature. Physics is the branch of science that deals with the study of basic laws of nature and their manifestation of various natural phenomena.

 There are two main thrusts in physics :

  • Unification : In physics, attempt is made to explain various physical phenomena in terms of just few concepts and laws. Attempts are being made to unify fundamental forces of nature in the pursuit of unification.
  • Reductionism : Another attempt made in physics is to explain a macroscopic system in terms of its microscopic constituents. This pursuit is called reductionism.

 Keep in memory

  • Information received through the senses is called observation.
  • An idea that may explain a number of observations is called hypothesis.
  • A hypothesis that has been tested many times is called scientific theory.
  • A scientific theory that has been tested and has always proved true is called scientific law.

SCOPE AND EXCITEMENT OF PHYSICS

The scope of physics is very vast. It covers a tremendous range of magnitude of physical quantities like length, mass, time, energy, etc. Basically, there are two domains of interest : macroscopic and microscopic. The macroscopic domain includes phenomena at the laboratory, terrestrial and astronomical scales. The microscopic domain includes atomic, molecular and nuclear phenomena.

 Classical physics deals mainly with macroscopic phenomena consisting of the study of heat, light, electricity, magnetism, optics, acoustics, and mechanics. Since the turn of the 20th century, the study of quantum mechanics and relativity has become more important. Today, physics is often divided into branches such as nuclear physics, particle physics, quantum physics, theoretical physics, and solid-state physics. The study of the planets, stars, and their interactions is known as astrophysics, the physics of the Earth is called geophysics, and the study of the physical laws relating to living organisms is called biophysics.

 Physics is exciting in many ways. Application and exploitation of physical laws to make useful devices is the most interesting and exciting part and requires great ingenuity and persistence of effort.

PHYSICS, TECHNOLOGY AND SOCIETY

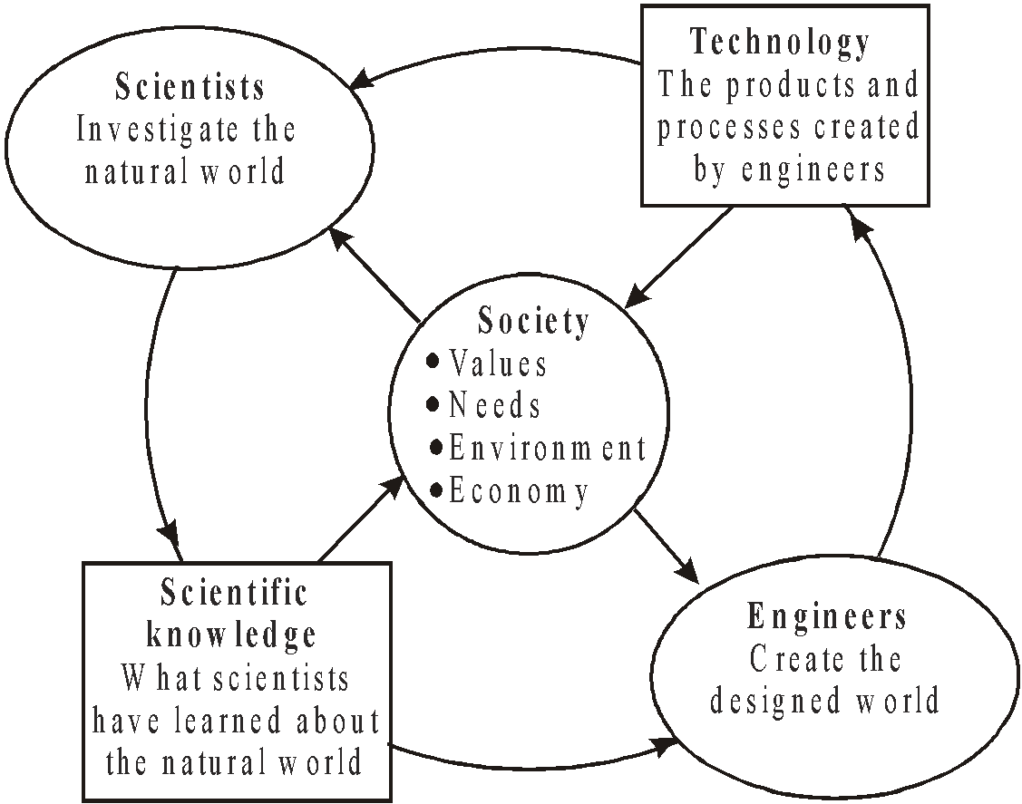
Physics generates new technologies and these technologies have made our lives comfortable and materially prosperous. We hear terms like science, engineering , technology all in same context though they are not exactly same.

 

SCIENCE

  • A body of knowledge
  • Seeks to describe and understand the natural world and its physical properties
  • Scientific knowledge can be used to make predictions
  • Science uses a process–the scientific method–to generate knowledge

ENGINEERING

  • Design under constraint
  • Seeks solutions for societal problems and needs
  • Aims to produce the best solution from given resources and constraints
  • Engineering uses a process–the engineering design process–to produce solutions and technologies

TECHNOLOGY

  • The body of knowledge, processes and artifacts that result from engineering
  • Almost everything made by humans to solve a need is a technology
  • Examples of technology include pencils, shoes, cell phones, and processes to treat water
In the real world, these disciplines are closely connected. Scientists often use technologies created by engineers to conduct their research. In turn, engineers often use knowledge developed by scientists to inform the design of the technologies they create.

LINK BETWEEN TECHNOLOGY AND PHYSICS

 

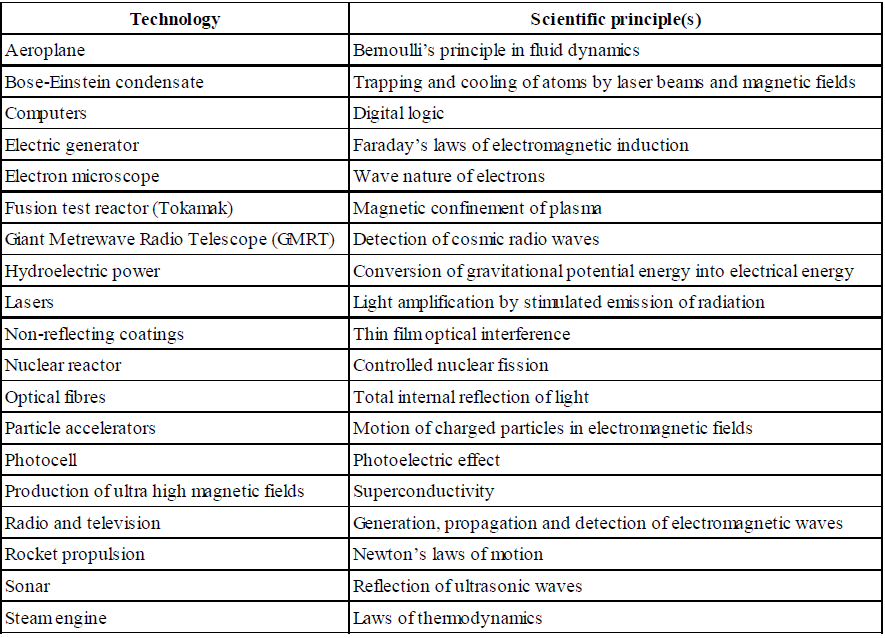
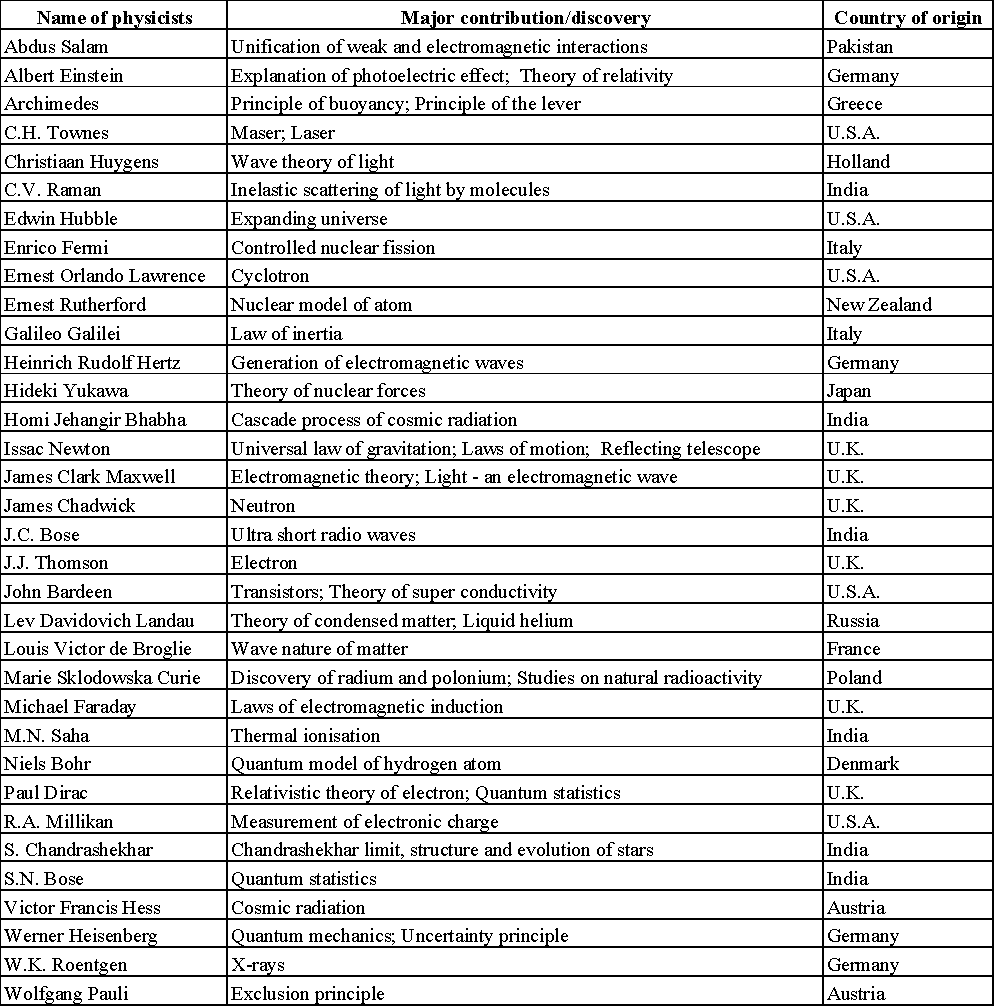
Some physicists from different countries of the world and their major contributions
 

DOES IMAGINATION PLAY ANY ROLE IN PHYSICS?

Yes, imagination has played an important role in the development of physics. Huygen’s principle, Bohr’s theory, Maxwell equations, Heisenberg’s uncertainty principle, etc. were the imaginations of the scientists which successfully explained the various natural phenomena.

HOW IS SCIENCE DIFFERENT FROM TECHNOLOGY?

Science is the study of natural laws while technology is the practical application of these laws to the daily life problems.

FUNDAMENTAL FORCES IN NATURE

We come across several forces in our day-to-day lives eg., frictional force, muscular force, forces exerted by springs and strings etc. These forces actually arise from four fundamental forces of nature.
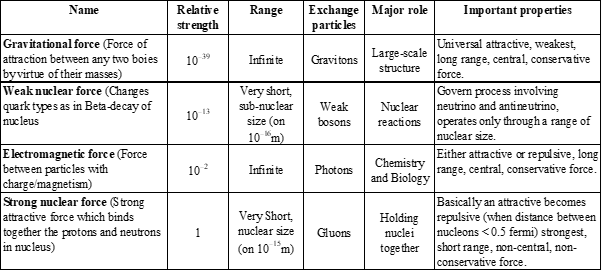
Following are the four fundamental forces in nature.
  • Gravitational force
  • Weak nuclear force
  • Electromagnetic force
  • Strong nuclear force
Among these forces gravitational force is the weakest and strong nuclear force is the strongest force in nature.

FUNDAMENTAL FORCES OF NATURE

Physicists are trying to derive a unified theory that would describe all the forces in nature as a single fundamental law. So far, they have succeeded in producing a unified description of the weak and electromagnetic forces, but a deeper understanding of the strong and gravitational forces has not yet been achieved.
  • Theories that postulate the unification of the strong, weak, and electromagnetic forces are called Grand Unified Theories (often known by the acronym GUTs).
  • Theories that add gravity to the mix and try to unify all four fundamental forces into a single force are called Super Unified Theories.
  • Theory that describes the unified electromagnetic and weak interactions is called the Standard Electroweak Theory, or sometimes just the Standard Model.

PROGRESS IN UNIFICATION OF DIFFERENT FORCES/DOMAINS IN NATURE

test

WHAT IS ELECTROMAGNETIC FORCE?

It is the force due to interaction between two moving charges. It is caused by exchange of photons (γ) between two charged particles.

NATURE OF PHYSICAL LAWS

A physical law, scientific law, or a law of nature is a scientific generalization based on empirical observations of physical behavior. Empirical laws are typically conclusions based on repeated scientific experiments and simple observations over many years, and which have become accepted universally within the scientific community. The production of a summary description of nature in the form of such laws is a fundamental aim of science.

 

Physical laws are distinguished from scientific theories by their simplicity. Scientific theories are generally more complex than laws. They have many component parts, and are more likely to be changed as the body of available experimental data and analysis develops. This is because a physical law is a summary observation of strictly empirical matters, whereas a theory is a model that accounts for the observation, explains it, relates it to other observations, and makes testable predictions based upon it. Simply stated, while a law notes that something happens, a theory explains why and how something happens.

UNITS AND MEASUREMENTS

PHYSICAL QUANTITY

All the quantities in terms of which laws of physics are described and which can be measured directly or indirectly are called physical quantities. For example mass, length, time, speed, force etc.

TYPES OF PHYSICAL QUANTITY

  1. Fundamental quantities : The physical quantities which do not depend upon other physical quantities are called fundamental or base physical quantities. e.g. mass, length, time temperature electric current, luminous intensity and amount of substance.
  2. Derived quantities : The physical quantities which depend on fundamental quantities are called derived quantities
    e.g. speed, acceleration, force, etc.

UNIT

The process of measurement is a comparison process.
Unit is the standard quantity used for comparison.
The chosen standard for measurement of a physical quantity, which has the same nature as that of the quantity is called the unit of that quantity.
Choice of a unit (Characteristics of a unit):
  • It should be suitable in size (suitable to use)
  • It should be accurately defined (so that everybody understands the unit in same way)
  • It should be easily reproducible.
  • It should not change with time.
  • It should not change with change in physical conditions i.e., temperature, pressure, moisture etc.
  • It should be universally acceptable.
Every measured quantity (its magnitude) comprises of a number and a unit. Ex: In the measurement of time, say
If Q is the magnitude of the quantity (which does not depend on the selection of unit) then
Q = n u = n1 u1 = n2 u2 ⇒
Where u1 and u2 are the units and n1 and n2 are the numerical values in two different system of units.

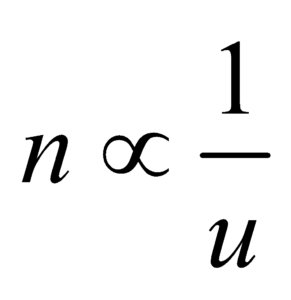
FUNDAMENTAL (OR BASE) AND DERIVED UNITS

Fundamental units are those, which are independent of unit of other physical quantity and cannot be further resolved into any other units or the units of fundamental physical quantities are called fundamental or base units. e.g., kilogram, metre, second etc,
All units other than fundamental are derived units (which are dependent on fundamental units) e.g., unit of speed (ms–1) which depends on unit of length (metre) and unit of time (second), unit of momentum (Kgms–1) depends on unit of mass, length and time etc.

SYSTEM OF UNITS

A system of units is a complete set of fundamental and derived units for all physical quantities.

DIFFERENT TYPES OF SYSTEM OF UNITS

F.P.S. (Foot – Pound – Second) system. (British engineering system of units.): In this system the unit of length is foot, mass is pound and time is second.

 C.G.S. (Centimetre – Gram – Second) system. (Gaussian system of units): In this system the unit of length is centimetre, mass is gram and time is second.

 M.K.S (Metre – Kilogram – Second) system. This system is related to mechanics only. In this system the unit of length is metre, mass is kilogram and time is second.

 S.I.  (International system) units. (Introduced in 1971) Different countries use different set of units. To avoid complexity, by international agreement, seven physical quantities have been chosen as fundamental or base physical quantities and two as supplementary. These quantities are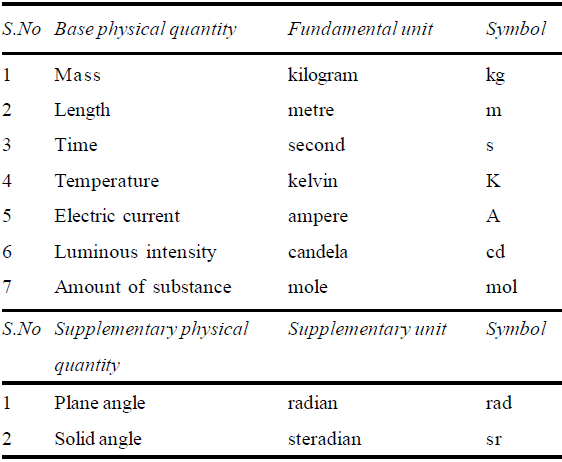

MERITS OF S.I. UNITS

  • SI is a coherent system of units: This means that all derived units are obtained by multiplication and division without introducing any numerical factor.
  • SI is a rational system of units: This is because it assigns only one unit to a particular physical quantity.
  • SI is an absolute system of units: There is no gravitational unit in this system.
  • SI system is applicable to all branches of science.

CONVENTIONS OF WRITING OF UNITS AND THEIR SYMBOLS

  • Unit is never written with capital initial letter.
  • For a unit named after scientist the symbol is a capital letter otherwise not.
  • The unit or symbol is never written in plural form.
  • Punctuations marks are not written after the symbol.

DEFINITIONS OF FUNDAMENTAL UNITS

  • Metre : One metre is equal to 1650763.73 wavelength in vacuum of the radiation corresponding to transition between the levels 2p10 and 5d5 of the krypton – 86 atom
or
The distance travelled by light in vacuum in second is called 1 metre.
  • Kilogram : The mass of cylinder (of height and diameter 39 cm) made of Platinum-iridium alloy kept at International Bureau of weights and measures in paris is defined as 1kg.
  • Second : It is the duration of 9,192,631,770 periods of radiation corresponding to the transition between the two hyperfine levels of the ground state of Caesium (133) atom.
  • Ampere : It is the current which when flows through two infinitely long straight conductors of negligible cross-section placed at a distance of one metre in air or vacuum produces a force of 2 × 10–7 N/m between them.
  • Candela : It is the luminous intensity in a perpendicular direction, of a surface of 1/600,000 square metre of a black body at the temperature of freezing platinum under a pressure of 1.013 × 105 N/m2.
  • Kelvin : It is the 1/273.16 part of thermodynamic temperature of triple point of water.
  • Mole : It is the amount of substance which contains as many elementary entities as there are in 0.012 kg of Carbon-12.

S.I. PREFIXES

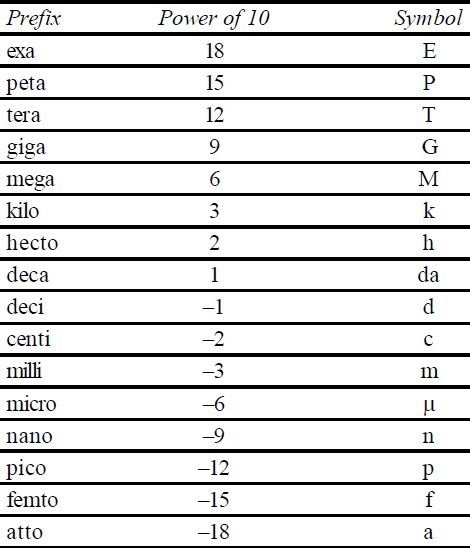
The magnitudes of physical quantities vary over a wide range. For example, the atomic radius, is equal to 10–10m, radius of earth is 6.4×106 m and the mass of electron is 9.1×10–31 kg. The internationally recommended standard prefixes for certain powers of 10 are given in the table:

SOME IMPORTANT PRACTICAL UNITS

  • For large distance (macro-cosm)
Astronomical unit: It is the average distance of the centre of the sun from the centre of the earth.
1 A.U. = 1.496 × 1011m
Light year: It is the distance travelled by the light in vacuum in one year.
1 ly = 9.46 × 1015m
Parsec: One parsec is the distance at which an arc 1A.U. long subtends an angle of one second.
1 parsec = 3.1 × 1016m
  • For small distance (micro-cosm)
1 micron = 10–6m
1 nanometre = 10–9m
1 angstorm = 10–10m
1 fermi = 10–15m
  • For small area
    1 barn = 10–28m2
  • For heavy mass
    1 ton = 1000kg
    1 quintal = 100kg
    1 slug = 14.57kg
    1 C.S.L (chandrasekhar limit) = 1.4 times the mass of the sun
  • For small mass
    1 amu = 1.67 x 10–27kg
    1 pound = 453.6g = 0.4536 kg
  • For small time
    1 shake = 10–8s
  • For large time
Lunar month: It is the time taken by the earth to complete one rotation about its axis with respect to sun.
1L.M.  = 27.3 days.
Solar day: It is the time taken by the earth to complete one rotation about its axis with respect to sun.
Sedrial day: It is the time taken by earth to complete one rotation on its axis with respect to distant star.
  • For measuring pressure
1 bar = 1atm pressure = 105N/m2 = 760mmHg
1torr = 1 mmHg
1 poiseuille = 10 Poise

DIMENSIONS

The powers to which the fundamental units of mass, length and time must be raised to represent the physical quantity are called the dimensions of that physical quantity.
For example :
Force = mass × acceleration
 = mass ×  = [MLT–2]
Hence the dimensions of force are 1 in mass 1 in length and (– 2) in time.

DIMENSIONAL FORMULA

Unit of a physical quantity expressed in terms of M, L and T is called dimensional formula. It shows how and which of the fundamental quantities represent the dimensions.
For example, the dimensional formula of work is [ML2T–2]

DIMENSIONAL EQUATION

When we equate the dimensional formula with the physical quantity, we get the dimensional equation.
For example : Work = [ML2T–2]

CLASSIFICATION OF PHYSICAL QUANTITIES (ON THE BASIS OF DIMENSIONS)

DIMENSIONAL FORMULA OF SOME IMPORTANT PHYSICAL QUANTITIES

 

SHORT CUTS / TIME SAVING TECHNIQUES
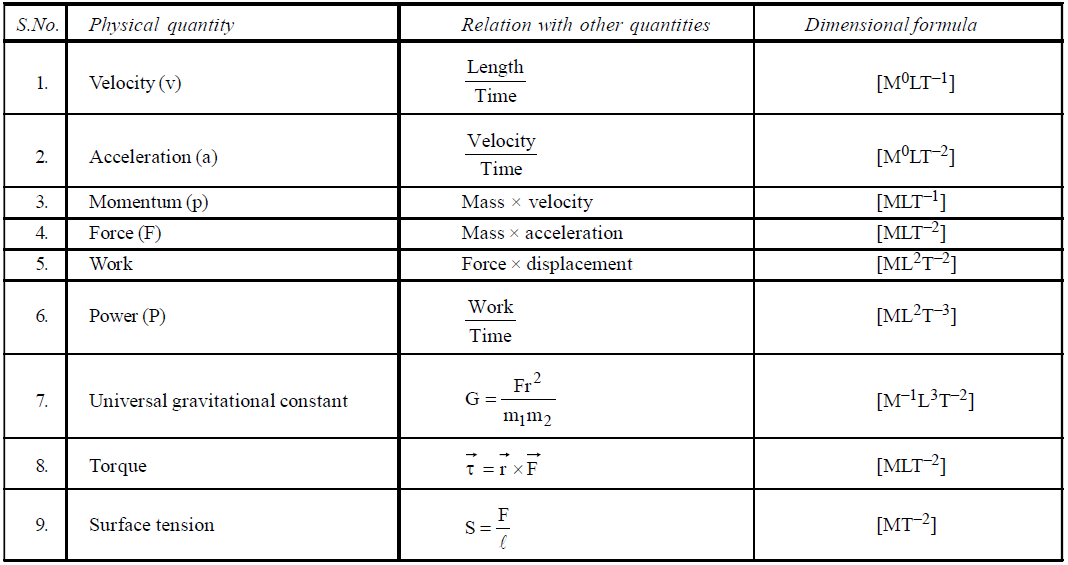
  • To find dimensions of a typical physical quantity which is involved in a number of formulae, try to use that formula which is easiest for you. For example if you want to find the dimensional formula of magnetic induction then you can use the following formulae
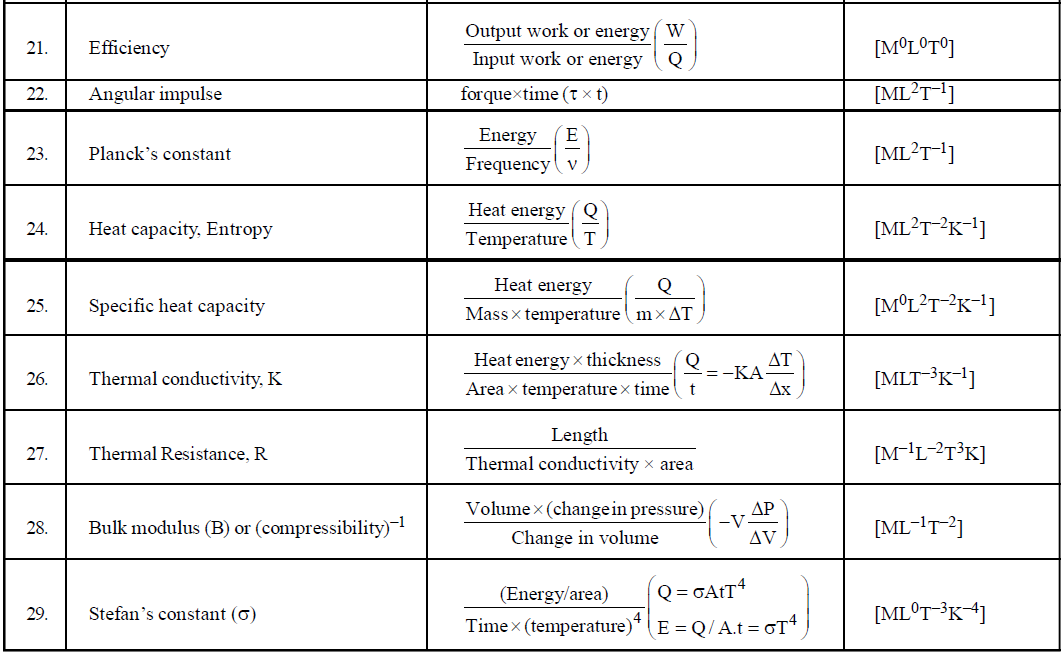
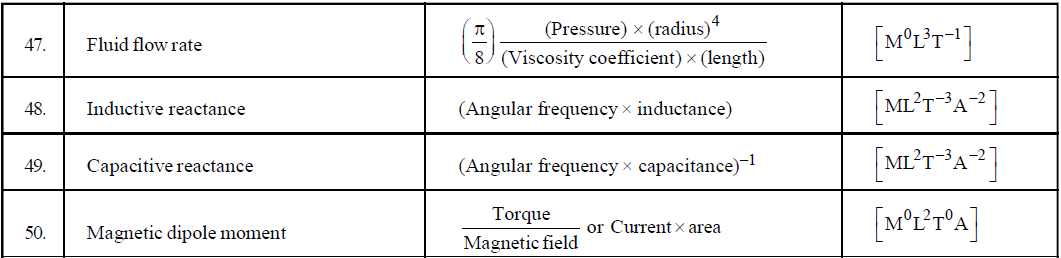
Out of these the easiest is probably the third one.
  • If you have to find the dimensional formula of a combination of physical quantities, then instead of finding the dimensional formula of each, try to correlate the combination of physical quantities with a standard formula. For example, if you have to find the dimension of CV2, then try to use formula 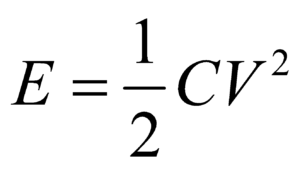where E is energy of a capacitor.
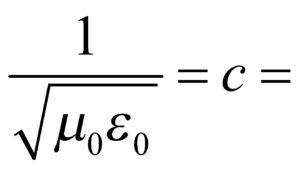  • velocity of light in vacuum
  • Dimensions of the following are same
[ML2T–2]
  • Dimensions of the following are same
Force = Impulse / time
= q v B = q E
= Thrust
= weight  = energy gradient   [MLT–2]
  • The dimension of RC = 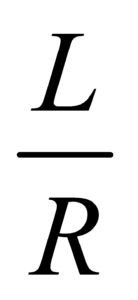is same as that of time
  • Dimensions of the following are same
Velocity =     [M°LT–1]
  • Dimensions of the following are same
Frequency   [M°L°T–1]
  • Dimensions of the following are same
(E) Modulus of elasticity = Y (Young’s modulus)
               = B (Bulk modulus)
   = η (Modulus of rigidity)
    = Stress
  = Pressure = [ML–1T–2]
  • Dimensions of the following are same
Acceleration, retardation, centripetal acceleration, centrifugal acceleration, gravitational intensity/strength.       [M°LT–2]
  • Dimensions of the following are same
Water equivalent, thermal capacity, entropy, Boltzmann’s constant. [ML2T–2K–1]

 KEEP IN MEMORY

The dimensional formula of
  • all trigonometric ratio is [M0L0T0]
  • x in ex is [M0L0T0]
  • ex is [M0L0T0]
  • x in log x is [M0L0T0]
  • log x is [M0L0T0]

DIMENSIONAL ANALYSIS AND ITS APPLICATIONS

Principle of Homogeneity : Only those physical quantities can be added /subtracted/equated /compared which have the same dimensions.

 USES OF DIMENSIONS

  1. Conversion of one system of unit into another
Example : Convert a pressure of 106 dyne/cm2 in S.I units.
Sol. We know that 1N = 105 dyne ⇒ 1 dyne = 10–5 N
Also 1m = 100 cm ⇒ 1cm = 10–2 m
Now, the pressure 106 dyne/cm2 in SI unit is
  1. Checking the accuracy of various formulae
Example : Check the correctness of the following equation dimensionally
f = η A ( dv/dx) (sin θ) where F = force, η  = coefficient of viscosity, A = area, gradient w.r.t distance, θ = angle of contact
Sol. L.H.S = force = [MLT–2]
R.H.S =
The equation is dimensionally correct.
  1. Derivation of formula
Example : The air bubble formed by explosion inside water performed oscillation with time period T which is directly proportional to Pa db Ec where P is pressure, d is density and E is the energy due to explosion. Find the values of a, b and c.
Sol. Let us assume that the required expression for time period is T = K Pa db Ec
where K is a dimensionless constant.
Writing dimensions on both sides,
Equating the powers,
a +  b + c = 0 ….(1)
– a  – 3b + 2c = 0 ….(2)
– 2a – 2c = 1 ….(3)
Solving these equations,  we get,
a = -5/6, b =1/2 , c = 1/3.

LIMITATIONS OF DIMENSIONAL ANALYSIS

  • No information about the dimensionless constant is obtained during dimensional analysis
  • Formula cannot be found if a physical quantity is dependent on more than three physical quantities.
  • Formula containing trigonometrical /exponential function cannot be found.
  • If an equation is dimensionally correct it may or may not be absolutely correct.

SIGNIFICANT FIGURES

The number of digits, which are known reliably in our measurement, and one digit that is uncertain are termed as significant figures.

RULES TO DETERMINE THE NUMBERS OF SIGNIFICANT FIGURES

  1. All non-zero digits are significant. 235.75 has five significant figures.
  2. All zeroes between two non-zero digits are significant. 2016.008 has seven significant figures.
  3. All zeroes occurring between the decimal point and the non-zero digits are not significant provided there is only a zero to left of the decimal point.  0.00652 has three significant figures.
  4. All zeroes written to the right of a non-zero digit in a number written without a decimal point are not significant. This rule does not work if zero is a result of measurement. 54000 has two significant figures whereas 54000m has five significant figures.
  5. All zeroes occurring to the right of a non-zero digit in a number written with a decimal point are significant. 32.2000 has six significant figures.
  6. When a number is written in the exponential form, the exponential term does not contribute towards the significant figures. 2.465 × 105 has four significant figures.

 KEEP IN MEMORY

  • The significant figures depend upon the least count of the instrument.
  • The number of significant figure does not depend on the units chosen.

ROUNDING OFF

  • If digit to be dropped is less than 5 then preceding digit should be left unchanged.
  • If digit to be dropped is more than 5 then one should raise preceding digit by one.
  • If the digit to be dropped is 5 followed by a digit other than zero then the preceding digit is increased by one.
  • If the digit to be dropped is 5 then the preceding digit is not changed if it is even.
  • If digit to be dropped is 5 then the preceding digit is increased by one if it is odd.

ARITHMETICAL OPERATIONS WITH SIGNIFICANT FIGURES AND ROUNDING OFF

  • For addition or subtraction, write the numbers one below the other with all the decimal points in one line. Now locate the first column from the left that has a doubtful digit. All digits right to this column are dropped from all the numbers and rounding is done to this column.  Addition subtraction is then done.
Example : Find the sum of 23.623 and 8.7 to correct significant figures.
Sol. Step-1 :- 23.623 + 8.7
Step-2 :-  23.6 + 8.7=32.3
  • In multiplication and division of two or more quantities, the number of significant digits in the answer is equal to the number of significant digits in the quantity, which has minimum number of significant digits.
The insignificant digits are dropped from the result if they appear after the decimal point. They are replaced by zeroes if they appear to the left of the decimal point. The least significant digit is rounded off.
Example : 107.88 (5. S. F.) × 0.610 (3 S. F.) =  65.8068 ≅ 65.8

ACCURACY, PRECISION OF INSTRUMENTS AND ERRORS IN MEASUREMENTS

Accuracy and Precision are two terms that have very different meanings in experimental physics. We need to be able to distinguish between an accurate measurement and a precise measurement. An accurate measurement is one in which the results of the experiment are in agreement with the ‘accepted’ value.
Note:- This only applies to experiments where this is the goal like measuring the speed of light. A precise measurement is one that we can make to a large number of decimal places.

 The following diagrams illustrate the meaning of terms accuracy and precision

In the above figure : The centre of the target represents the accepted value. The closer to the centre, the more accurate the experiment. The extent of the scatter of the data is a measure of the precision.
A – Precise and accurate
B – Accurate but imprecise
C – Precise but not accurate
D – Not accurate nor precise
When successive measurements of the same quantity are repeated there are different values obtained. In experimental physics it is vital to be able to measure and quantify this uncertainty. (The words “error” and “uncertainty” are often used interchangeably by physicists – this is not ideal – but get used to it!)

 

Error in measurements is the difference of actual or true value and measured value.
Error = True value – Measured value

 

KEEP IN MEMORY
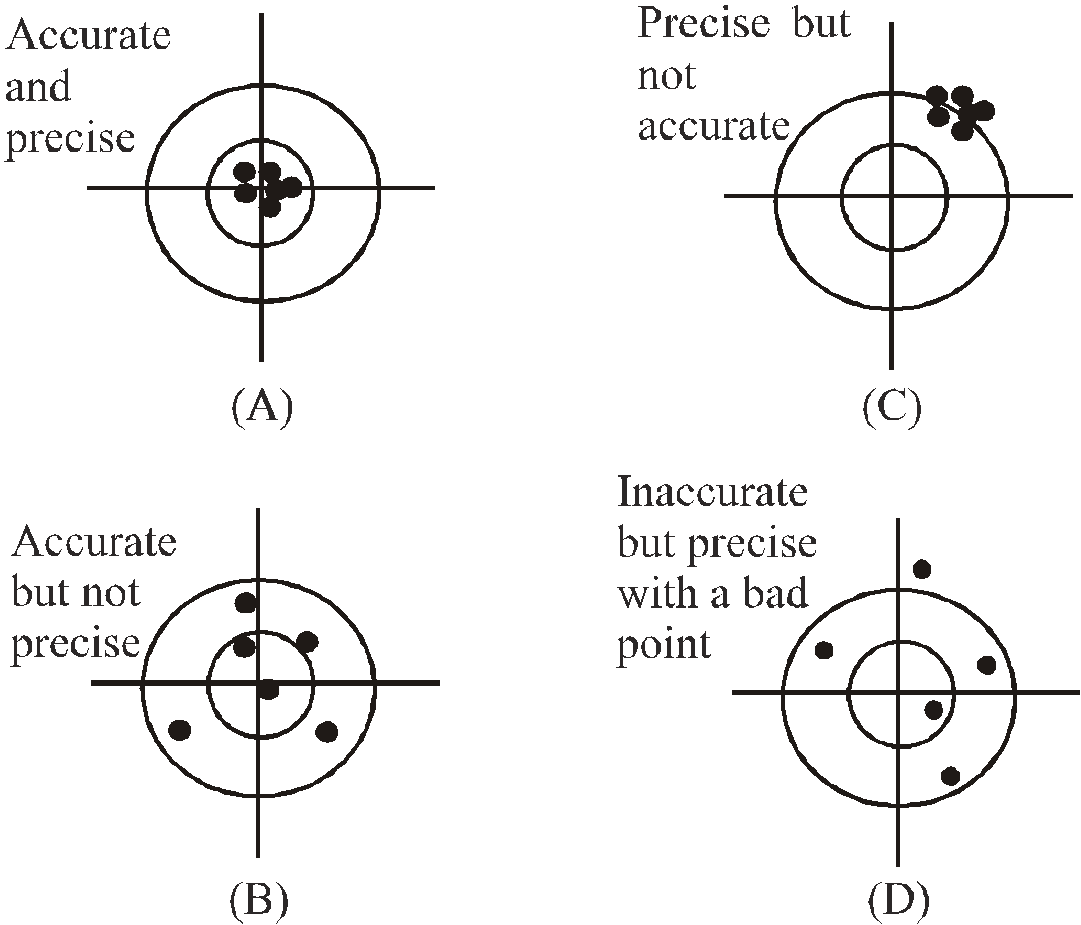
  1. Accuracy depends on the least count of the instrument used for measurement.
  2. In the addition and subtraction operation, the result contains the minimum number of decimal places of the figures being used
  3. In the multiplication and division operation, the result contains the minimum number of significant figures.
  4. Least count (L.C.) of vernier callipers =  one MSD – one VSD
where MSD = mains scale division, VSD = vernier scale division
  1. Least count of screw gauge  (or spherometer)
    where pitch is the ratio of number of  divisions moved on linear scale and number of rotations given to circular scale.
  2. Pure number or unmeasured value do not have significant numbers
  3. Change in the position of decimal does not change the number of significant figures. Similarly the change in the units of measured value does not change the significant figures.

COMMON ERRORS IN MEASUREMENTS

It is not possible to measure the 100% correct value of any physical quantity, even after measuring it so many times. There always exists some uncertainty, which is usually referred to as experimental error.

EXPERIMENTAL ERRORS

Random error : It is the error that has an equal chance of being positive or negative.
It occurs irregularly and at random in magnitude and direction. It can be caused
  • by the lack of perfection of observer
  • if the measuring instrument is not perfectly sensitive.

 

Systematic error :  It tends to occur in one direction either positive or negative. It occurs due to
  • measuring instrument having a zero error.
  • an instrument being incorrectly calibrated (such as slow- running-stop clock)
  • the observer persistently carrying out a mistimed action (e.g., in starting and stopping a clock)
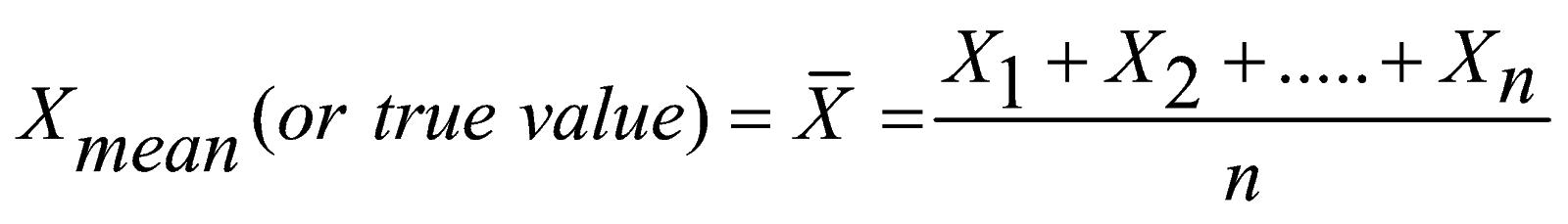
For measuring a particular physical quantity, we take a number of readings. Let the readings be X1, X2…………,Xn. Then the mean value is found as follows

METHODS OF EXPRESSING ERROR

Absolute error :  It is the difference between the mean value and the measured value of the physical quantity.
|ΔX1|  = |Xmean–X1|  
…………………………….
…………………………….
|ΔXn|  = |Xmean–Xn|  
Mean absolute error:
ΔXmean or =

 

Relative error : It is the ratio of the mean absolute error and the value of the quantity being measured.

 

Percentage error : It is the relative error expressed in percent
Percentage error

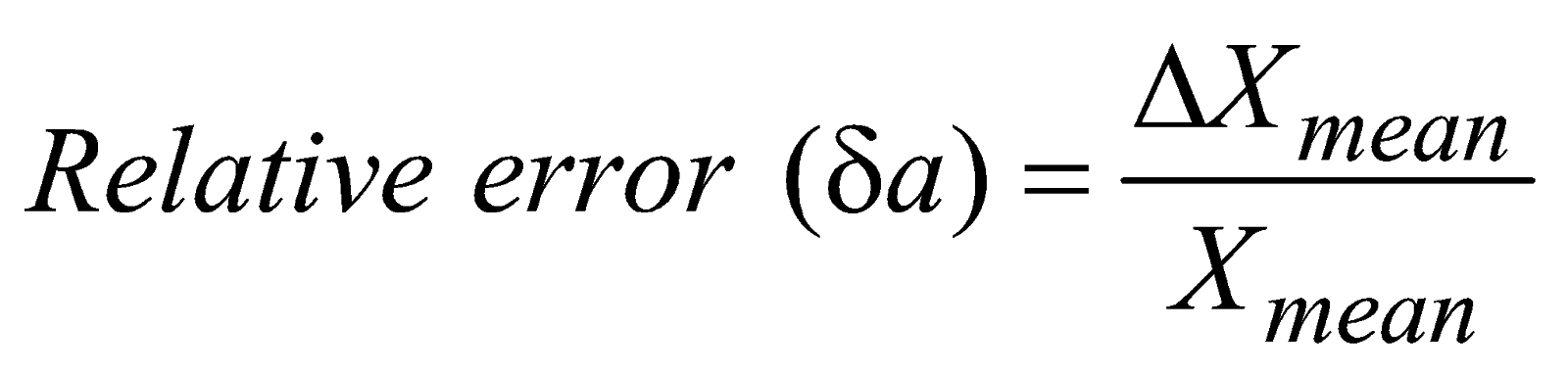
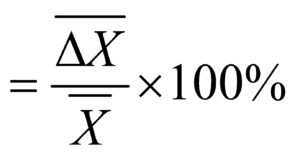
TO FIND THE MAXIMUM ERROR IN COMPOUND QUANTITIES

SUM AND DIFFERENCE
We have to find the sum or difference of two values given as (a ± Δa) and (b ± Δb), we do it as follows
X ± ΔX = (a ± Δa) + (b ± Δb) = (a + b) ± (Δa + Δb)
⇒ X = a + b and ΔX = Δa + Δb in case of sum
And X = (a – b) and ΔX = Δa + Δb in case of difference.

 PRODUCT AND QUOTIENT
We add the fractional or percentage errors in case of finding product or quotient.

If P = ab then
If  then

 

POWER OF A QUANTITY
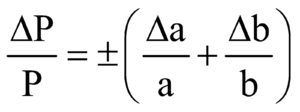
If  x = an then
Example :   
For, If and
Then × 100 = (2 × 3 + 4)% = 10%
Similarly :

 

KEEP IN MEMORY
  1. More the accuracy, smaller is the error.
  2. Absolute error |ΔX| is always positive.
  3. |ΔX| has the same dimensions as that of X.
  4. If the least count of measuring instrument is not given and the measured value is given the least error in the measurement can be found by taking the last digit to be 1 and rest digit to be zero. For e.g. if the measured value of mass m = 2.03 kg then.
  5. If a number of physical quantities are involved in an expression then the one with higher power contributes more in errors and therefore should be measured more accurately.
  6. Relative error is a dimensionless quantity.
  7. We are always interested in calculating the maximum possible error.

The realm of physics

1.1.1 State and compare quantities to the nearest order of magnitude.

Throughout the study of physics we deal with a wide range of magnitudes. We will use minuscule values such as the mass of an electron and huge ones such as the mass of the (observable) universe. In order to easily understand the magnitude of these quantities we need a way to express them in a simple form, to do this, we simply write them to the nearest power of ten (rounding up or down as appropriate).

That is, instead of writing a number such as 1000, we write 103 .

The use of orders of magnitude is generally just to get an idea of the scale and differences in scale of values. It is not an accurate representation of a value. For example, if we take 400, it’s order of magnitude is 102 , which when we calculate it gives 10 x 10 = 100. This is four times less than the actual value, but that does not matter. The point of orders of magnitude is to get a sense of the scale of the number, in this case we know the number is within the 100s.

1.1.2 State the ranges of magnitude of distances, masses and times that occur in the universe, from smallest to greatest.

Distances:

  • sub-nuclear particles: 10-15 m
  • extent of the visible universe: 10+25 m

Masses:

  • mass of electron: 10-30 kg
  • mass of universe: 10+50 kg

Times:

  • passage of light across a nucleus: 10-23 s
  • age of the universe : 10+18 s

1.1.3 State ratios of quantities as differences of orders of magnitude.

Using orders of magnitude makes it easy to compare quantities, for example, if we want to compare the size of an an atom (10-10 m) to the size of a single proton (10-15 m) we would take the difference between them to obtain the ratio. Here, the difference is of magnitude 105meaning that an atom is 105 or 100000 times bigger than a proton.

1.1.4 Estimate approximate values of everyday quantities to one or two significant figures and/or to the nearest order of magnitude.

Significant figures
To express a value to a certain amount of significant figures means to arrange the value in a way that it contains only a certain amount of digits which contribute to its precision.

For example, if we were asked to state the value of an equation to three significant figures and we found the result of that value to be 2.5423, we would state it as 2.54.

Note that 2.54 is accurate to three significant figures as we count both the digits before and after the point.

The amount of significant figures includes all digits except:

  • leading and trailing zeros (such as 0.0024 (2 sig. figures) and 24000 (2 sig. figures)) which serve only as placeholders to indicate the scale of the number.
  • extra “artificial” digits produced when calculating to a greater accuracy than that of the original data, or measurements reported to a greater precision than the equipment used to obtain them supports.

Rules for identifying significant figures:

  • All non-zero digits are considered significant (such as 14 (2 sig. figures) and 12.34 (4 sig. figures)).
  • Zeros placed in between two non-zero digits (such as 104 (3 sig. figures) and 1004 (4 sig. figures))
  • Trailing zeros in a number containing a decimal point are significant (such as 2.3400 (5 sig. figures) note that a number 0.00023400 also has 5 sig. figures as the leading zeros are not significant).

Note that a number such as 0.230 and 0.23 are technically the same number, but, the former (0.230) contains three significant figures, which states that it is accurate to three significant figures. On the other hand, the latter (0.23) could represent a number such as 2.31 accurate to only two significant figures. The use of trailing zeros after a decimal point as significant figures is is simply to state that the number is accurate to that degree.

Another thing to note is that some numbers with no decimal point but ending in trailing zeros can cause some confusion. For example, the number 200, this number contains one significant figure (the digit 2). However, this could be a number that is represented to three significant figures which just happens to end with trailing zeros.

Typically these confusions can be resolved by taking the number in context and if that does not help, one can simply state the degree of significance (for example “200 (2 s.f.)” , means that the two first digits are accurate and the second trailing zero is just a place holder.

Expressing significant figures as orders of magnitude:
To represent a number using only the significant digits can easily be done by expressing it’s order of magnitude. This removes all leading and trailing zeros which are not significant.

For example:
0.00034 contains two significant figures (34) and fours leading zeros in order to show the magnitude. This can be represented so that it is easier to read as such: 3.4 x 10-4 .

Note that we simply removed the leading zeros and multiplied the number we got by 10 to the power of negative the amount of leading zeros (in this case 4). The negative sign in the power shows that the zeros are leading.

A number such as 34000 (2 s.f.) would be represented as 34 x 103 .

Again, we simply take out the trailing zeros, and multiply the number by 10 to the power of the number of zeros (3 in this case).

There are a couple of cases in which you need to be careful:

  • A number such as 0.003400 would be represented as 3.400 x 10-3 . Remember, trailing zeros after a decimal point are significant.
  • 56000 (3 s.f.) would be represented as 560 x 102 . This is because it is stated that the number is accurate the 3 significant zeros, therefor the first trailing zero is significant and must be included. Note that this can be used as another way to express a value such as 56000 to three significant figures (as opposed to writing “56000 (3 s.f.)”).

Rounding
When working with significant figures you will often have to round numbers in order to express them to the appropriate amount of significant figures.

For example:
State 2.342 to three significant figures: would be written 2.34.

When representing the number 2.342 to three significant figures we rounded it down to 2.34. This means that when we removed the excess digit, it was not high enough to affect the last digit that we kept.

Whether to round up or down is a simple decision:
If the first digit in the excess being cut off is lower than 5 we do not change the last digit which we are keeping. If the first digit in the excess which is being cut off is 5 or higher we increment the last digit that we are keeping (and the rest of the number if required).

For example:
State 5.396 to three significant figures: would be written 5.40. This is because we remove the last digit (6) in order to have three significant digits. However, 6 is large enough for it to affect the digit before it, therefor we increment the last digit of the number we are keeping by 1. Note that the last digit of the number that we are keeping is 9, therefor incrementing it by 1 gives 10. Thus we also need to increment the second to last digit by 1. This gives 5.40 which is accurate to three significant figures.

You might think that if a number such as 5.4349 were to be rounded to 3 s.f. it would give 5.44 as the last digit is 9 which is large enough to affect the previous digit which would then become 5. Now that 5 would be large enough to affect the last digit of the number we are keeping which would become 4 (thus 5.44). However, this is not the case, when rounding, we only look at the digit immediately after the one we are rounding to, whether or not that digit would be affected by the one after it is not taken into account. Therefor, the correct result of this question would be 5.43.

1.1.1 State and compare quantities to the nearest order of magnitude.
An order of magnitude indicates the relative size of a quantity. Long and complicated numbers can be simplified or estimated through the use of this method. For example, the number 200 is in the order of magnitude of 10^2 (100). When estimating orders of magnitude — similar to rounding — anything below 5 is the lower order of magnitude while anything above or equal to 5 is the higher order of magnitude. In this case, 500 and anything above would be in the order of magnitude of 10^3 (1000). Some common orders of magnitude include:

 
Practice questions
1. Estimate the number of seconds in a human “lifetime”.
Answer: 70yrs = 2.2 * 10^9 sec, 100yrs = 3.1 * 10^9 sec, 50yrs = 1.6 * 10^9 sec, therefore the estimate of the order of magnitude is 10^9 sec.
1.1.2 State the ranges of magnitude of distances, masses and times that occur in the universe, from smallest to greatest.

 

 

 
 
 
1.1.3 State ratios of quantities as differences of orders of magnitude.
Orders of magnitude can be compared in order to create a ratio. For example, the size of an atom is 10^-10m whereas the size of a proton is 10^-15m. The difference between these two values is 10^-5, so the atom is 10^5 (100,000) times bigger than a proton. The ratio of the atom to the proton would be 1:10^-5.
Practice questions
1. Estimate the ratio of
a) the mass of an electron to the mass of a human
b) the radius of earth to the size of the universe
Answers:
1. a) compare 10^-30 and 10^2, 10^32 is the difference hence 1:10^32  b) compare 10^7 and 10^26, 10^19 is the difference hence 1:10^19
1.1.4 Estimate approximate values of everyday quantities to one or two significant figures and/or to the nearest order of magnitude.

Significant figures are the individual digits in a numerical value. For example, the number 20 has two significant figures. One important rule regarding significant figures is that when there are zeroes preceding the number (ie. 0.020), they are not counted, hence the value 0.020 would still have two significant figures. Zeroes after the number (ie. 20.00) or between values (ie. 201) are always counted.

In order to express significant figures as orders of magnitude, one should take all of the numbers following the amount of significant figures given and convert them to a power of 10. For example, the number 0.0030 would be 3.0 × 10^-4; the zero after 3 remains because it was significant in the original value. Sometimes a significant figure amount will be given to you, for example, “56,000 (3 s.f.)” would convert to 560*10^2 because 560 has three significant figures and that was the requested amount in the original question.

Sometimes numbers need to be rounded in order to fit a significant figure amount. If the amount of significant figures required is two and your answer is “56,000”, you should rewrite it as “5.6 × 10^4”. Similarly, if your answer is “0.0560823” and you require two significant figures, you should round it down to “0.056” or rewrite it as “5.6 × 10^-2”.

Scroll to Top