2.2 Forces
Essential Idea:
Classical physics requires a force to change a state of motion, as suggested by Newton in his laws of motion.
Understandings:
- Objects as point particles
- Free-body diagrams
- Translational equilibrium
- Newton’s laws of motion
- Solid friction
Applications and Skills:
- Representing forces as vectors
- Sketching and interpreting free-body diagrams
- Describing the consequences of Newton’s first law for translational equilibrium
- Using Newton’s second law quantitatively and qualitatively
- Identifying force pairs in the context of Newton’s third law
- Solving problems involving forces and determining resultant force
- Describing solid friction (static and dynamic) by coefficients of friction
LAWS OF MOTION
ARISTOTLE’S FALLACY
According to Aristotelian law an external force is required to keep a body in motion. However an external force is required to overcome the frictional forces in case of solids and viscous forces in fluids which are always present in nature.
LINEAR MOMENTUM (P)
Linear momentum of a body is the quantity of motion contained in the body. Momentum 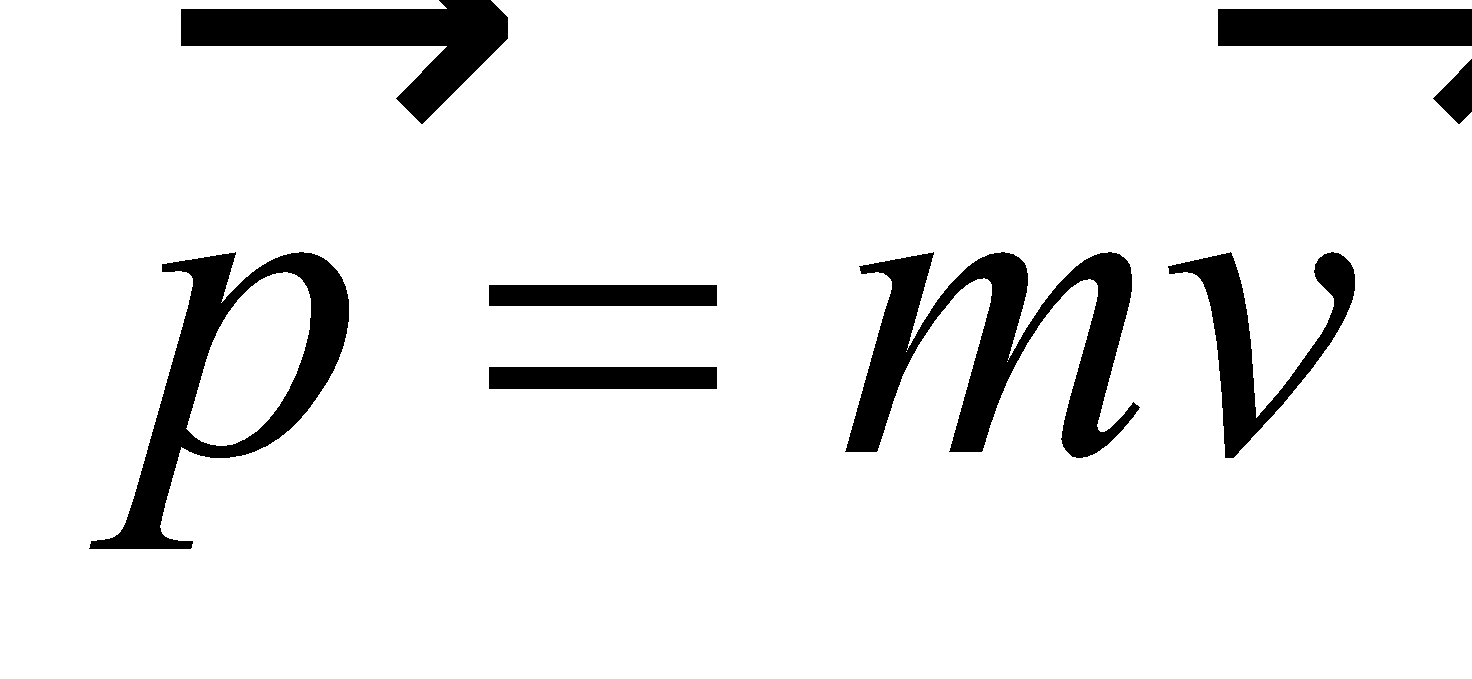
It is a vector quantity having the same direction as the direction of the velocity. Its SI unit is kg ms–1.
NEWTON’S LAWS OF MOTION
FIRST LAW
A body continues to be in a state of rest or of uniform motion, unless it is acted upon by some external force to change its state.
Newton’s first law gives the qualitative definition of force according to which force is that external cause which tends to change or actually changes the state of rest or motion of a body.
Newton’s first law of motion is the same as law of inertia given by Galileo.
Inertia is the inherent property of all bodies because of which they cannot change their state of rest or of uniform motion unless acted upon by an external force.
SECOND LAW
The rate of change of momentum of a body is directly proportional to the external force applied on it and the change takes place in the direction of force applied.
i.e., 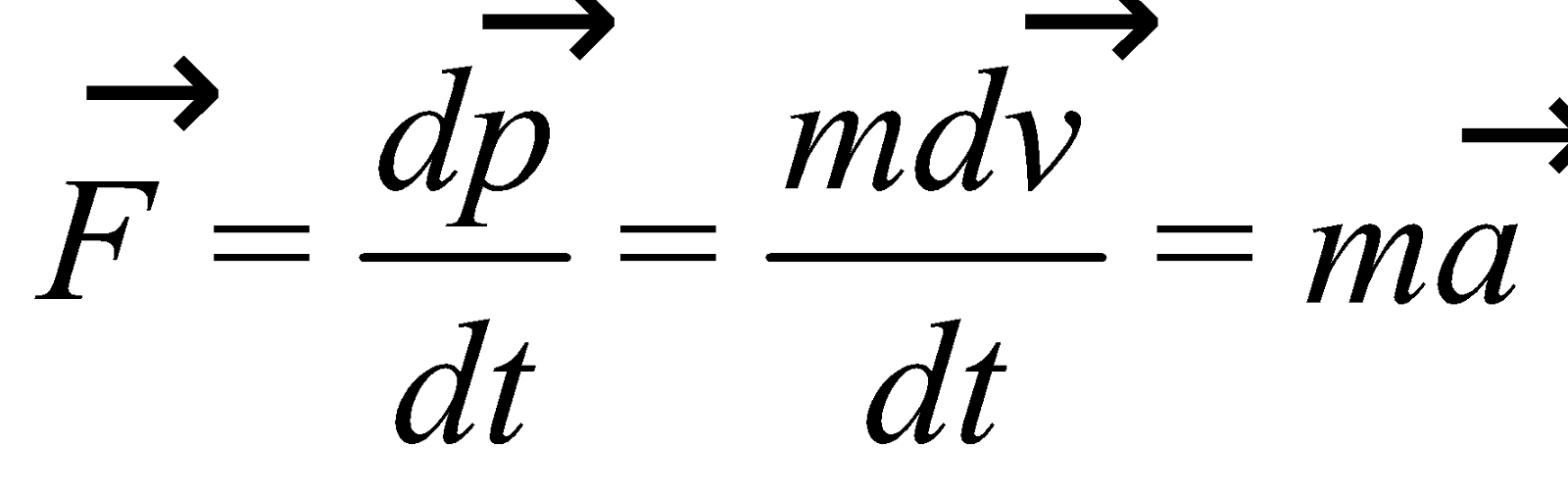
This is the equation of motion of constant mass system. For variable mass system such as rocket propulsion
The SI unit of force is newton. (One newton force is that much force which produces an acceleration of 1ms–2 in a body of mass 1 kg.
The CGS unit of force is dyne. (1N = 105 dyne)
The gravitational unit of force is kg-wt (kg-f) or g-wt (g-f)
1 kg-wt (kg-f) = 9.8 N, 1 g-wt (g-f) = 980 dyne
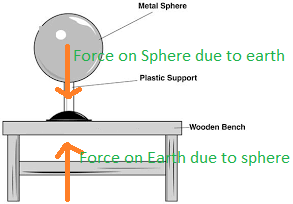
THIRD LAW
To every action there is an equal and opposite reaction. For example – walking , swimming , a horse pulling a cart etc.
Action and reaction act on different bodies and hence cannot balance each other. Action and reaction occur simultaneously. Forces always occur in pairs.
EQUILIBRIUM OF A PARTICLE
A body is said to be in equilibrium when no net force acts on the body.
i.e., 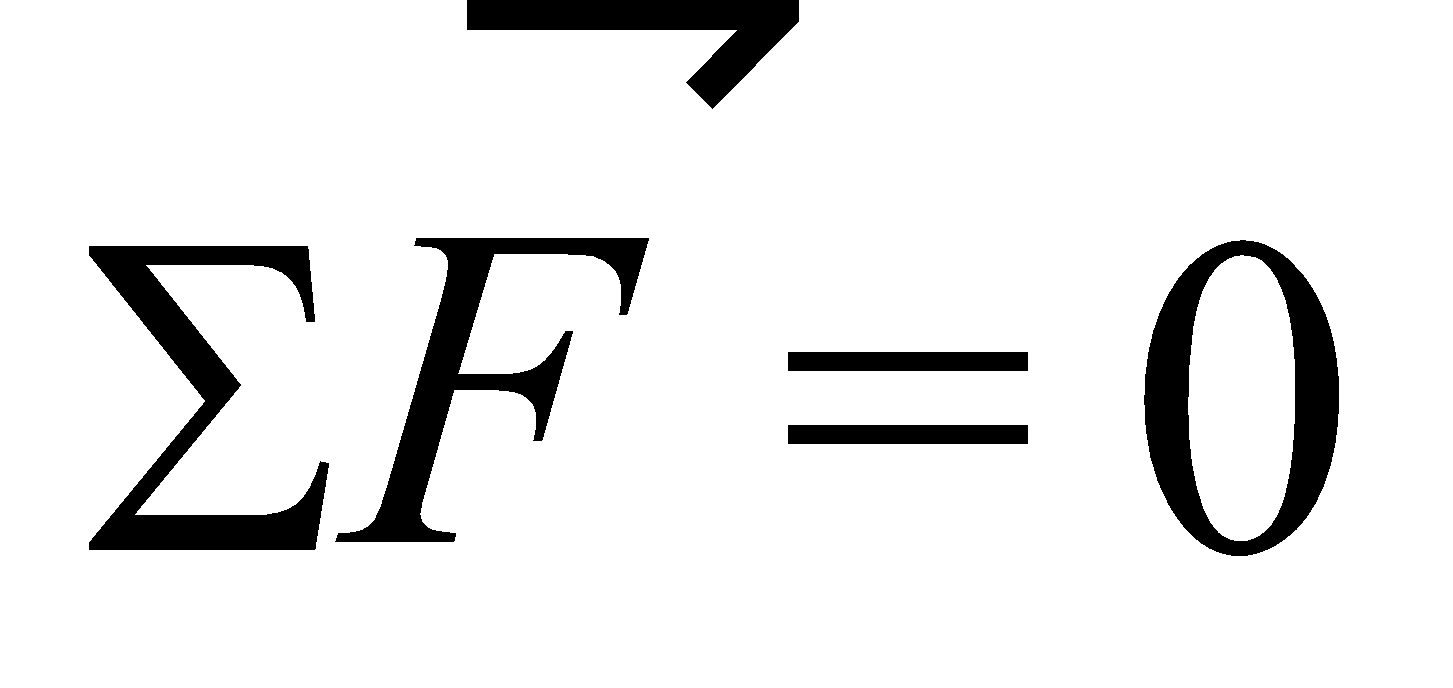
Then  and
and 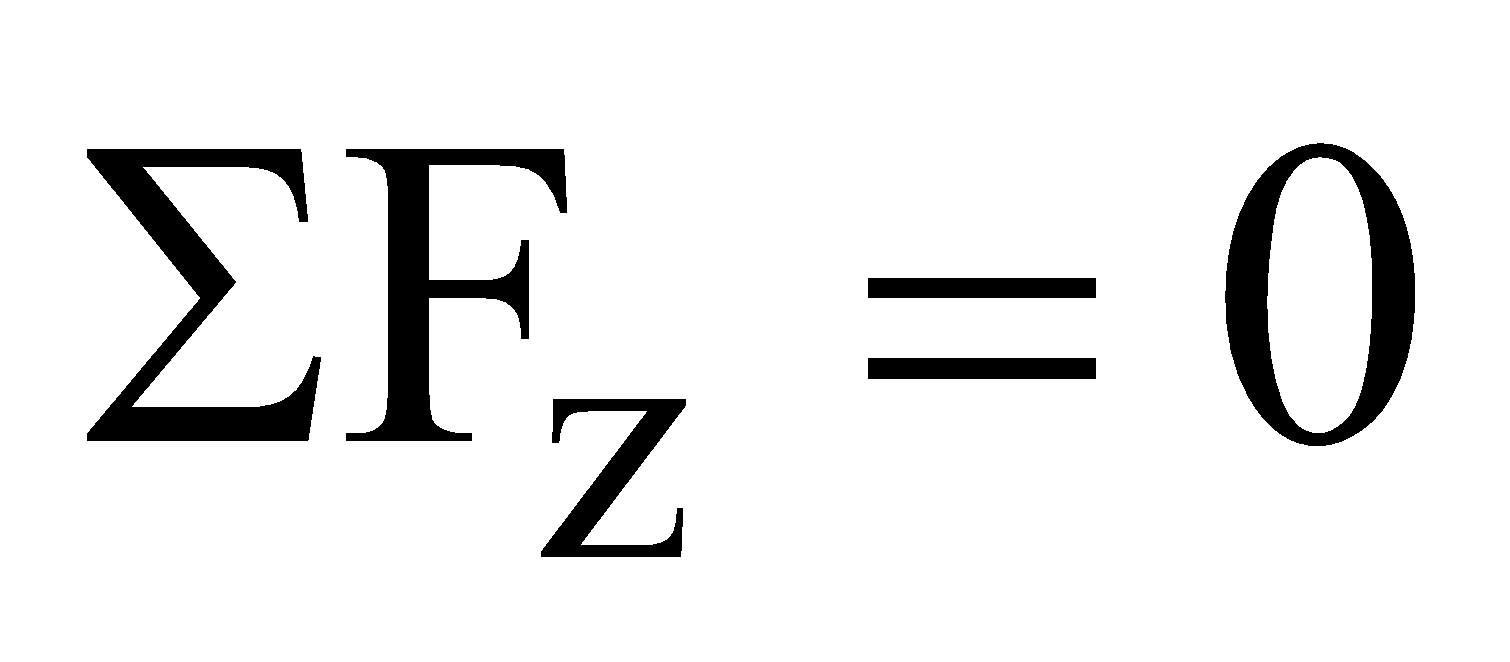
STABLE EQUILIBRIUM
If a body is slightly displaced from equilibrium position, it has the tendency to regain its original position, it is said to be in stable equilibrium.
In this case, P.E. is minimum. 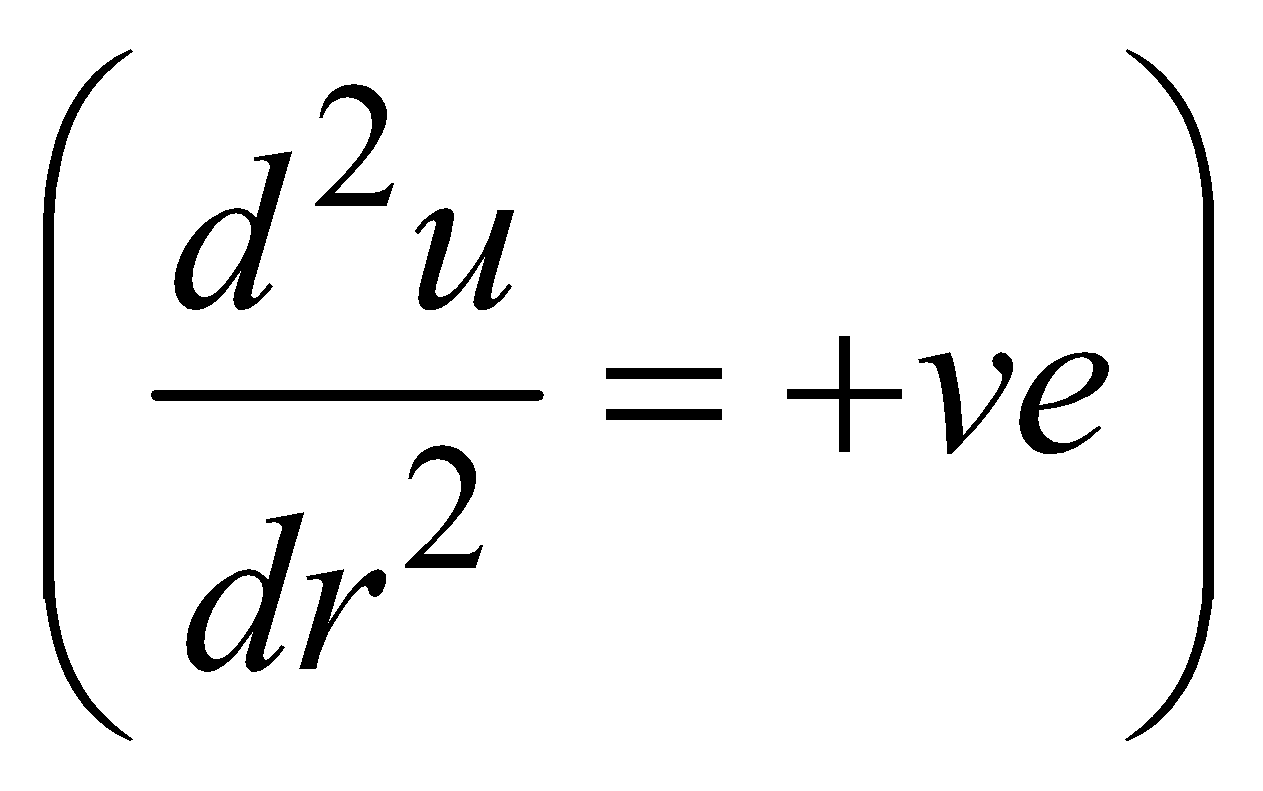
So, the centre of gravity is lowest.
UNSTABLE EQUILIBRIUM
If a body, after being displaced from the equilibrium position, moves in the direction of displacement, it is said to be in unstable equilibrium.
In this case, P.E. is maximum. 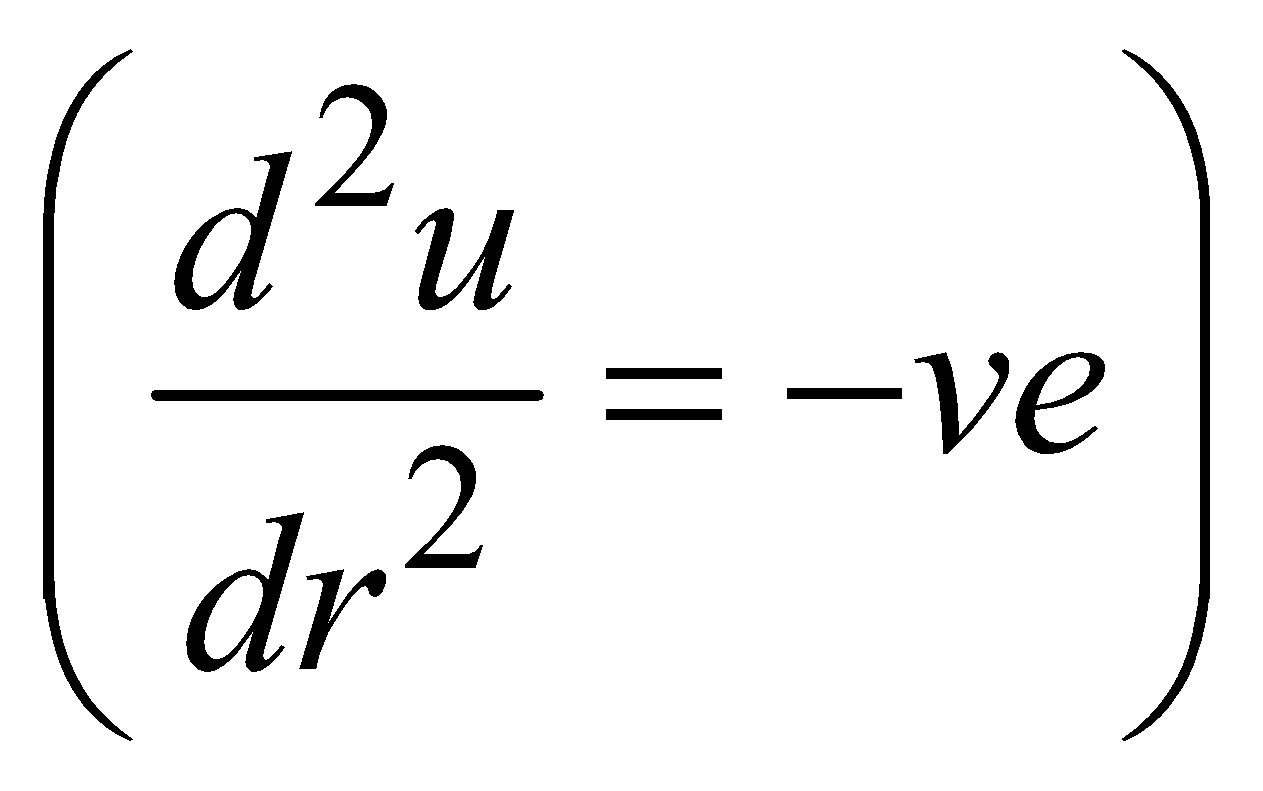
So, the centre of gravity is highest.
NEUTRAL EQUILIBRIUM
If a body, after being slightly displaced from the equilibrium position has no tendency to come back or to move in the direction of displacement the equilibrium is known to be neutral.
In this case, P.E. is constant 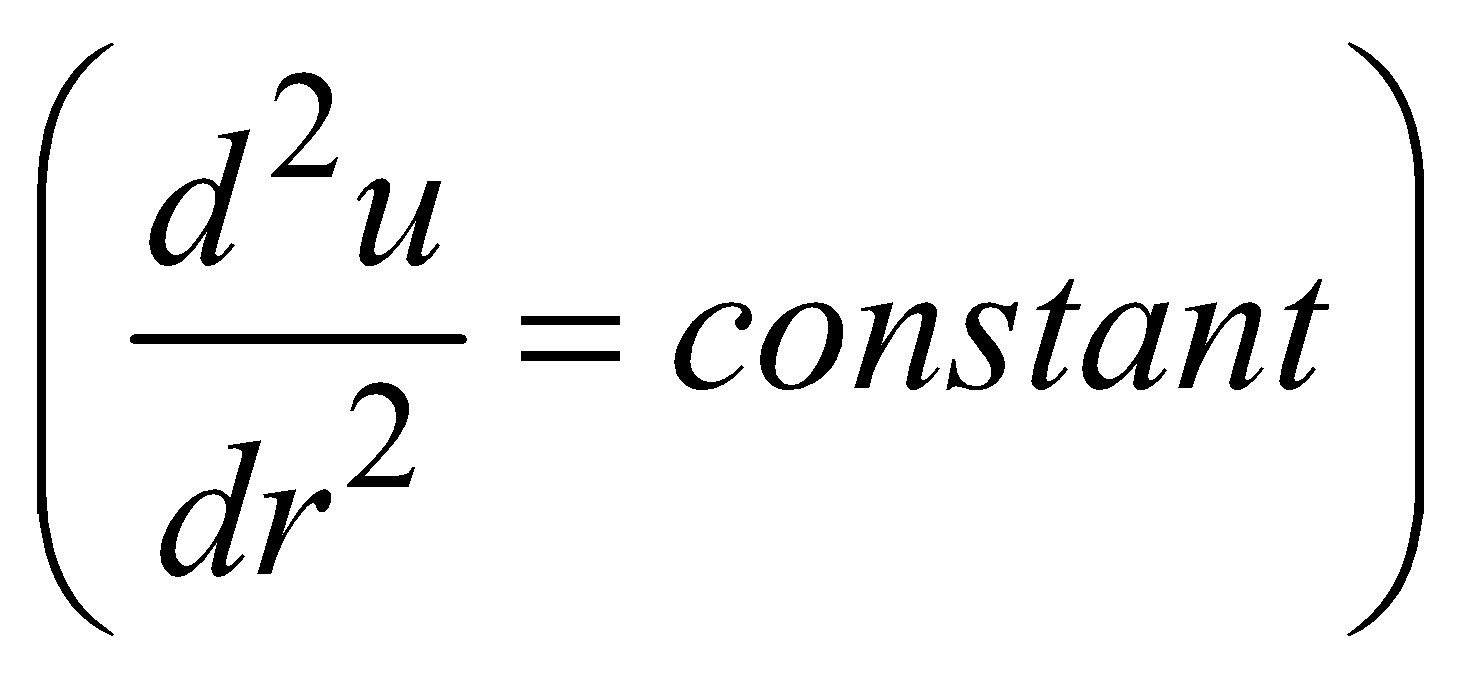
The centre of gravity remains at constant height.
COMMON FORCES IN MECHANICS
WEIGHT
It is the force with which the earth attracts a body and is called force of gravity, For a body of mass m, where acceleration due to gravity is g, the weight W = mg
TENSION
The force exerted by the ends of a loaded/stretched string (or chain) is called tension. The tension has a sense of pull at its ends.
Case 1 

Case 2 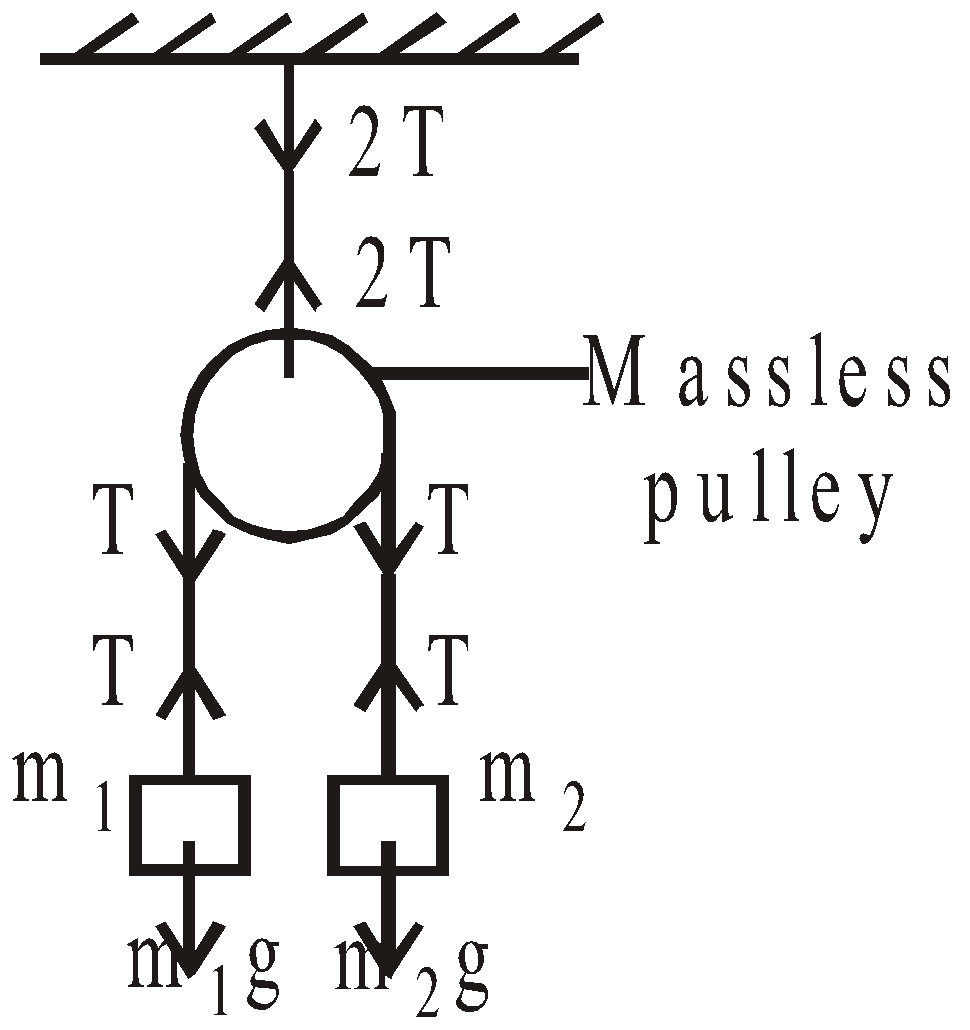

Case 3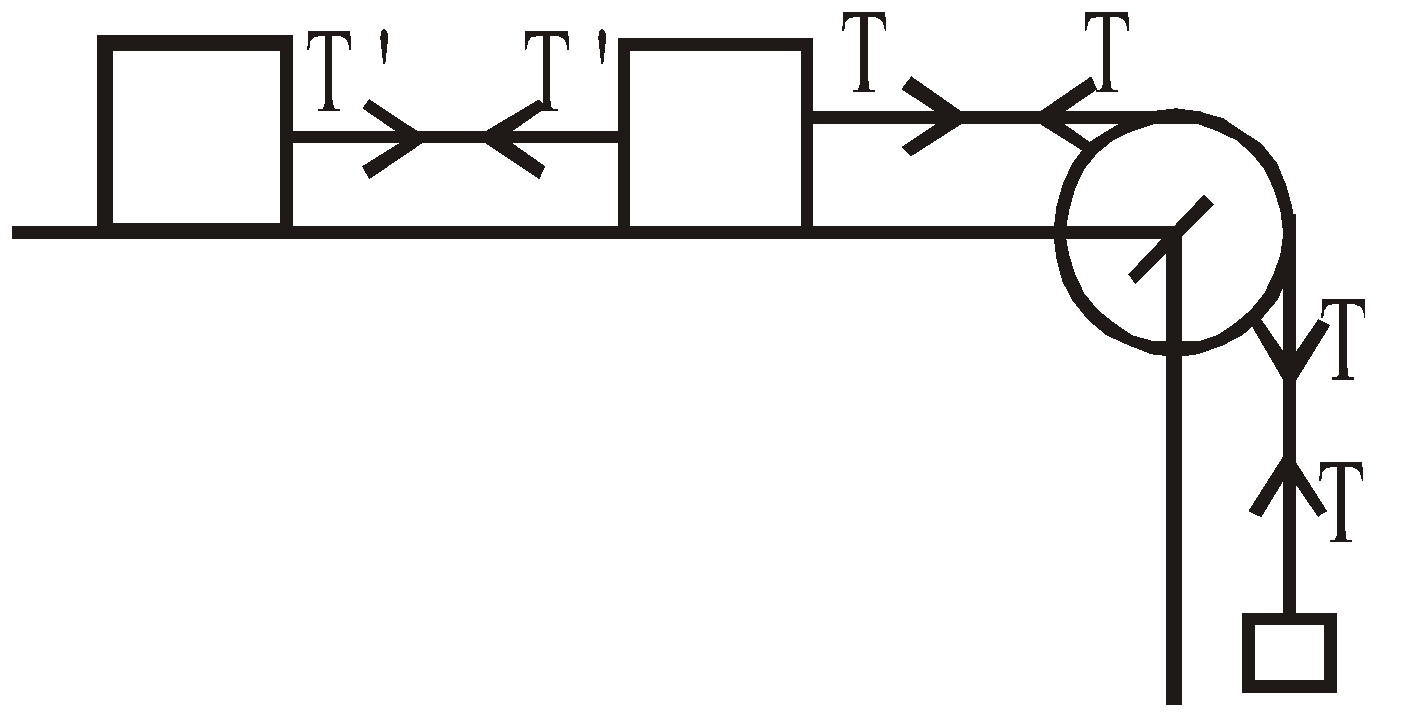
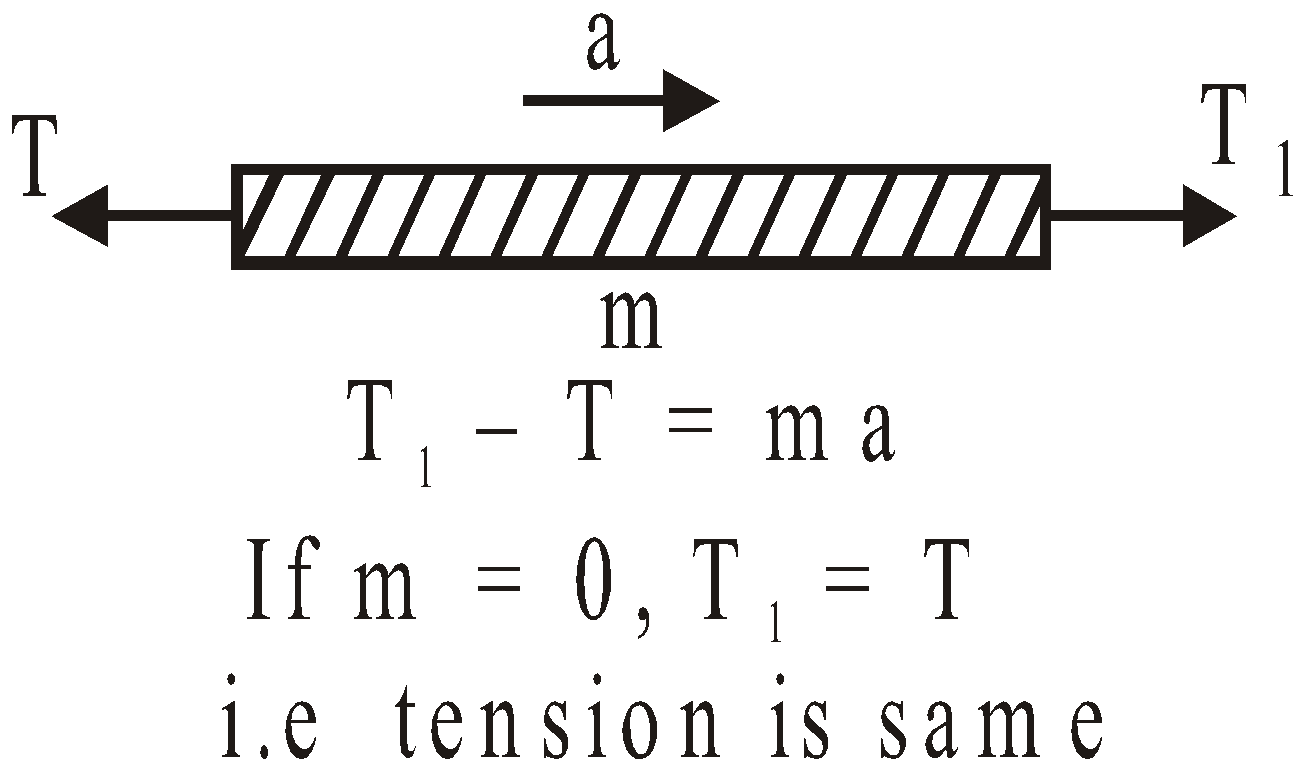


The tension in a string remains the same throughout the string if
(a) string is massless,
(b) pulley is massless or pulley is frictionless
Case 4 : String having mass
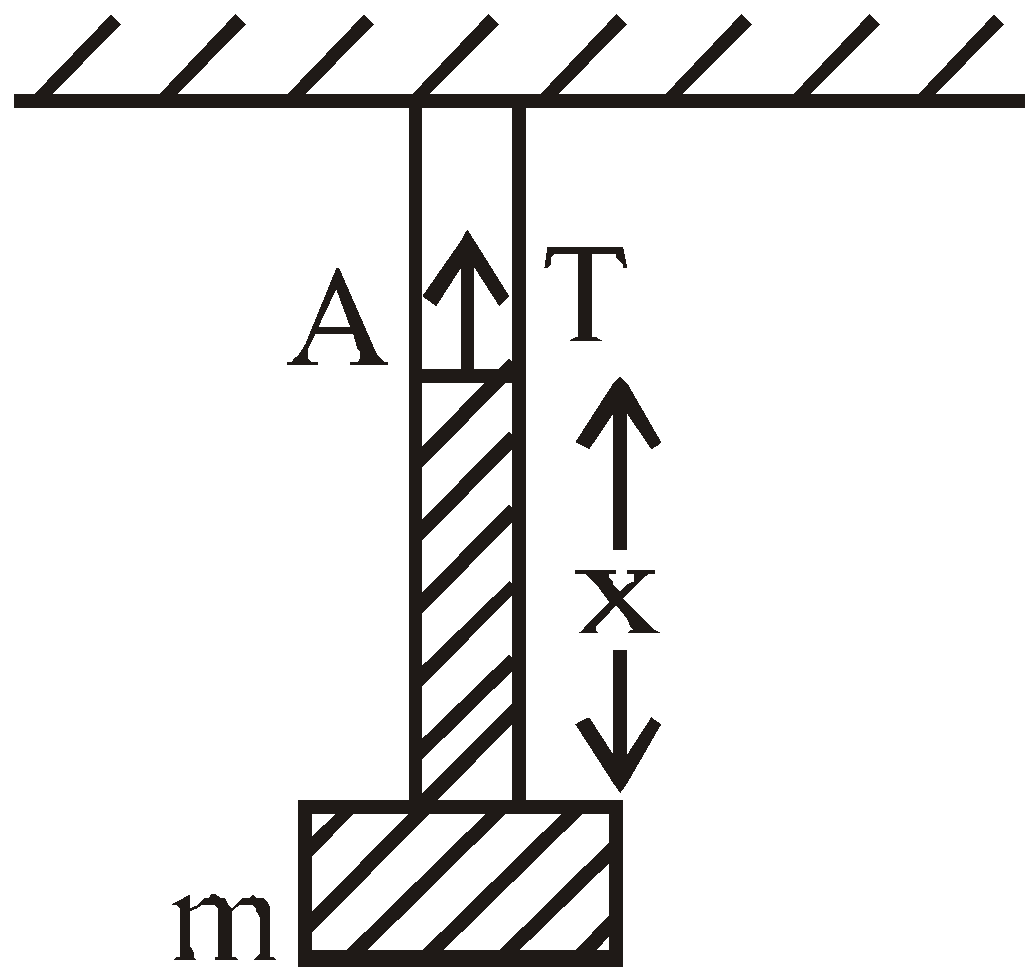
Let the total mass of the string be M and length be L. Then mass per unit length is 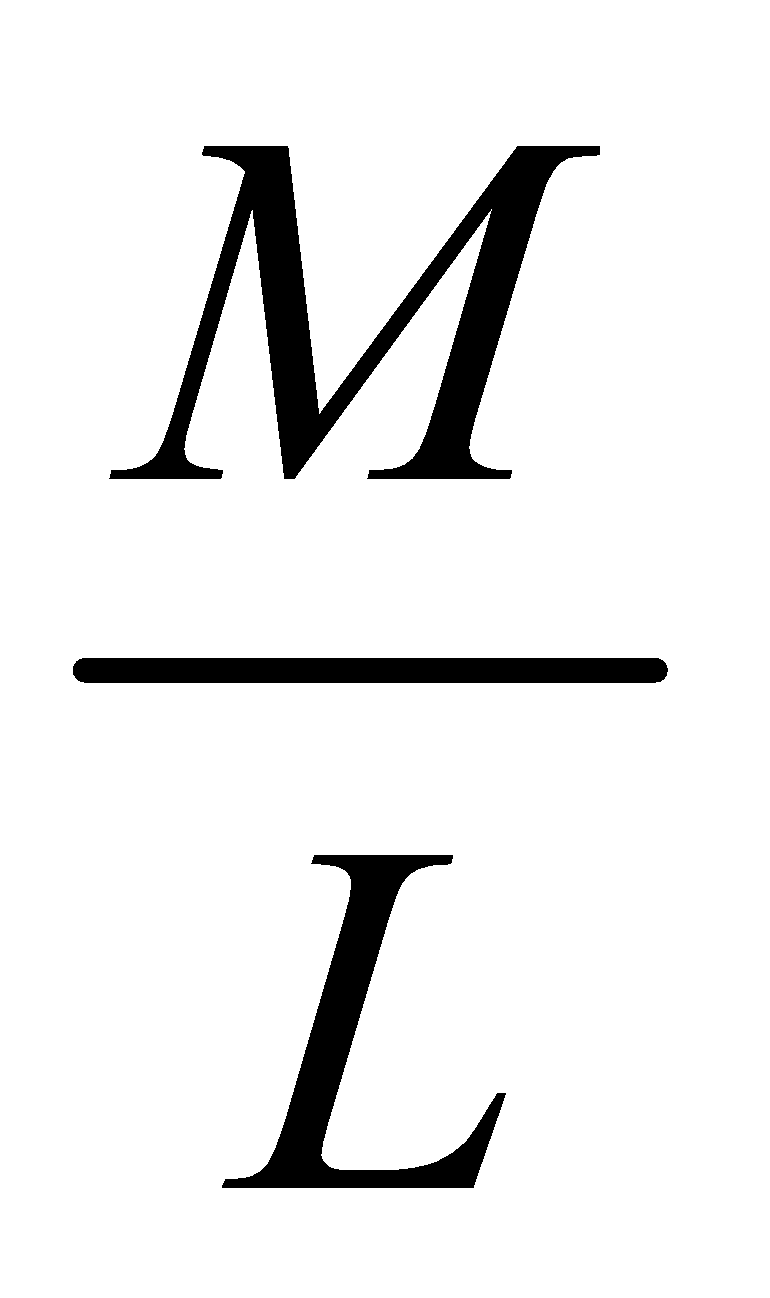
Let x be the distance of the string from the mass m. Then the mass of the shaded portion of string is 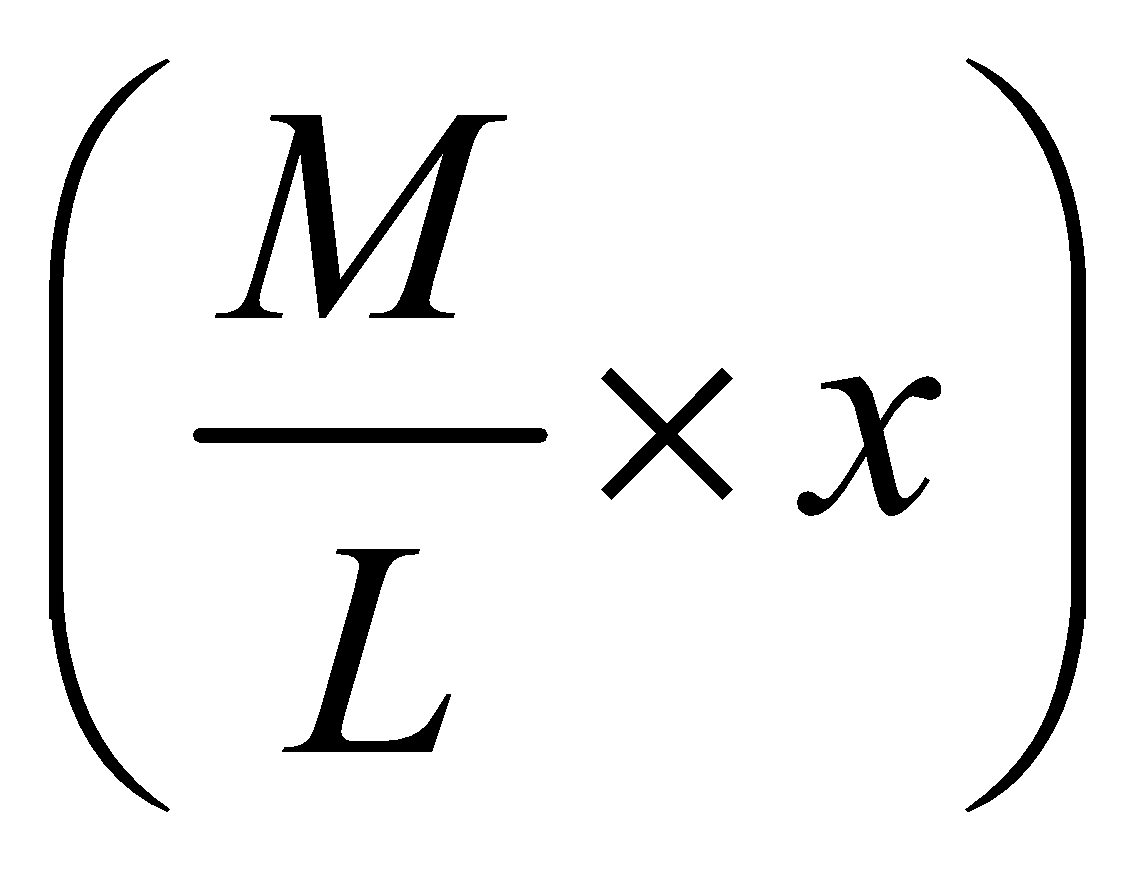
If the string is at rest then the tension T has to balance the wt of shaded portion of string and weight of mass m.
⇒ as x increases, the tension increases. Thus tension is non-uniform in a string having mass.
NORMAL FORCE
It measures how strongly one body presses the other body in contact. It acts normal to the surface of contact.
Case 1 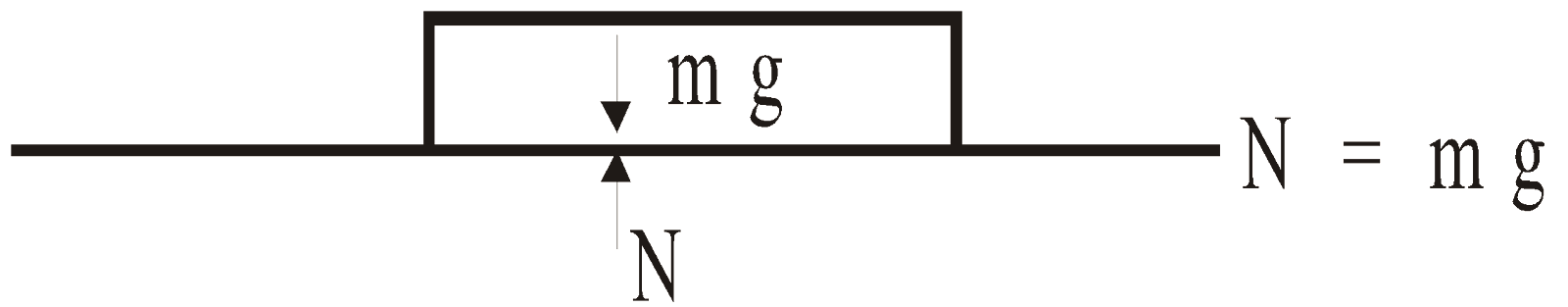
Case 2 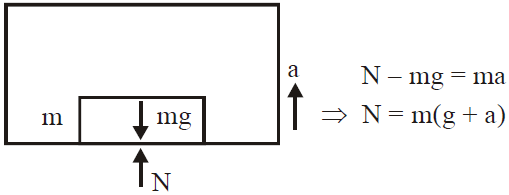

Case 3 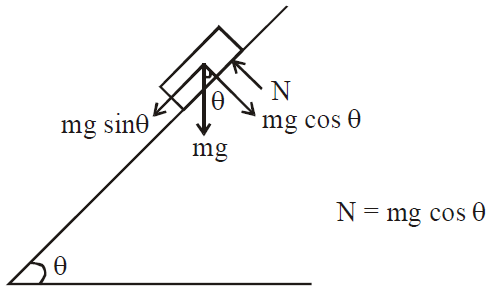
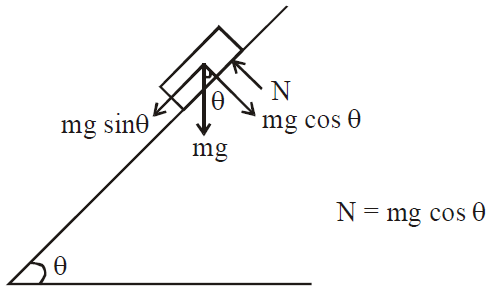
SPRING FORCE
If an object is connected by spring and spring is stretched or compressed by a distance x, then restoring force on the object F = – kx
where k is a spring contact on force constant.
FRICTIONAL FORCE
It is a force which opposes relative motion between the surfaces in contact. f = μN
This will be discussed in detail in later section.
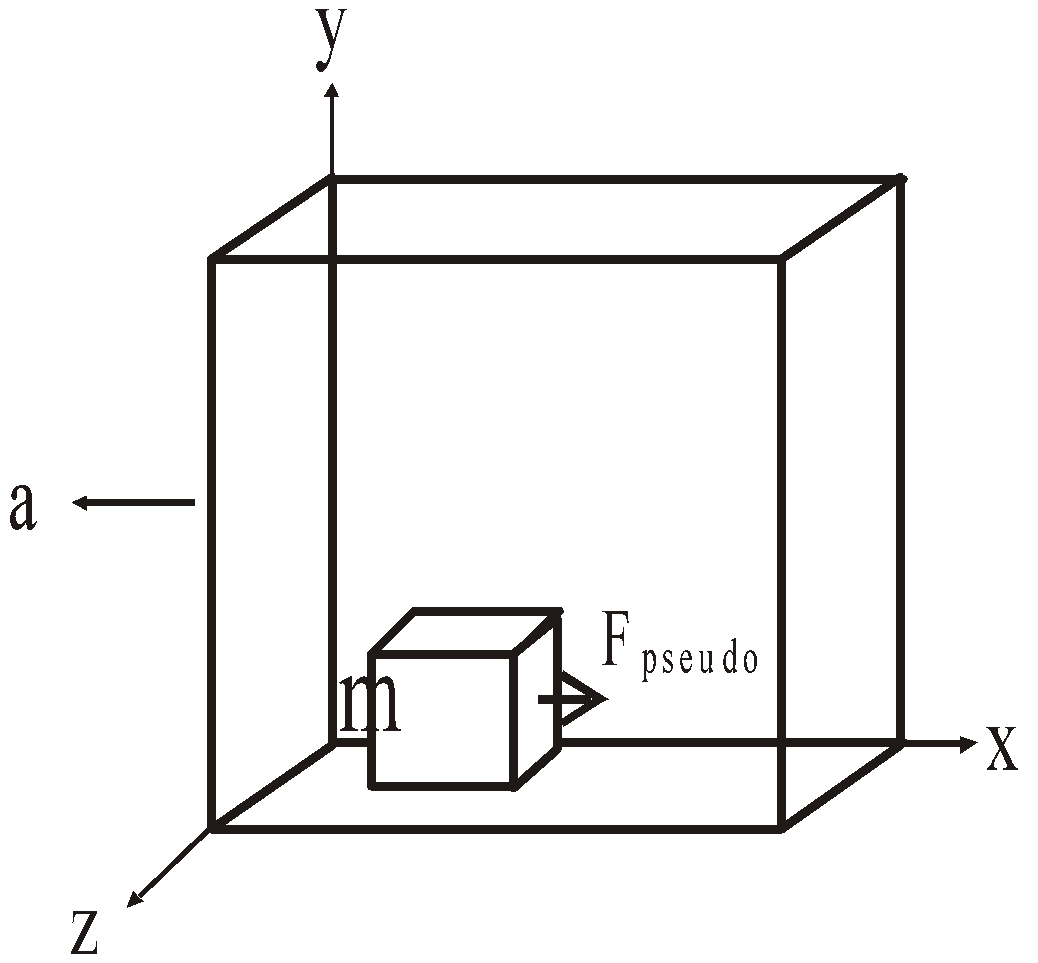
PSEUDO FORCE
If a body of mass m is placed in a non-inertial frame having acceleration  , then it experiences a Pseudo force acting in a direction opposite to the direction of
, then it experiences a Pseudo force acting in a direction opposite to the direction of  .
.
Negative sign shows that the pseudo force is always directed in a direction opposite to the direction of the acceleration of the frame.
Resultant Force
When two forces, \(\vec{F_1}\) and \(\vec{F_2}\) ,act on a body at the same point, the combined effect of these two forces is the same as the effect of a single force, called the resultant force.
The resultant force, \(\vec{R}\),is given by \(\vec{R} =\vec{F_1} +\vec{F_2} \)
CONSTRAINT MOTION
When the motion of one body is dependent on the other body, the relationship of displacements, velocities and accelerations of the two bodies are called constraint relationships.
Case 1 Pulley string system :
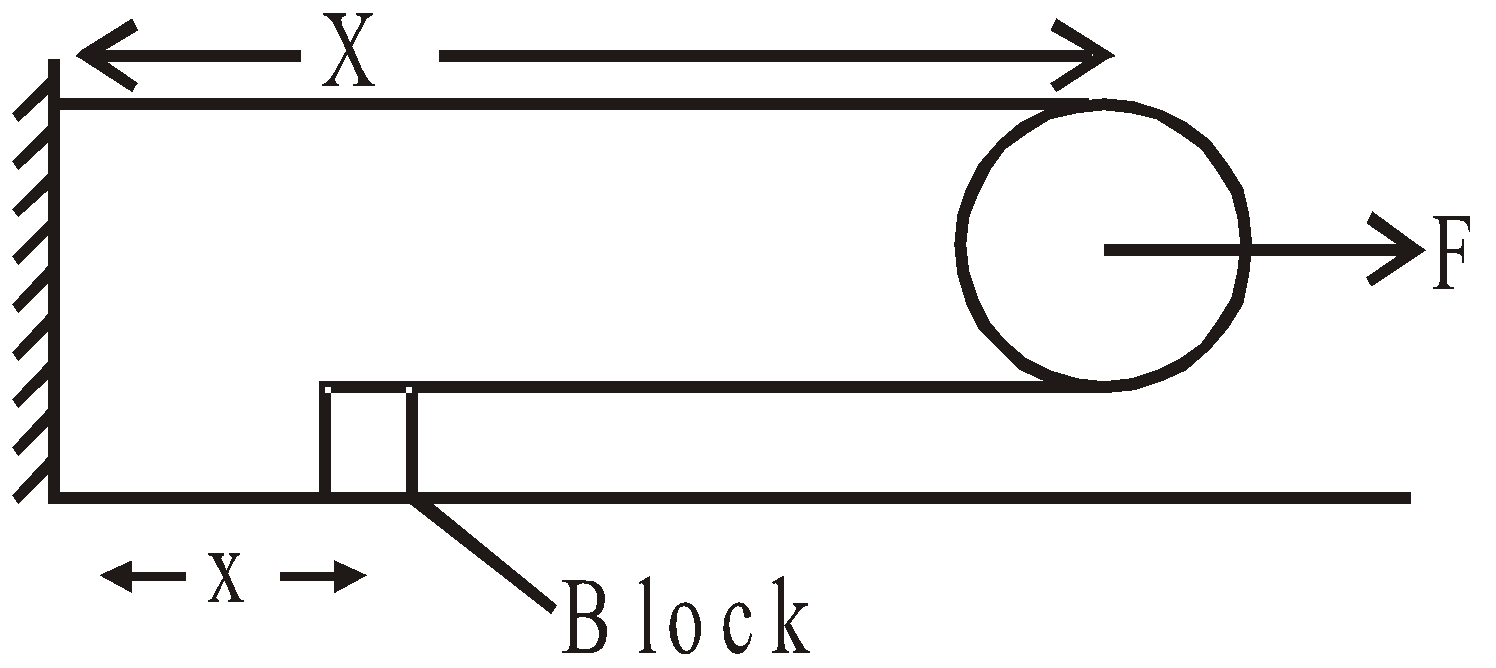
Step 1 : Find the distance of the two bodies from fixed points.
Step 2 : The length of the string remain constant. (We use of this condition)
Therefore X + (X – x) = constant ⇒ 2X – x = constant
Again differentiating we get, 2ap = aB
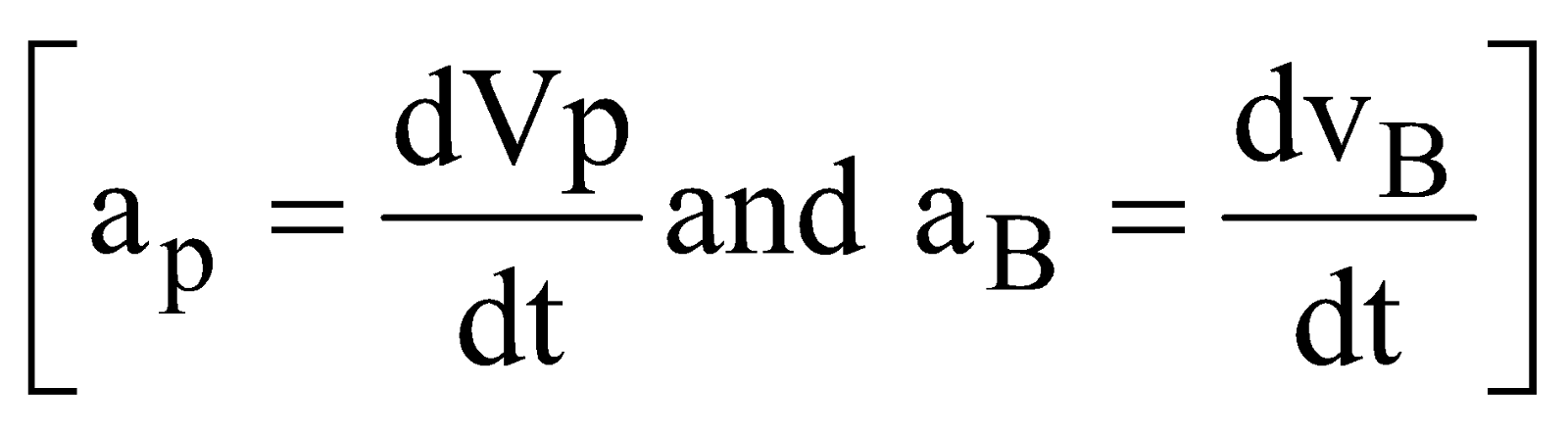
ap = acceleration of pulley, aB = acceleration of block
Case 2 Here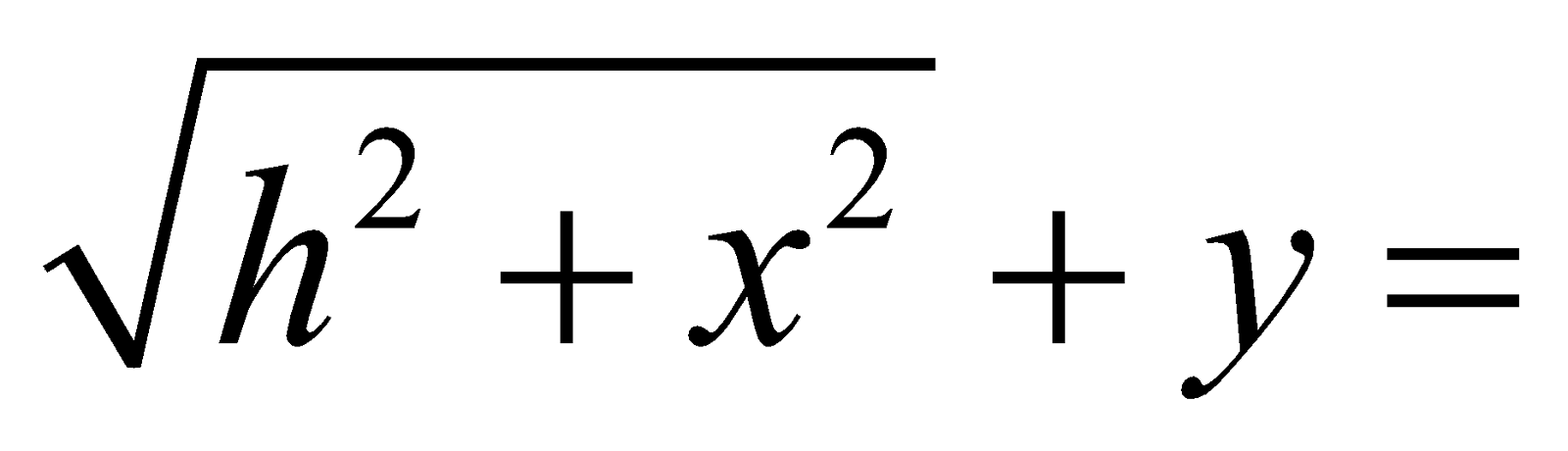 const. On differentiating w.r.t ‘t’
const. On differentiating w.r.t ‘t’
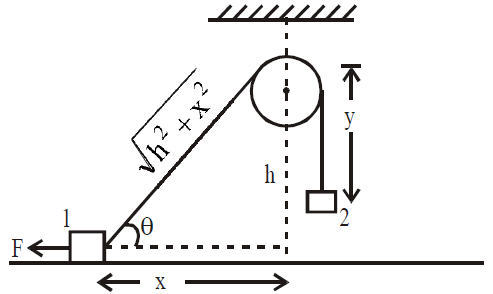
[Negative sign with dy/dt shows that with increase in time, y decreases]
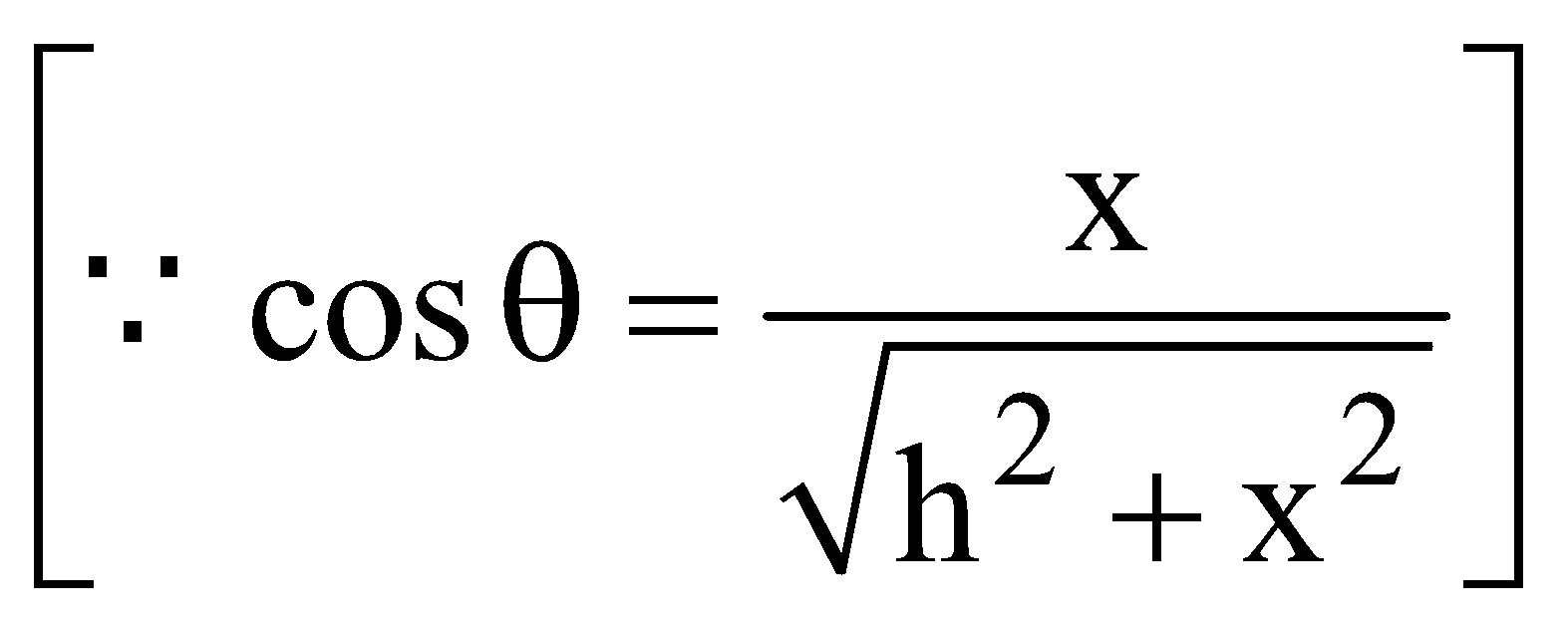
Case 3 Wedge block system : Thin lines represents the condition of wedge block at t = 0 and dotted lines at t = t
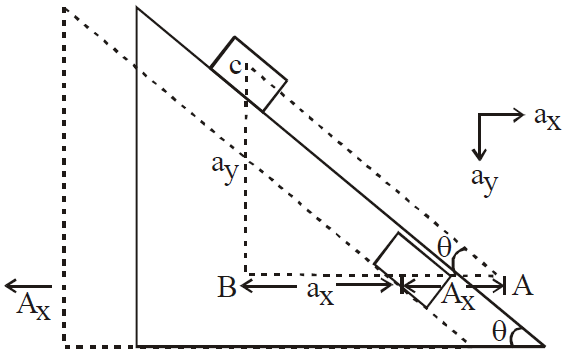
Ax = acceleration of wedge towards left
ax, ay = acceleration of block as shown
From Δ ABC , 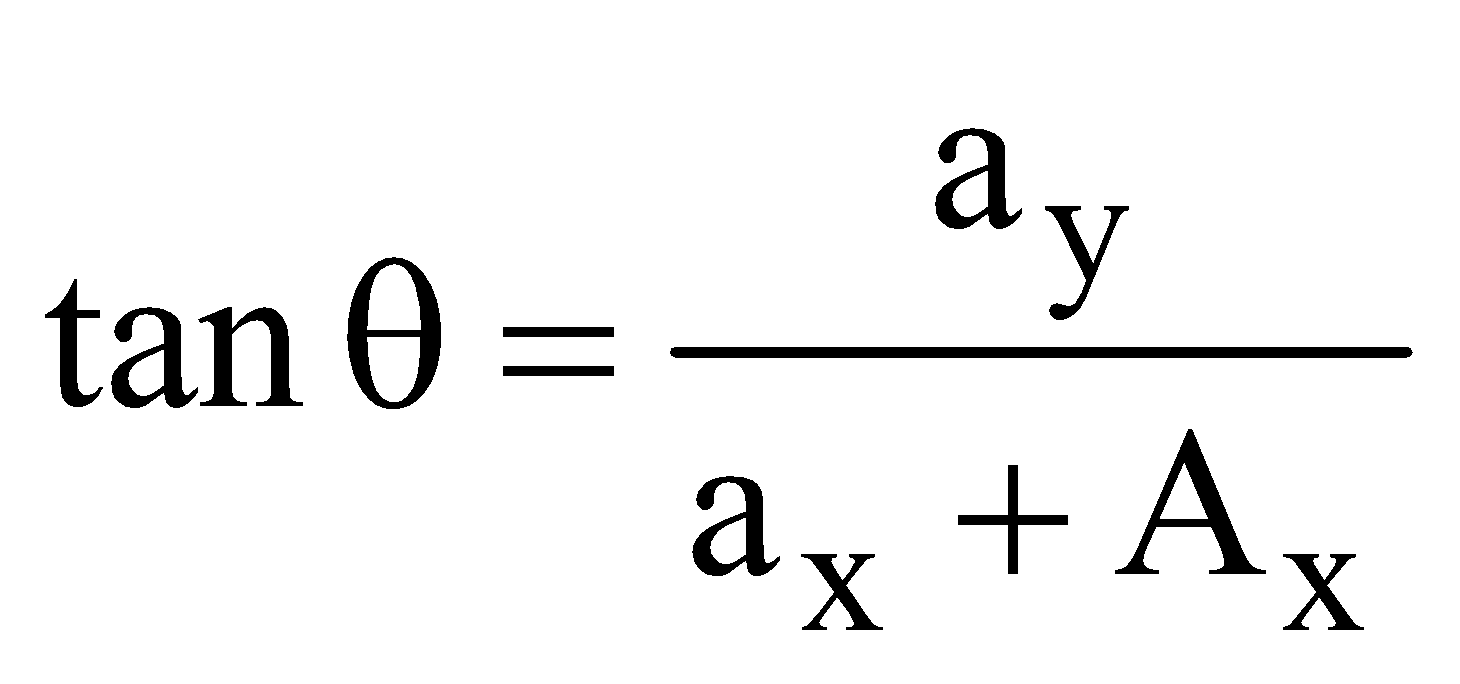
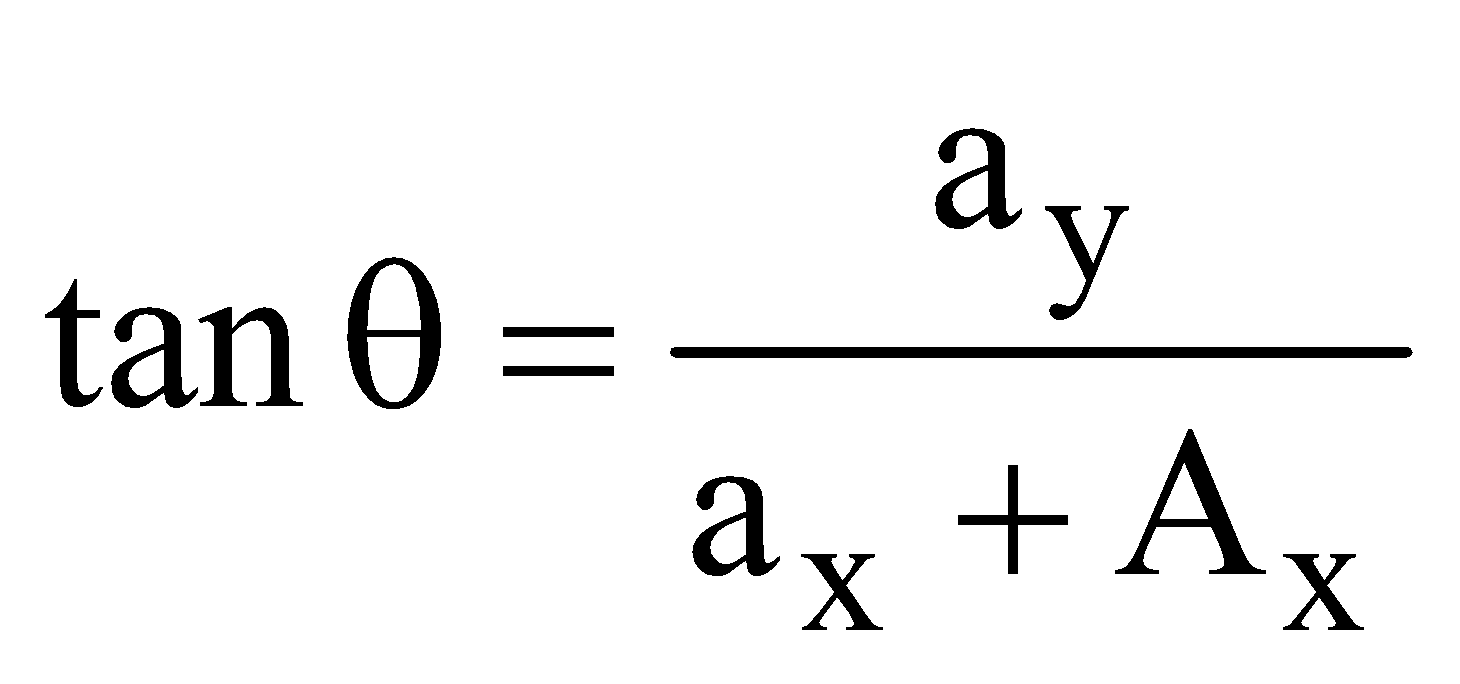
FRAME OF REFERENCE
Reference frames are coordinate systems in which an event is described.
There are two types of reference frames
- Inertial frame of reference: These are frames of reference in which Newton’s laws hold good. These frames are at rest with each other or which are moving with uniform speed with respect to each other. All reference frames present on surface of Earth are supposed to be inertial frame of reference.
- Non – inertial frame of reference: Newton’s law do not hold good in non-inertial reference frame.
- All accelerated and rotatory reference frames are non – inertial frame of reference. Earth is a non-inertial frame.
Note:- When the observer is in non-inertial reference frame a pseudo force is applied on the body under observation.
FREE BODY DIAGRAM (FBD)
Free body diagram of a mass is a separate diagram of that mass. All forces acting on the mass are sketched. A FBD is drawn to visualise the direct forces acting on a body.
Case 1 : Masses M1 and M2 are tied to a string, which goes over a frictionless pulley
- If M2 > M1 and they move with acceleration a
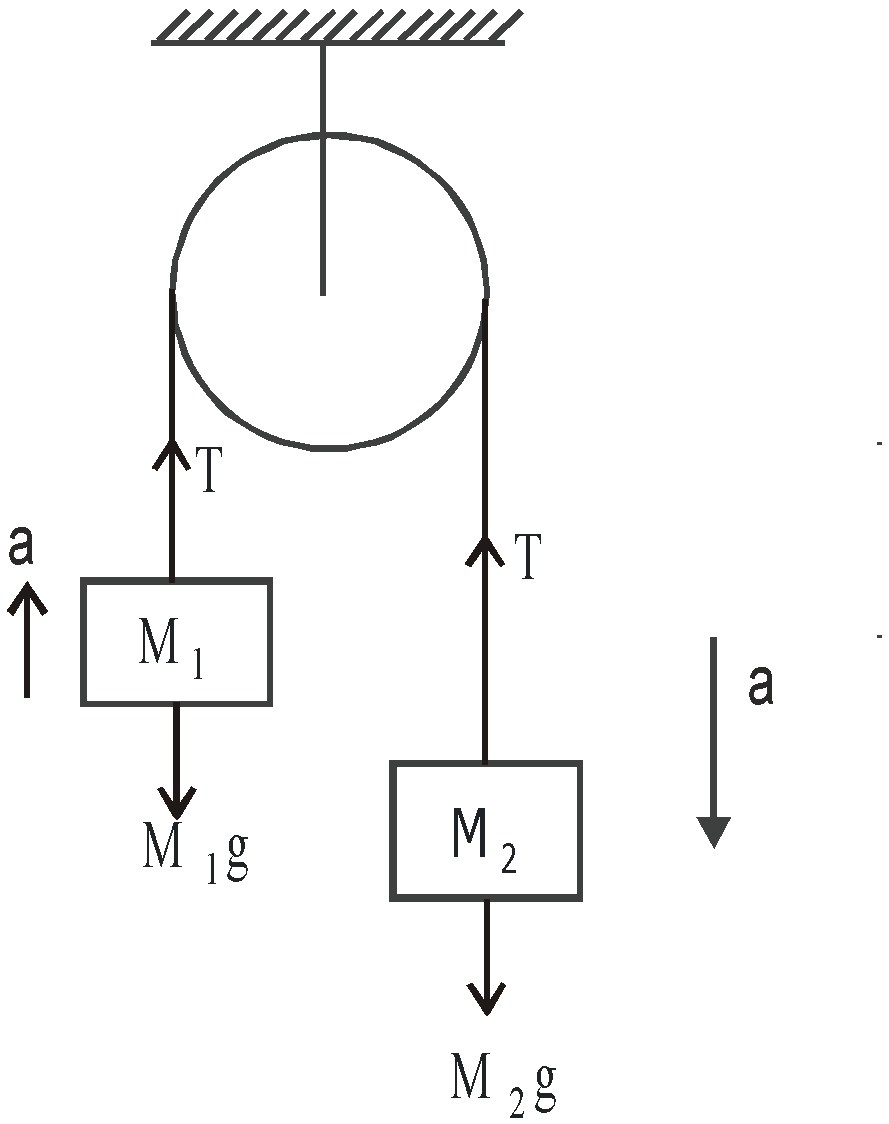
FBD of M1, FBD of M2
where T is the tension in the string.
It gives 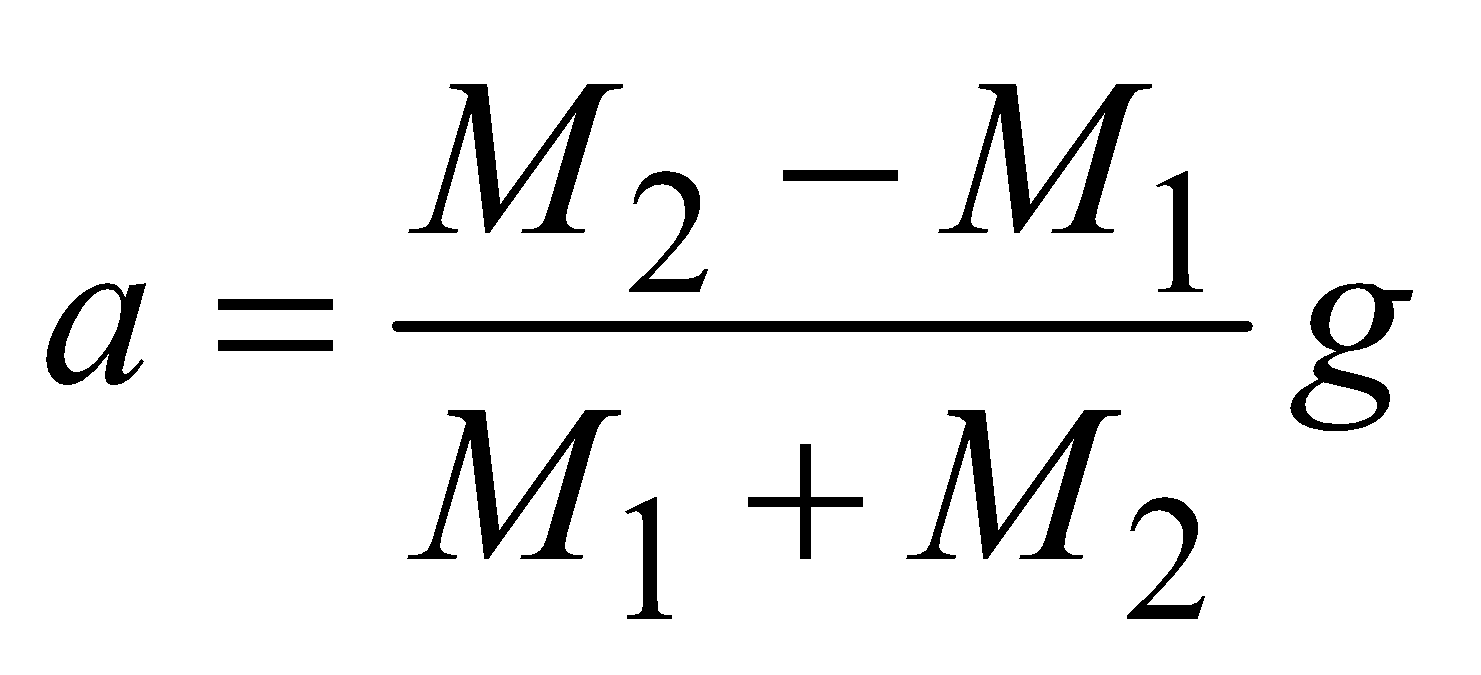 and
and 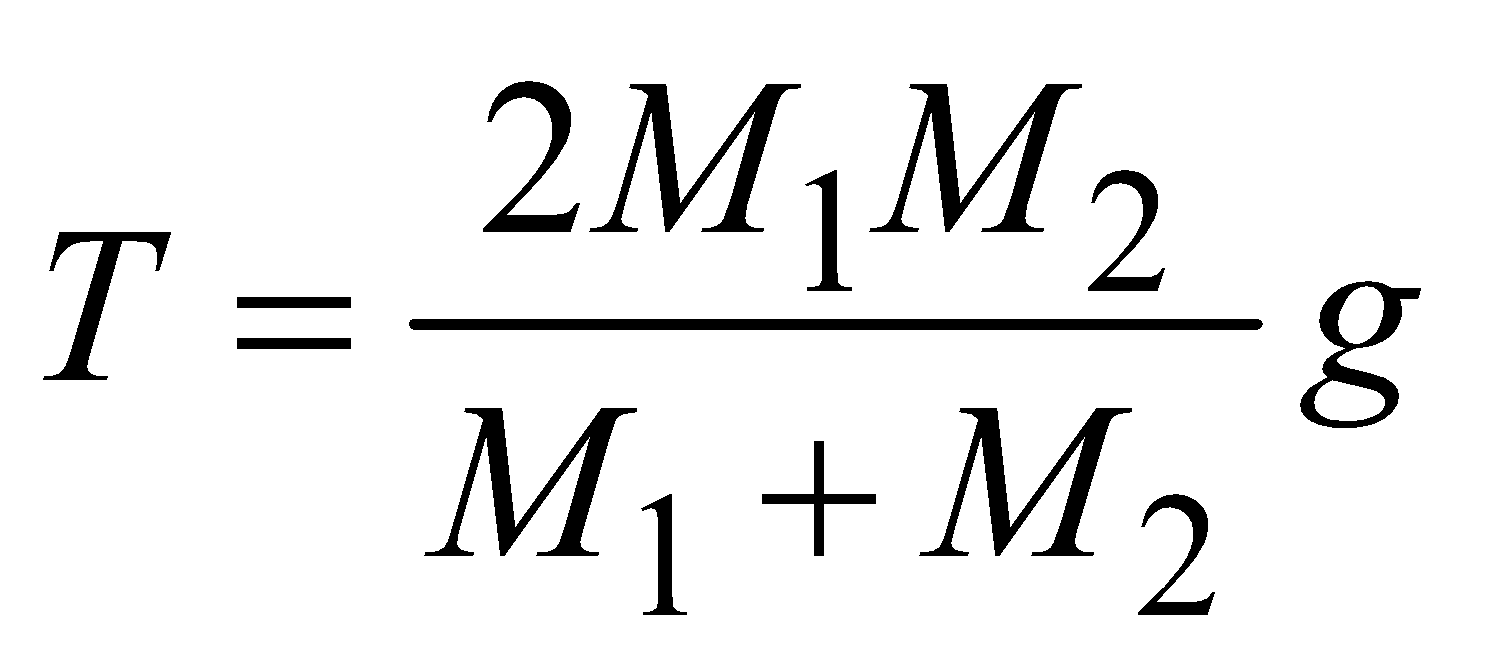
- If the pulley begins to move with acceleration f, downwards
Case 2 : Three masses M1, M2 and M3 are connected with strings as shown in the figure and lie on a frictionless surface. They are pulled with a force F attached to M1.
The forces on M2 and M3 are as follows
Acceleration of the system is 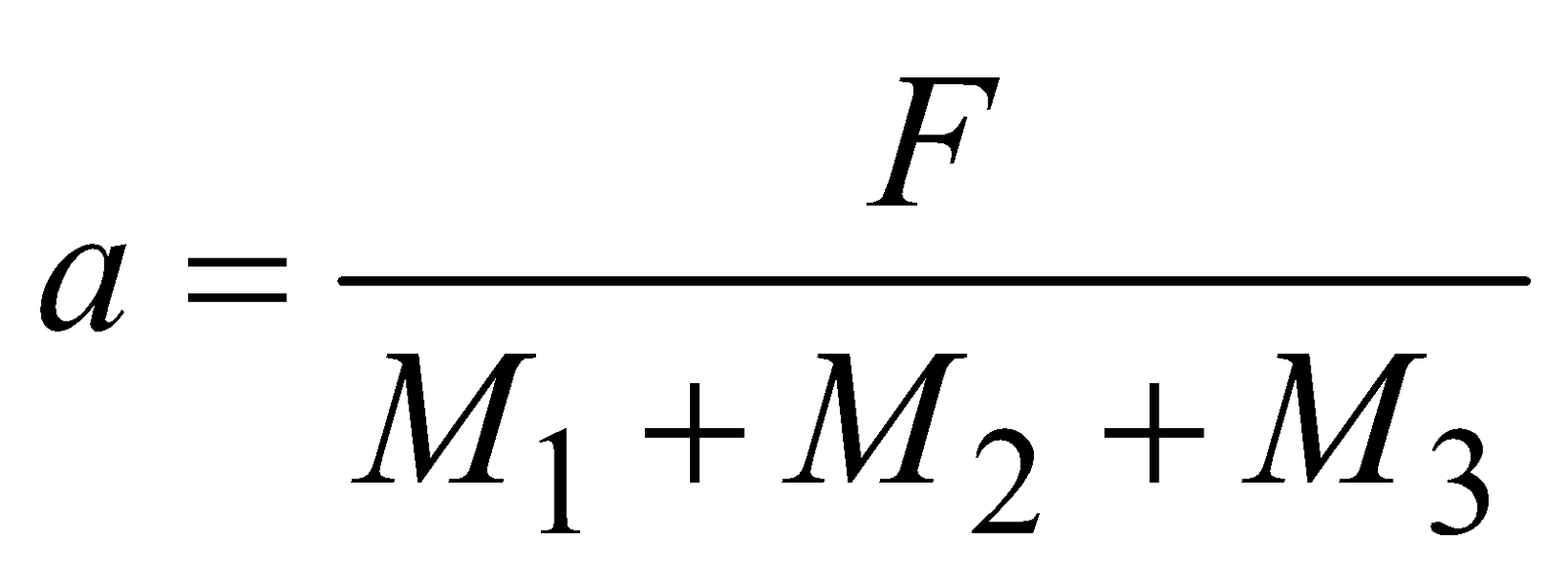
Case 3 : Two blocks of masses M1 and M2 are suspended vertically from a rigid support with the help of strings as shown in the figure. The mass M2 is pulled down with a force F.
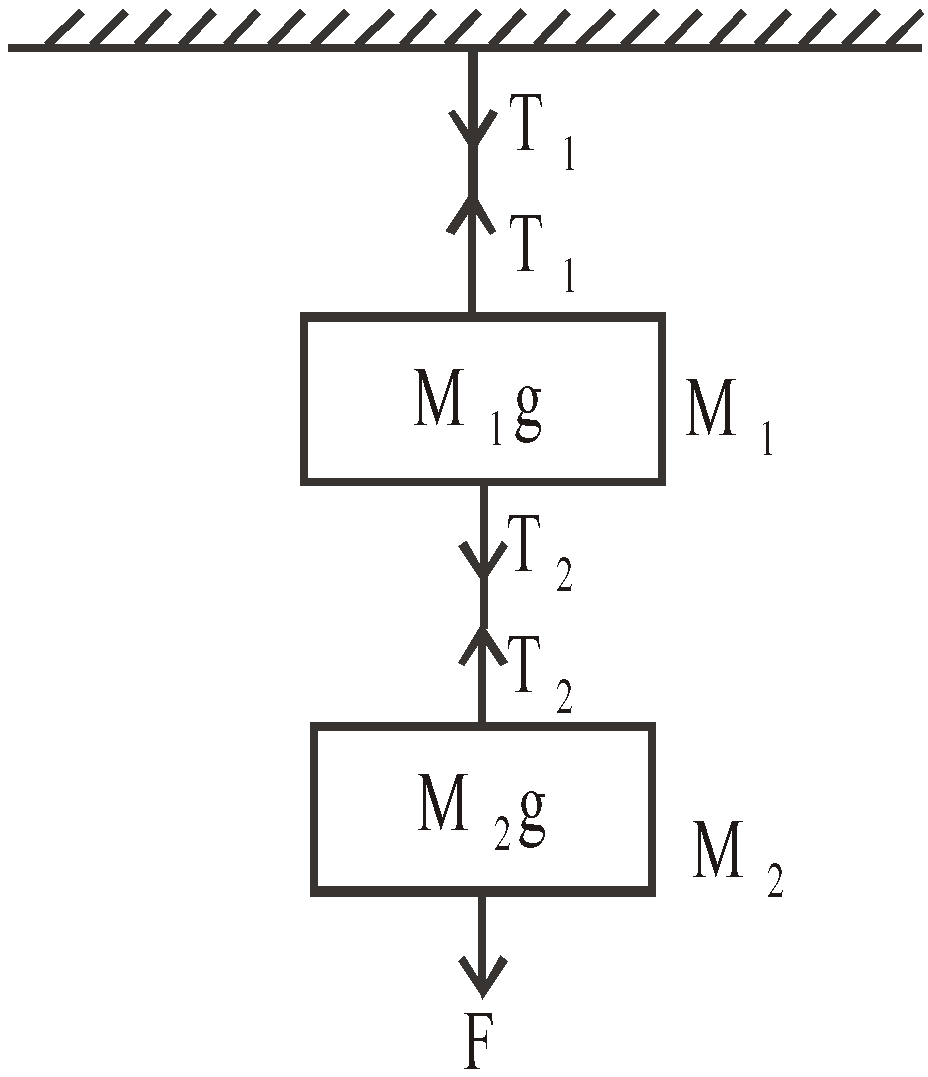
The tension between the masses M1 and M2 will be T2 = F + M2g
Tension between the support and the mass M1 will be T1 = F + (M1 + M2)g
Case 4 : Two masses M1 and M2 are attached to a string which passes over a pulley attached to the edge of a horizontal table. The mass M1 lies on the frictionless surface of the table.
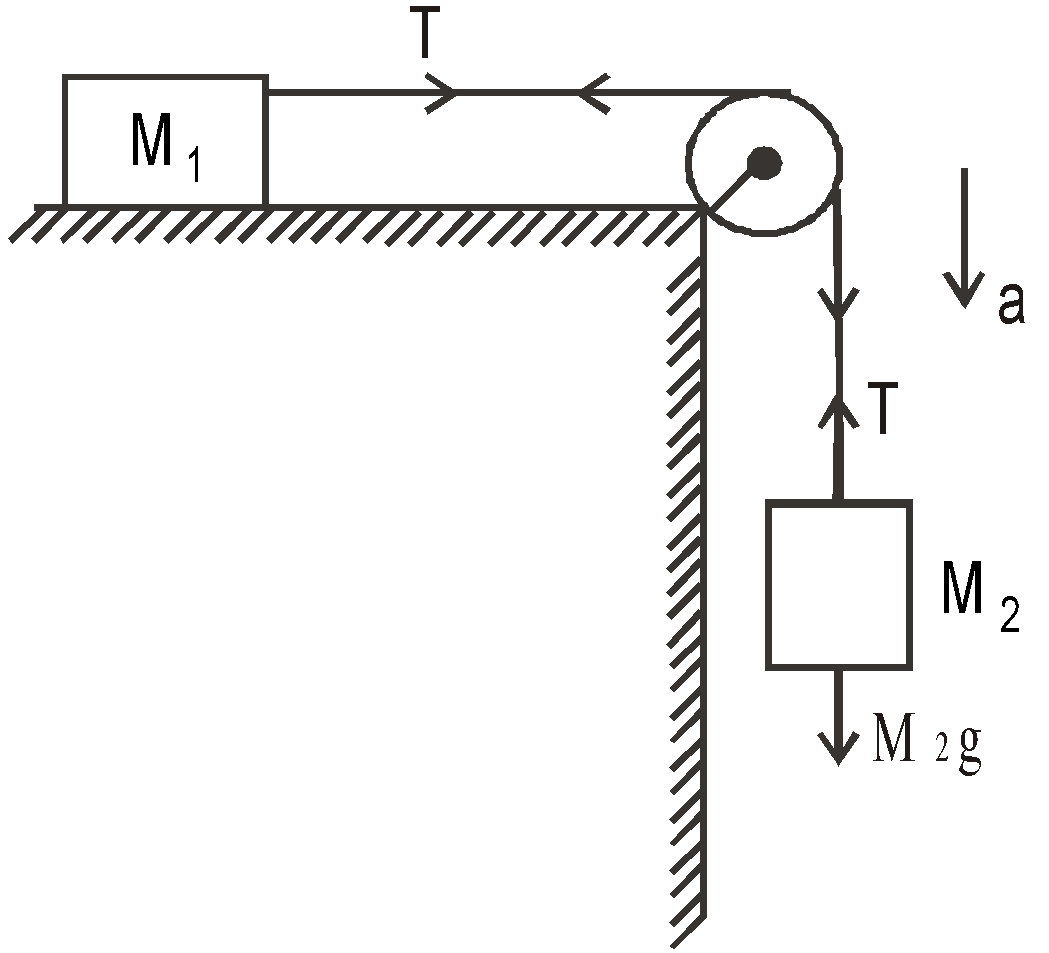
Let the tension in the string be T and the acceleration of the system be a. Then
T = M1a …(1)
M2g – T = M2a …(2)
Adding eqns. (1) and (2), we get
Case 5 : Two masses M1 and M2 are attached to the ends of a string, which passes over a frictionless pulley at the top of the inclined plane of inclination θ. Let the tension in the string be T.
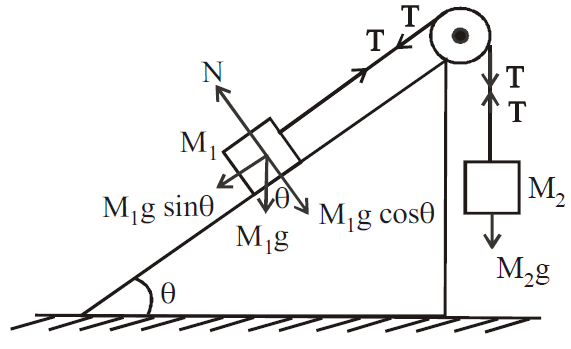
- When the mass M1 moves upwards with acceleration a.
From the FBD of M1 and M2,
T – M1g sin θ = M1a …(1)
M2g – T = M2a …(2)
Solving eqns. (1) and (2) we get,
FBD of mass M1 

- When the mass M1 moves downwards with acceleration a.
Equation of motion for M1 and M2,
M1g sin θ – T = M1a …(1)
T – M2g = M2a …(2)
Solving eqns. (1) and (2) we get,
- If (M2/M1 = sinθ) then the system does not accelerate.
- Changing position of masses, does not affect the tension. Also, the acceleration of the system remains unchanged.
- If M1 = M2 = M (say), then
Case 6 : Two masses M1 and M2 are attached to the ends of a string over a pulley attached to the top of a double inclined plane of angle of inclination α and β.
Let M2 move downwards with acceleration a and the tension in the string be T then
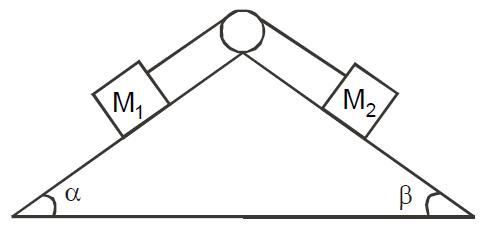
FBD of M1
Equation of motion for M1
T – M1g sin α = M1a
or T = M1g sin α + M1a …(1)
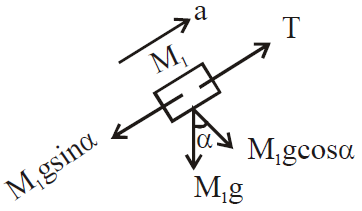
FBD of M2
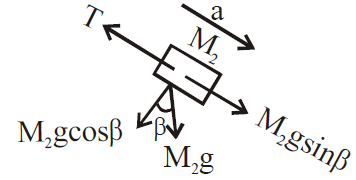
Equation of motion for M2
M2g sinβ – T = M2a
or T = M2g sin β – M2a …(2)
Using eqn. (1) and (2) we get,
M1g sin α + M1a = M2g sin β – M2a
Solving we get,
Case 7 : A person/monkey climbing a rope
- A person of mass M climbs up a rope with acceleration a. The tension in the rope will be M(g+a).
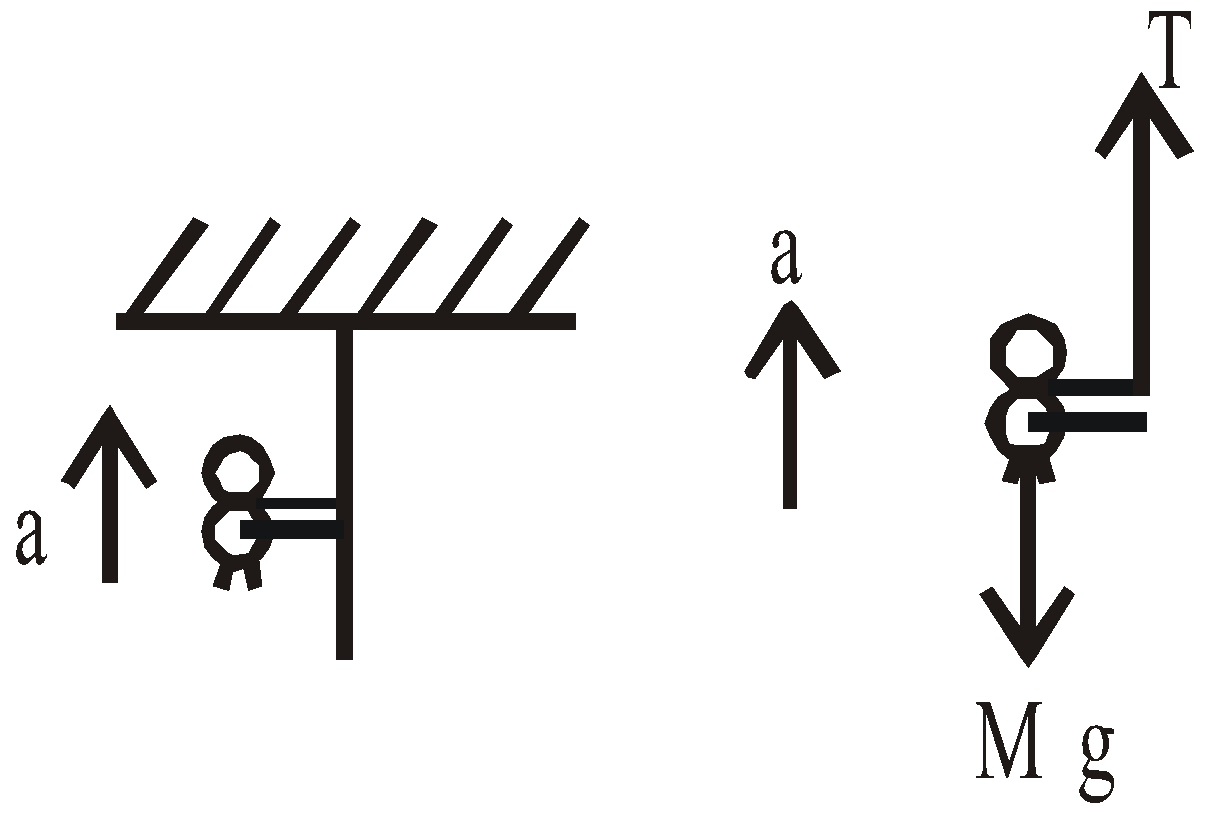
T – Mg = Ma ⇒ T = M(g + a)
- If the person climbs down along the rope with acceleration a, the tension in the rope will be M(g–a).
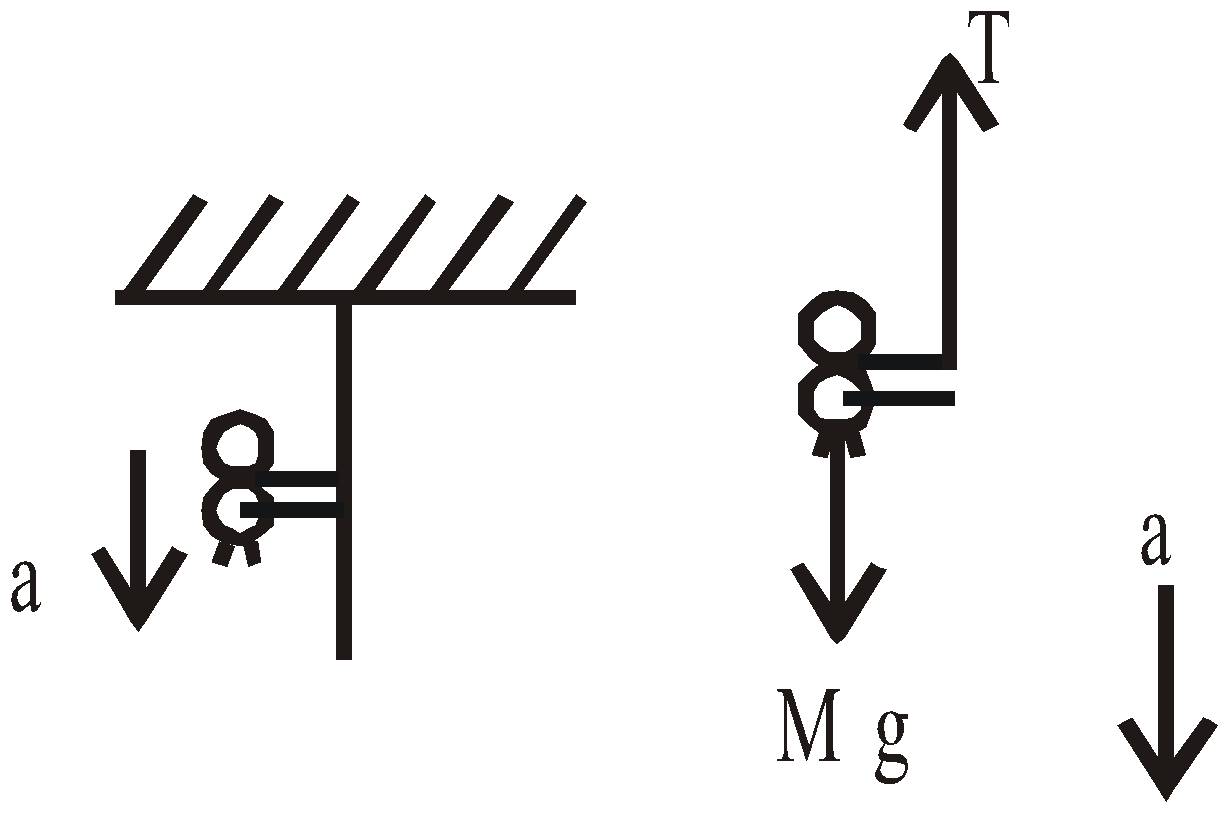
Mg – T = Ma ⇒ T = M(g – a)
- When the person climbs up or down with uniform speed, tension in the string will be Mg.
Case 8 : A body starting from rest moves along a smooth inclined plane of length l, height h and having angle of inclination θ.
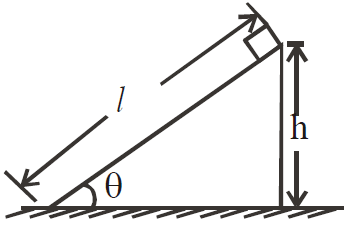 FBD of body
FBD of body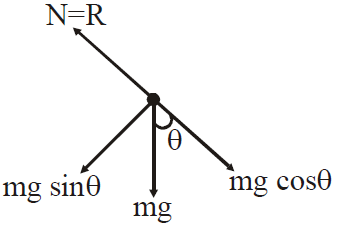
(where N=R is normal reaction applied by plane on the body of mass m)
For downward motion, along the inclined plane,
By work-energy theorem loss in P.E. = gain in K.E.
Also, from the figure, h = l sin θ. 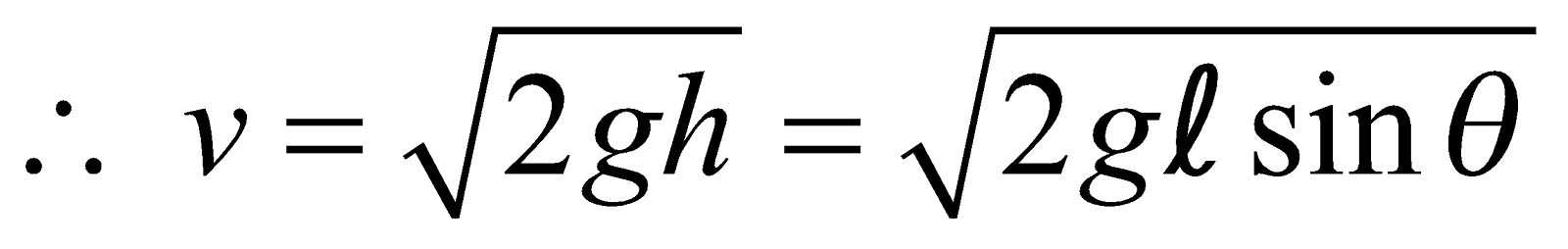
- Acceleration down the plane is g sin θ.
- Its velocity at the bottom of the inclined plane will be
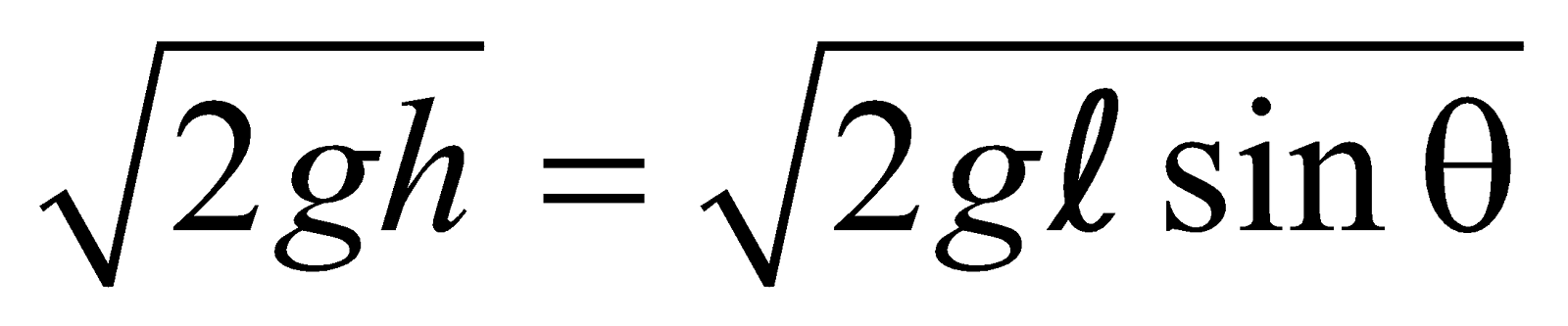
- Time taken to reach the bottom will be
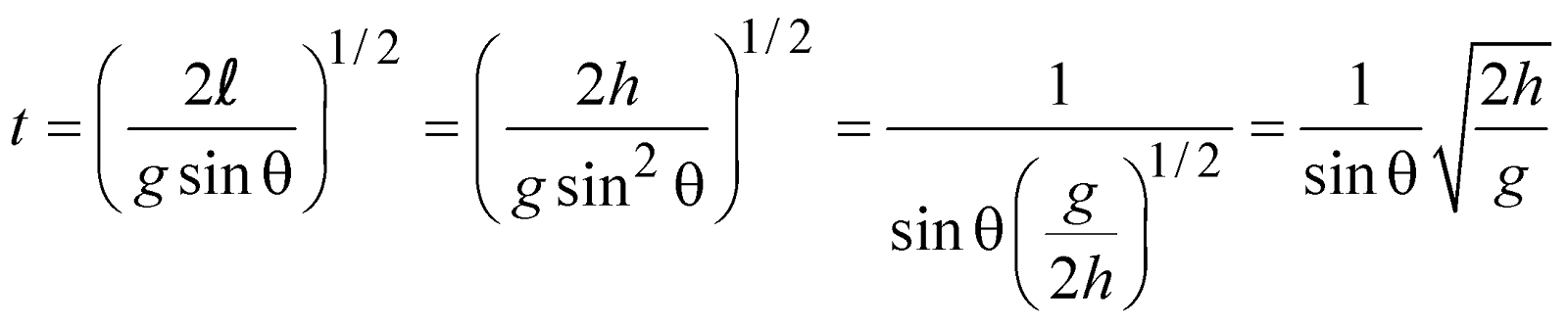
- If angles of inclination are θ1 and θ2 for two inclined planes
Keeping the length constant then 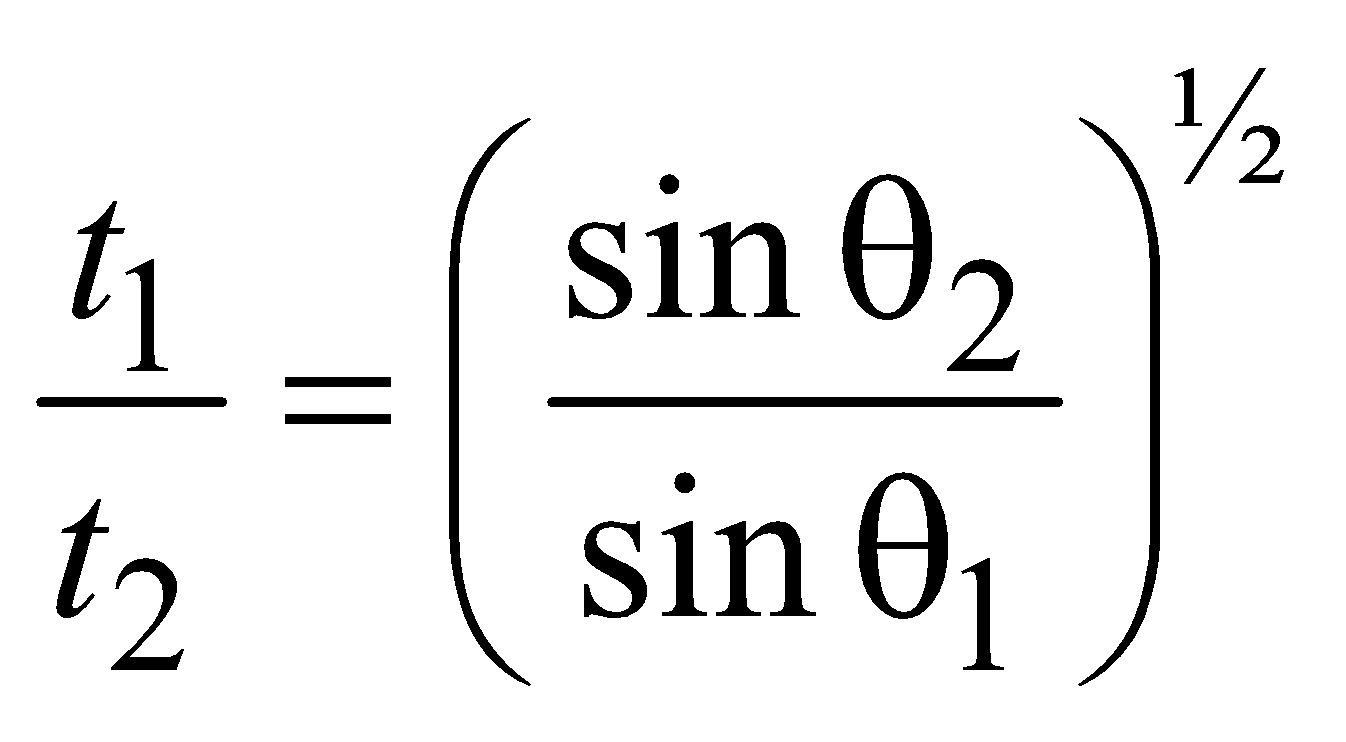
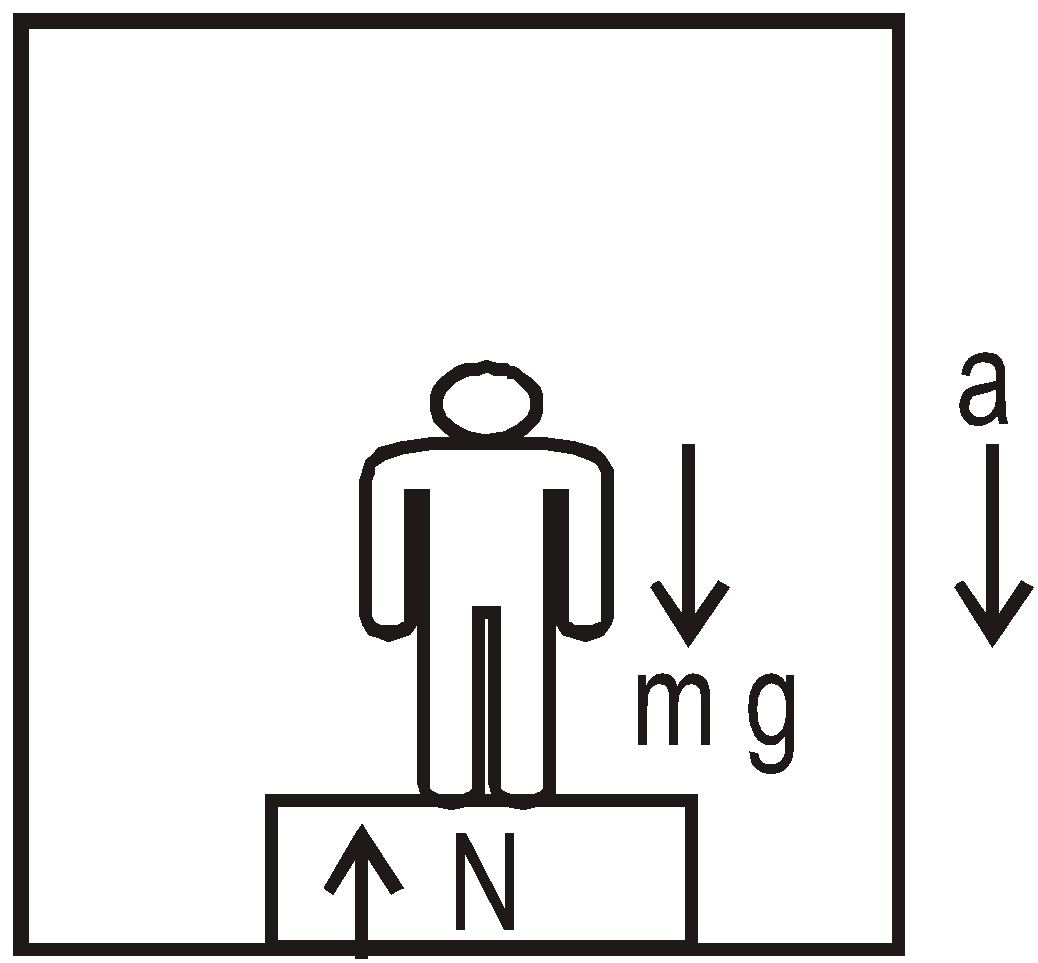
Case 9 : Weight of a man in a lift :
- When lift is accelerated upward
In this case the man also moves in upward direction with an acceleration
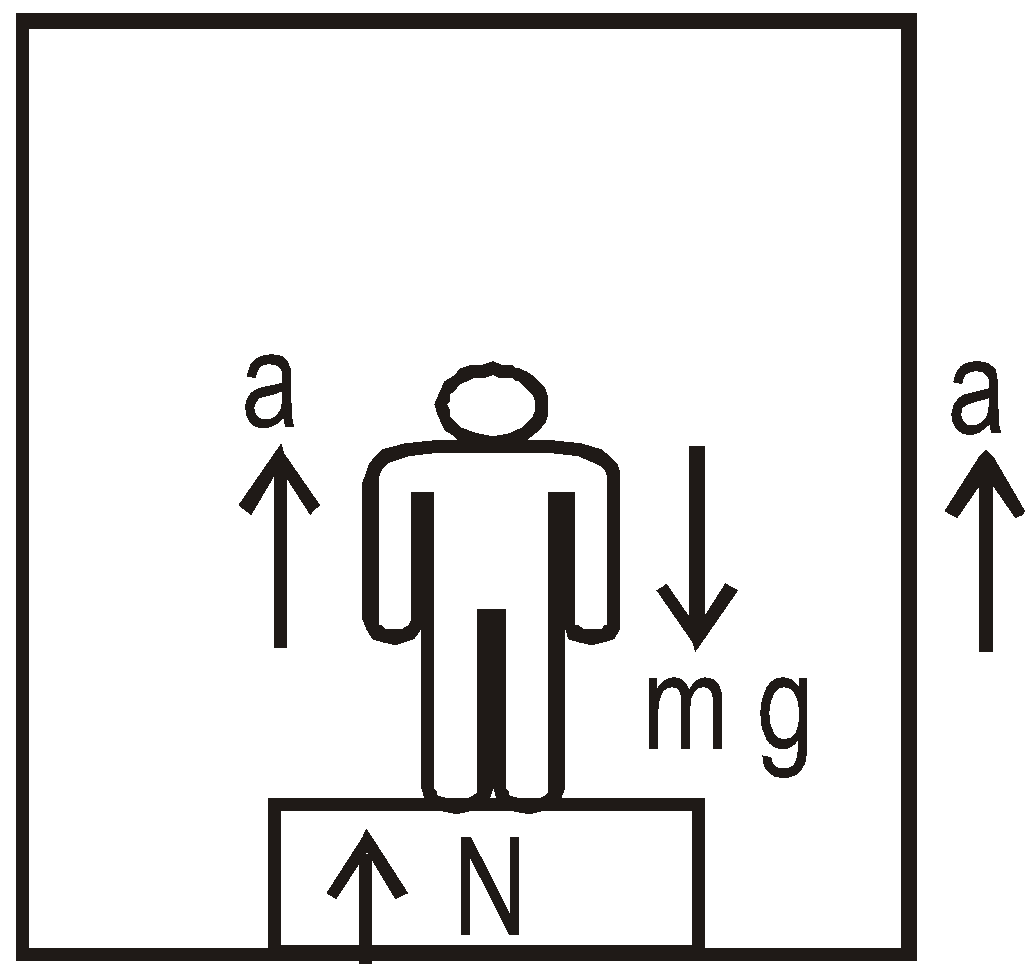
Then from Newton’ second law
N – mg = ma or N = m(g + a)
or Wapp = m(g + a) 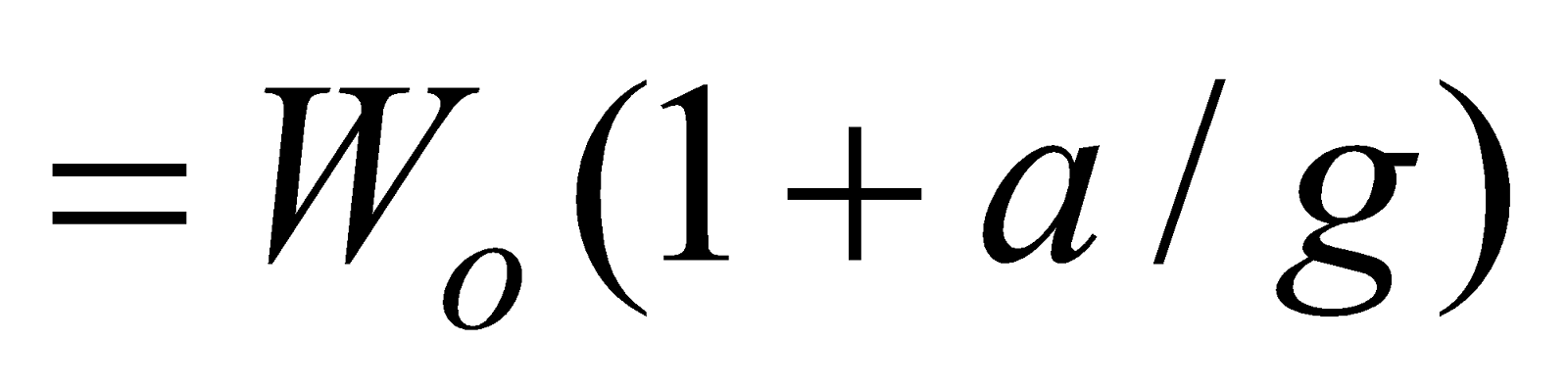 (as W = mg)
(as W = mg)
Where Wapp is apparent weight of the man in the lift, Wo is the real weight, N is the reaction of lift on the man. It is clear that N = Wapp
When the lift moves upward and if we measure the weight of the man by any means (such as spring balance) then we observe more weight (i.e., Wapp) than the real weight (Wo) Wapp >Wo
- When lift is accelerated downward
In this case from Newton’s second law
mg – N = ma
or N = m(g – a) = Wo(1– a/g)
or W’app= Wo(1– a/g) 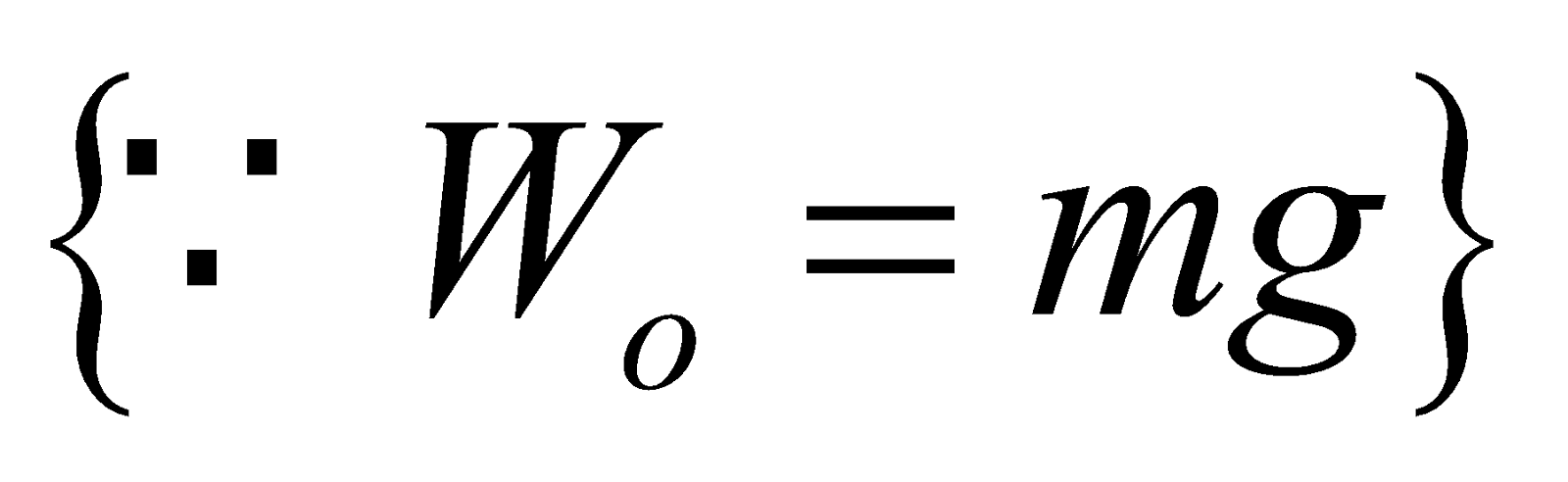
If we measure the weight of man by spring balance, we observe deficiency because Wapp< Wo.
- When lift is at rest or moving with constant velocity
From Newton’s second law
N –mg = 0 or N = mg
N –mg = 0 or N = mg
In this case spring balance gives the true weight of the man.
case 10 Acceleration of block pushing on block
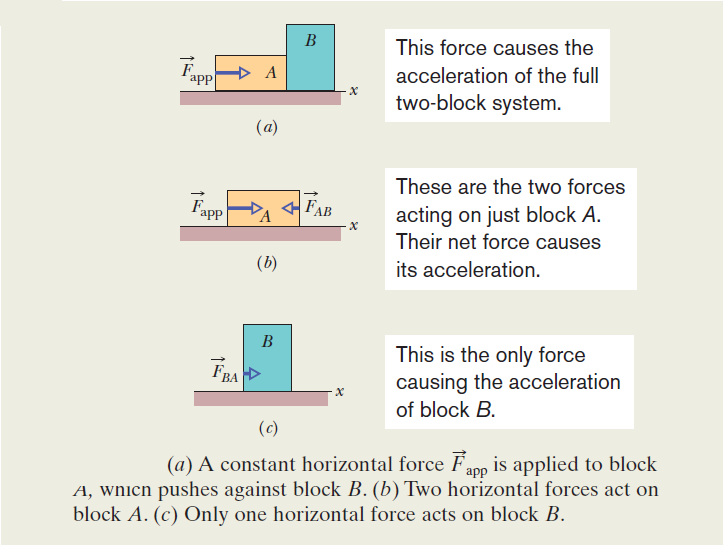
Solution:
Because of the direction in which force \( \vec{F_{app}} \) is applied, the two blocks form a rigidly connected system. We can relate the net force on the system to the acceleration of the system with Newton’s second law. Here, once again for the x axis, we can write that law as
\(F_{app} =(m_A+m_B)a\)
where now we properly apply \(F_{app}\) to the system with total mass \(m_A+m_B\). Solving for a and substituting known values, we find
\(a=\frac{F_{app}}{m_A+m_B}\)
Case 11 : Three masses M1, M2 and M3 are placed on a smooth surface in contact with each other as shown in the figure. A force F pushes them as shown in the figure and the three masses move with acceleration a,
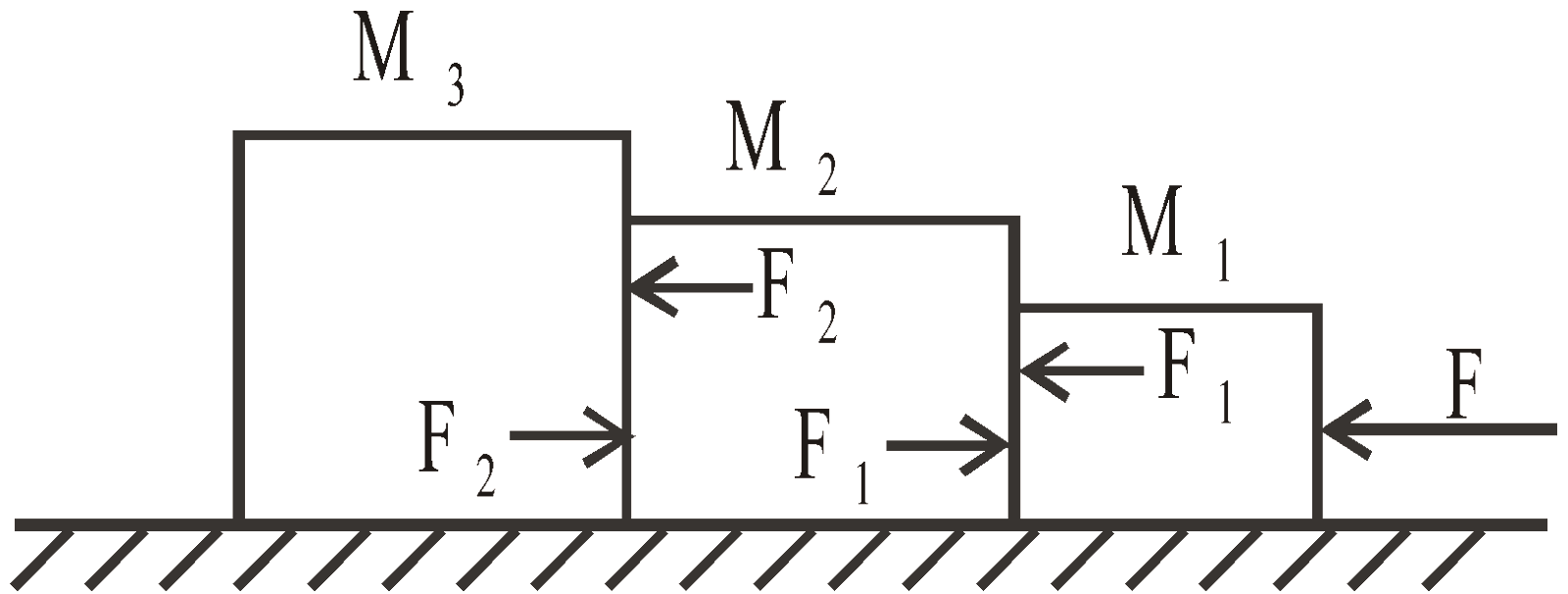
Adding eqns. (i), (ii) and (iii) we get, 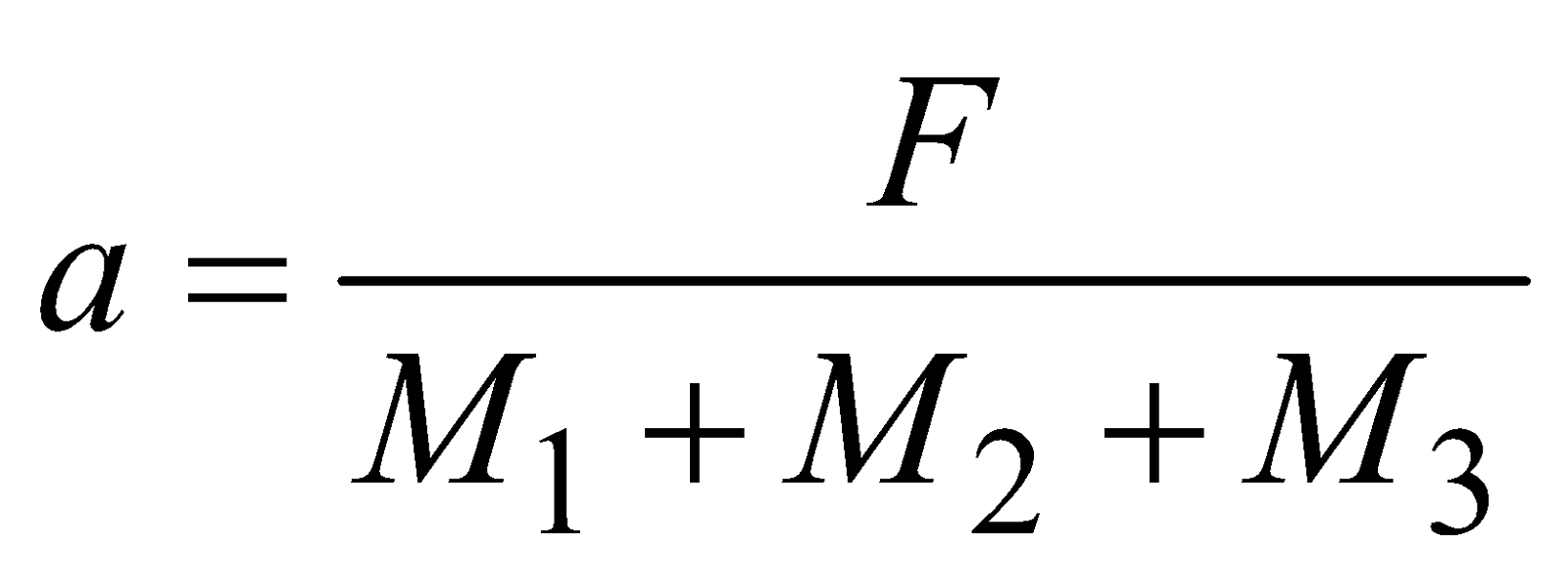
⇒ 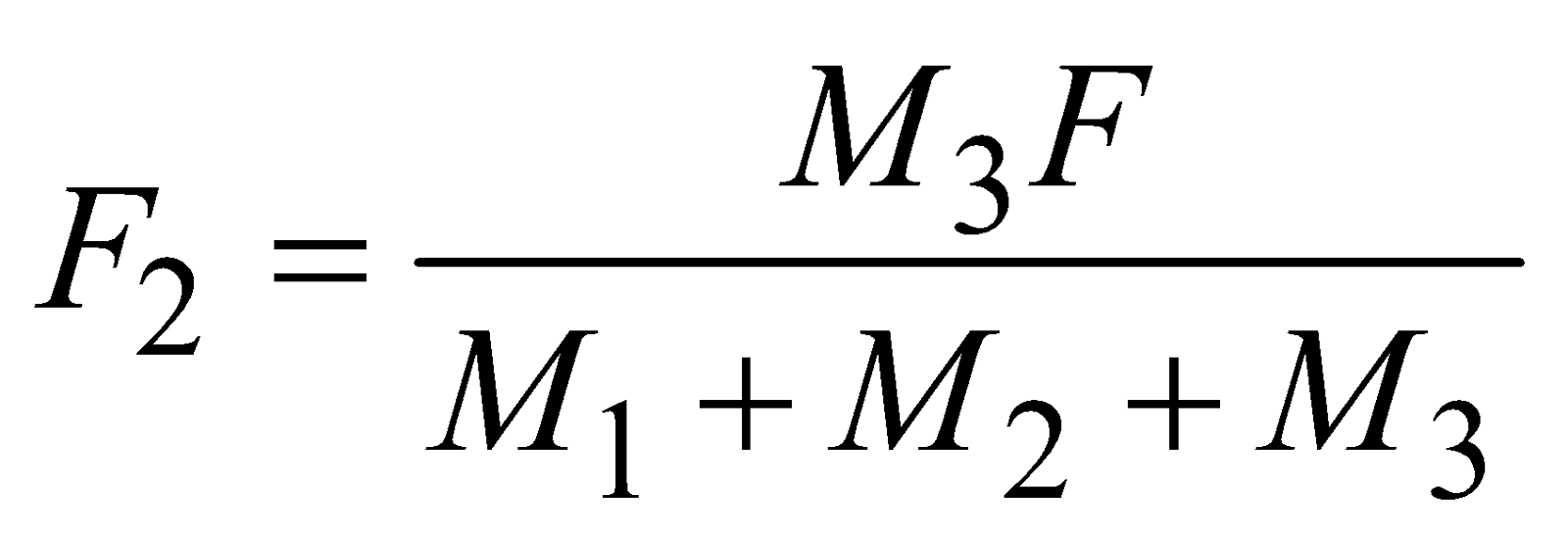 and
and 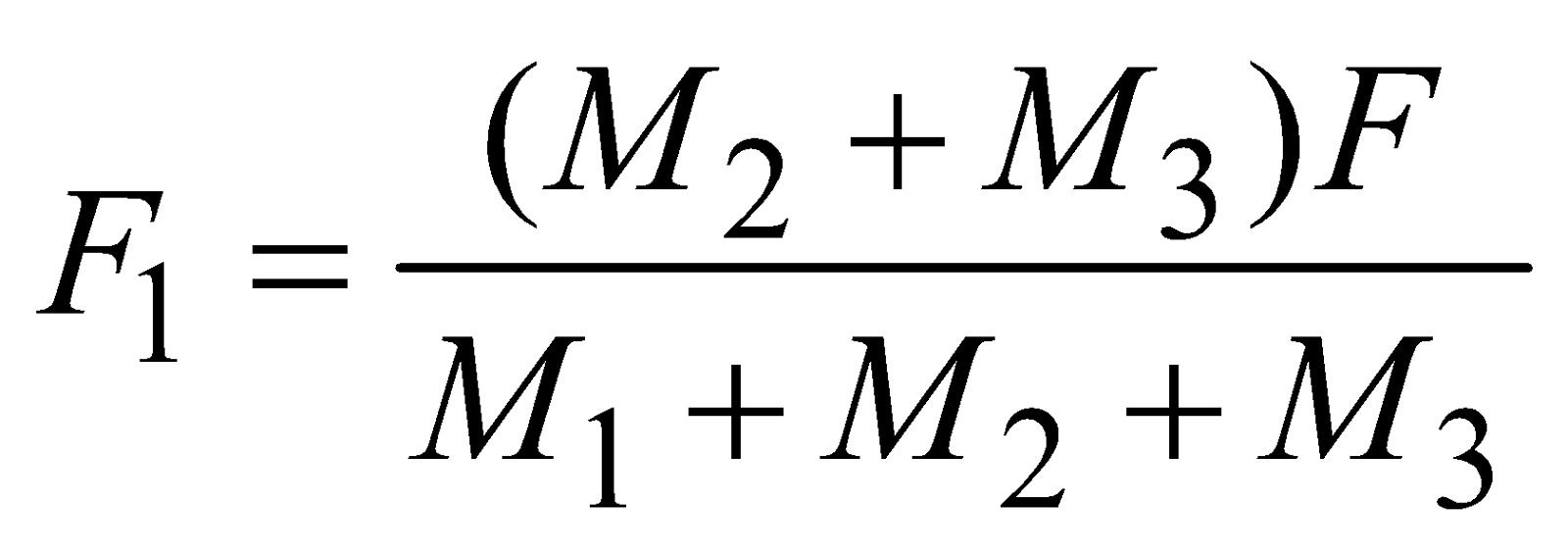
KEEP IN MEMORY
- When a man jumps with load on his head, the apparent weight of the load and the man is zero.
- If a person sitting in a train moving with uniform velocity throws a coin vertically up, then coin will fall back in his hand.
- If the train is uniformly accelerated, the coin will fall behind him.
- If the train is retarded uniformly, then the coin will fall in front of him.
LAW OF CONSERVATION OF LINEAR MOMENTUM
A system is said to be isolated, when no external force acts on it. For such isolated system, the linear momentum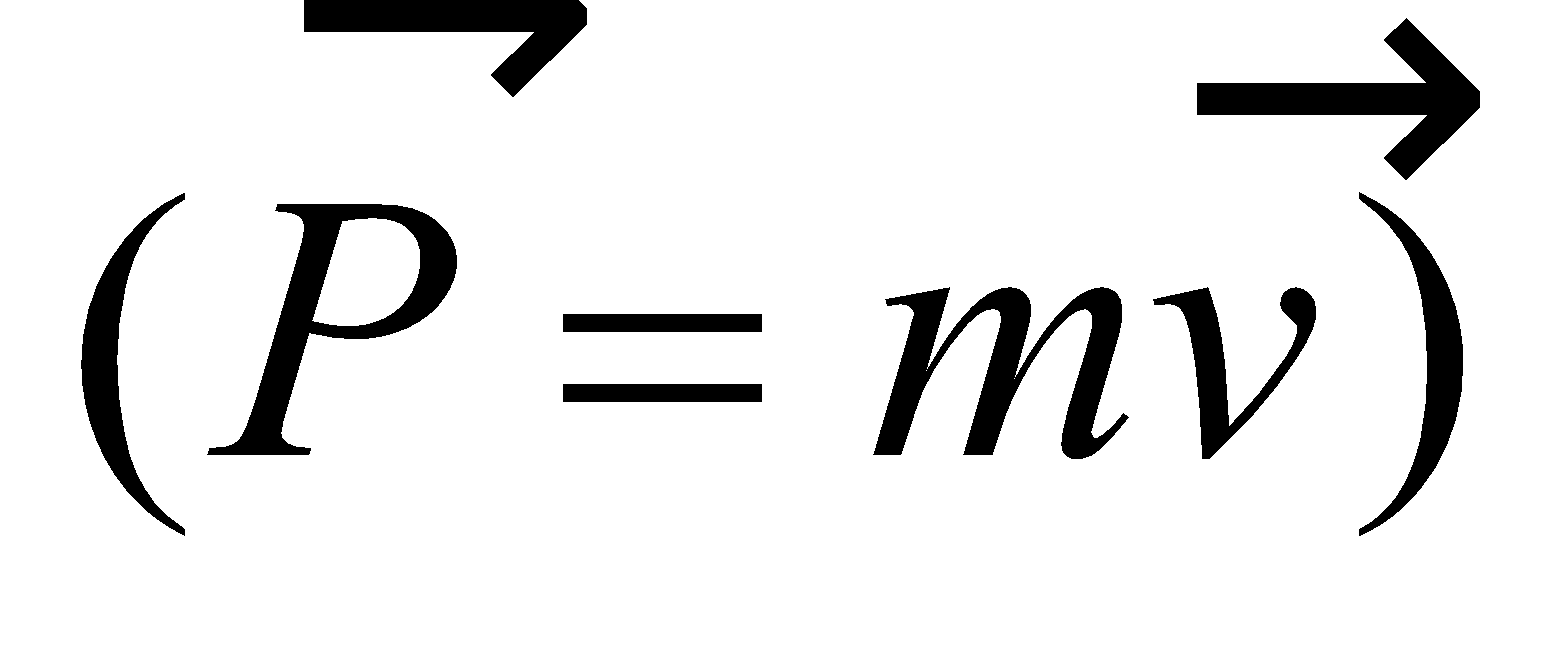 is constant i.e., conserved.
is constant i.e., conserved.
The linear momentum is defined as
where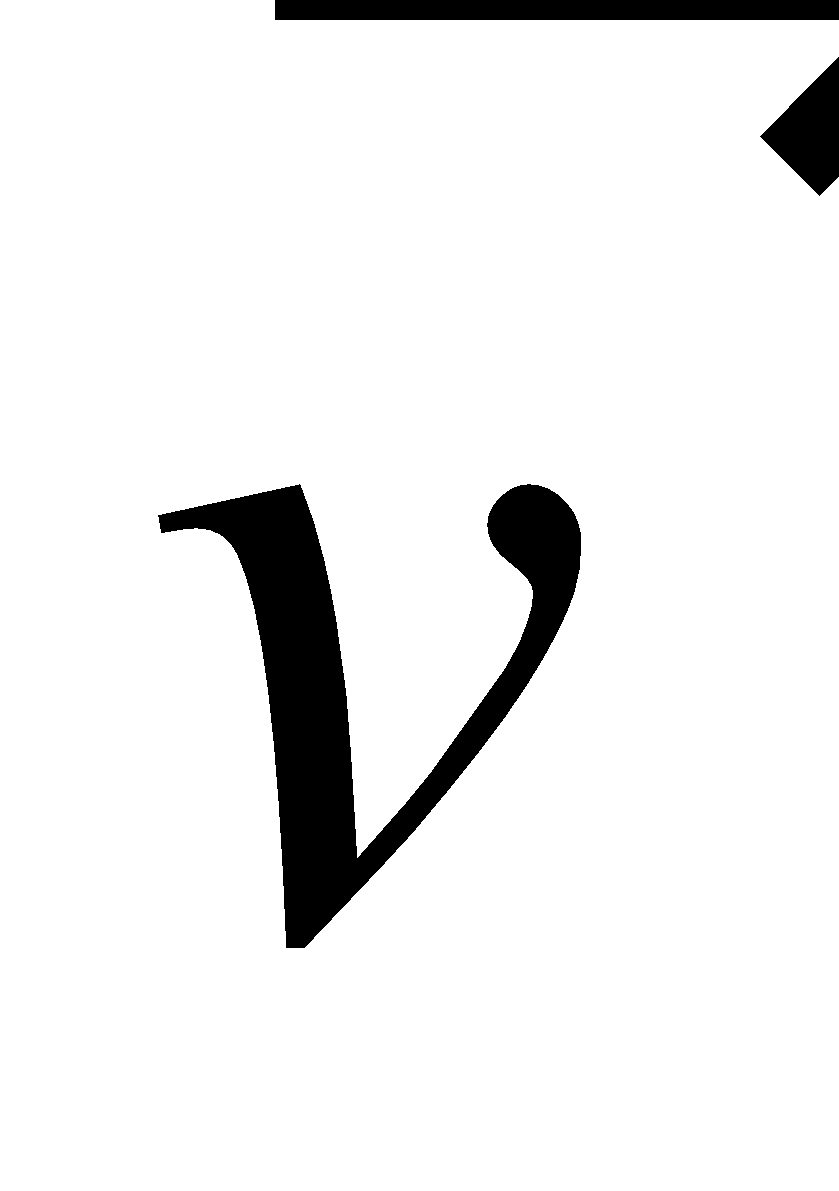 is the velocity of the body, whose mass is m. The direction of
is the velocity of the body, whose mass is m. The direction of  is same as the direction of the velocity of the body. It is a vector quantity. From Newton’s second law,
is same as the direction of the velocity of the body. It is a vector quantity. From Newton’s second law,
i.e., time rate of change in momentum of the body is equal to total external force applied on the body.
If 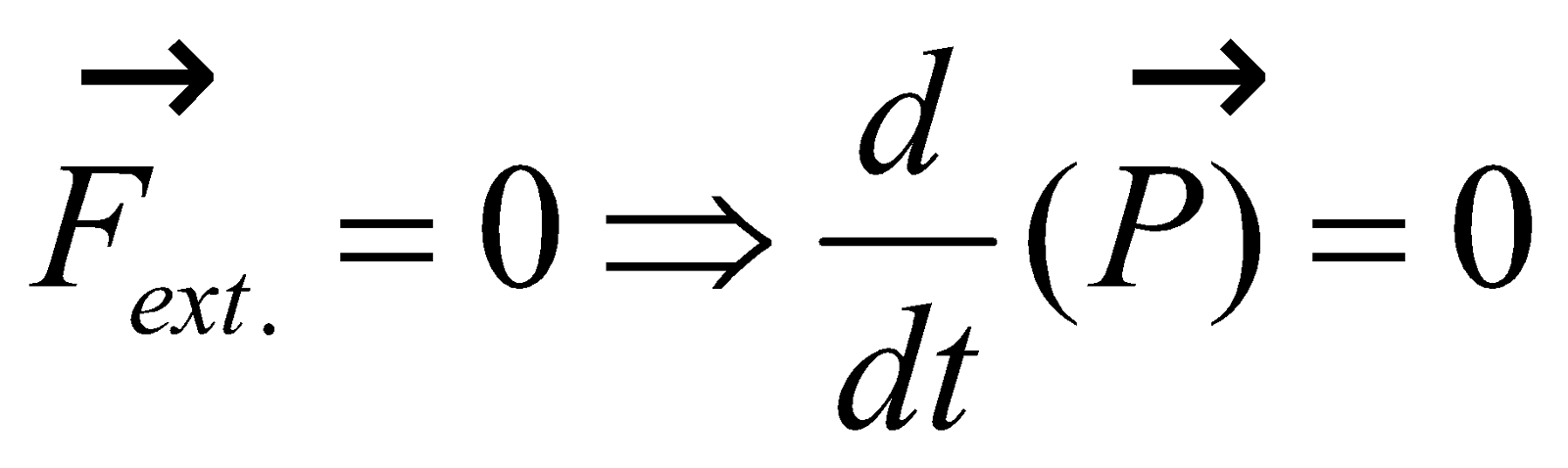 or
or  = constant …..(3)
= constant …..(3)
This is called law of conservation of momentum.
Now let us consider a rigid body consisting of a large number of particles moving with different velocities, then total linear momentum of the rigid body is equal to the summation of individual linear momentum of all particles
i.e., 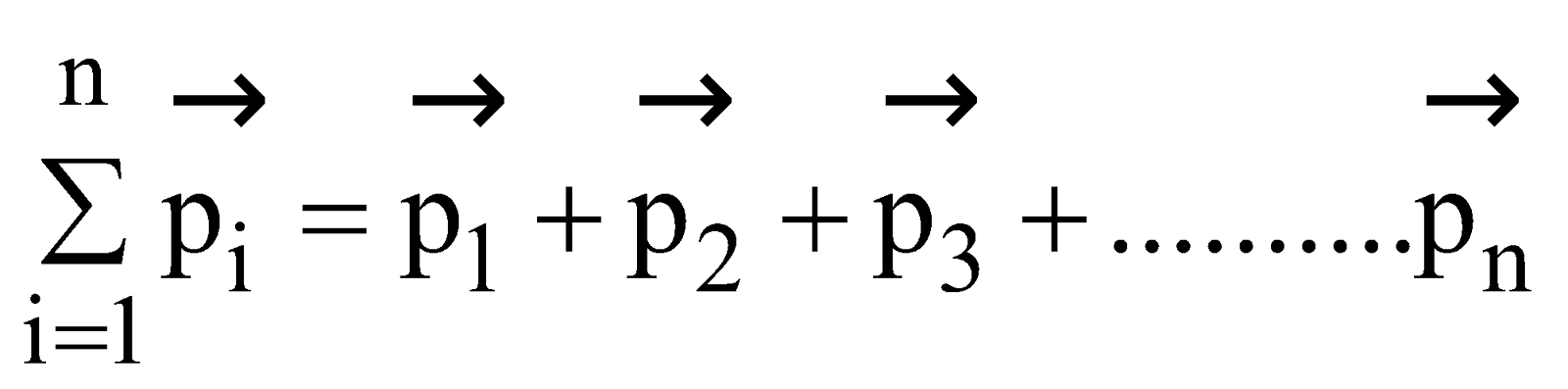
or 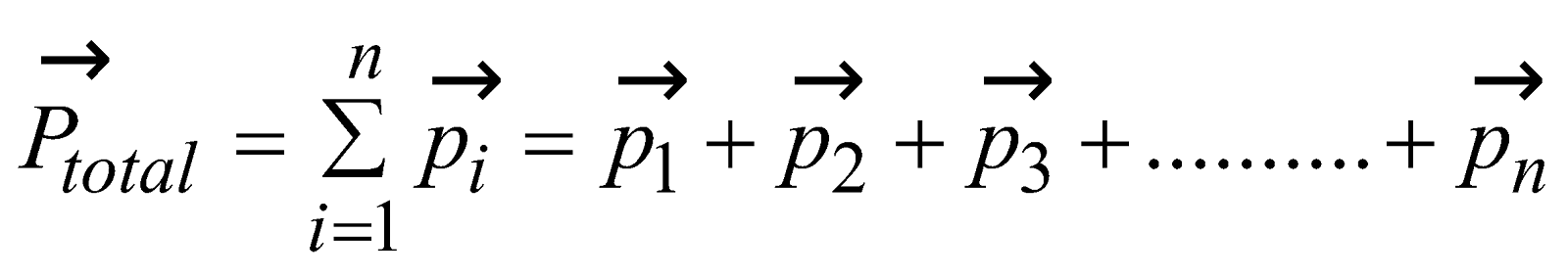
where  are individual linear momentum of first, second and nth particle respectively.
are individual linear momentum of first, second and nth particle respectively.
If this rigid body is isolated i.e., no external force is applied on it, then 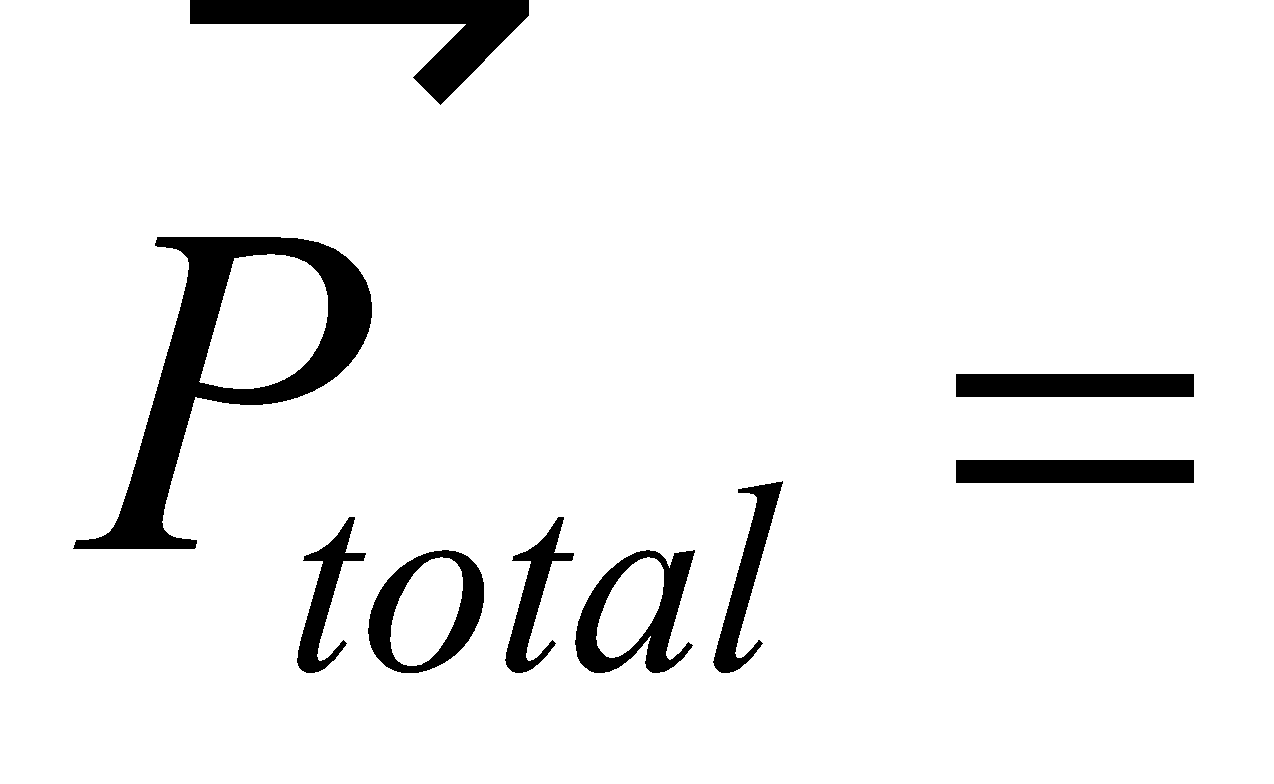 constant (from Newton’s second law).
constant (from Newton’s second law).
Further we know that internal forces (such as intermolecular forces etc.) also act inside the body, but these can only change individual linear momentum of the particles
(i.e., p1, p2………), but their total momentum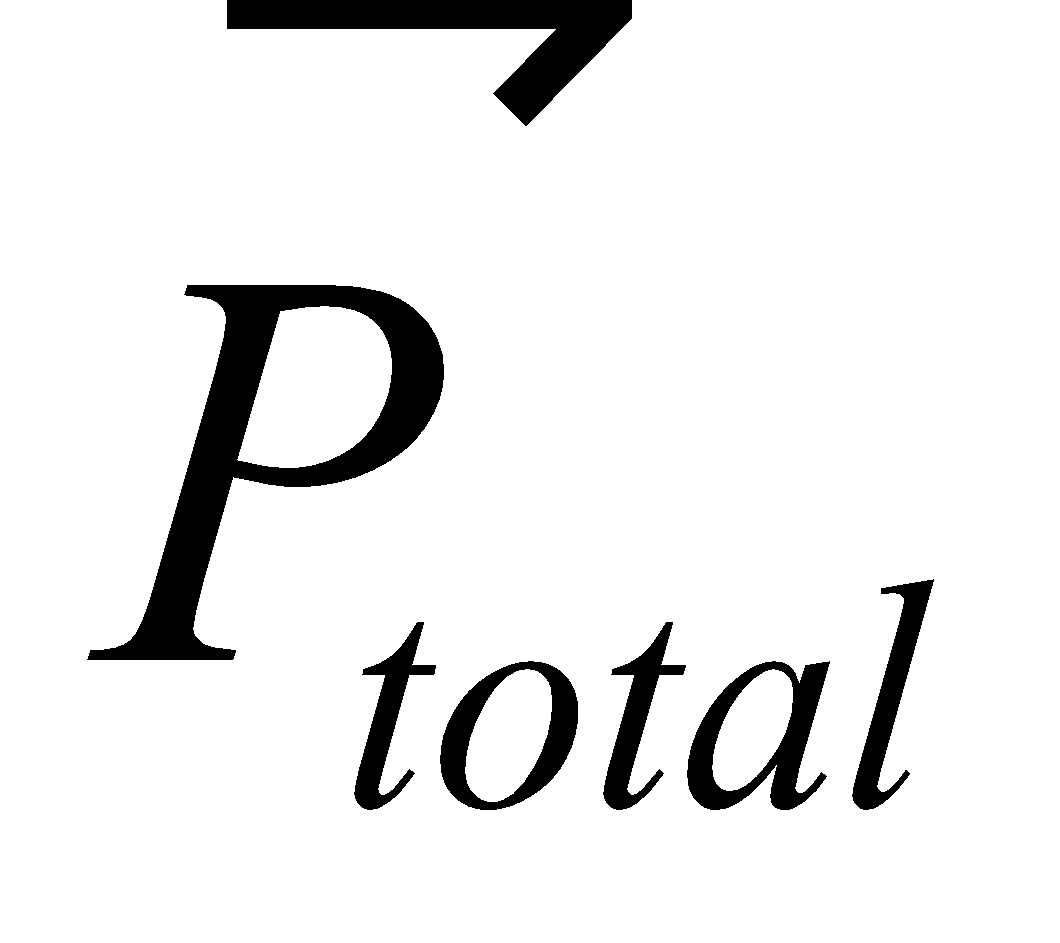 remains constant.
remains constant.
(i.e., p1, p2………), but their total momentum
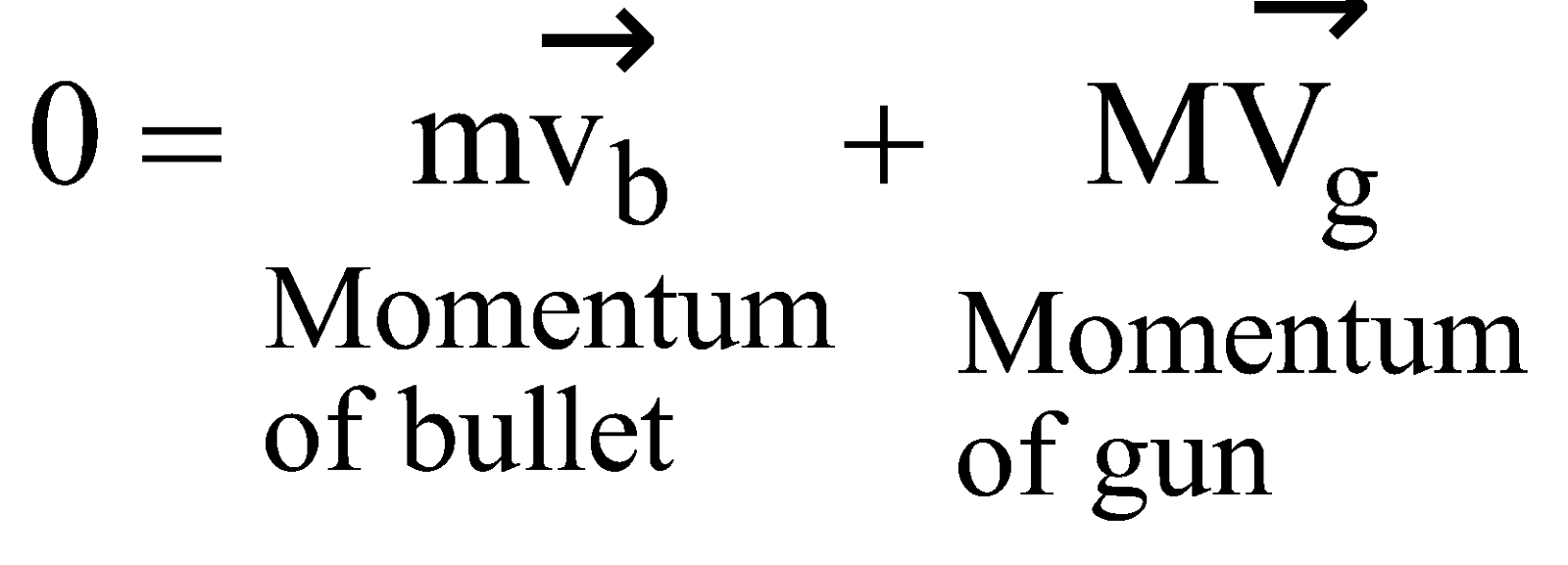
GUN FIRING A BULLET
If a gun of mass M fires a bullet of mass m with velocity v. Then from law of conservation of momentum, as initially bullet & gun are at rest position i.e., initial momentum is zero, so final momentum (gun + bullet) must also be zero.
Since on firing, the bullet moves with velocity 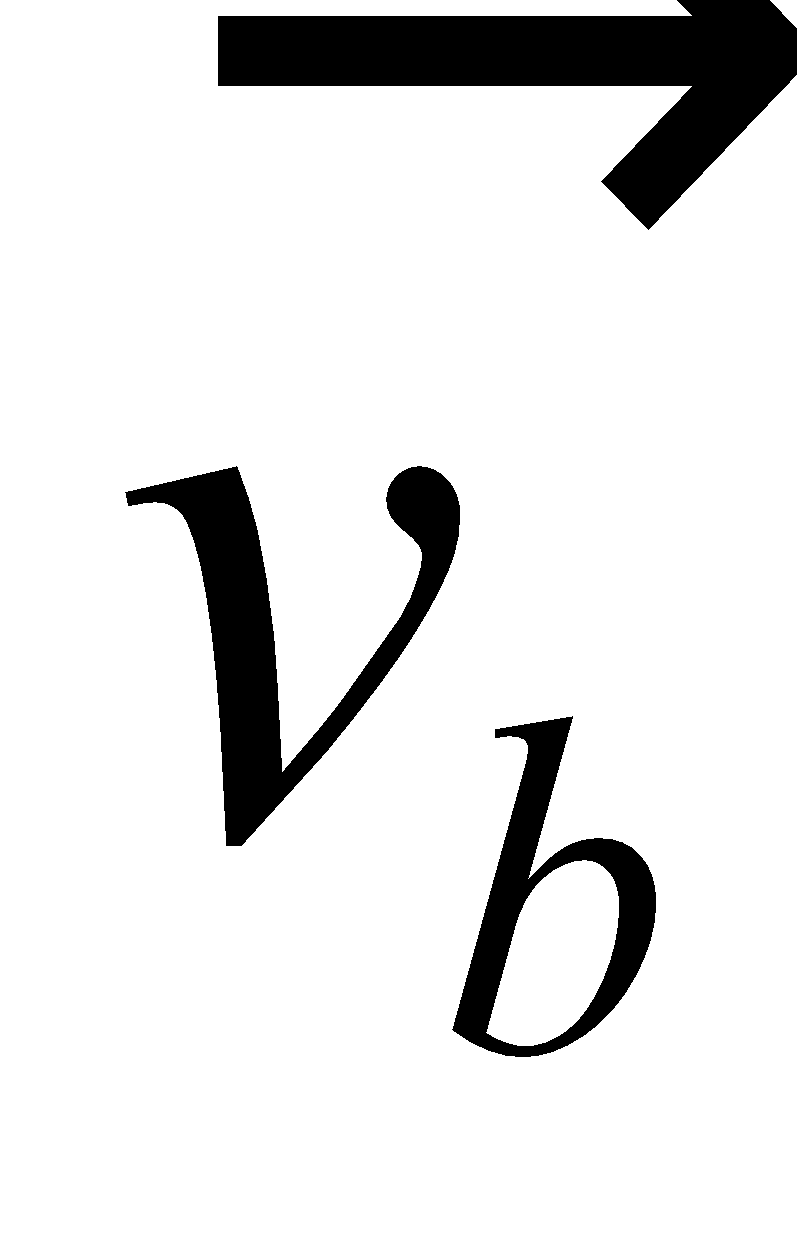 in forward direction, then from Newton’s third law, the gun moves in backward direction
in forward direction, then from Newton’s third law, the gun moves in backward direction  . So,
. So,
Initial momentum = final momentum
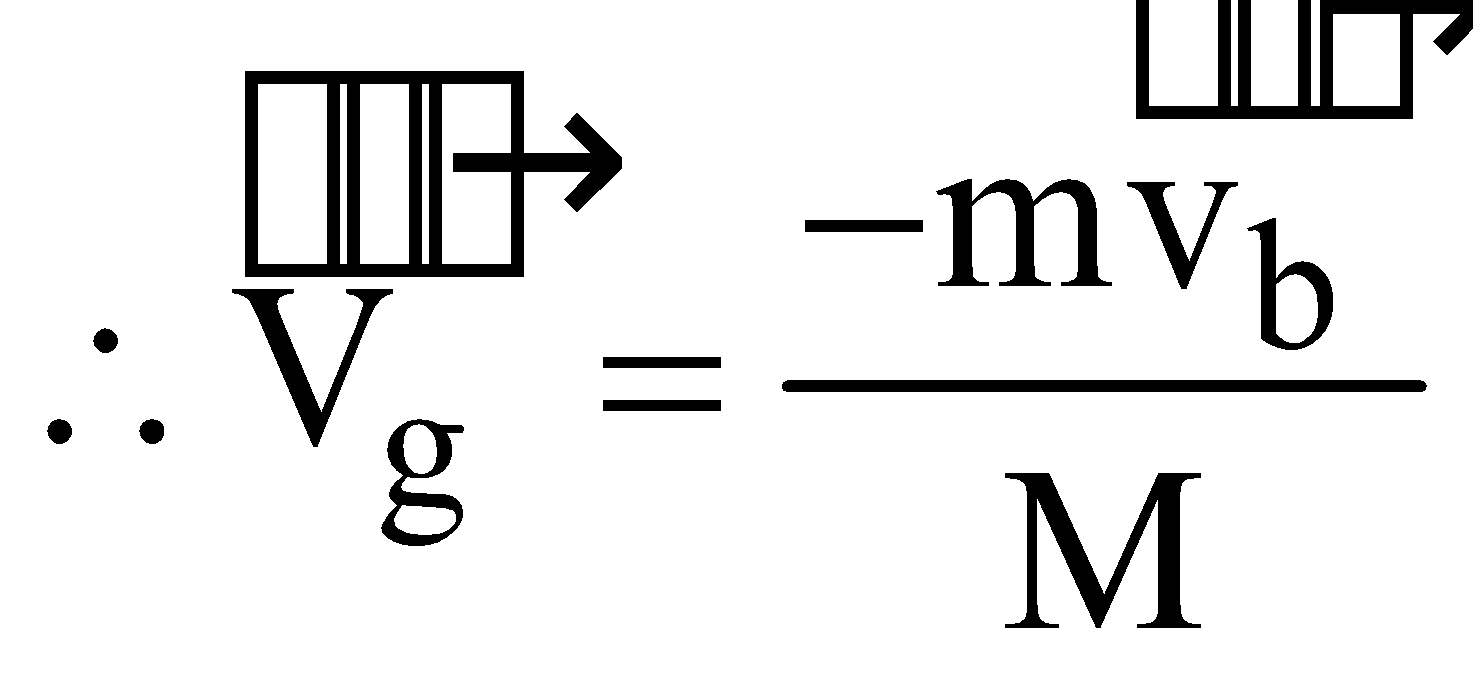
(–ve sign shows that the vel. of gun will have the opposite direction to that of bullet)
IMPULSE
According to Newton’s second law the rate of change of momentum of a particle is equal to the total external force applied on it (particle) i.e.,
or 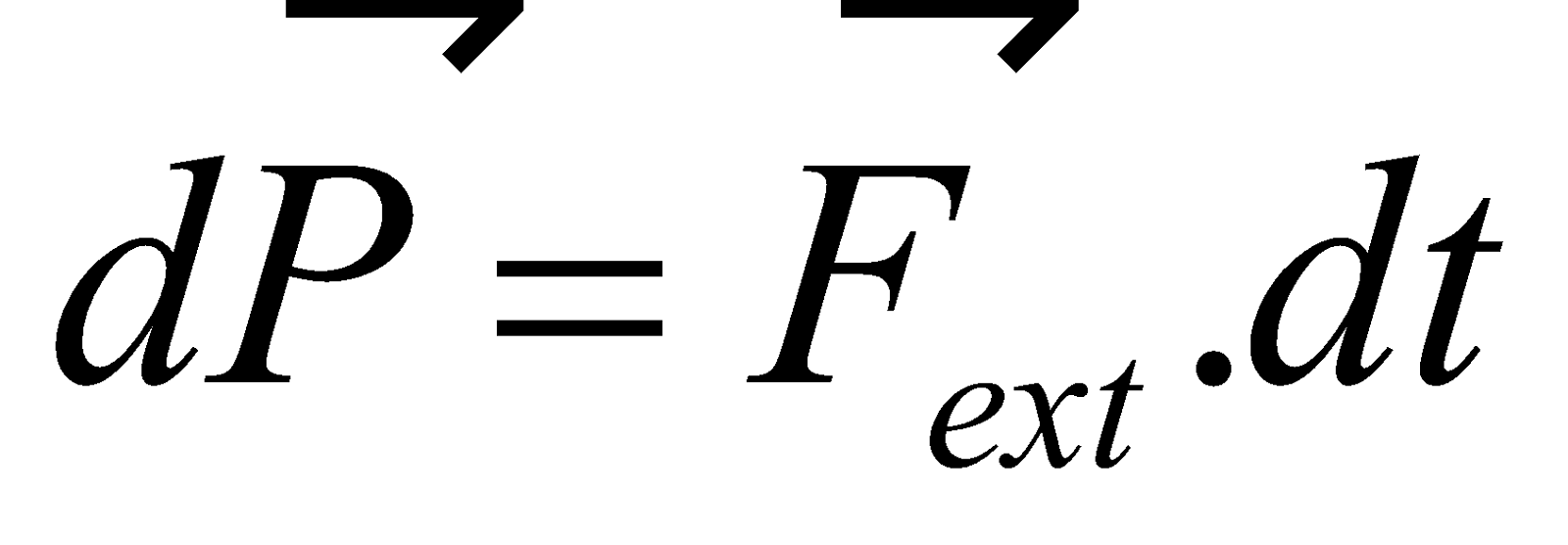 or
or 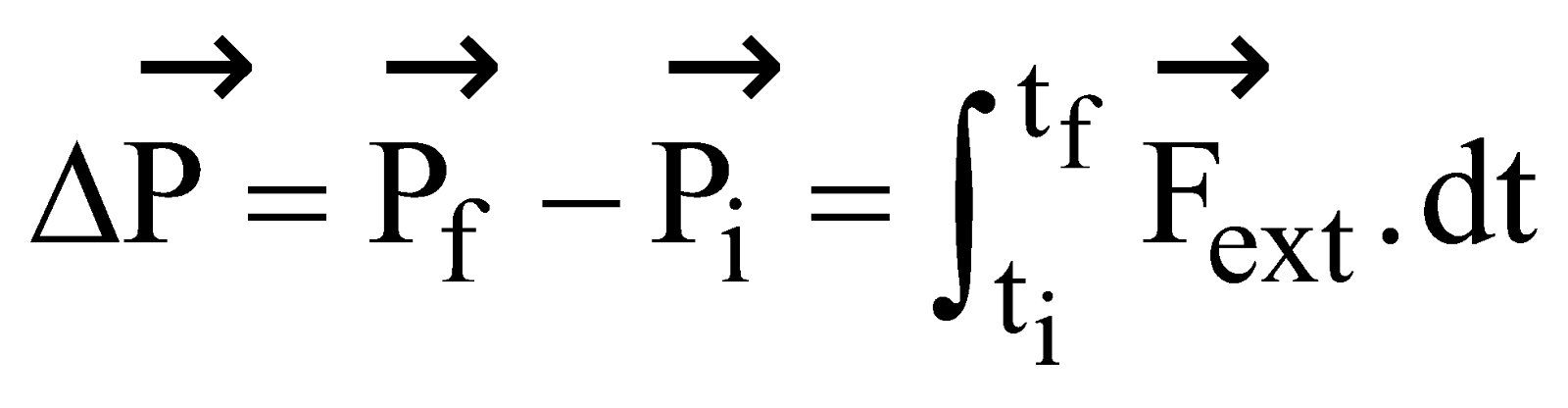 …(ii)
…(ii)
Where 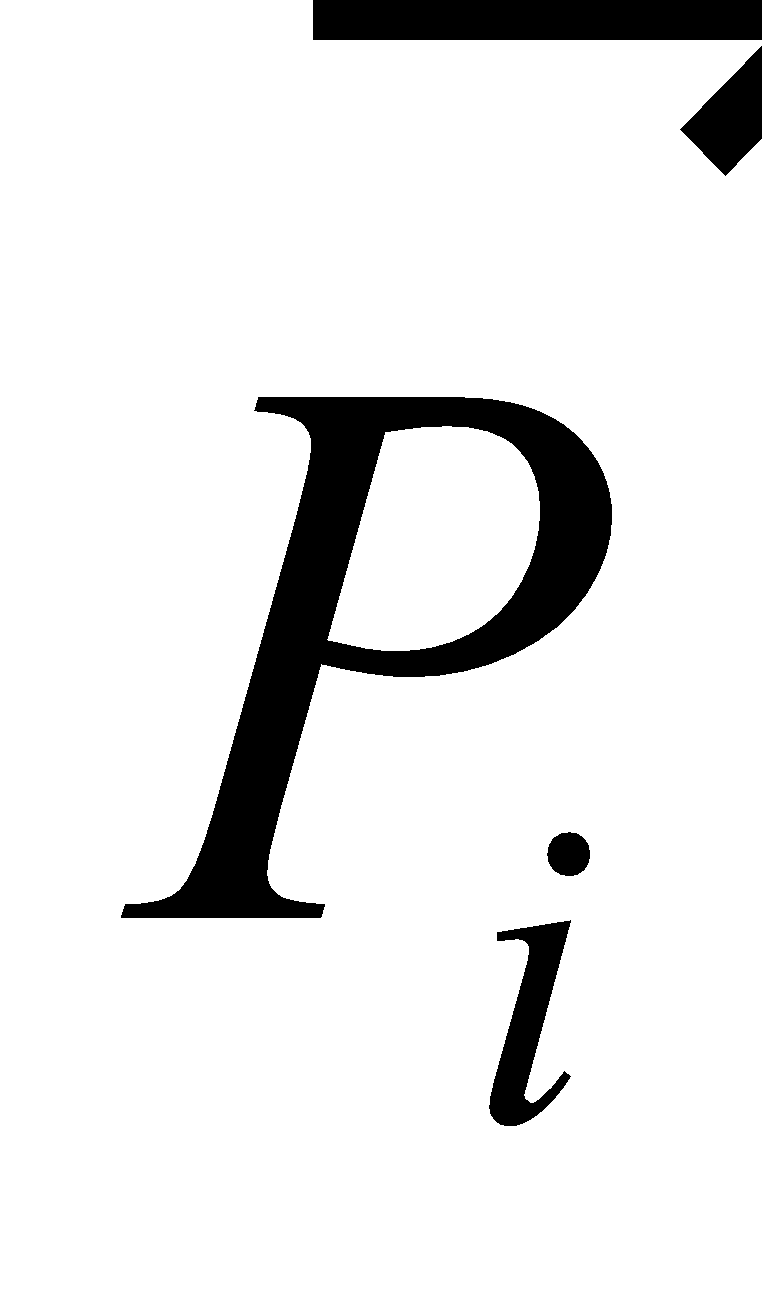 is momentum of the particle at initial time ti and when we apply some external force
is momentum of the particle at initial time ti and when we apply some external force 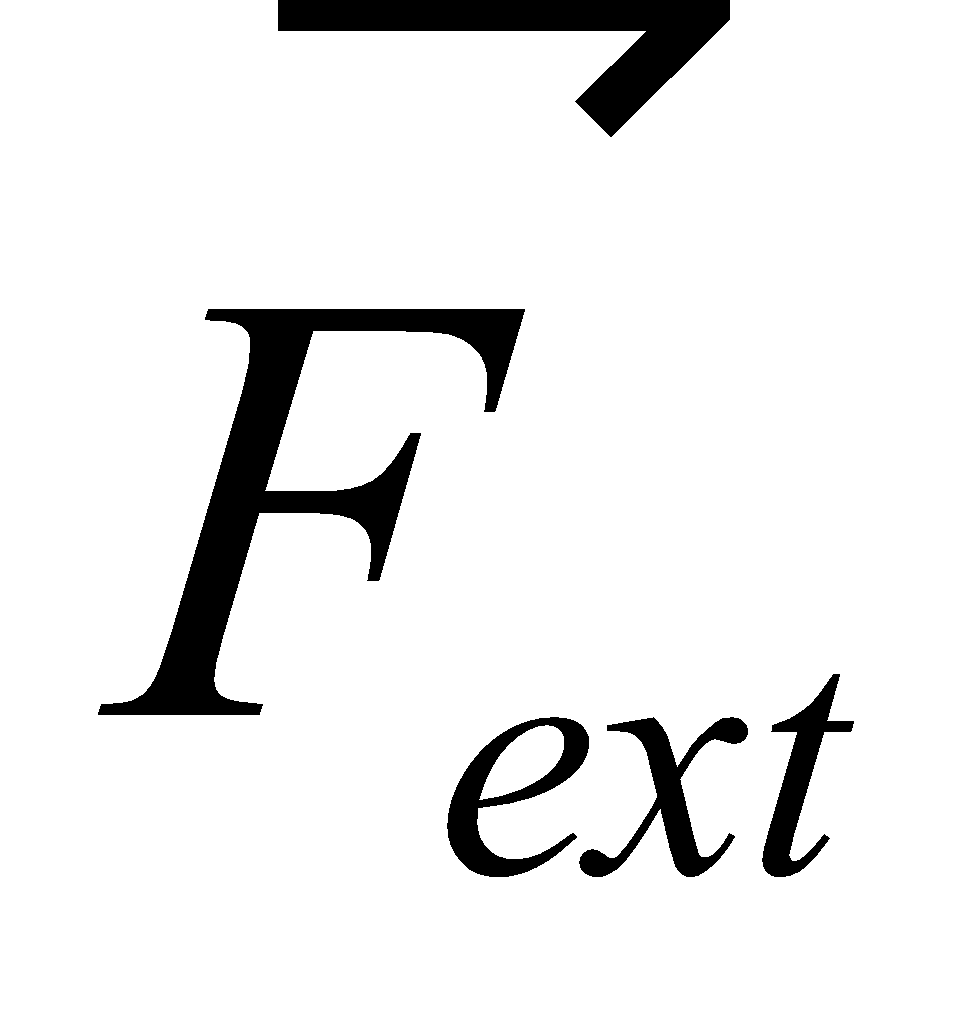 its final momentum is
its final momentum is 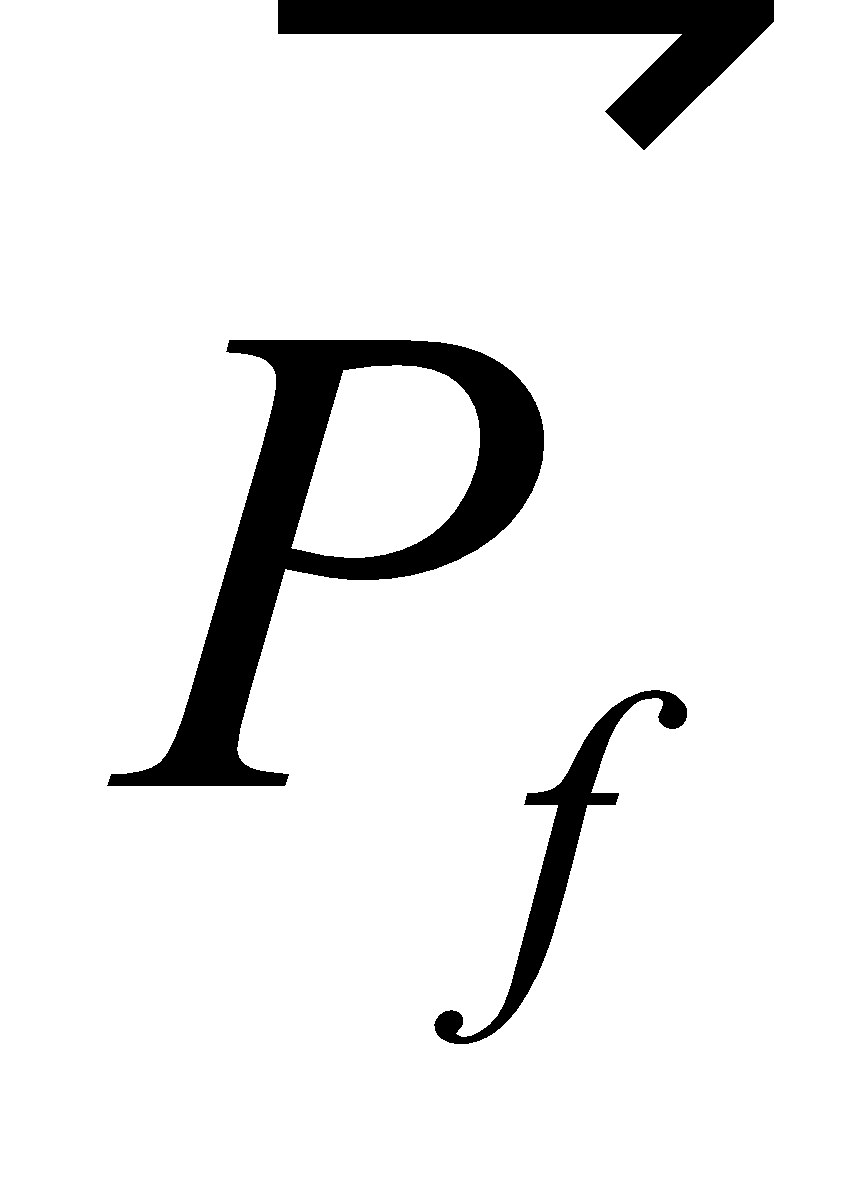 at time tf . The quantity
at time tf . The quantity 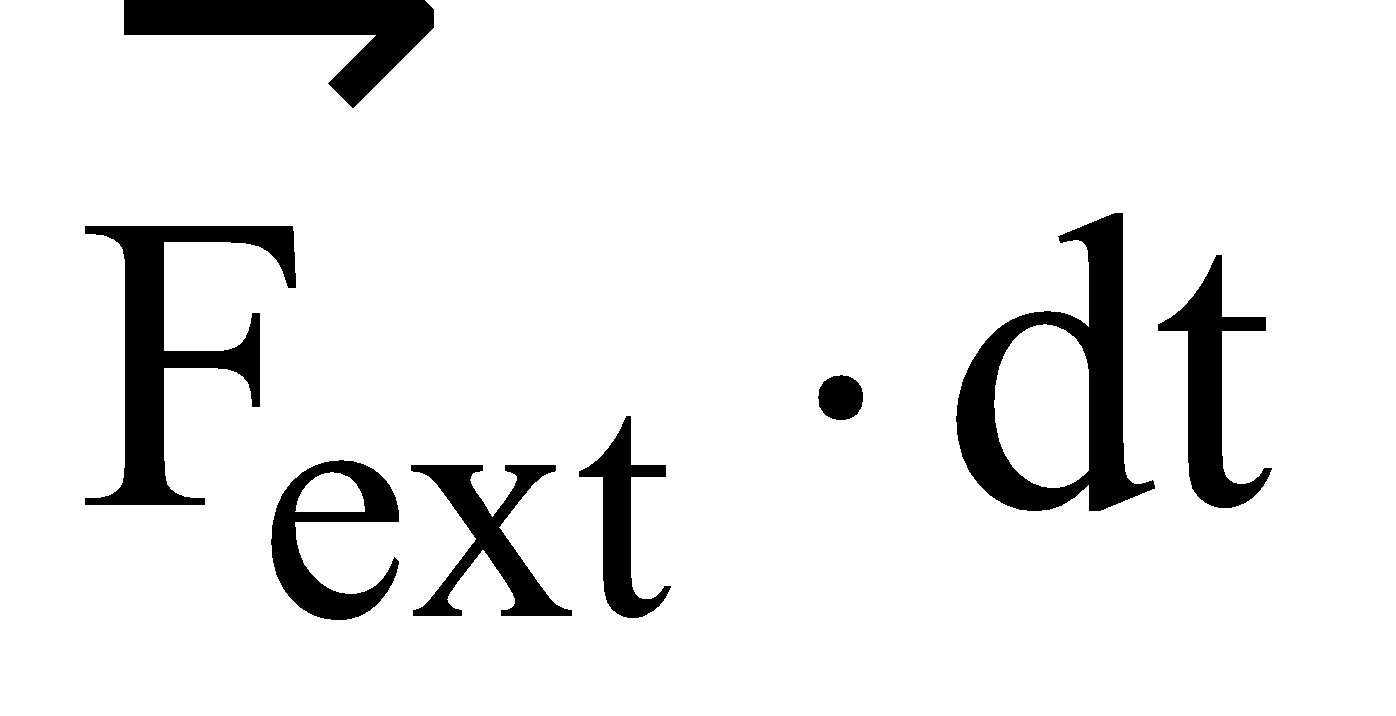 on R.H.S in equation (ii) is called the impulse.
on R.H.S in equation (ii) is called the impulse.
We can write equation (ii) as
So, the impulse of the force 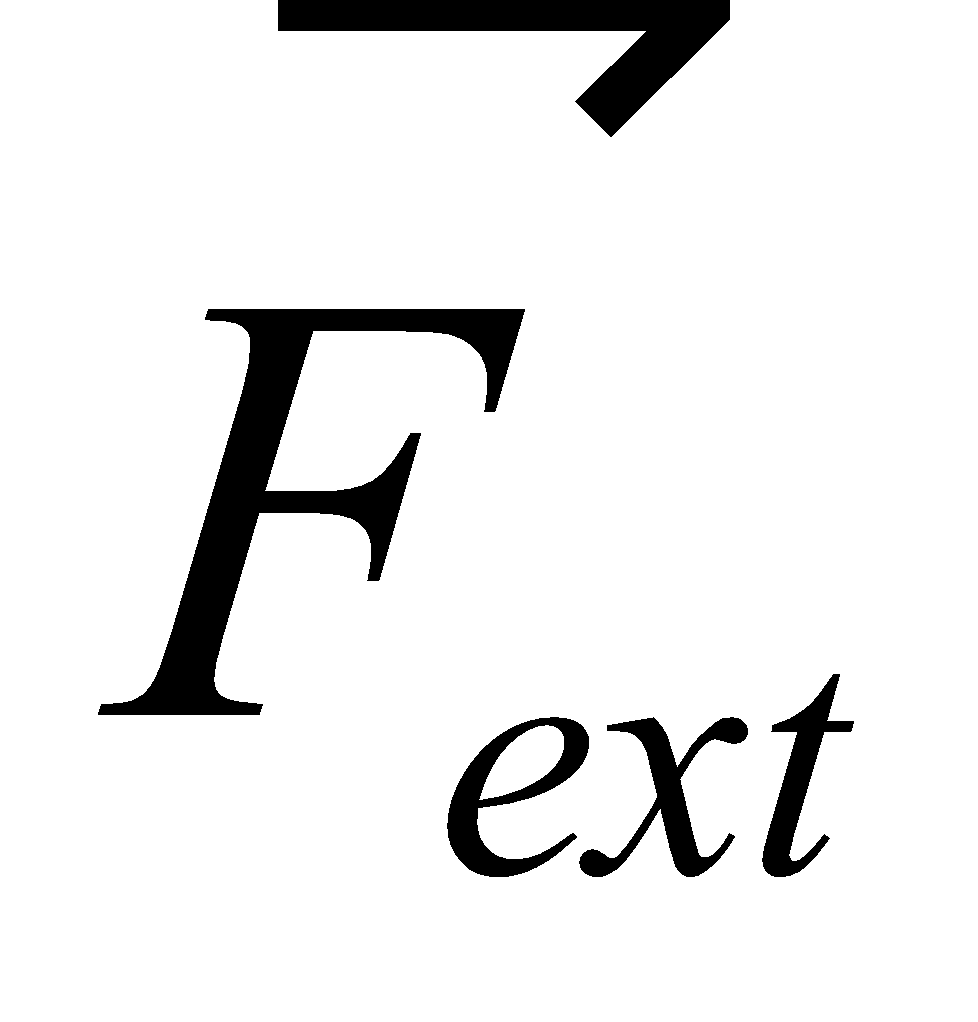 is equal to the change in momentum of the particle. It is known as impulse momentum theorem.
is equal to the change in momentum of the particle. It is known as impulse momentum theorem.
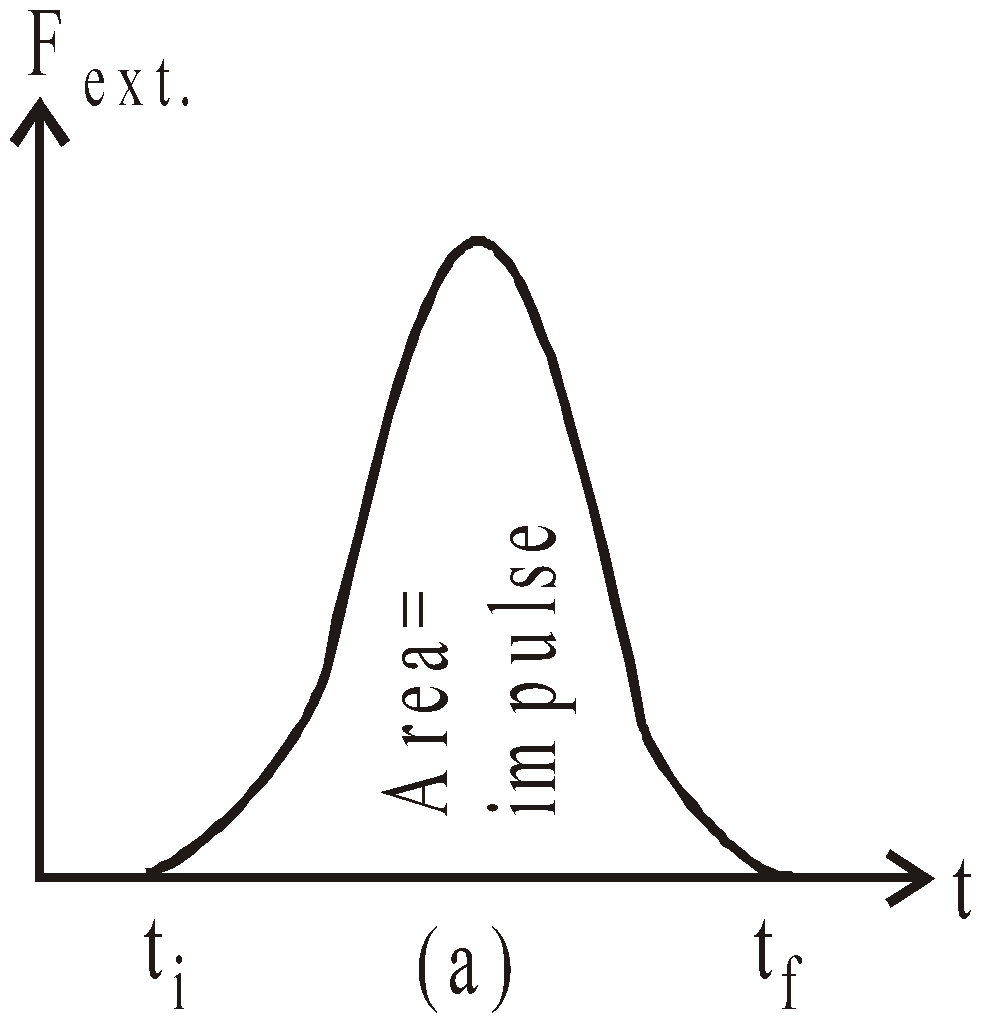
Force vary with time and impulse is area under force versus time curve
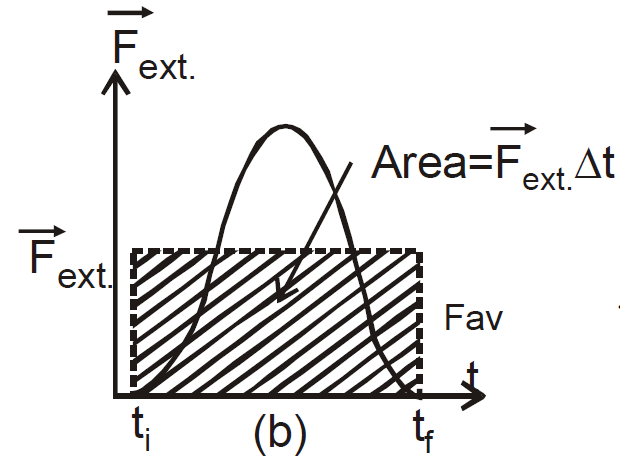
Force constant with time i.e., 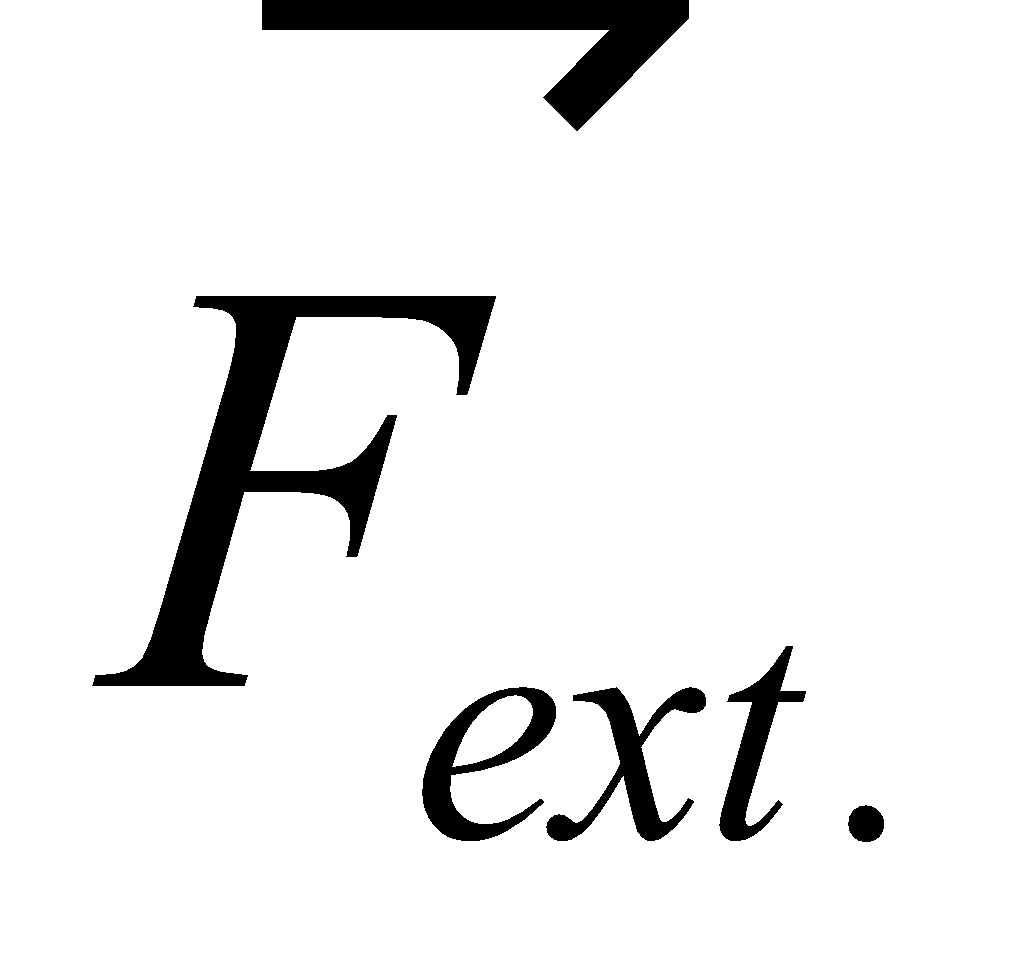 constant with time (shown by horizontal line) and it would give same impulse to particle in time Δt = tf–ti as time varying force described.
constant with time (shown by horizontal line) and it would give same impulse to particle in time Δt = tf–ti as time varying force described.
It is a vector quantity having a magnitude equal to the area under the force-time curve as shown in fig. (a). In this figure, it is assumed that force varies with time and is non-zero in time interval Δt = tf–ti. Fig.(b) shows the time averaged force i.e., it is constant in time interval Δt, then equation (iii) can be written as
The direction of impulsive vector I is same as the direction of change in momentum. Impulse I has same dimensions as that of momentum i.e, [MLT–1]
ROCKET PROPULSION (A CASE OF SYSTEM OF VARIABLE MASS)
It is based on principle of conservation of linear momentum.
In rocket, the fuel burns and produces gases at high temperature. These gases are ejected out of the rocket from nozzle at the backside of rocket and the ejecting gas exerts a forward force on the rocket which accelerates it.
Let the gas ejects at a rate 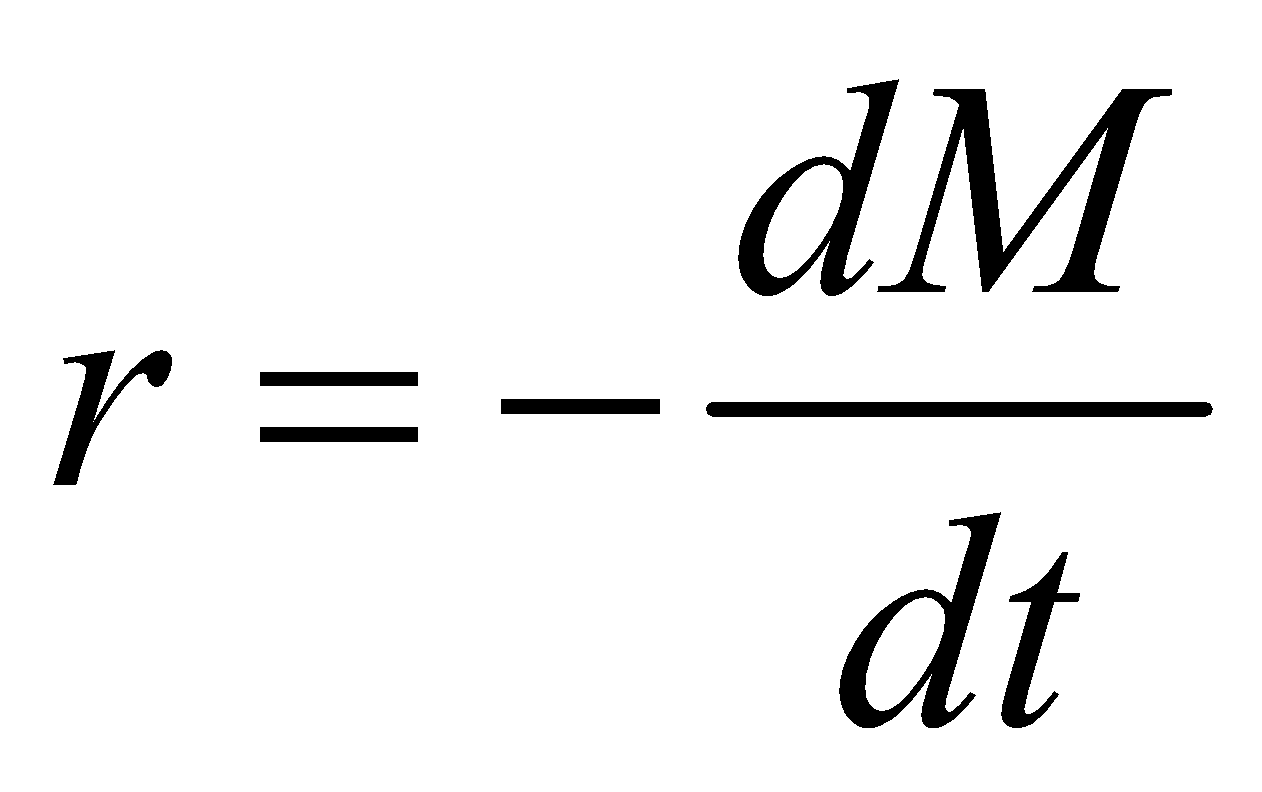
and at constant velocity u w.r.t. rocket then from the conservation of linear momentum 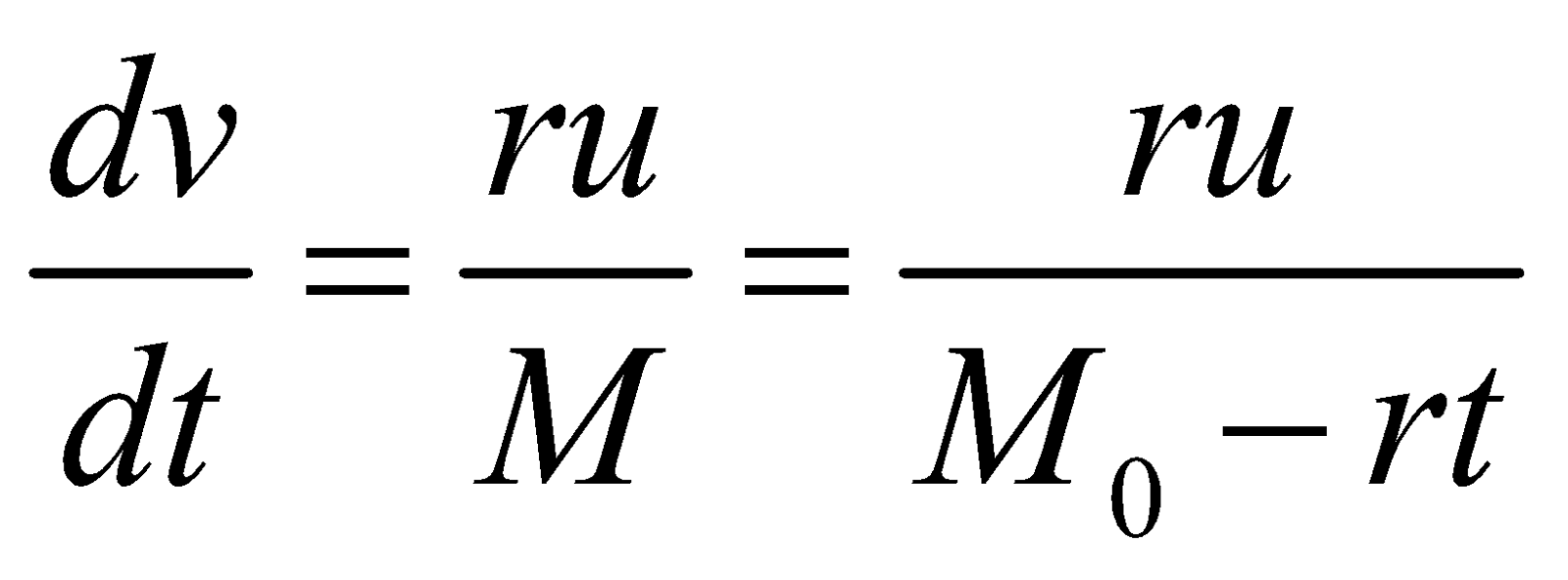
where M = M0 – rt and M0 is mass of rocket with fuel and solving this equation,
we get 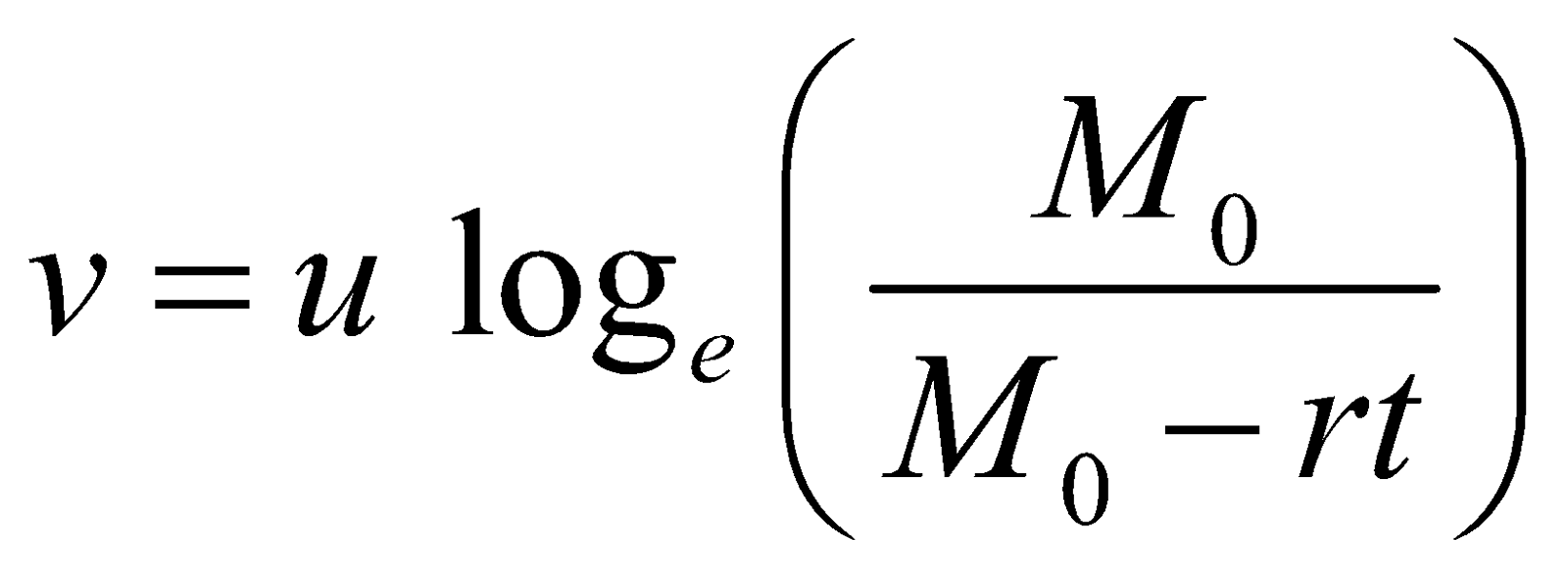
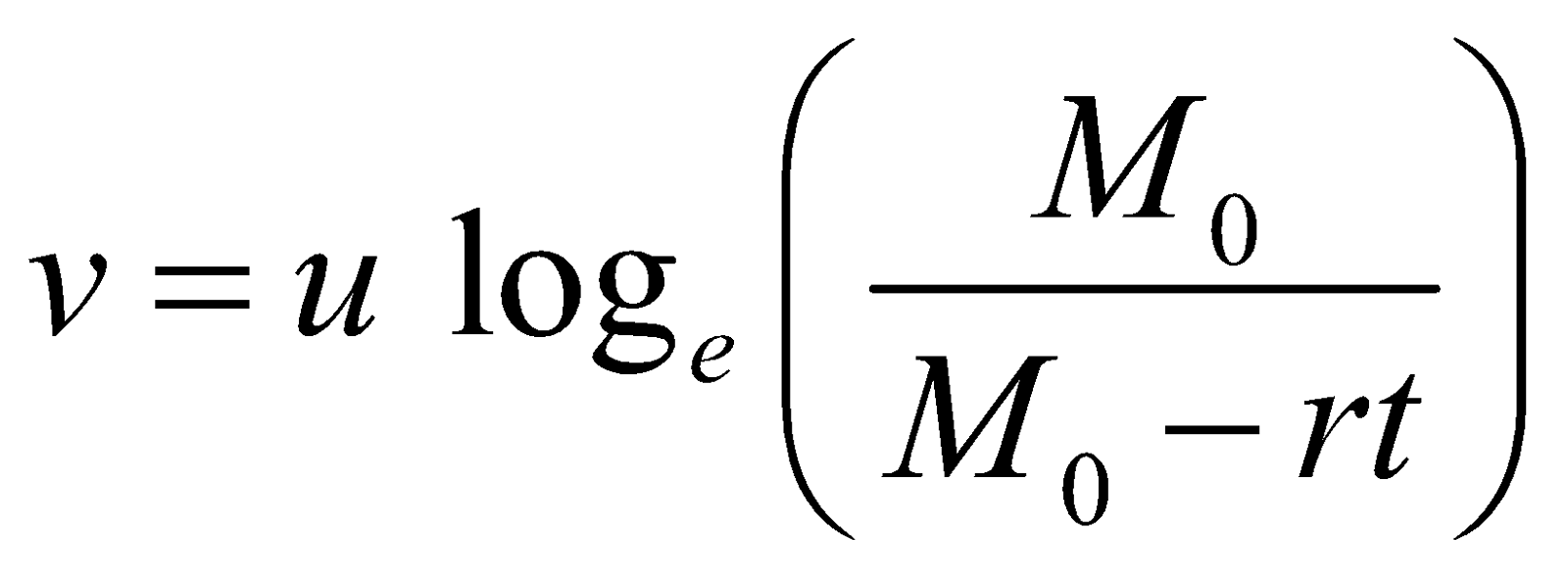
where v = velocity of rocket w.r.t. ground.
FRICTION
When a body is in motion on a rough surface, or when an object moves through water (i.e., viscous medium), then velocity of the body decreases constantly even if no external force is applied on the body. This is due to friction.
So “an opposing force which comes into existence, when two surfaces are in contact with each other and try to move relative to one another, is called friction”.
Frictional force acts along the common surface between the two bodies in such a direction so as to oppose the relative movement of the two bodies.
The force of static friction fs between book and rough surface is opposite to the applied external force Fext. The force of static friction fs =
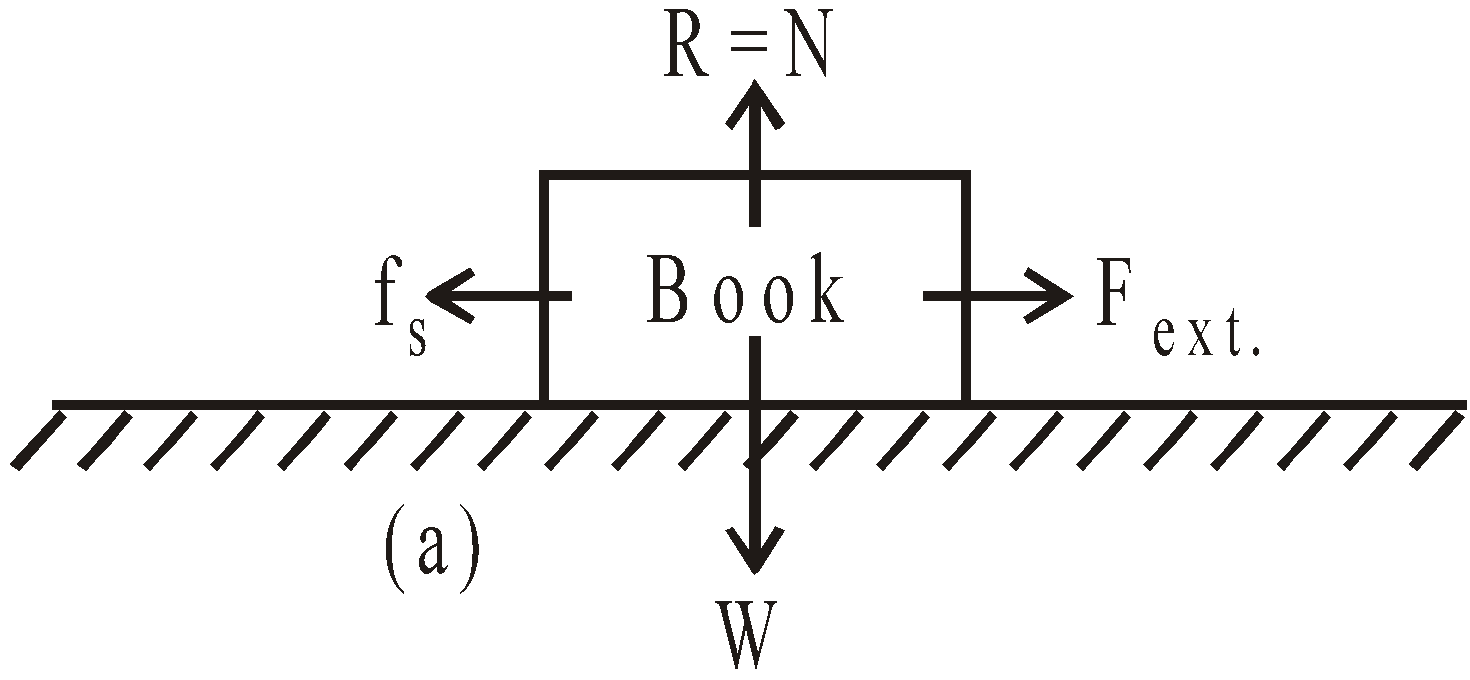
When  exceeds the certain maximum value of static friction, the book starts accelerating and during motion Kinetic frictional force is present.
exceeds the certain maximum value of static friction, the book starts accelerating and during motion Kinetic frictional force is present.
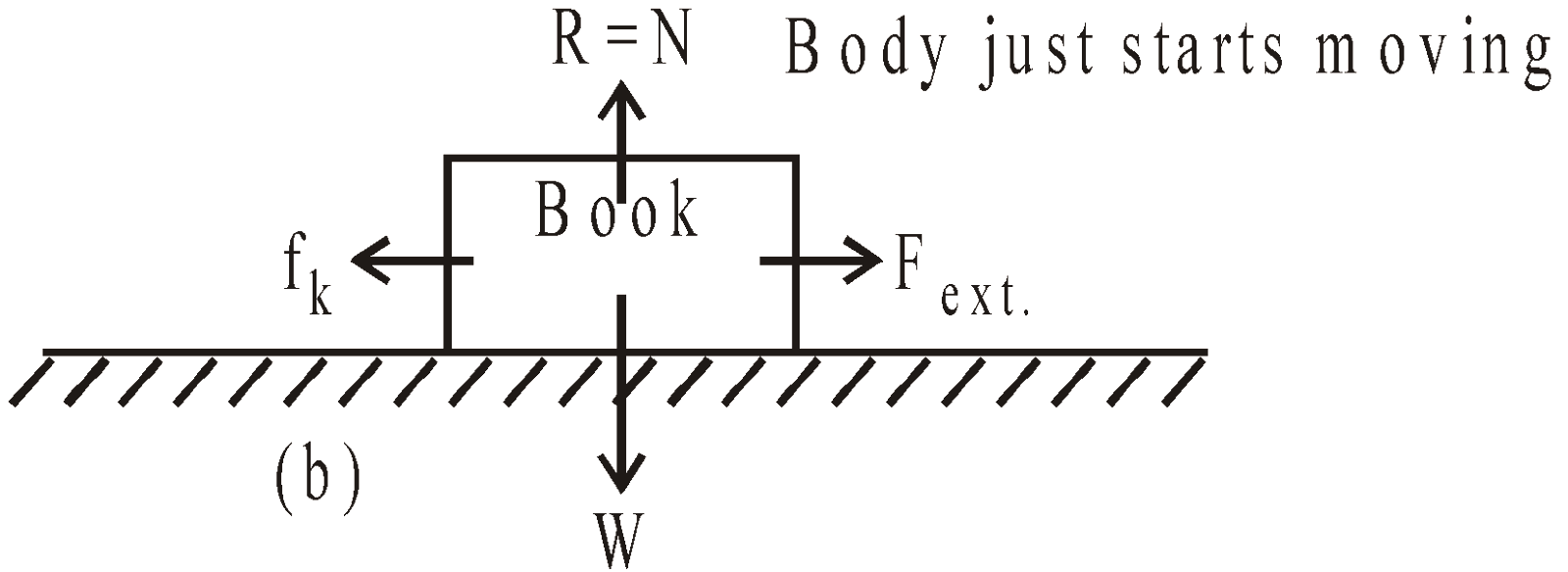
A graph  versus | f | shown in figure. It is clear that fs, ,max > fk
versus | f | shown in figure. It is clear that fs, ,max > fk
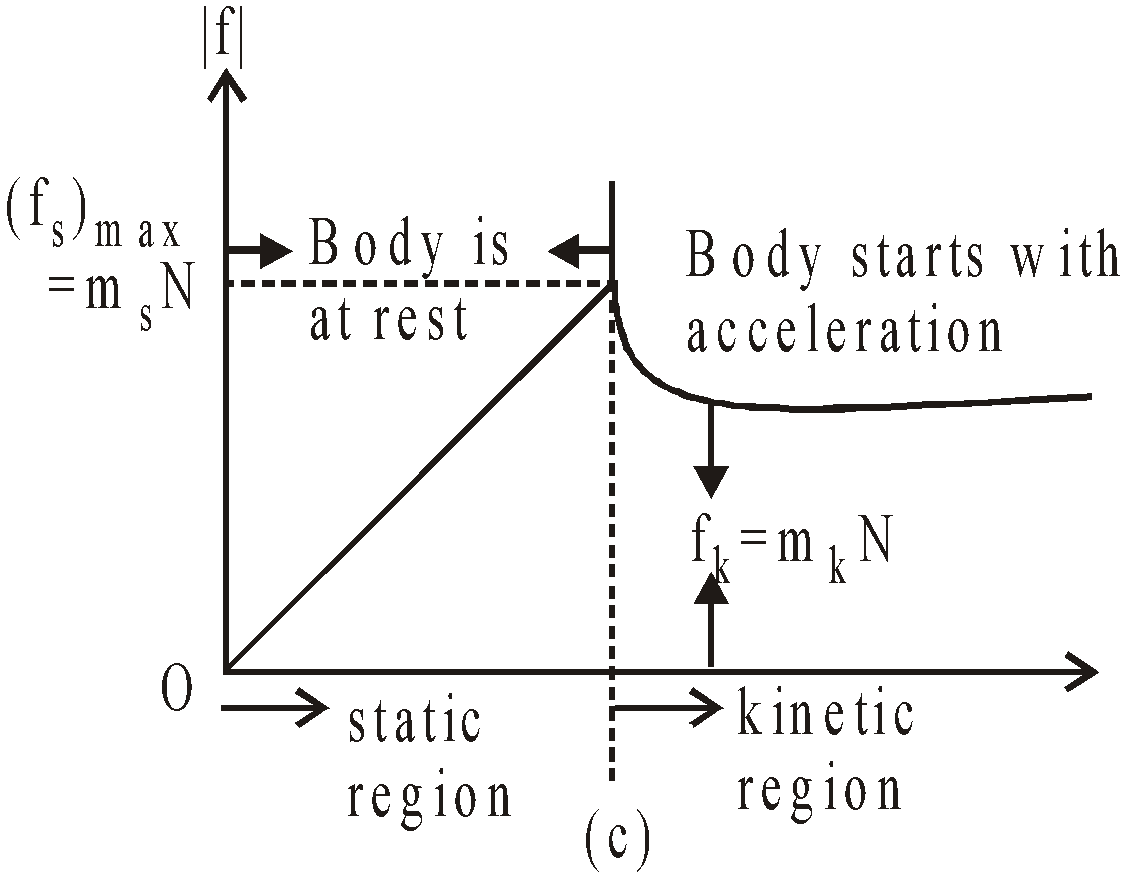
Fig.(a) shows a book on a horizontal rough surface. Now if we apply external force  , on the book, then the book will remain stationary if
, on the book, then the book will remain stationary if 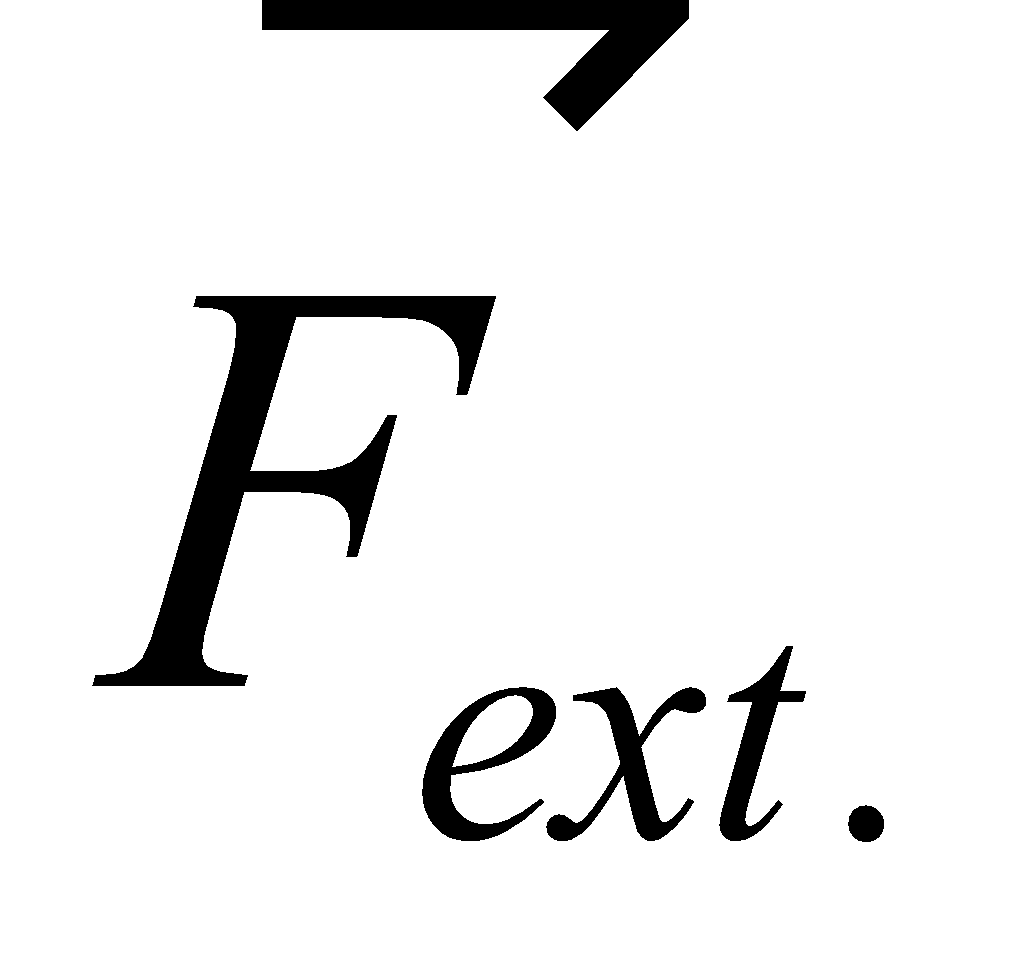 is not too large. If we increase
is not too large. If we increase 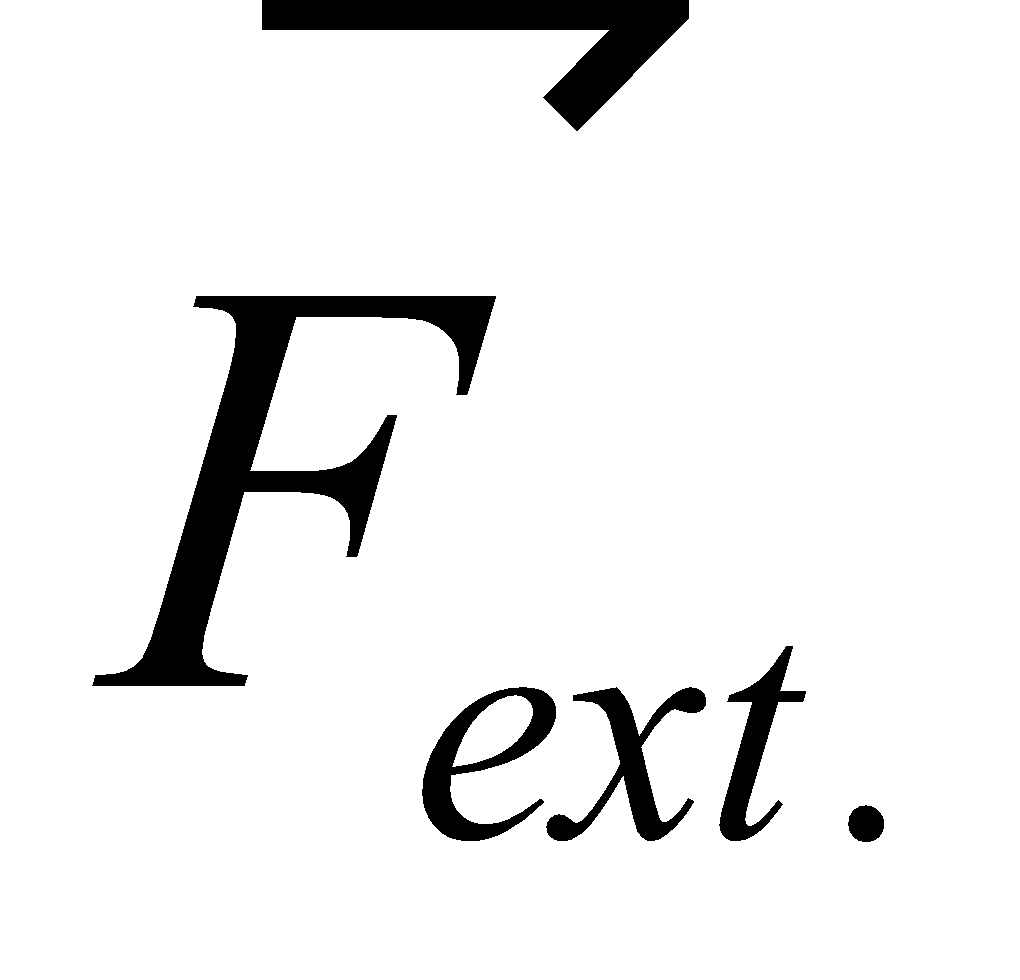 then frictional force f also increase up to
then frictional force f also increase up to 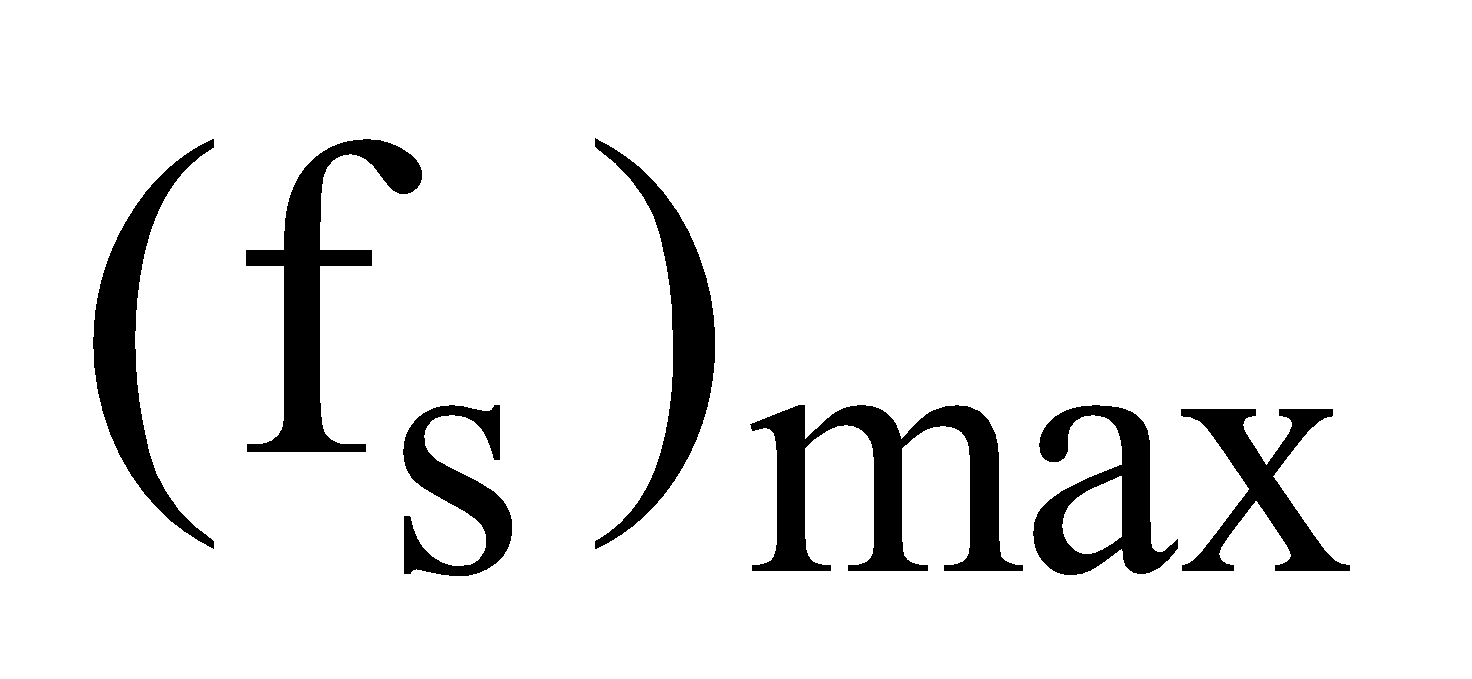 (called maximum force of static friction or limiting friction) and
(called maximum force of static friction or limiting friction) and  = μsN. At any instant when
= μsN. At any instant when 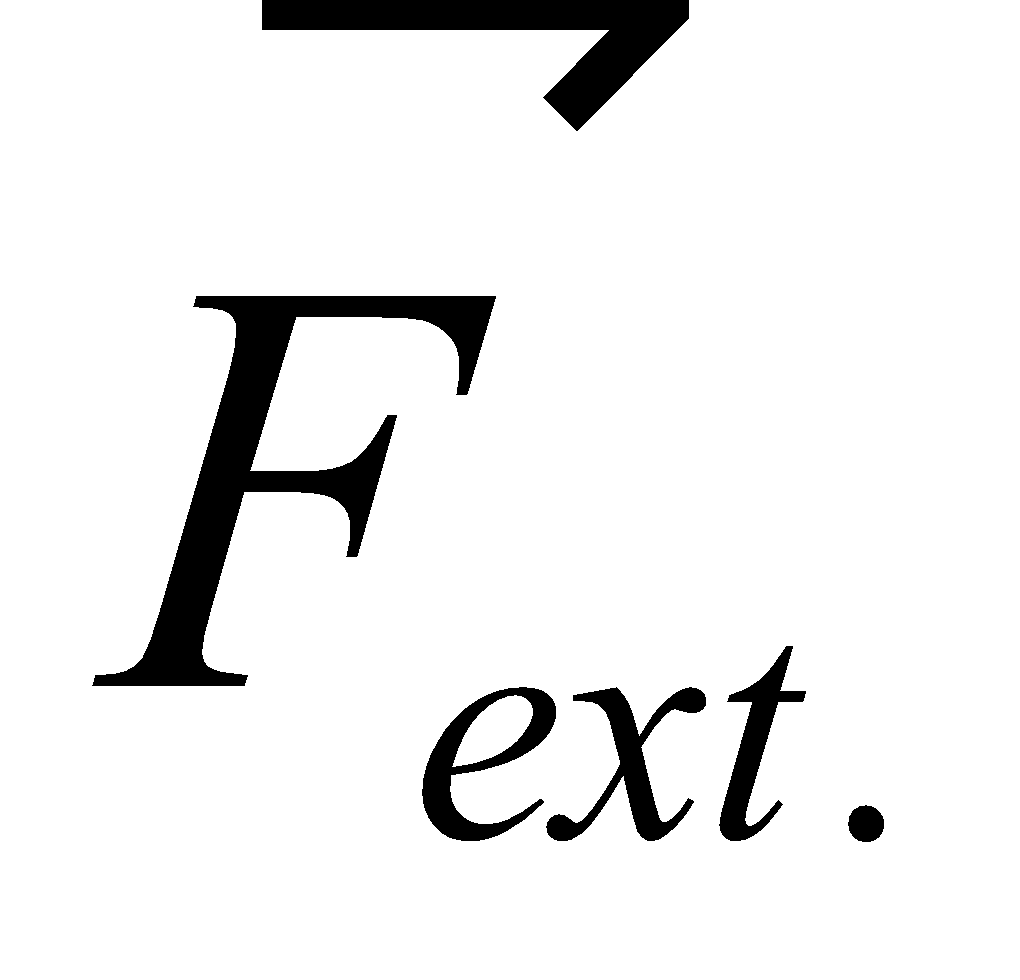 is slightly greater than
is slightly greater than 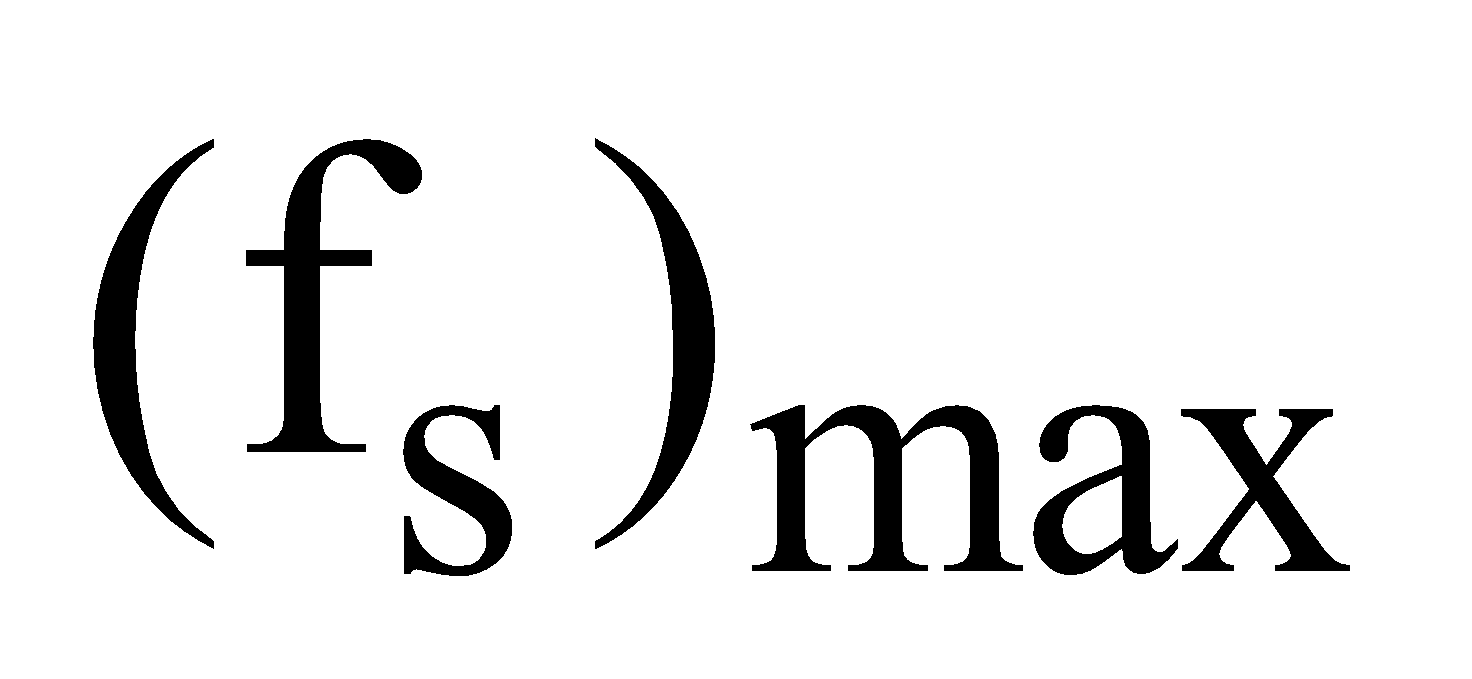 then the book moves and accelerates to the right.
then the book moves and accelerates to the right.
Fig.(b) when the book is in motion, the retarding frictional force become less than 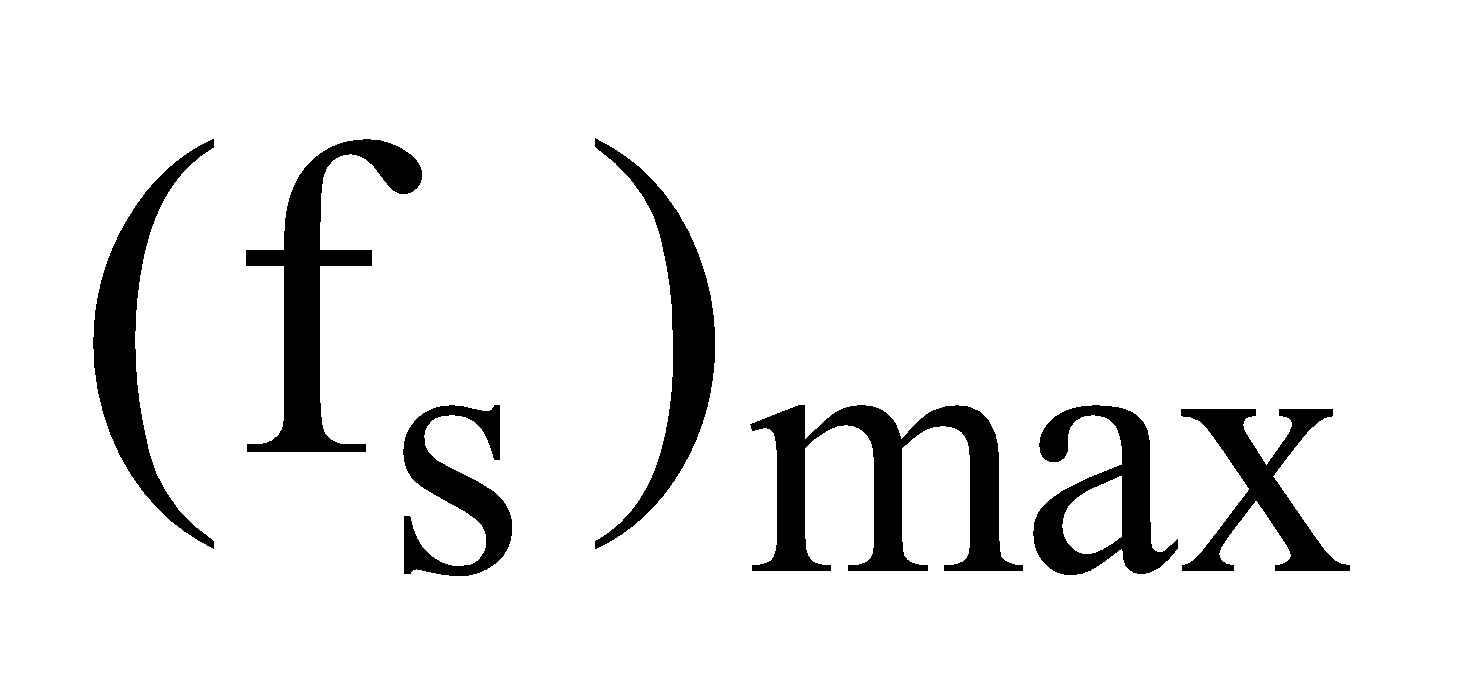
Fig.(c) 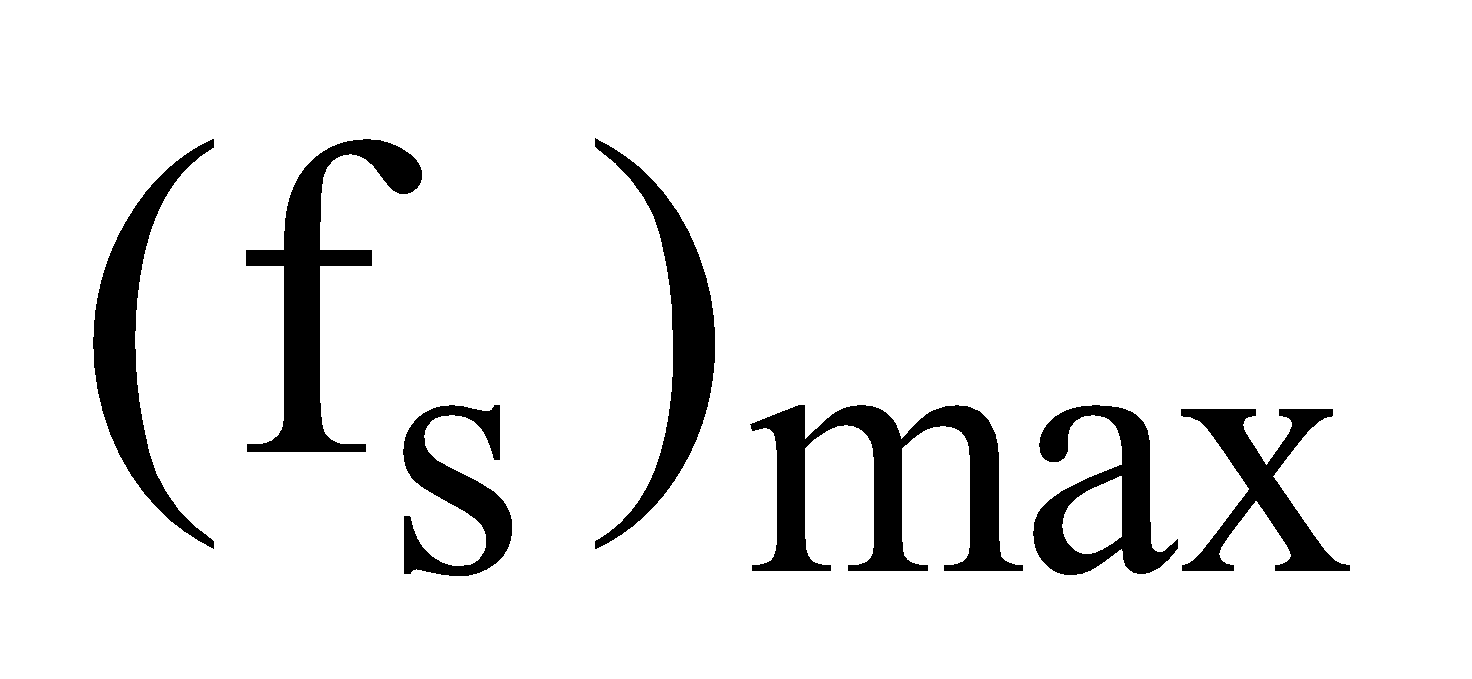 is equal to μkN. When the book is in motion, we call the retarding frictional force as the force of kinetic friction fk.
is equal to μkN. When the book is in motion, we call the retarding frictional force as the force of kinetic friction fk.
Since fk<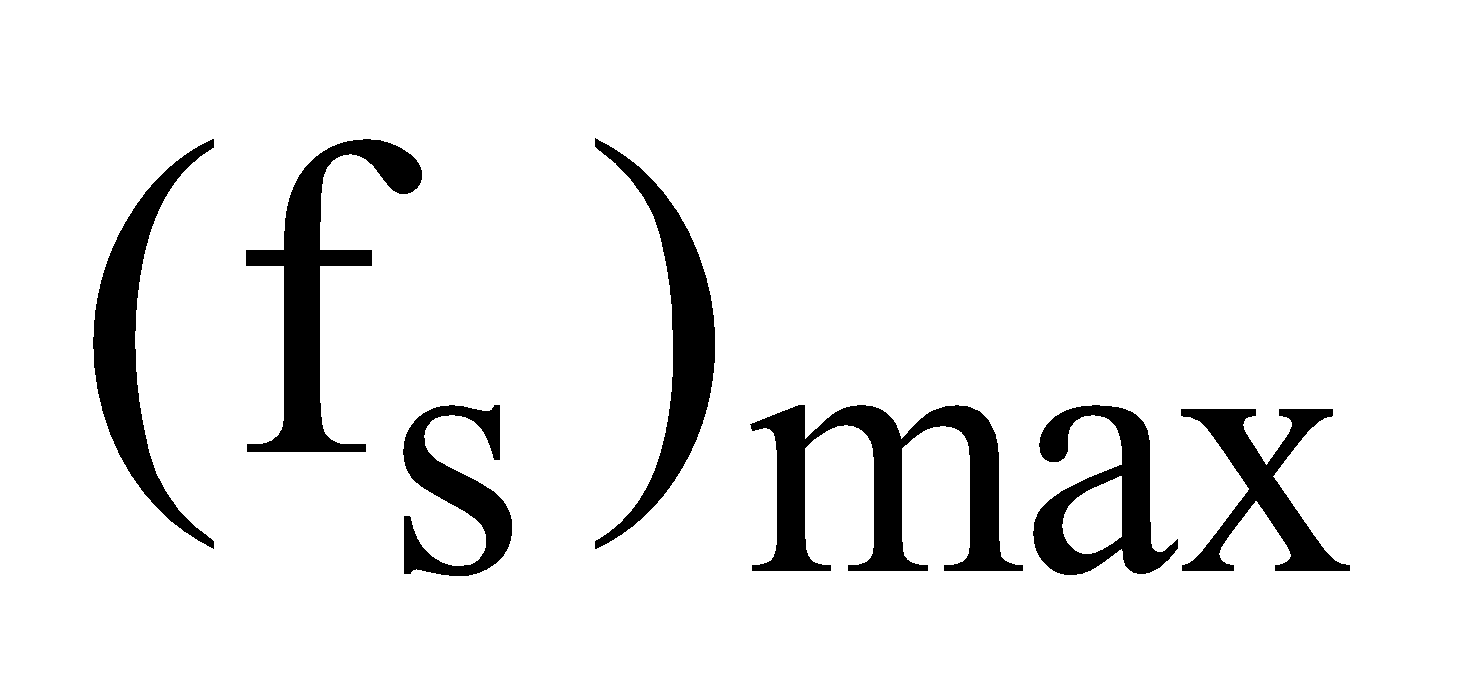 , so it is clear that we require more force to start motion than to maintain it against friction.
, so it is clear that we require more force to start motion than to maintain it against friction.
By experiment one can find that 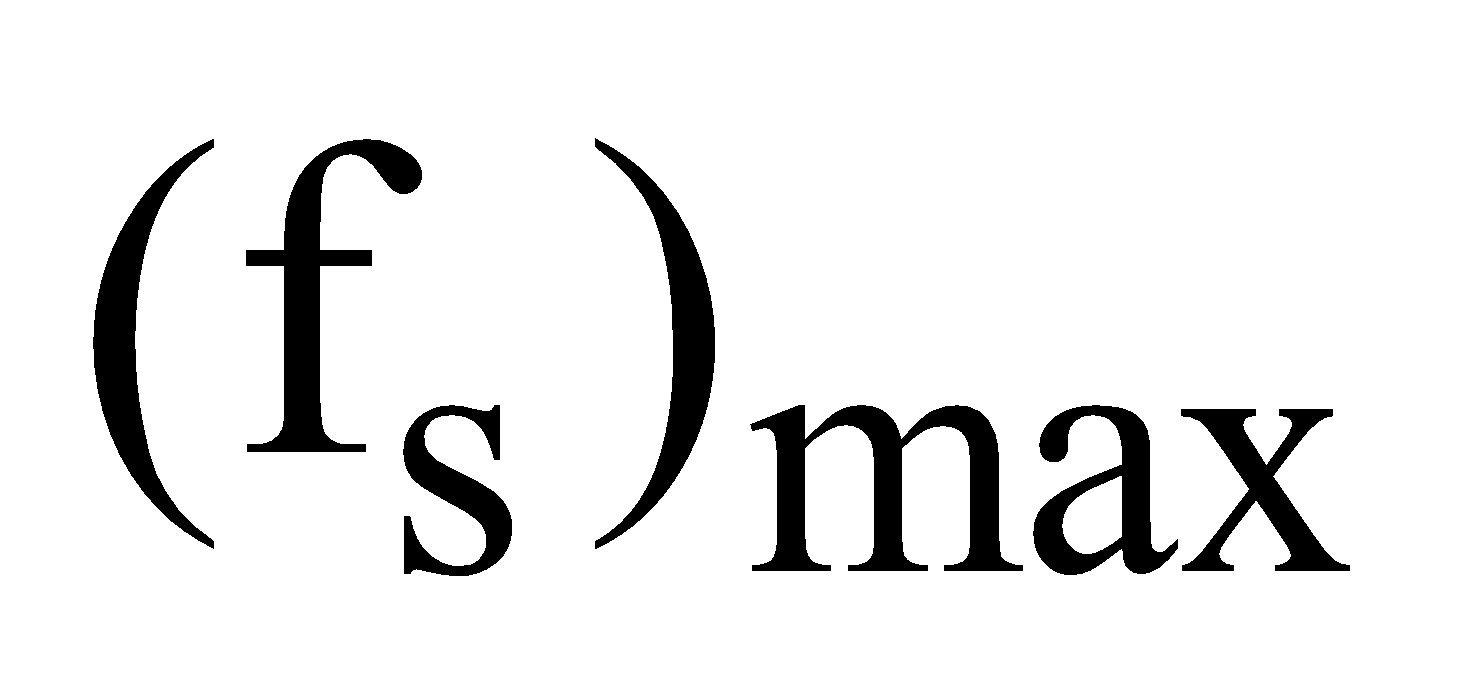 and fk are proportional to normal force N acting on the book (by rough surface) and depends on the roughness of the two surfaces in contact.
and fk are proportional to normal force N acting on the book (by rough surface) and depends on the roughness of the two surfaces in contact.
Note :
- The force of static friction between any two surfaces in contact is opposite to
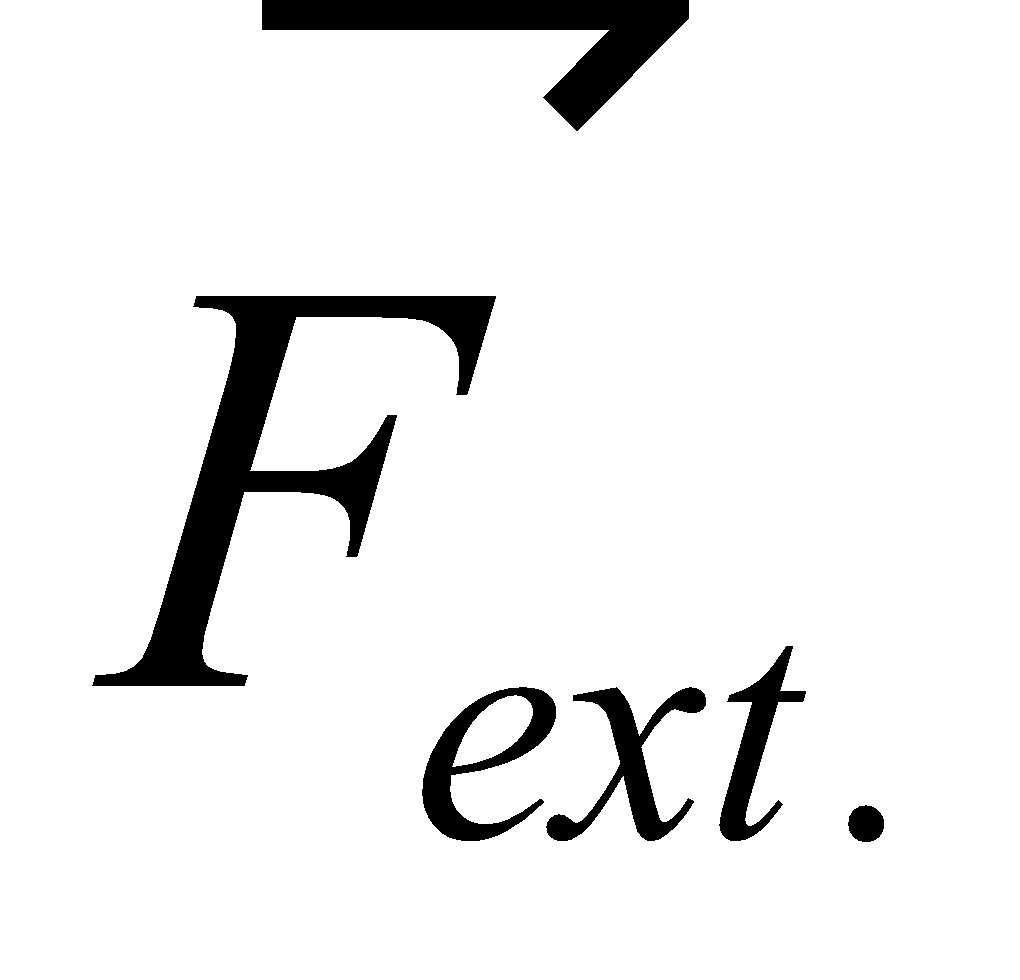 and given by
and given by 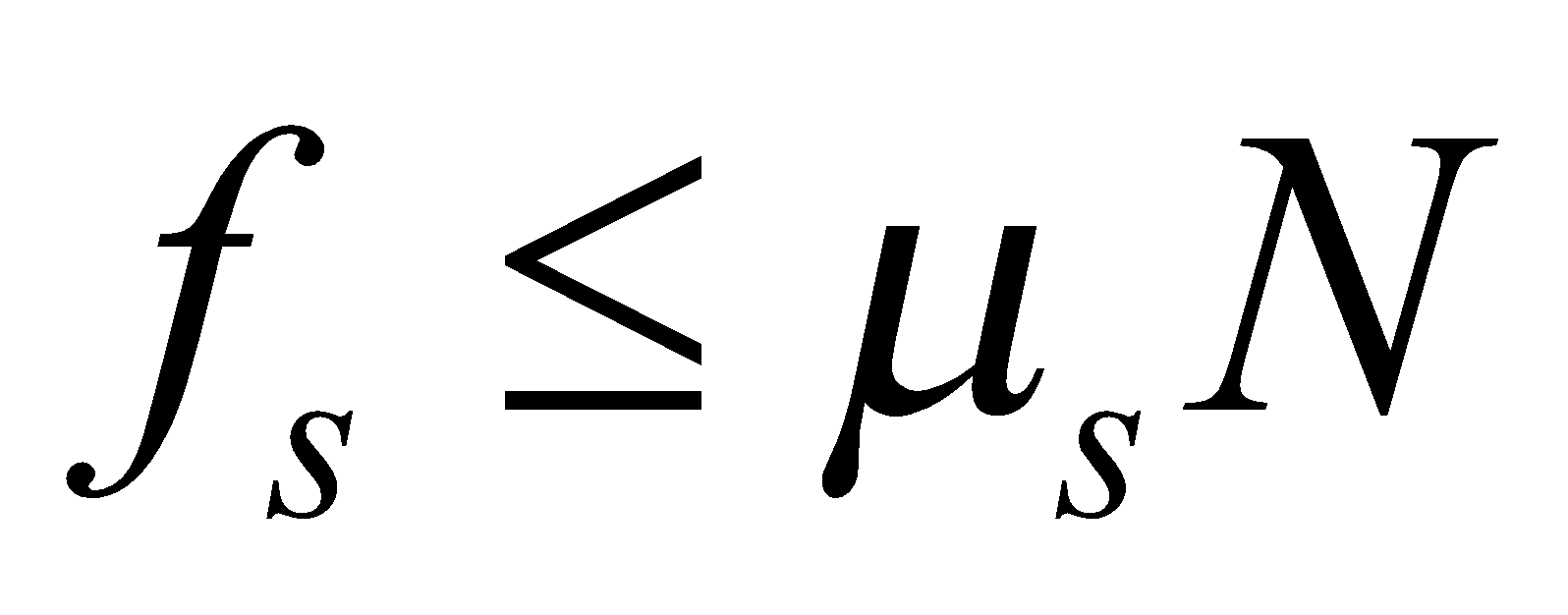 and
and 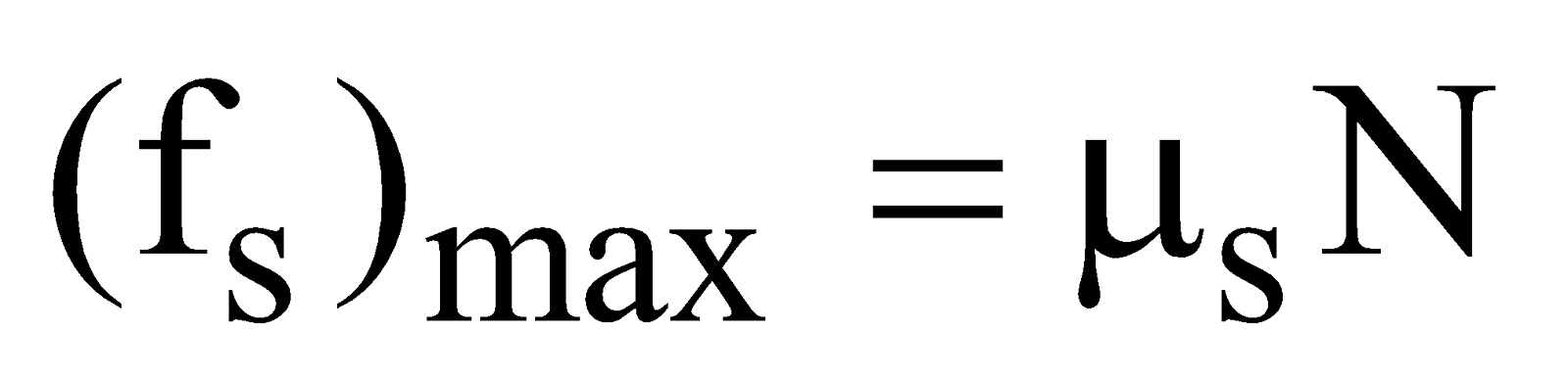 (when the body just moves in the right direction).
(when the body just moves in the right direction).
where N = W = weight of book and μs is called coefficient of static friction, fs is called force of static friction and is called limiting friction or maximum value of static friction.
- The force of kinetic friction is opposite to the direction of motion and is given by fk = μkN
where μk is coefficient of kinetic friction. - The value of μk and μs depends on the nature of surfaces and μk is always less then μs.
FRICTION ON AN INCLINED PLANE
Now we consider a book on an inclined plane & it just moves or slips, then by definition
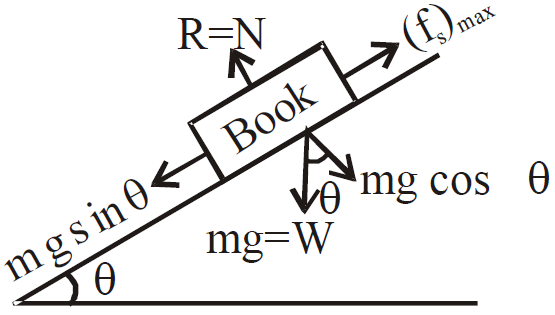
Now from figure,  and R = mg cosθ
and R = mg cosθ
where angle θ is called the angle of friction or angle of repose
SOME FACTS ABOUT FRICTION
- The force of kinetic friction is less than the force of static friction and the force of rolling friction is less than force of kinetic friction i.e.,
fr < fk < fs or μrolling < μkinetic < μstatic
hence it is easy to roll the drum in comparison to sliding it.
- Frictional force does not oppose the motion in all cases, in fact in some cases the body moves due to it.
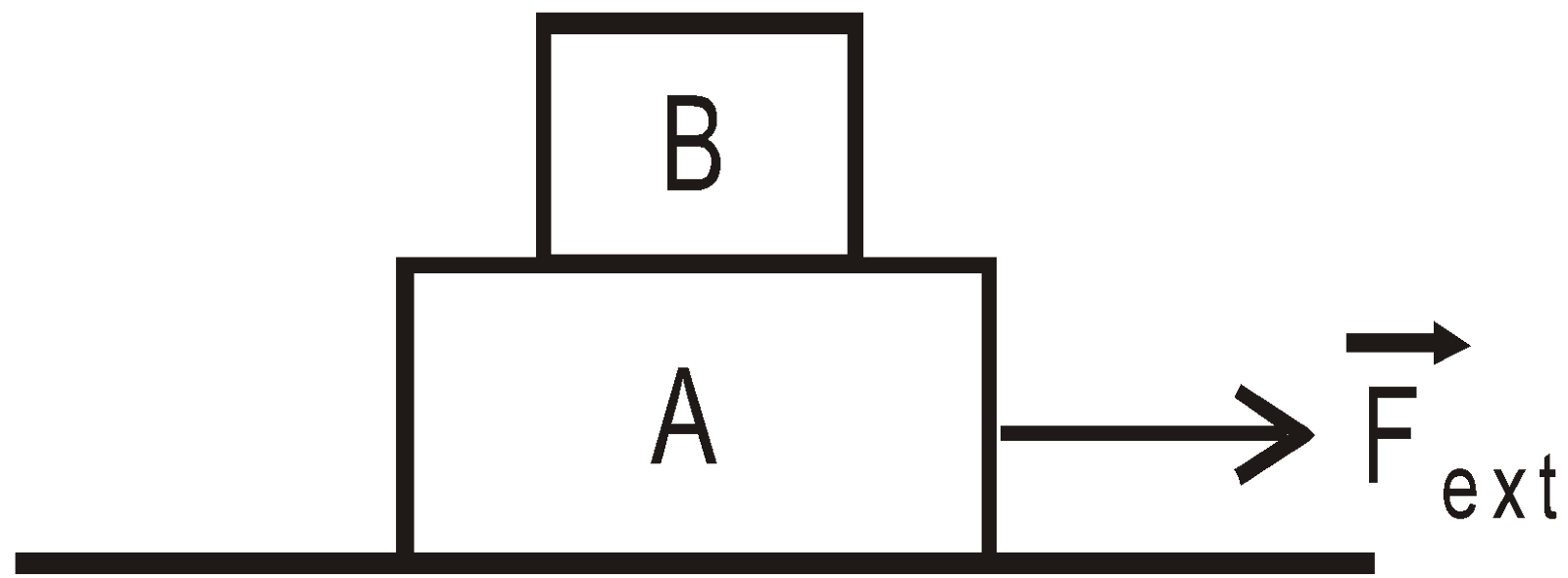
In the figure, book B moves to the right due to friction between A and B. If book A is totally smooth (i.e., frictionless) then book B does not move to the right. This is because of no force applies on the book B in the right direction.
LAWS OF LIMITING FRICTION
- The force of friction is independent of area of surfaces in contact and relative velocity between them (if it is not too high).
- The force of friction depends on the nature of material of surfaces in contact (i.e., force of adhesion). μ depends upon nature of the surface. It is independent of the normal reaction.
- The force of friction is directly proportional to normal reaction i.e., F ∝ N or F = mn.
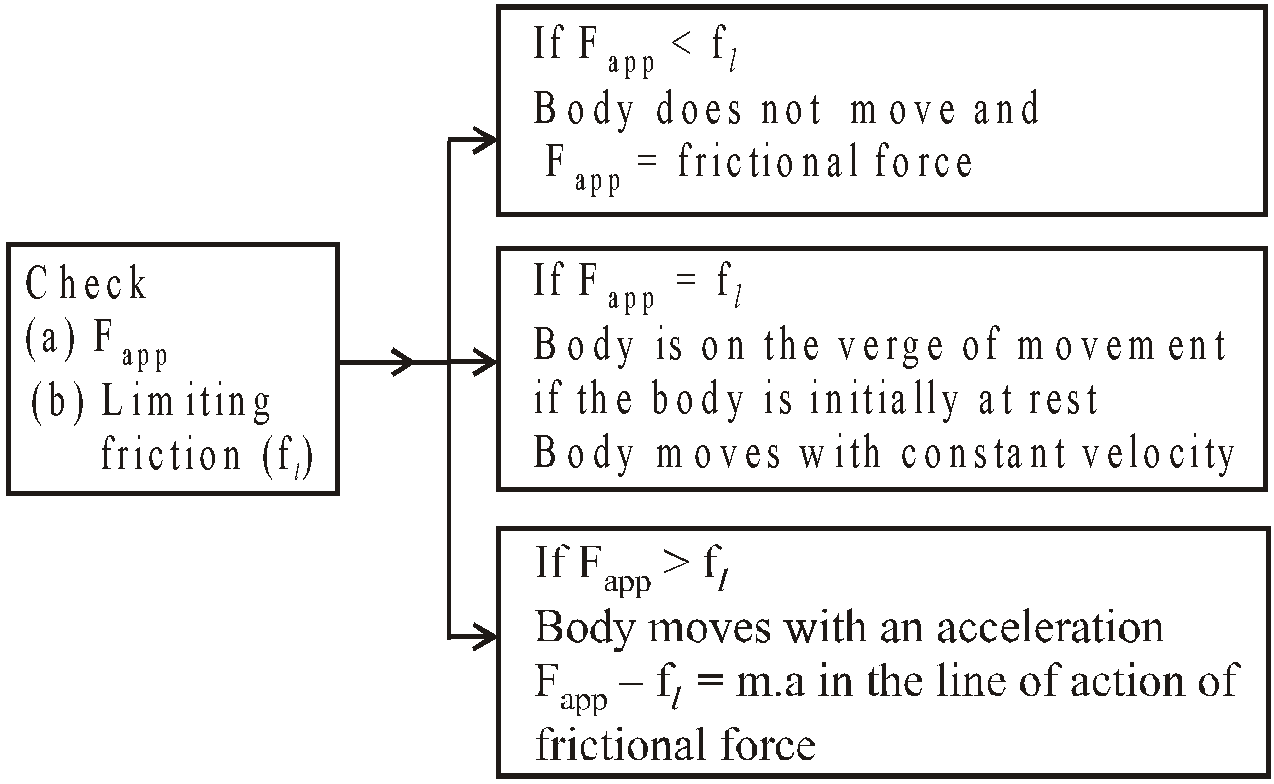
While solving a problem having friction involved, follow the given methodology

ROLLING FRICTION
The name rolling friction is a misnomer. Rolling friction has nothing to do with rolling. Rolling friction occurs during rolling as well as sliding operation.

CAUSE OF ROLLING FRICTION
When a body is kept on a surface of another body it causes a depression (an exaggerated view shown in the figure). When the body moves, it has to overcome the depression. This is the cause of rolling friction.
Note:- Rolling friction will be zero only when both the bodies in contact are rigid. Rolling friction is very small as compared to sliding friction. Work done by rolling friction is zero.
CONSERVATIVE AND NON-CONSERVATIVE FORCES
If work done on a particle is zero in complete round trip, the force is said to be conservative. The gravitational force, electrostatics force, elastic force etc., are conservative forces. On the other hand if the work done on a body is not zero during a complete round trip, the force is said to be non-conservative. The frictional force, viscous force etc. are non-conservative forces.
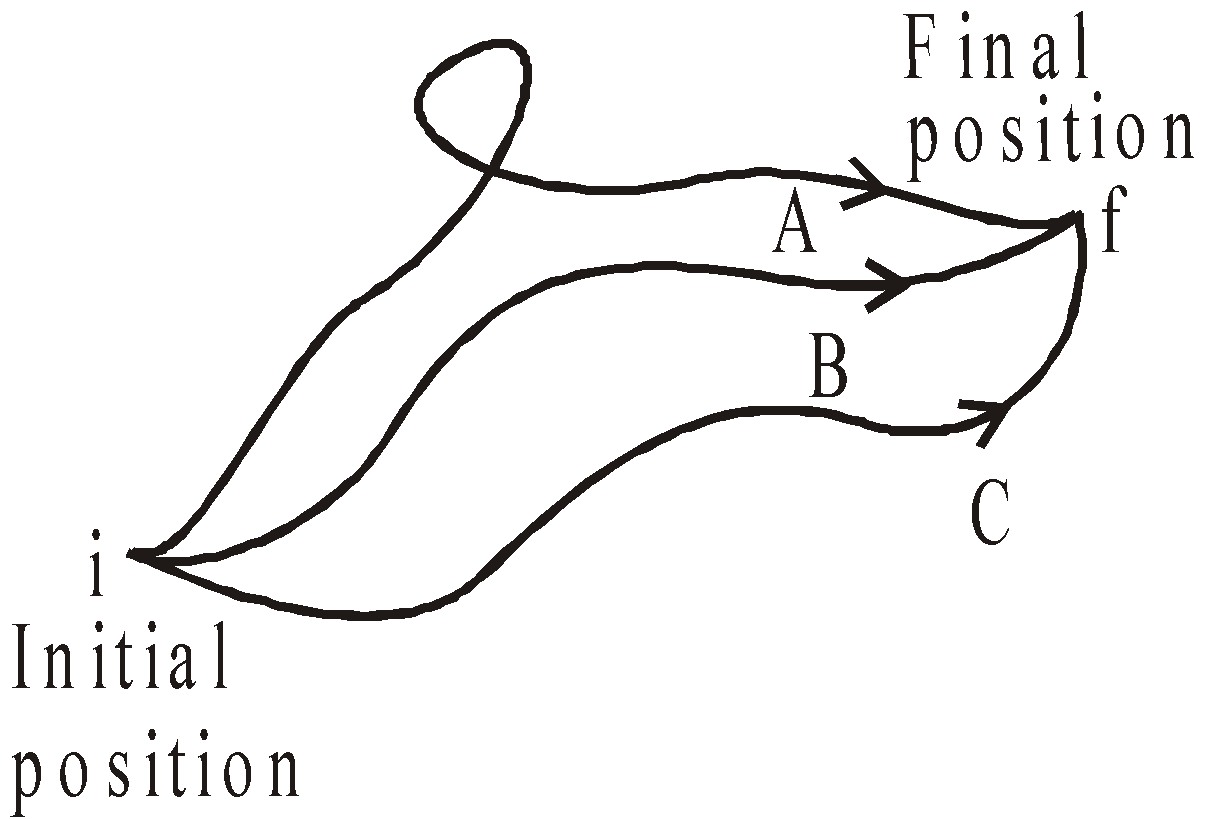
Figure shows three processes A, B and C by which we can reach from an initial position to final position. If force is conservative, then work done is same in all the three processes i.e., independent of the path followed between initial and final position. If force is non conservative then work done from i to f is different in all three paths A, B and C.
Hence it is clear that work done in conservative force depends only on initial & final position irrespective of the path followed between initial & final position. In case of non-conservative forces the work done depends on the path followed between initial and final position.
We can say also that there is no change in kinetic energy of the body in complete round trip in case of conservative force. While in case of non-conservative forces, when a body return to its initial position after completing the round trip, the kinetic energy of the body may be more or less than the kinetic energy with which it starts.
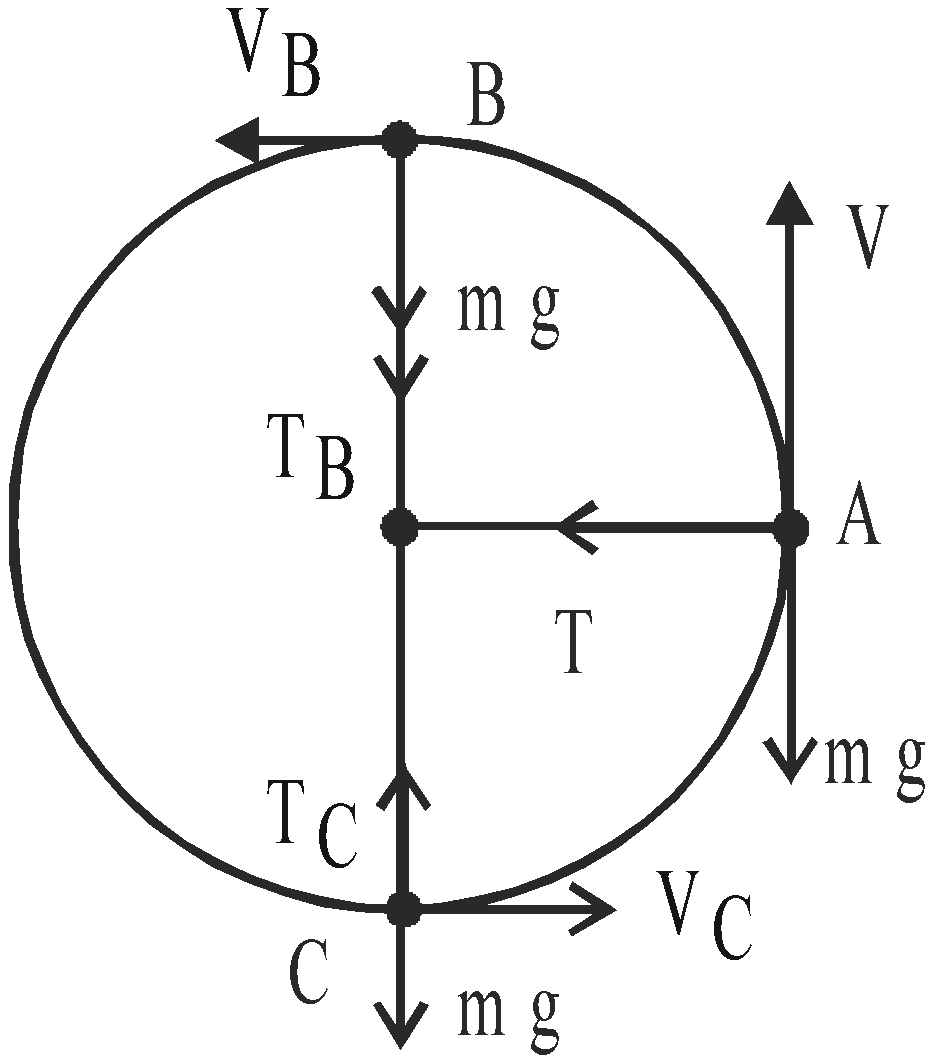
CASES OF CIRCULAR MOTIONS
MOTION IN A VERTICAL CIRCLE
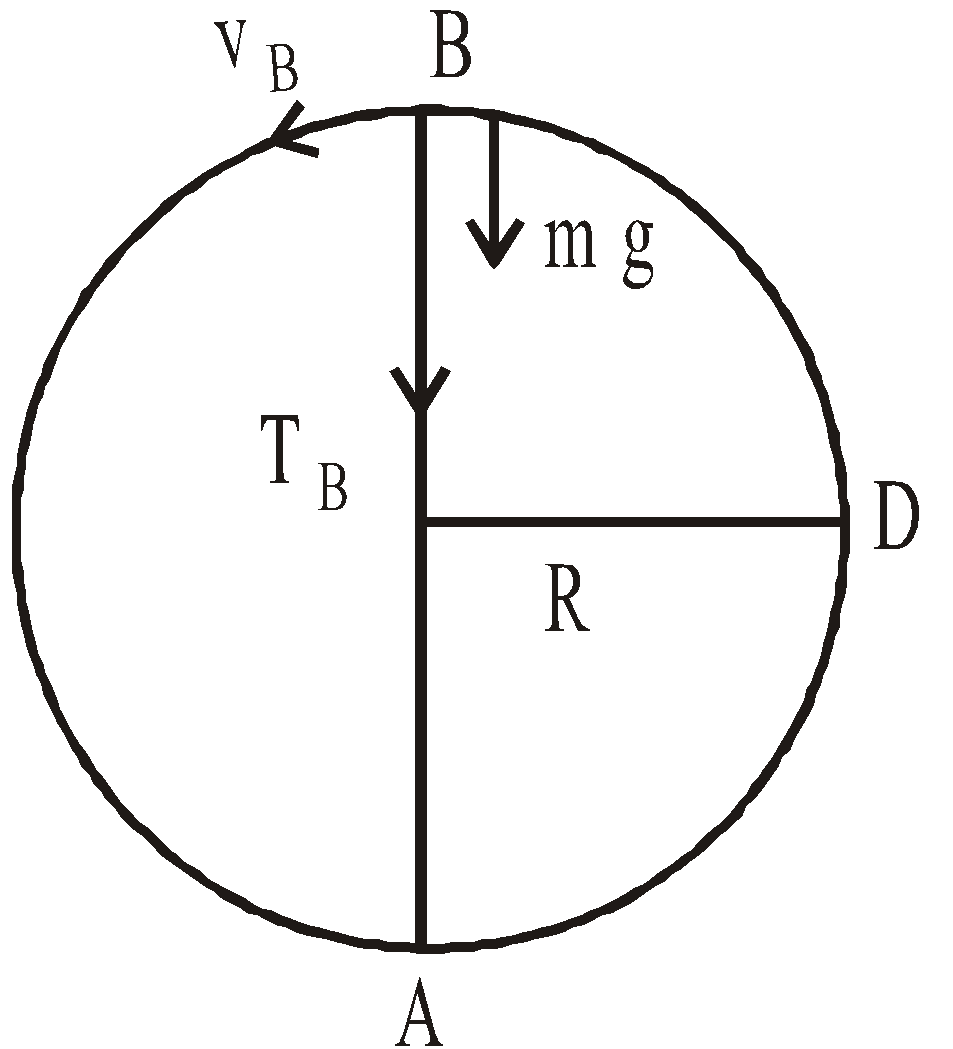
Let us consider a particle of mass m attached to a string of length R let the particle be rotated about its centre O.
At t = 0 the particle start with velocity u from the point A (lowest point of vertical circle) and at time t its position is P. Then the tension at point P is given by

So tension at point A (lowest point of vertical circle) is
and tension at point B (highest point of vertical circle) is
Where 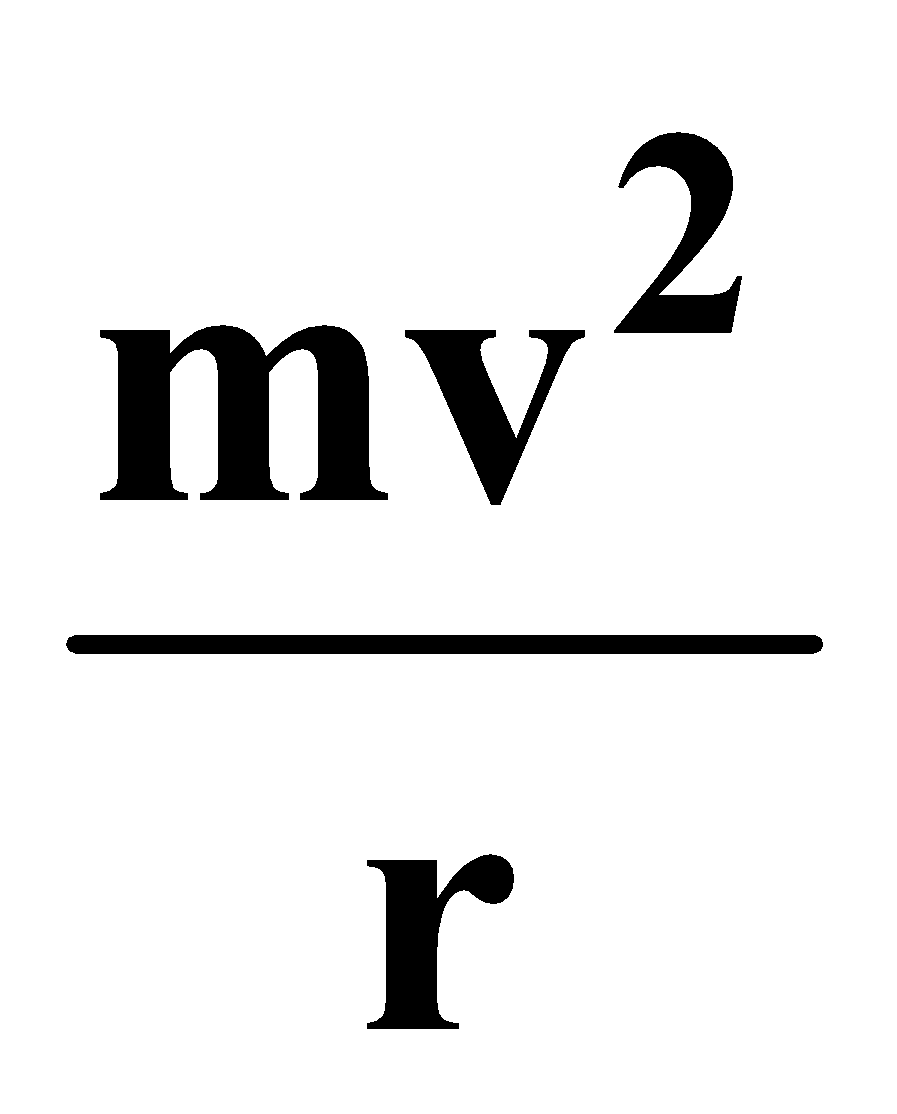 is centripetal force required for the particle to move in a vertical circle.
is centripetal force required for the particle to move in a vertical circle.
Now from law of conservation of energy
or, 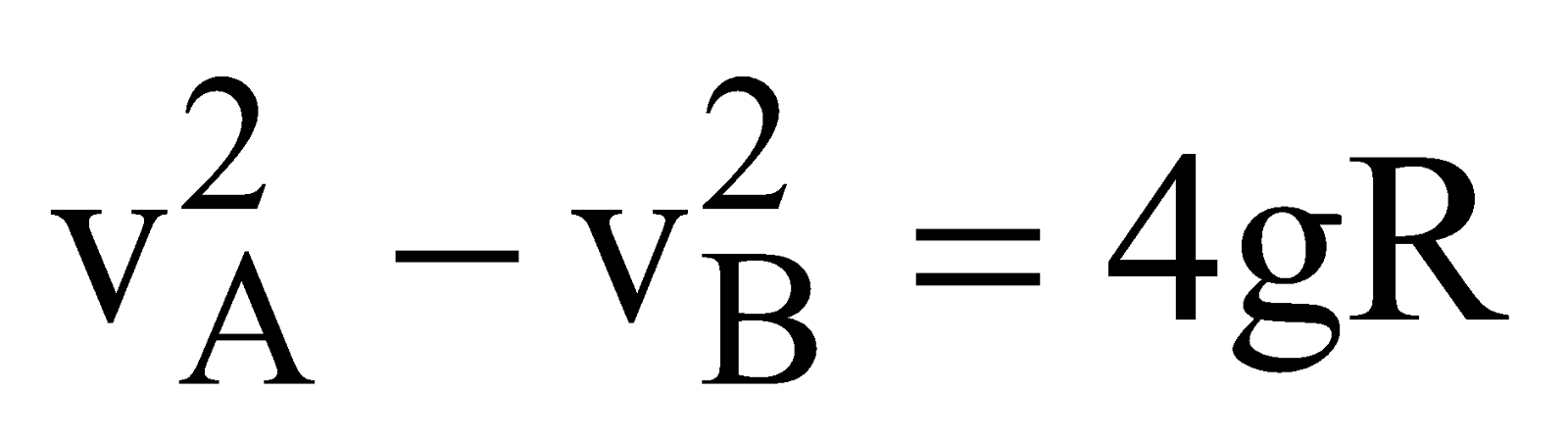 …(4)
…(4)
(change in kinetic energy of particle) = (change in potential energy of particle)
Or (loss in kinetic energy of the particle) = (gain in potential energy)
In conservative force system (such as gravity force) the mechanical energy (i.e., kinetic energy + potential energy) must be constant.
Total energy will be constant
Now from eqns.(2) and (3), we get

⇒ 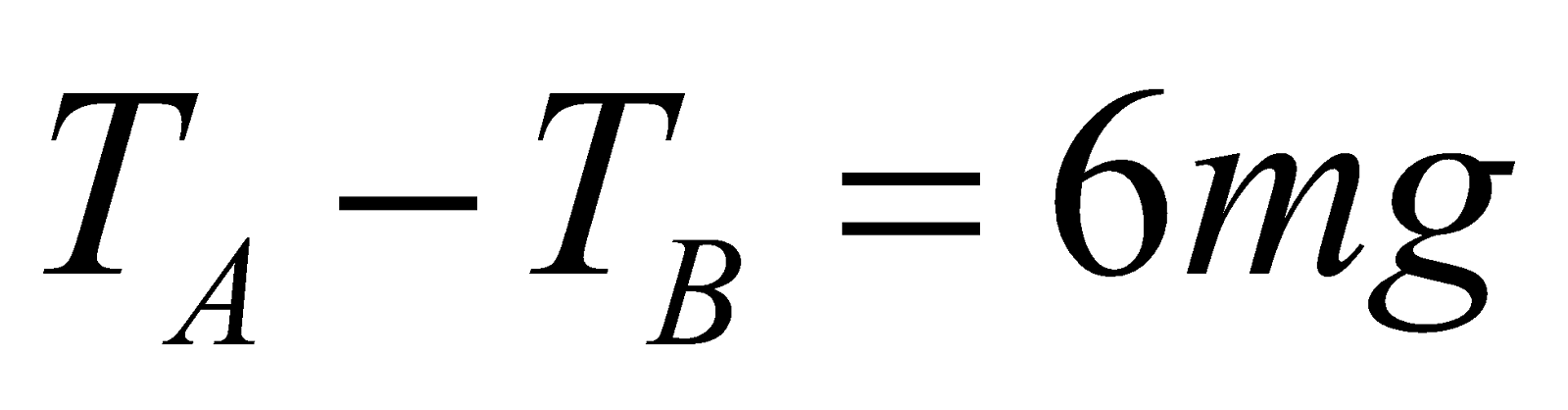 …(5)
…(5)
or TA = TB + 6mg …(6)
So it is clear from eqn. (6) that tension in string at lowest point of vertical circle is greater then the tension at highest point of vertical circle by 6mg.
CONDITION TO COMPLETE A VERTICAL CIRCLE
If we reduce the velocity vA in equation (2), then TA will be reduce and at some critical velocity vc, TB will be zero, then put TB = 0 and vB = vC in equation (3) and we obtain
In this condition the necessary centripetal force at point B is provided by the weight of the particle [see again equation (3)] then from equation (4), we get
then the tension at the point A will be
Hence if we rotate a particle in a vertical circle and tension in string at highest point is zero, then the tension at lowest point of vertical circle is 6 times of the weight of the particle.
SOME FACTS OF VERTICAL MOTION
- The body will complete the vertical circle if its velocity at lowest point is equal to or greater than
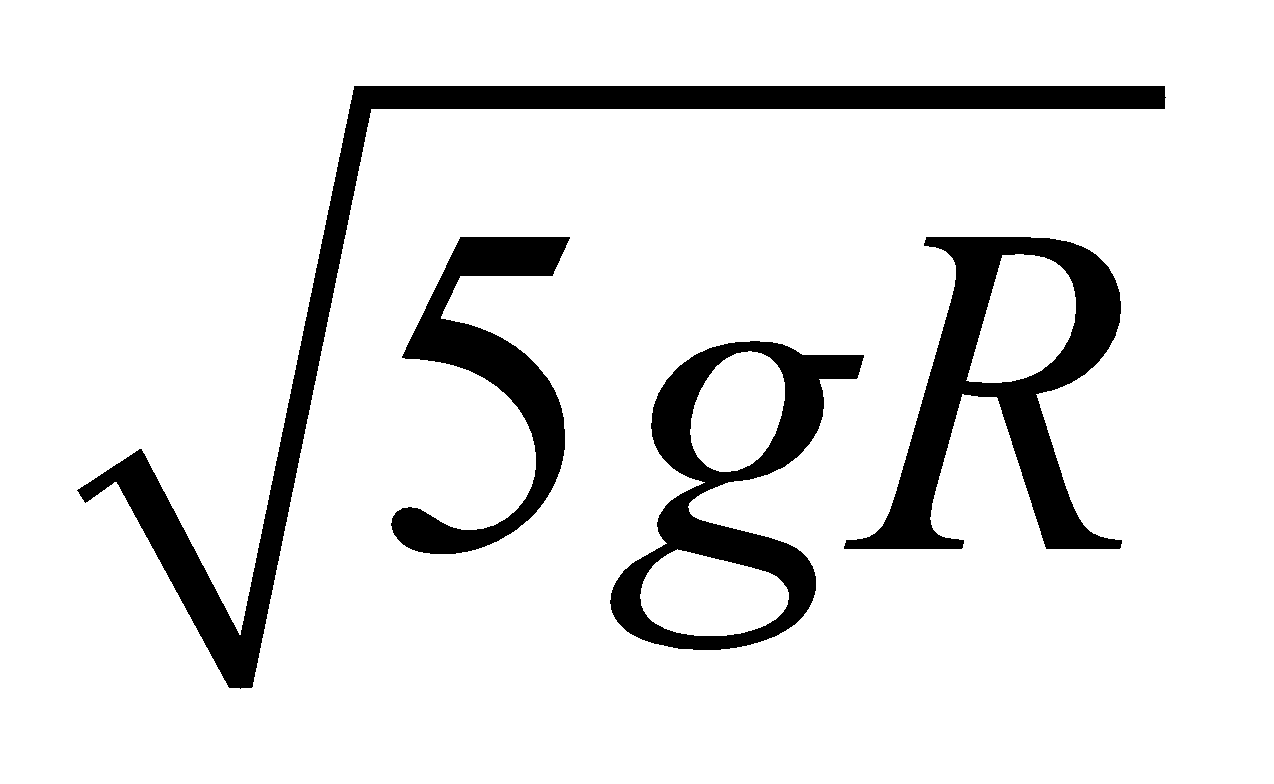
- The body will oscillate about the lowest point if its velocity at lowest point is less then
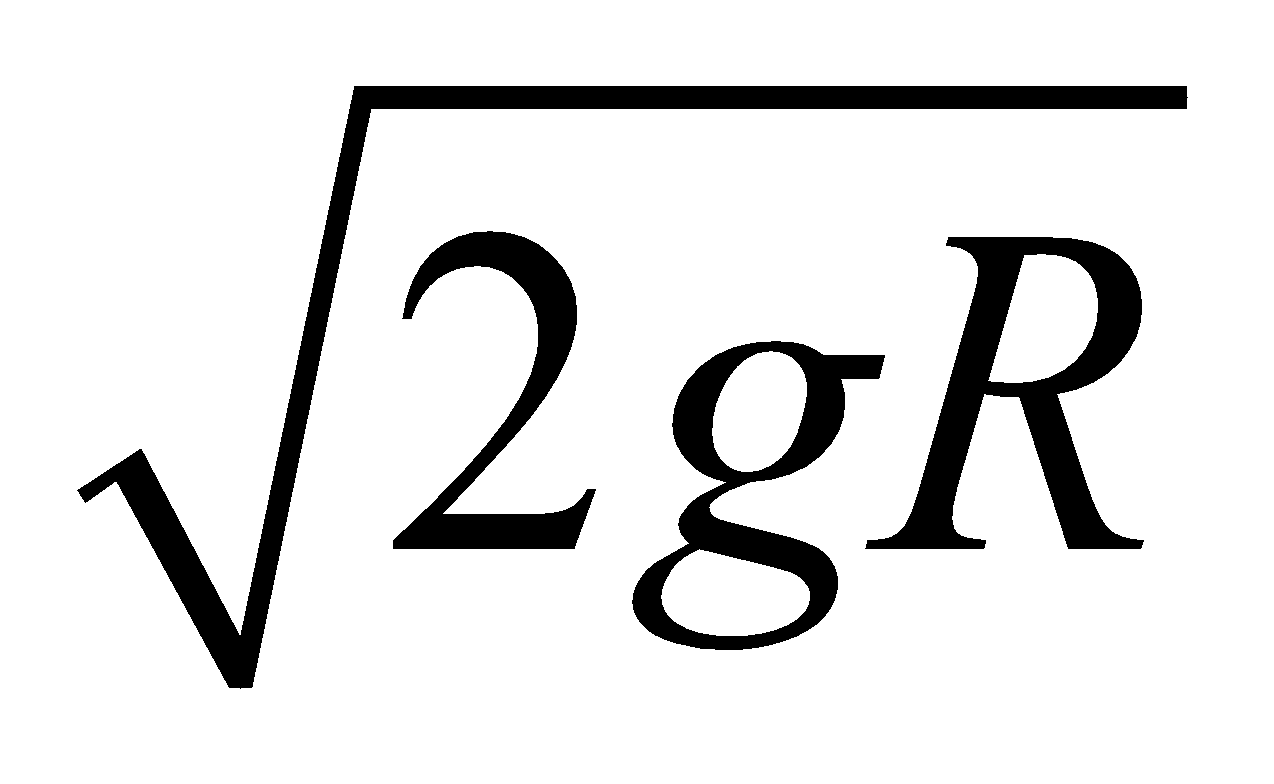 . This will happen when the velocity at the halfway mark, i.e.
. This will happen when the velocity at the halfway mark, i.e. 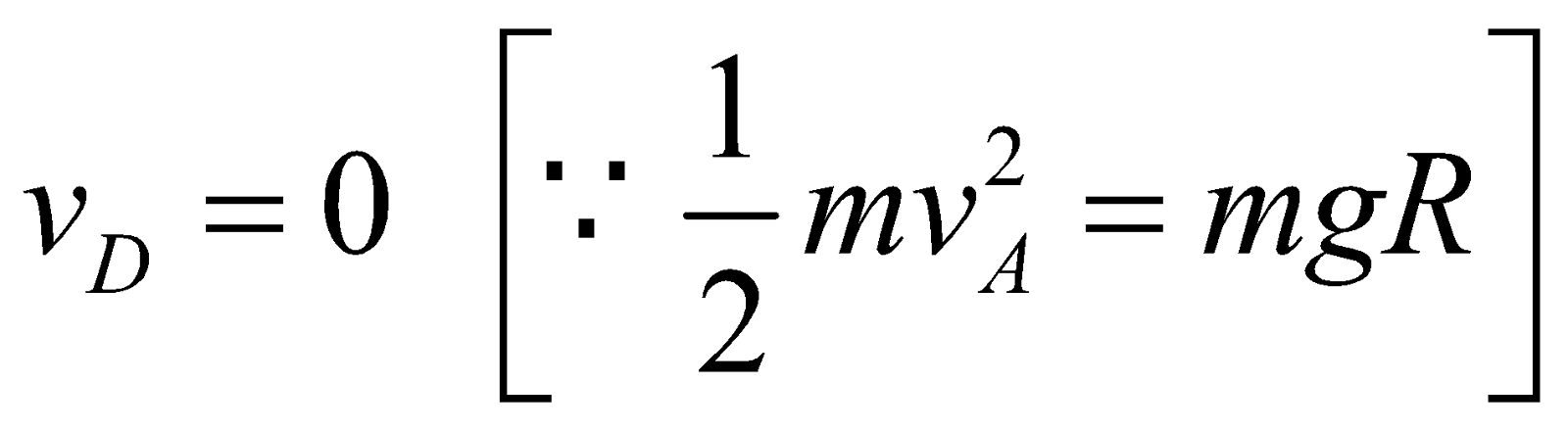
- The string become slack and fails to describe the circle when its velocity at lowest point lies between
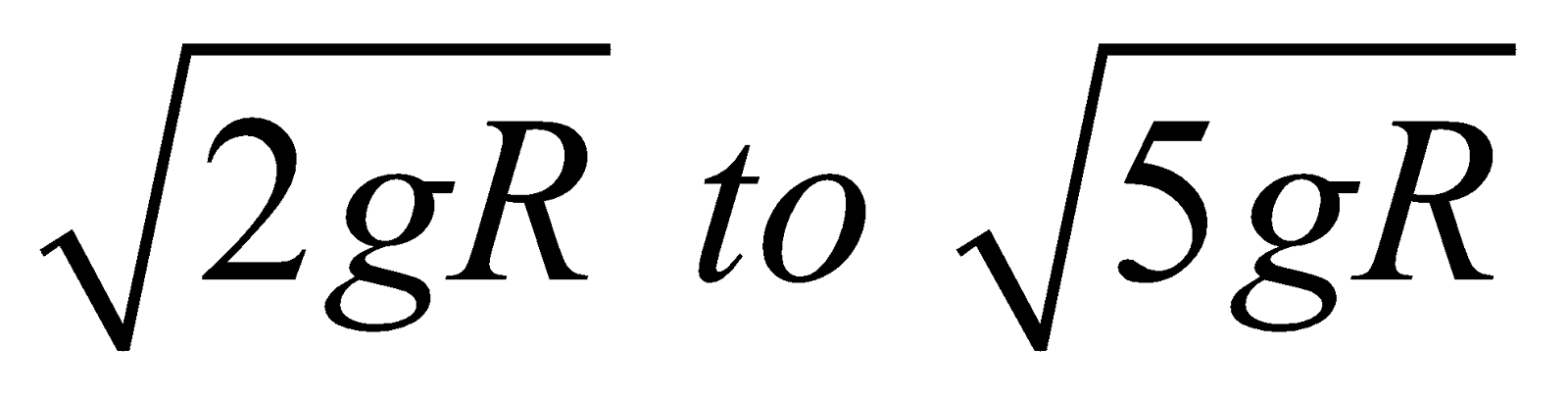
CASE OF CYCLIST
To safely negotiate a curve of radius r, a cyclist should bend at an angle θ with the vertical.
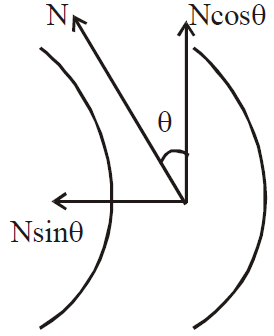
Which is given by tan θ = 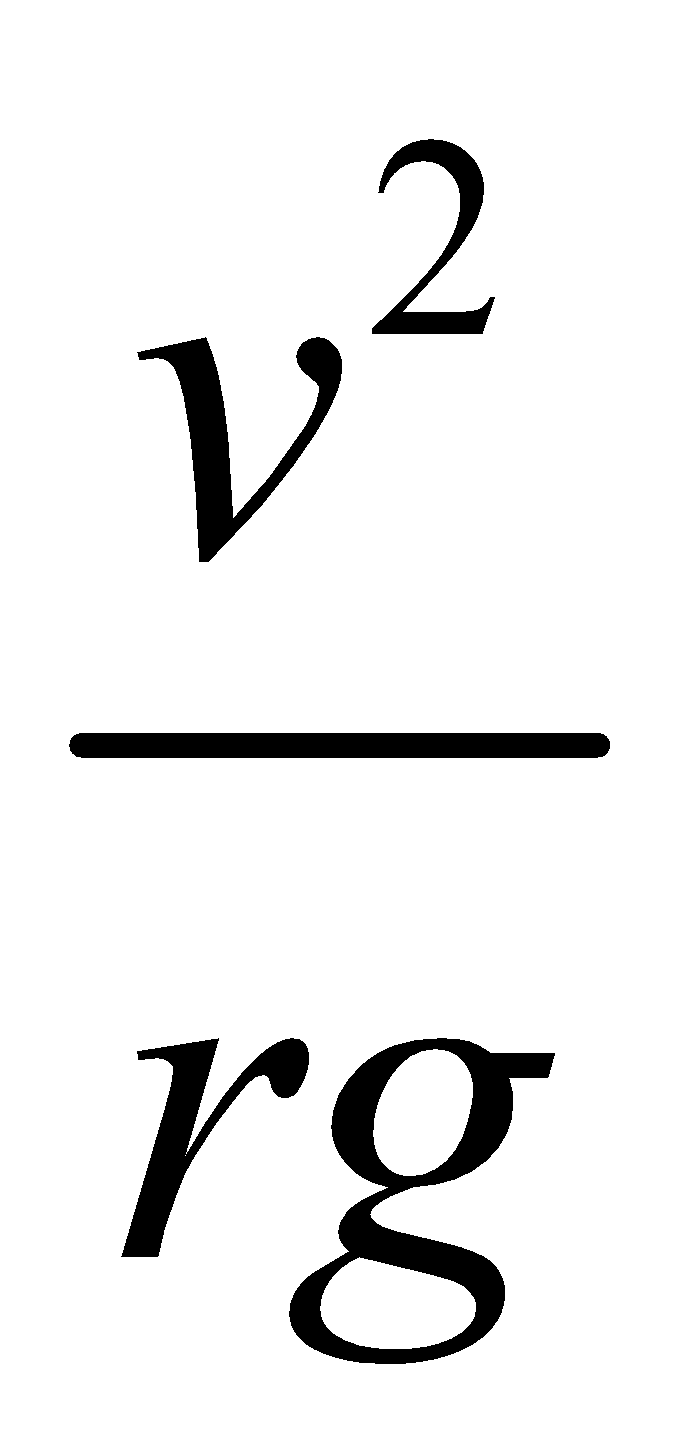 .
.
Angle θ is also called as angle of banking.
CASE OF CAR ON A LEVELLED ROAD
A vehicle can safely negotiate a curve of radius r on a rough level road when coefficient of sliding friction is related to the velocity as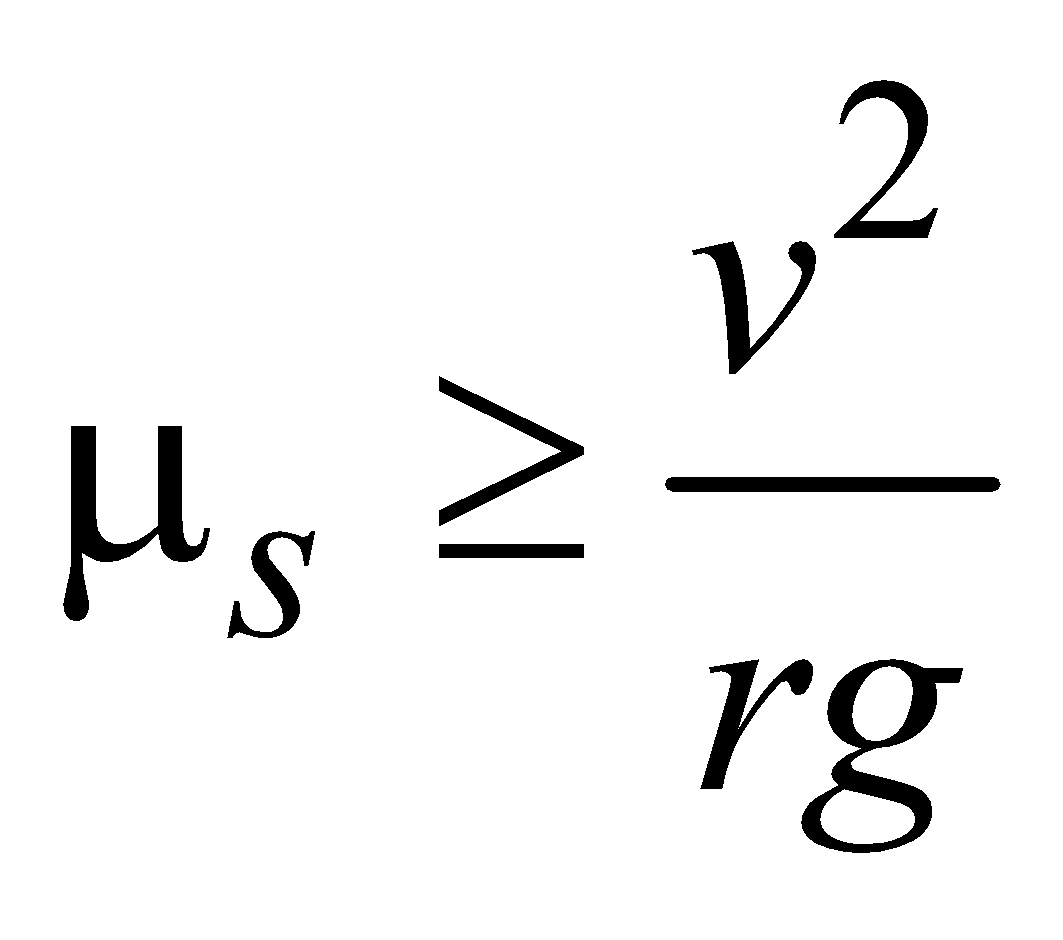 .
.
Now consider a case when a vehicle is moving in a circle, the centrifugal force is 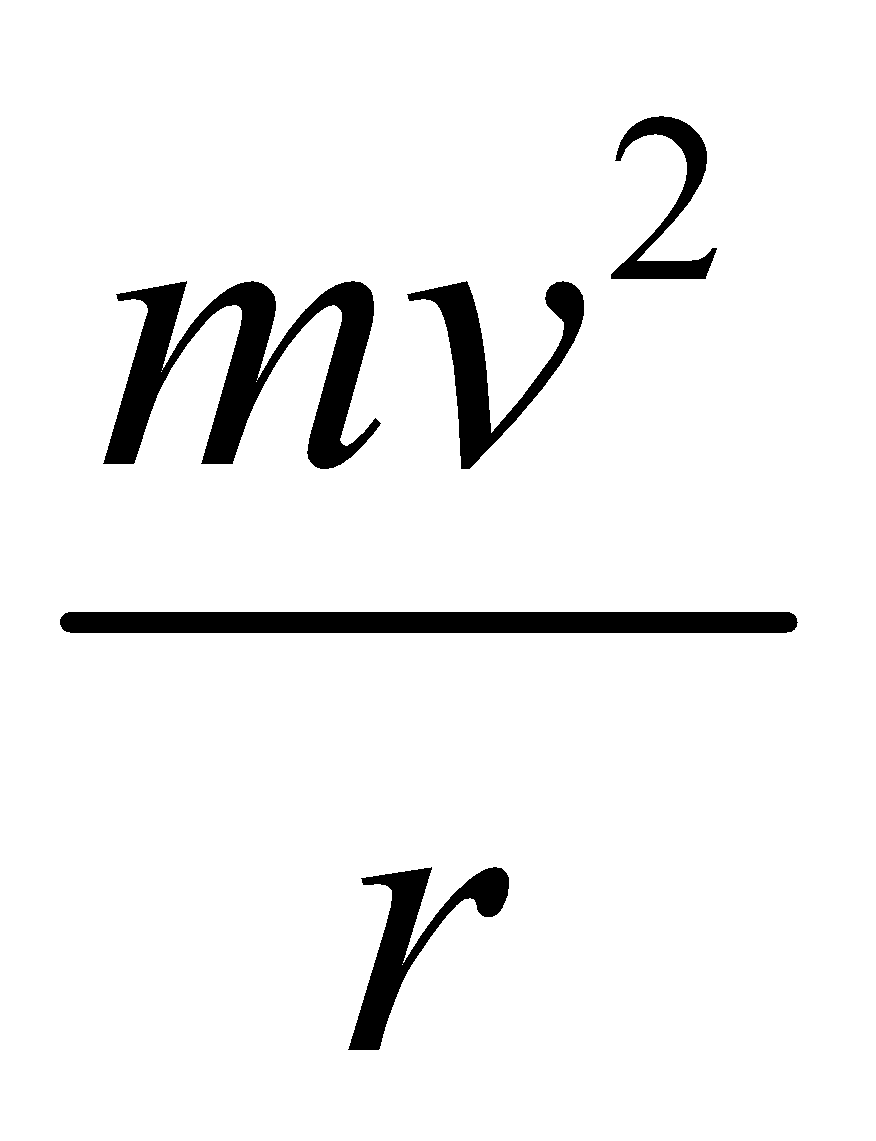 whereas m is mass of vehicle, r = radius of circle and v is its velocity.
whereas m is mass of vehicle, r = radius of circle and v is its velocity.

The frictional force is static since wheels are in rolling motion because point of contact with the surface is at rest
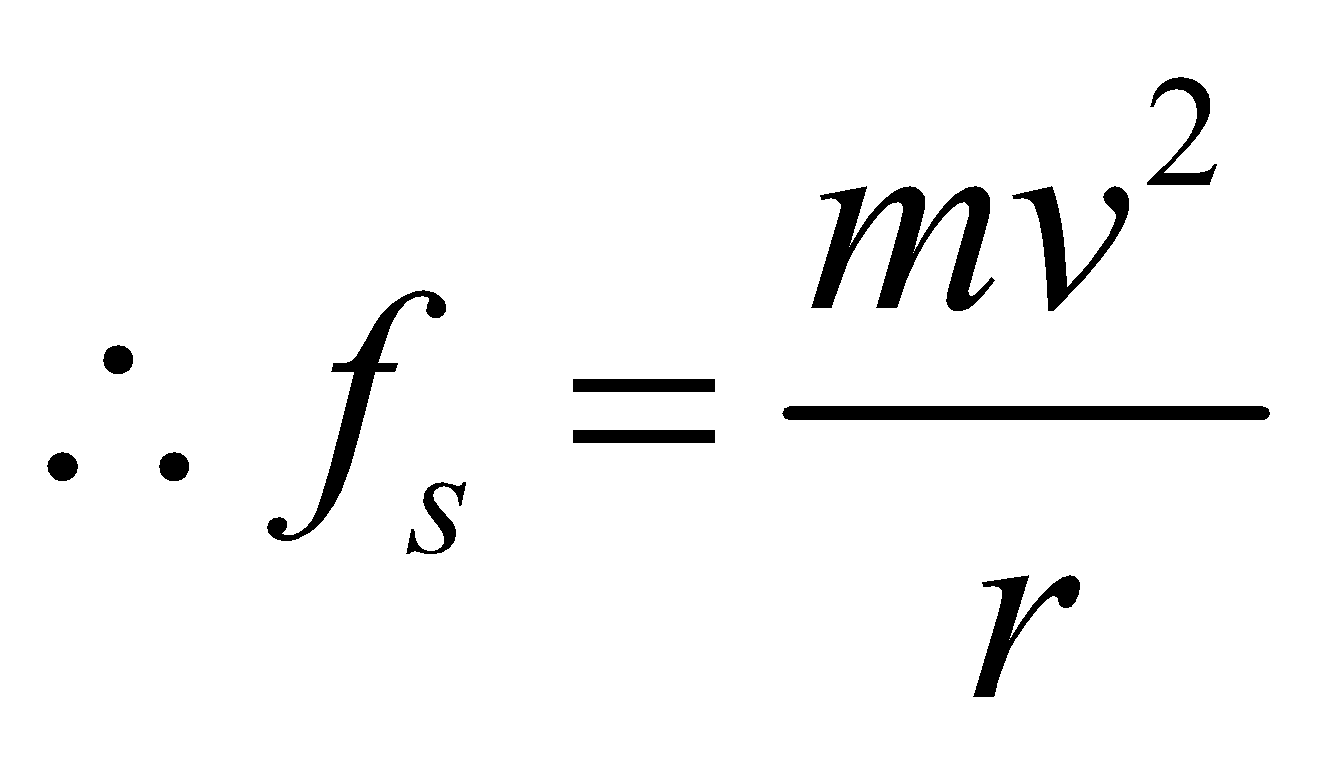
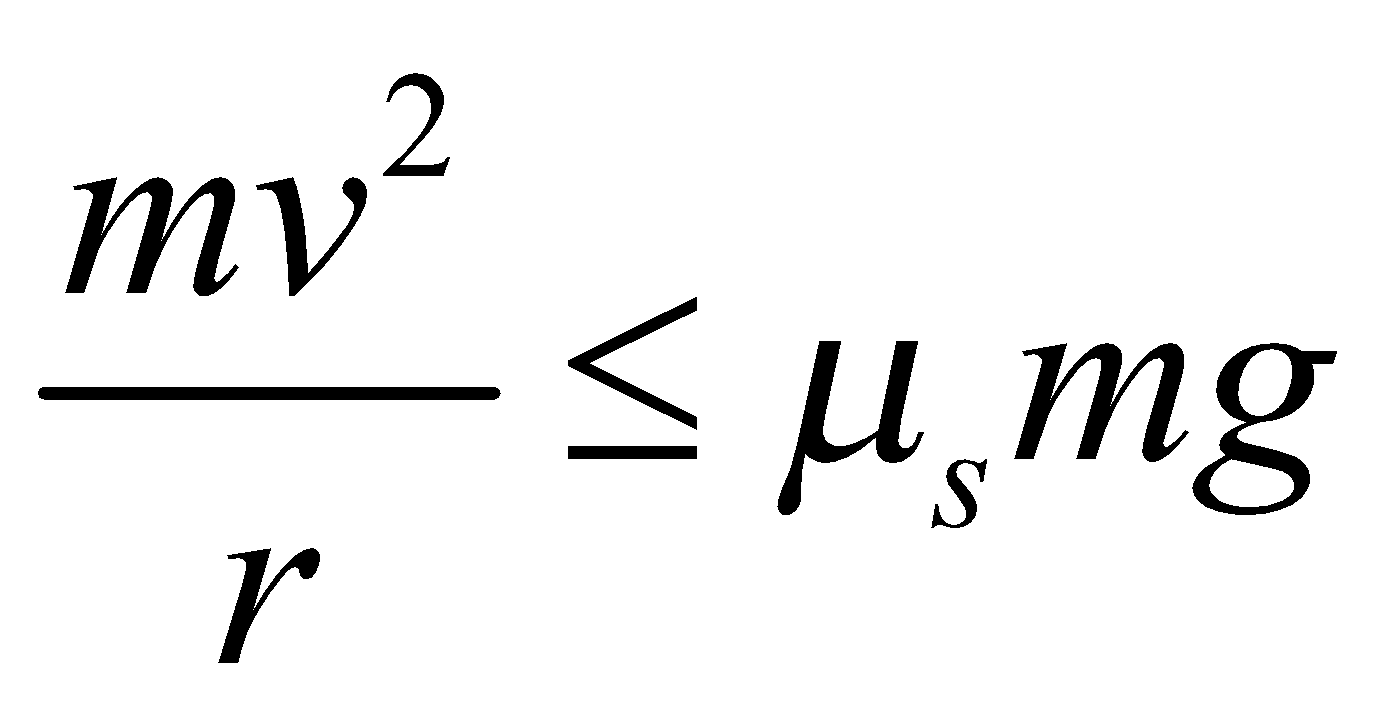 or
or 
CASE OF BANKING OF ROAD (FRICTIONLESS)
A vehicle can safely negotiate a curve of radius r on a smooth (frictionless) road, when the angle θ of banking of the road is given by
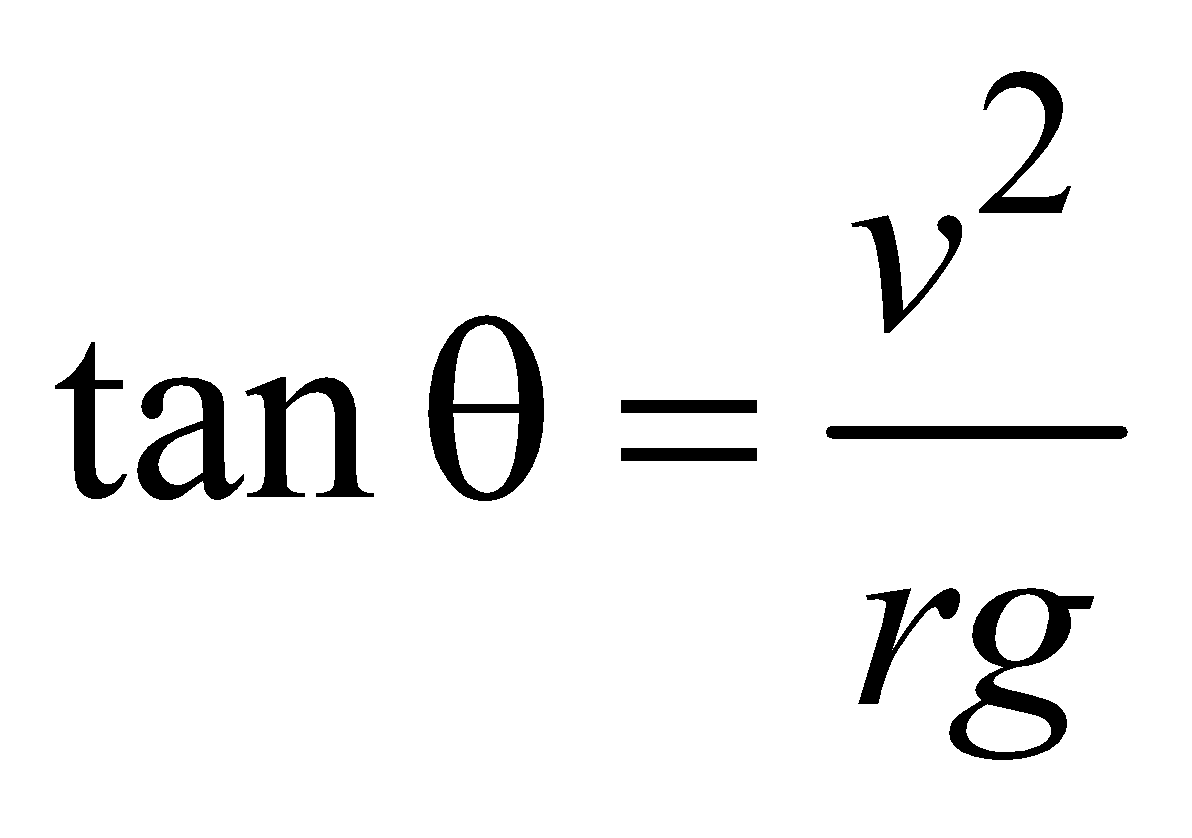

When the banked surface is smooth, the force acting will be gravity and normal force only.
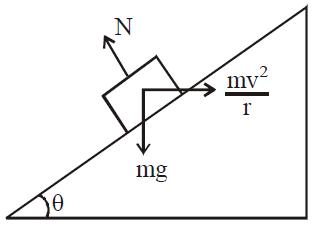
Balancing forces
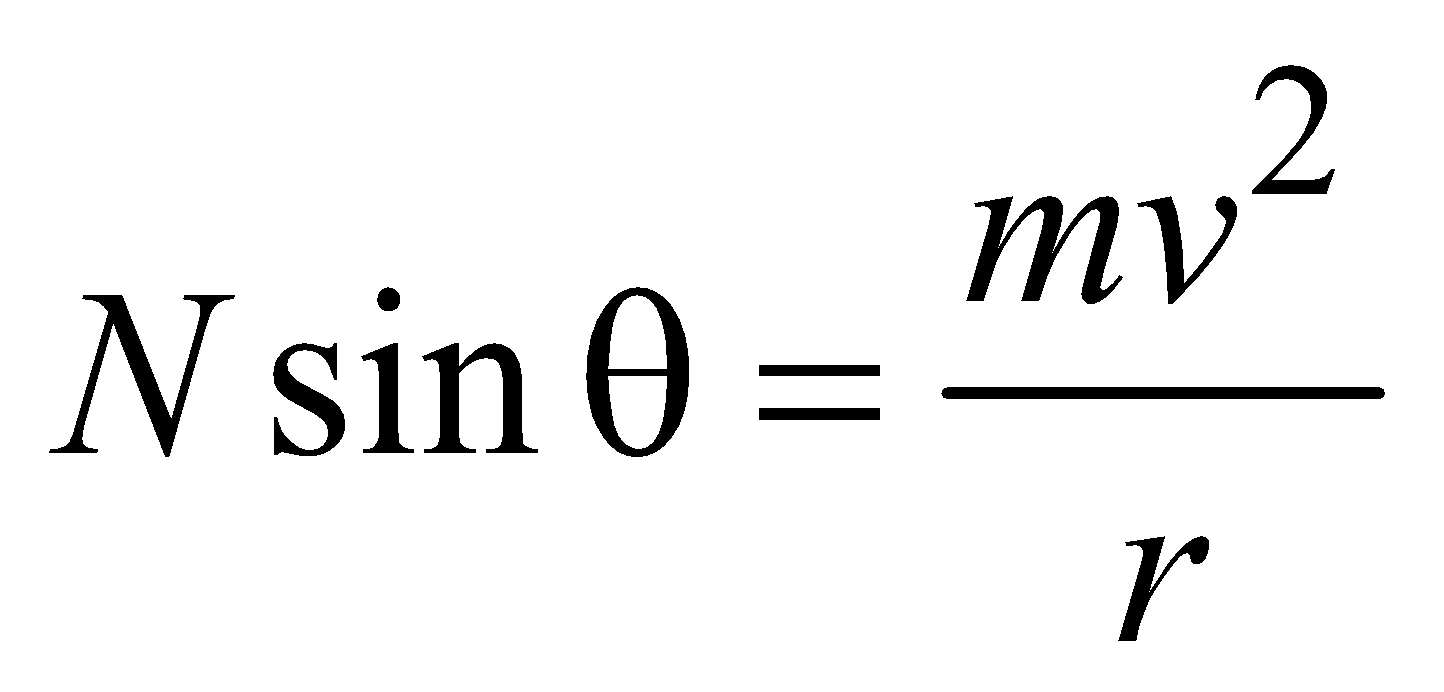 …(2)
…(2)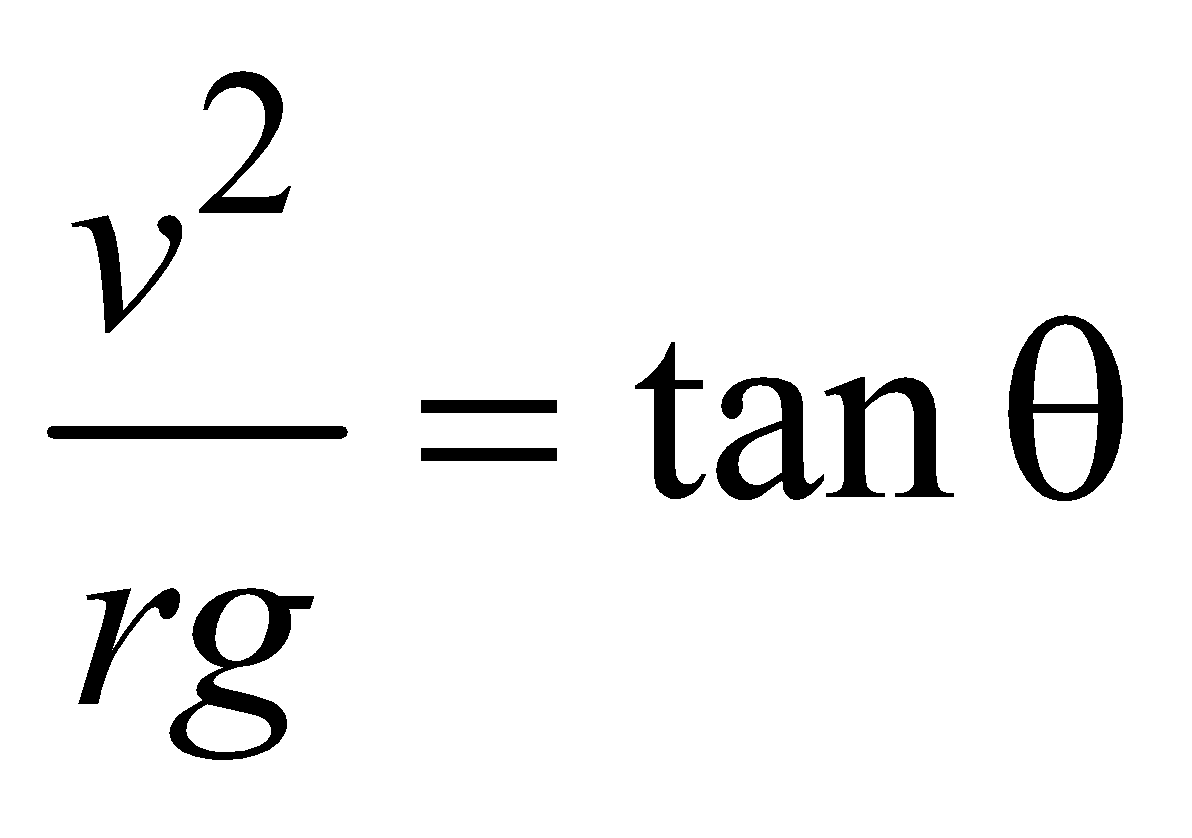 …(3)
…(3)CASE OF BANKING OF ROAD (WITH FRICTION)
The maximum velocity with which a vehicle can safely negotiate a curve of radius r on a rough inclined road is given by
v2 = 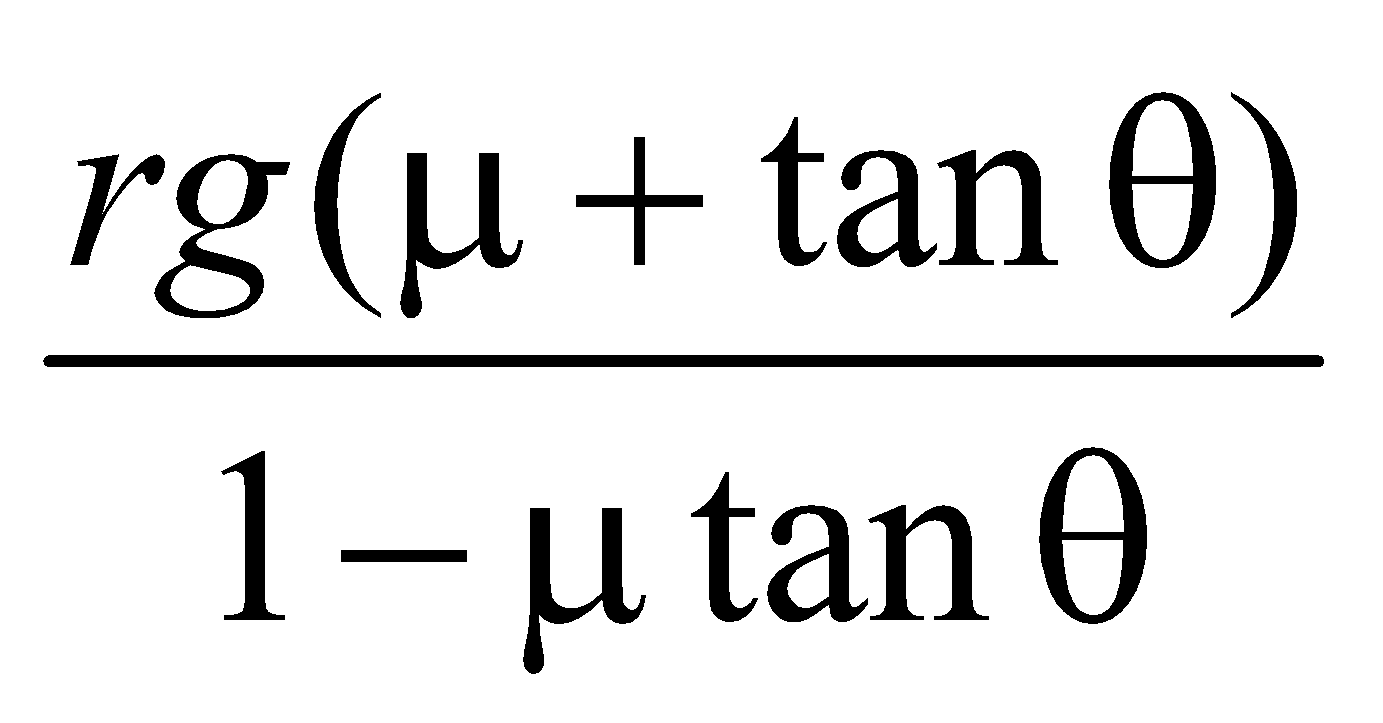
where μ is the coefficient of friction of the rough surface on which the vehicle is moving, and θ is the angle of inclined road with the horizontal.
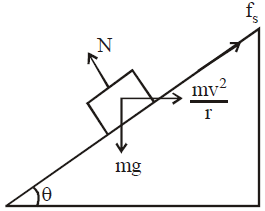
Suppose a vehicle is moving in a circle of radius r on a rough inclined road whose coefficient of friction is 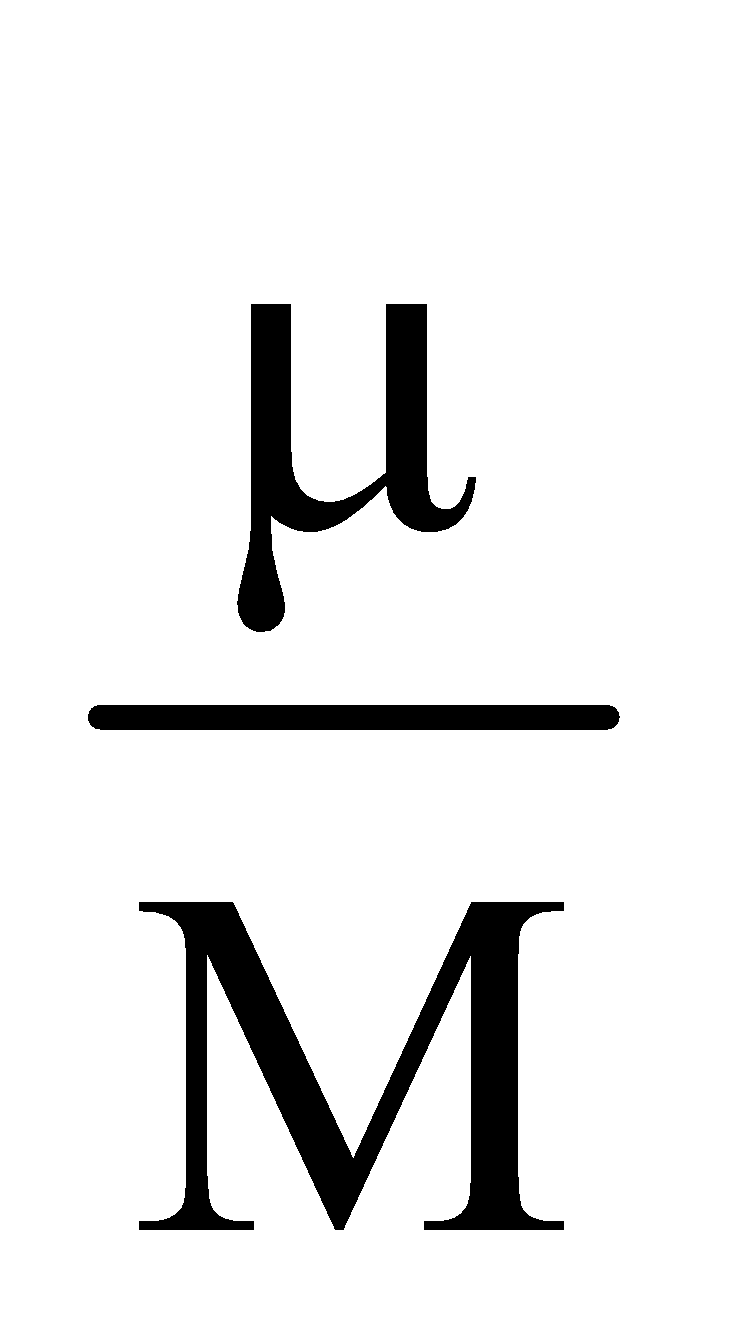 and angle of banking is θ.
and angle of banking is θ.
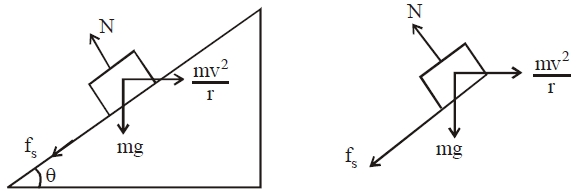
Let velocity of object (vehicle) be V.
If we apply pseudo force on body, centrifugal force is 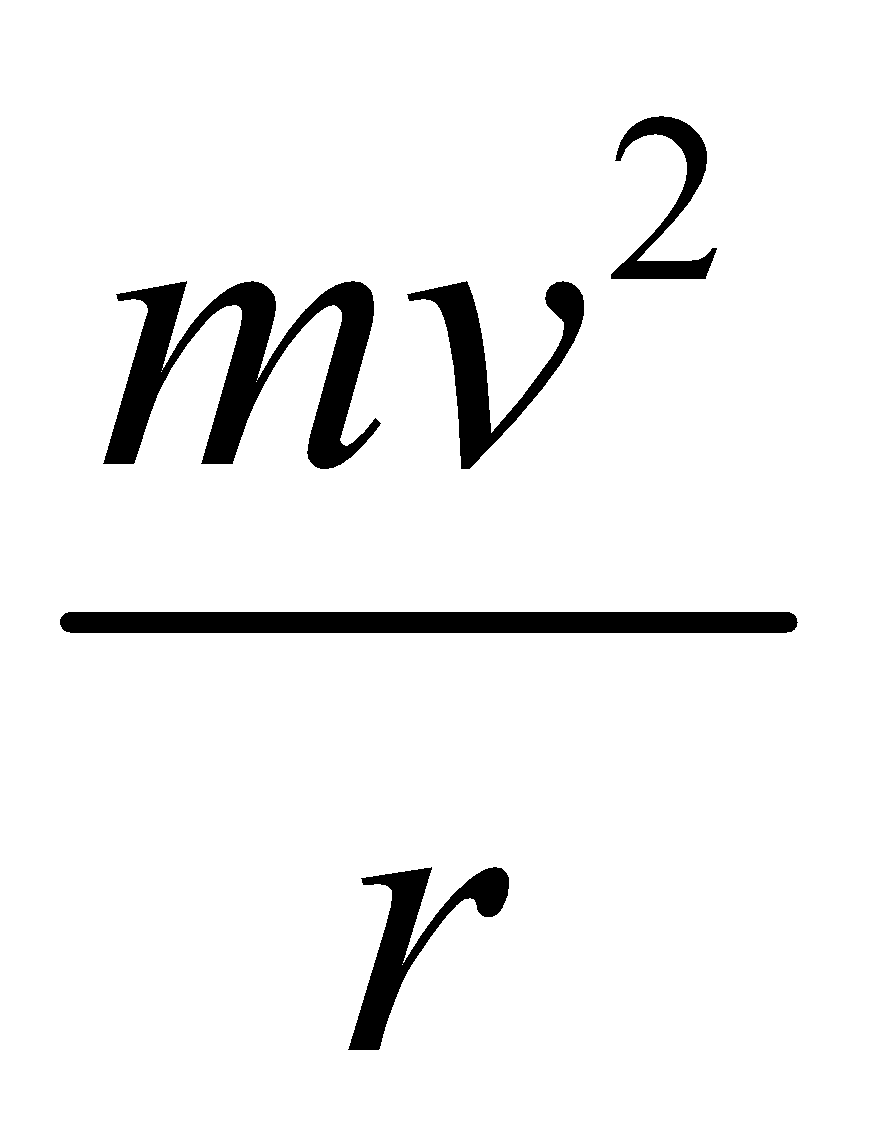
when v is max. and friction force will be acting down the slope.
Balancing the force horizontally, 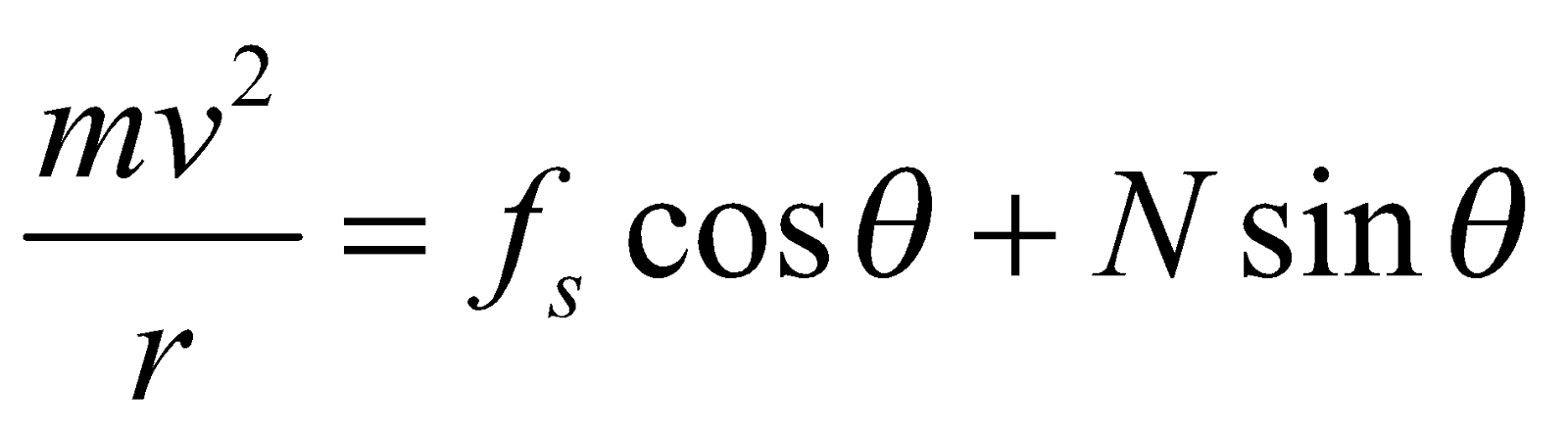 …(1)
…(1)
Balancing the force vertically, 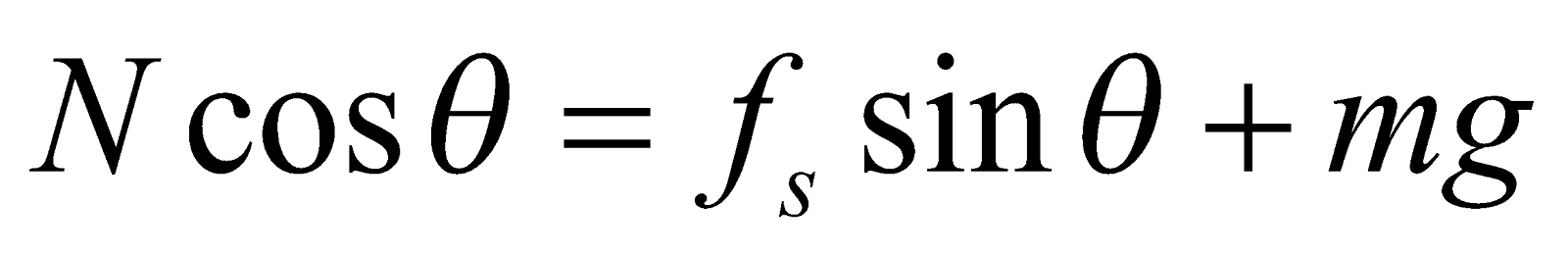 …(2)
…(2)
when v = maximum, f = fmax = fs = μN …(3)
From eqn. (2),
or 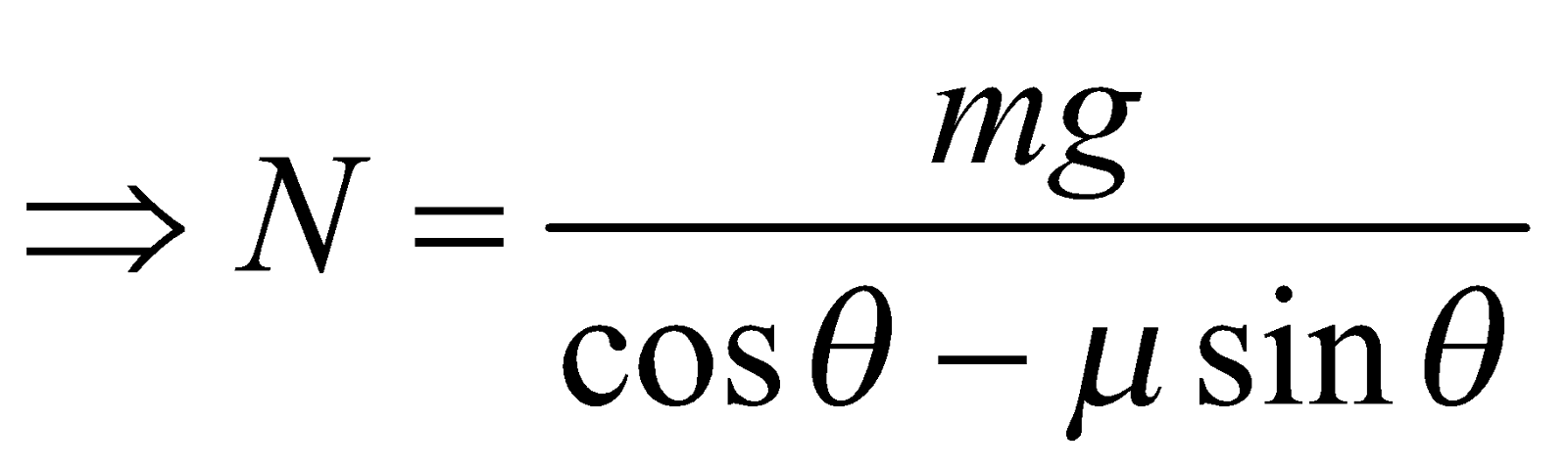
From eqns.(1) and (3),
Now in the case of minimum velocity with which body could move in a circular motion, the direction of friction will be opposite to that one in maximum velocity case.
and 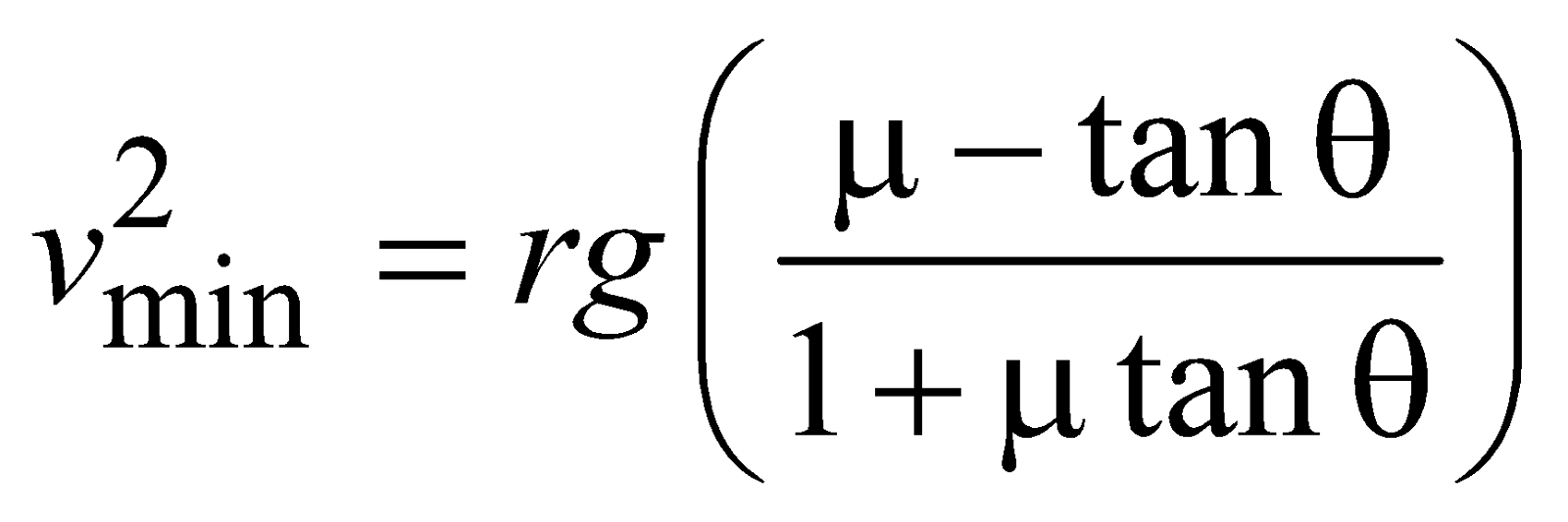
KEEP IN MEMORY
Whenever a particle is moving on the circular path then there must be some external force which will provide the necessary centripetal acceleration to the particle. For examples :
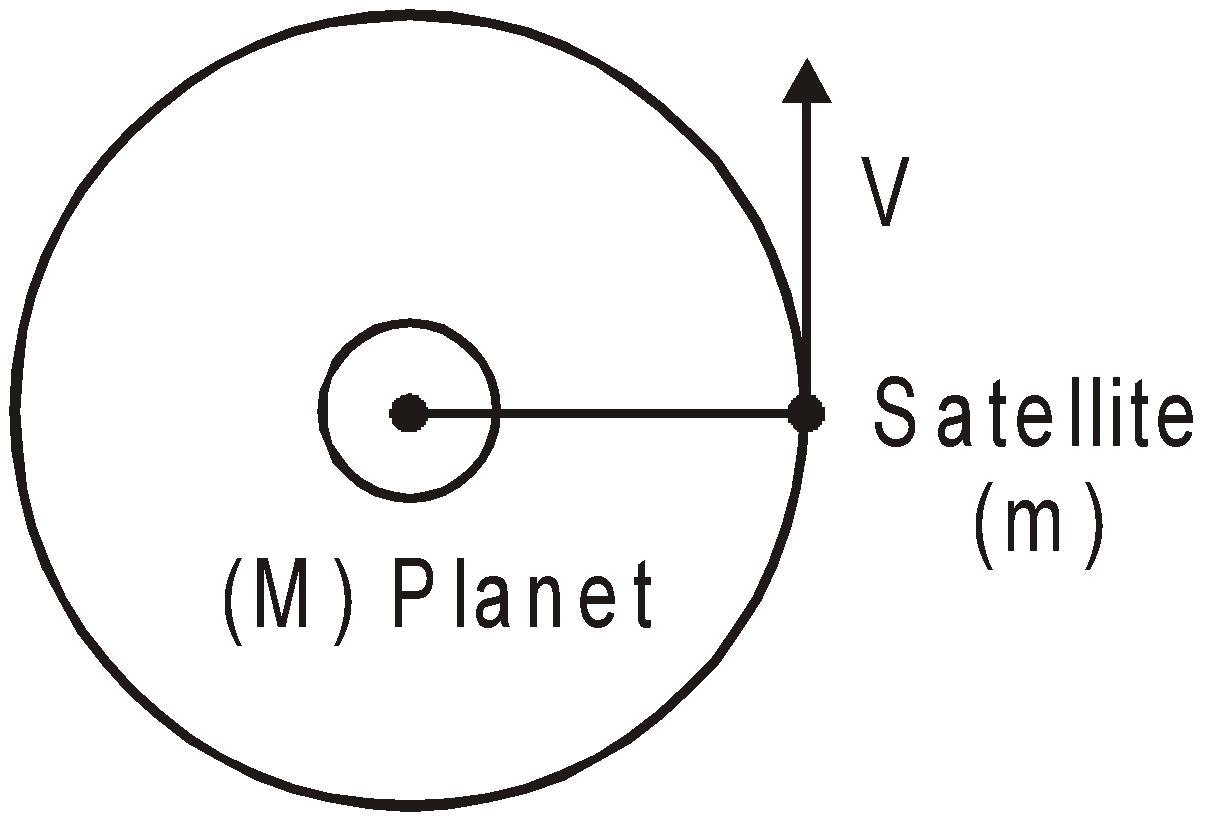
MOTION OF SATELLITE AROUND A PLANET
Here the centripetal force is provided by the gravitational force.
i.e. 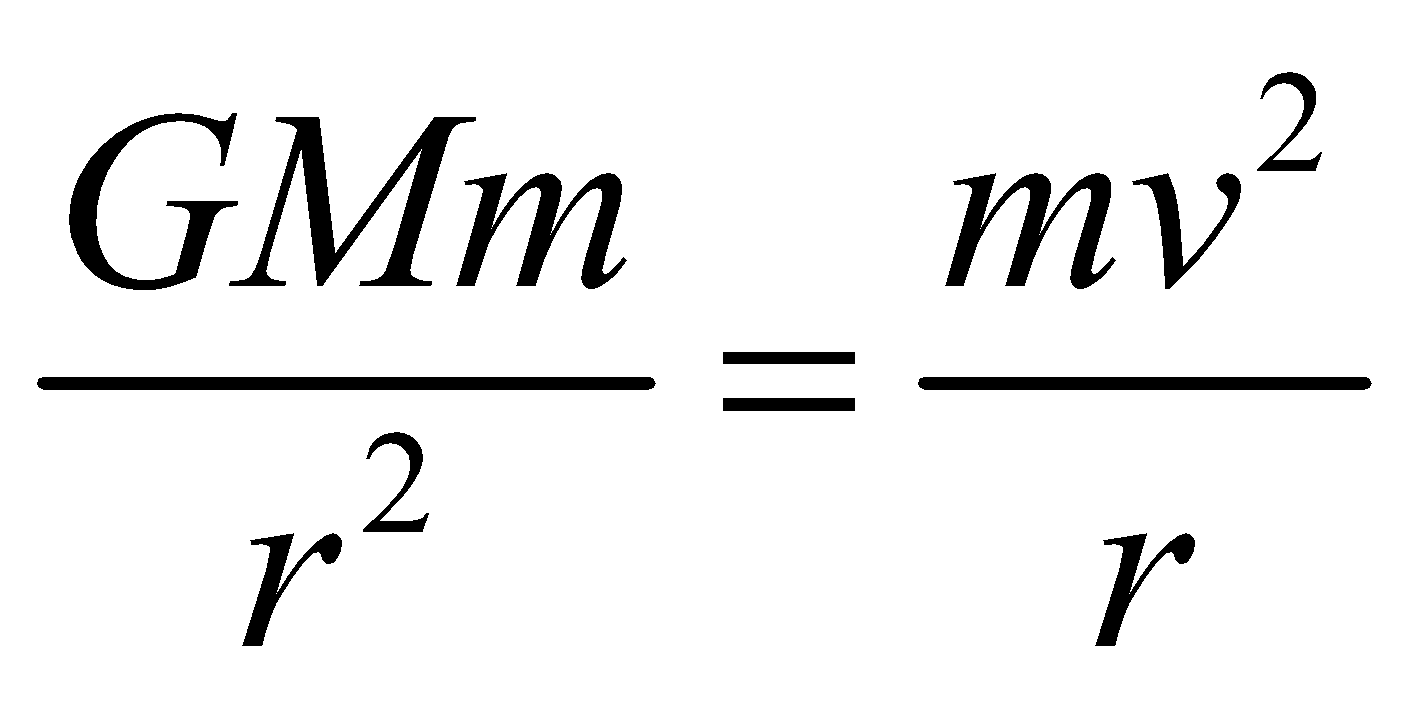
MOTION OF ELECTRON AROUND THE NUCLEUS
Here the required centripetal force is provided by the Coulombian force
i.e. 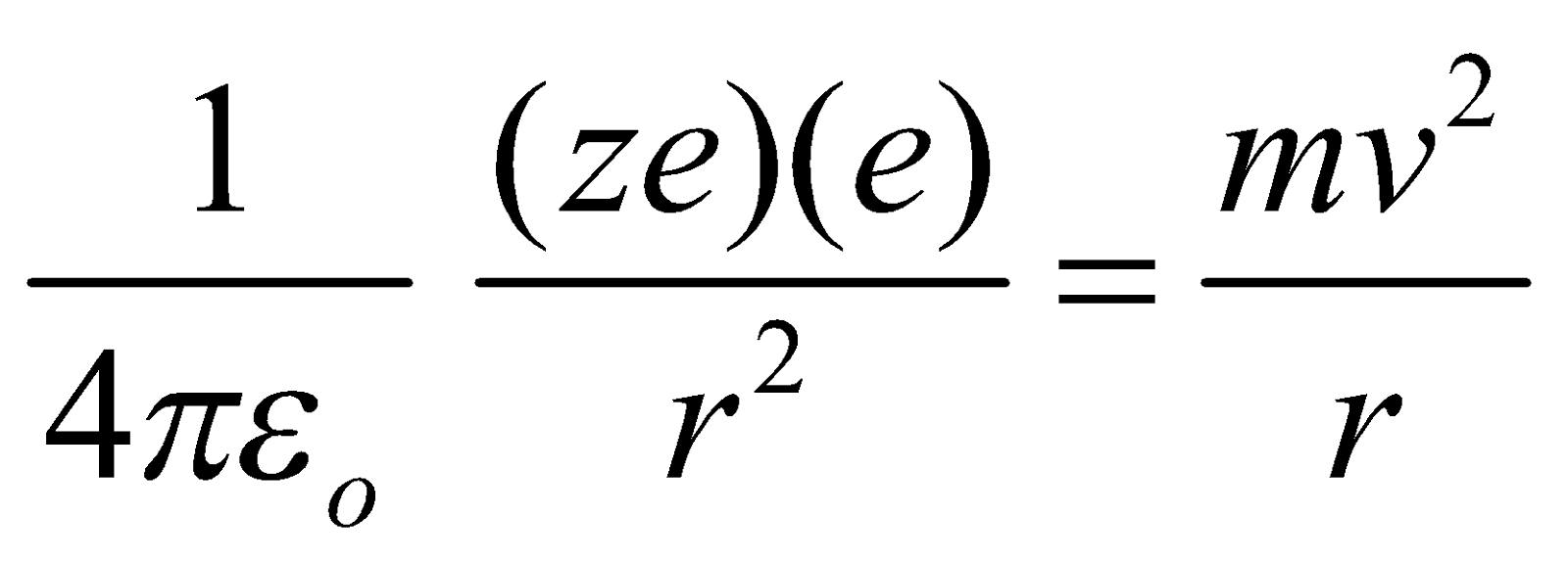
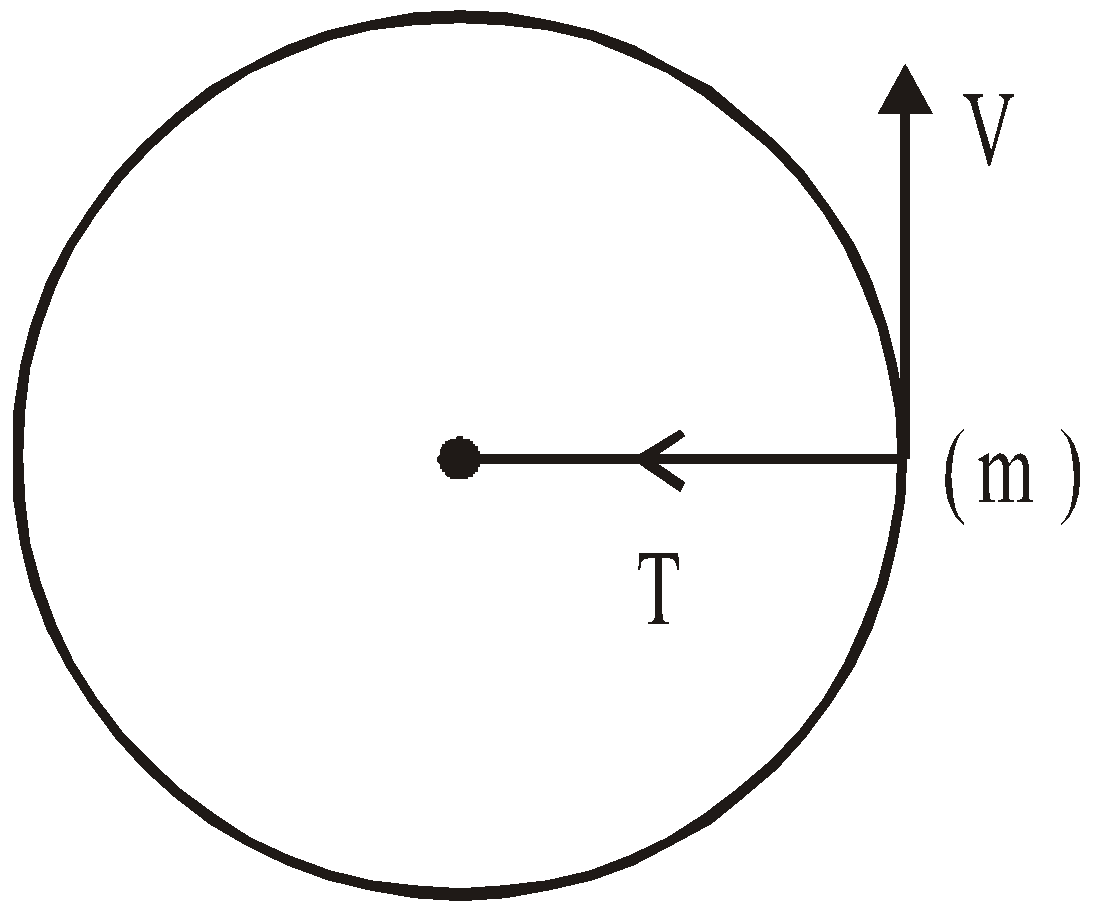
MOTION OF A BODY IN HORIZONTAL AND VERTICAL CIRCLE
Here the centripetal force is provided by the tension.
Horizontal circle
Vertical circle
At point A, 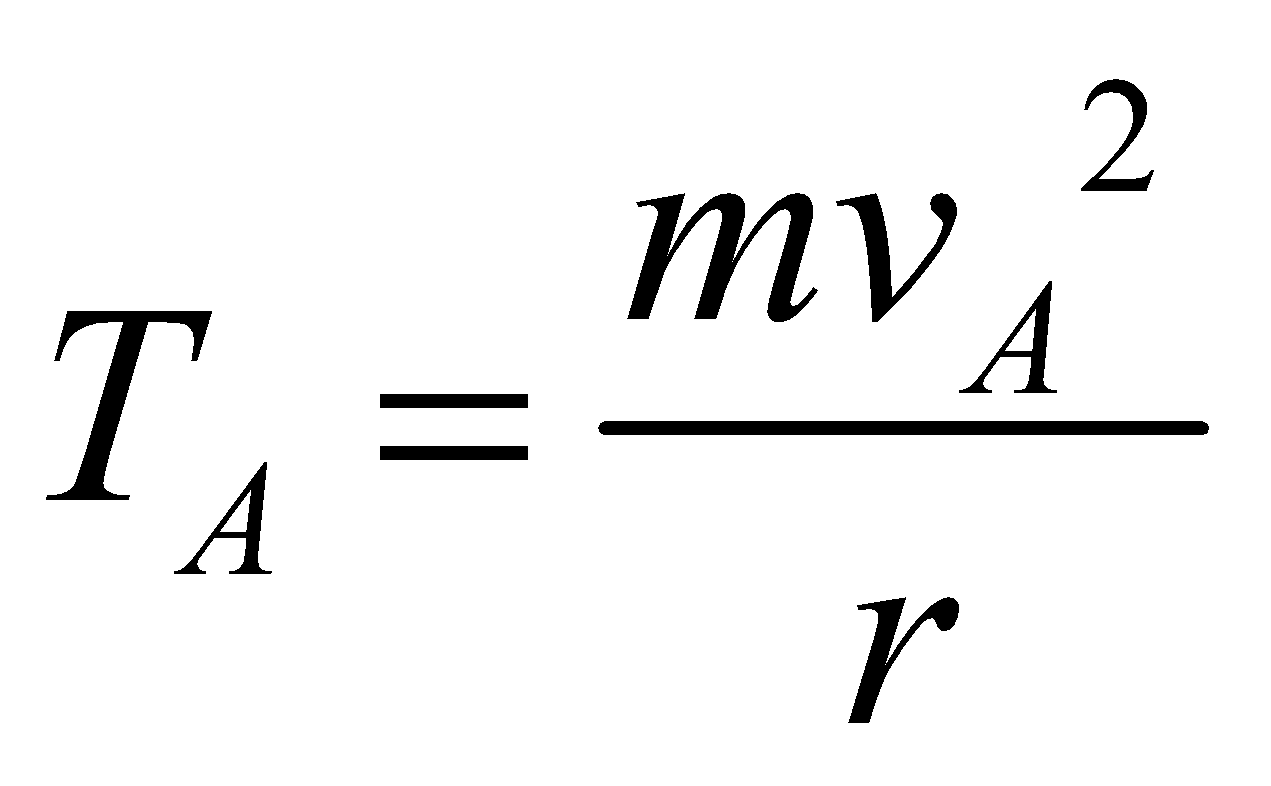
At point B, 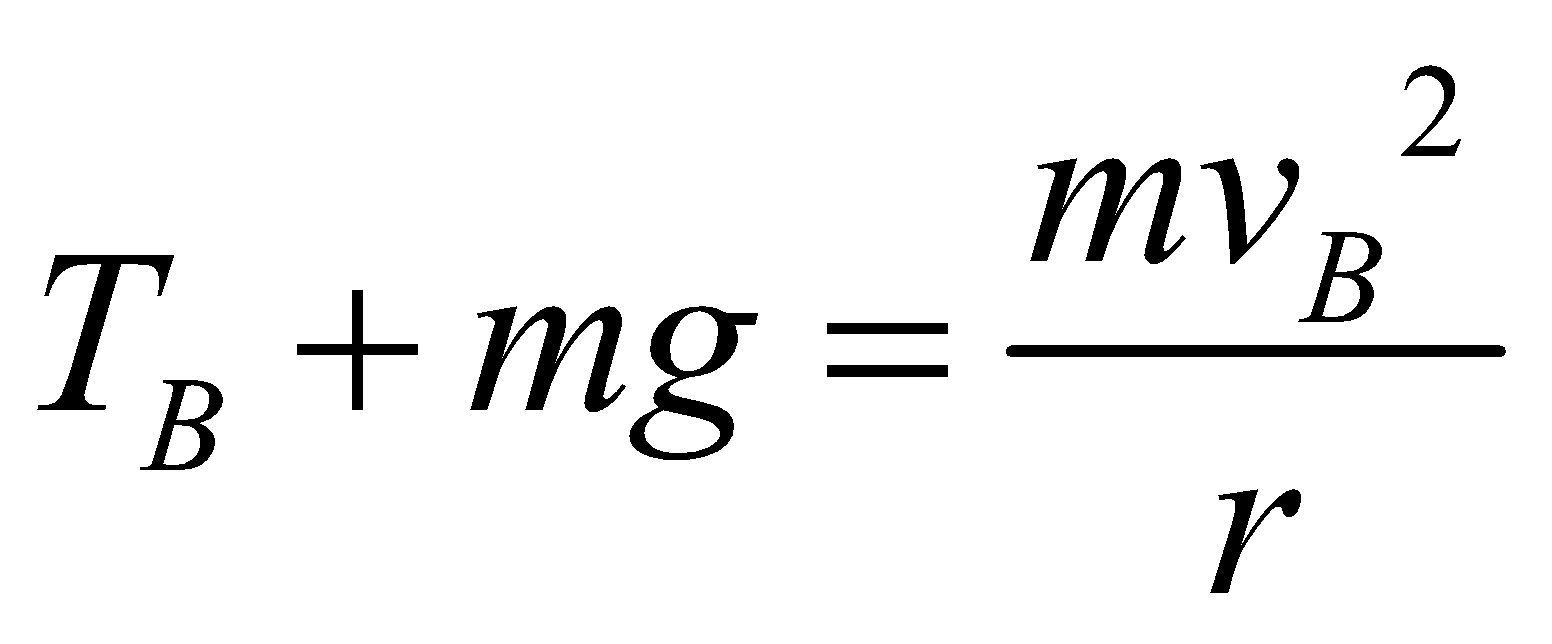
At point C, 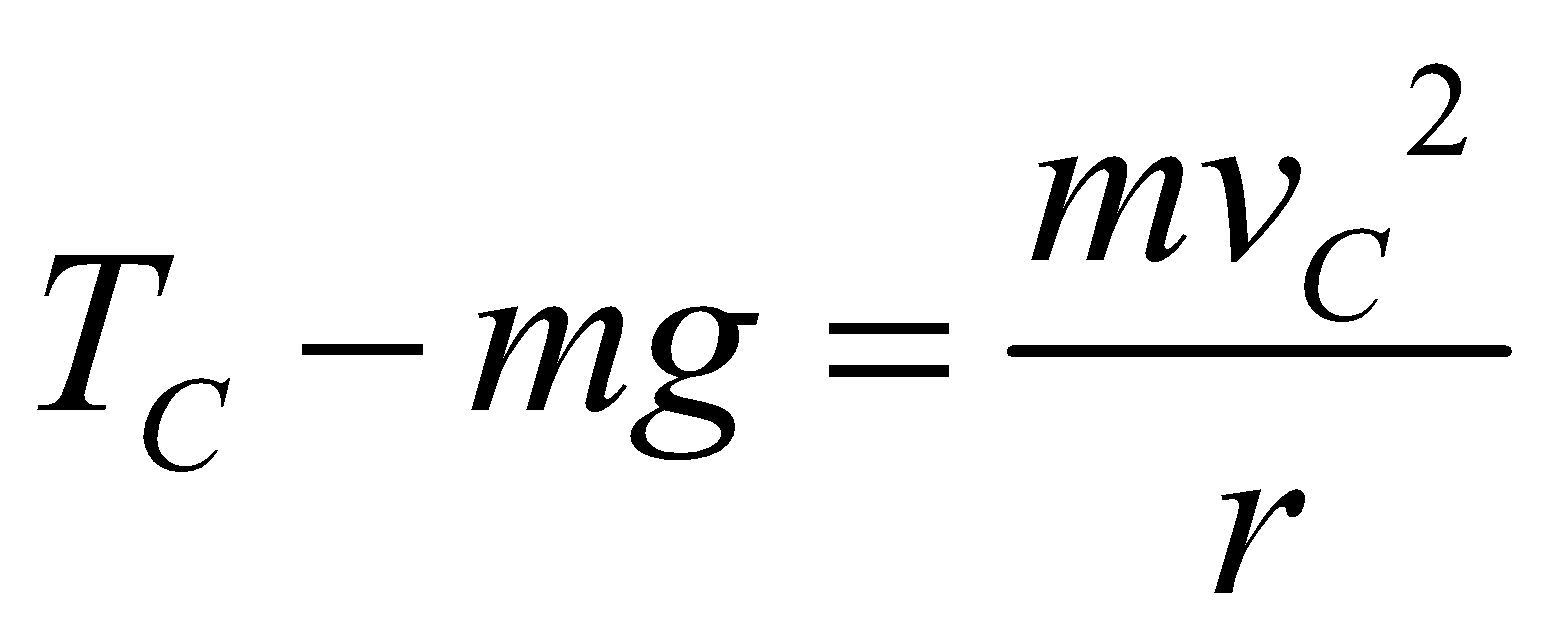
CONICAL PENDULUM
Consider an inextensible string of length l which is fixed at one end, A. At the other end is attached a particle P of mass m describing a circle with constant angular velocity ω in a horizontal plane.
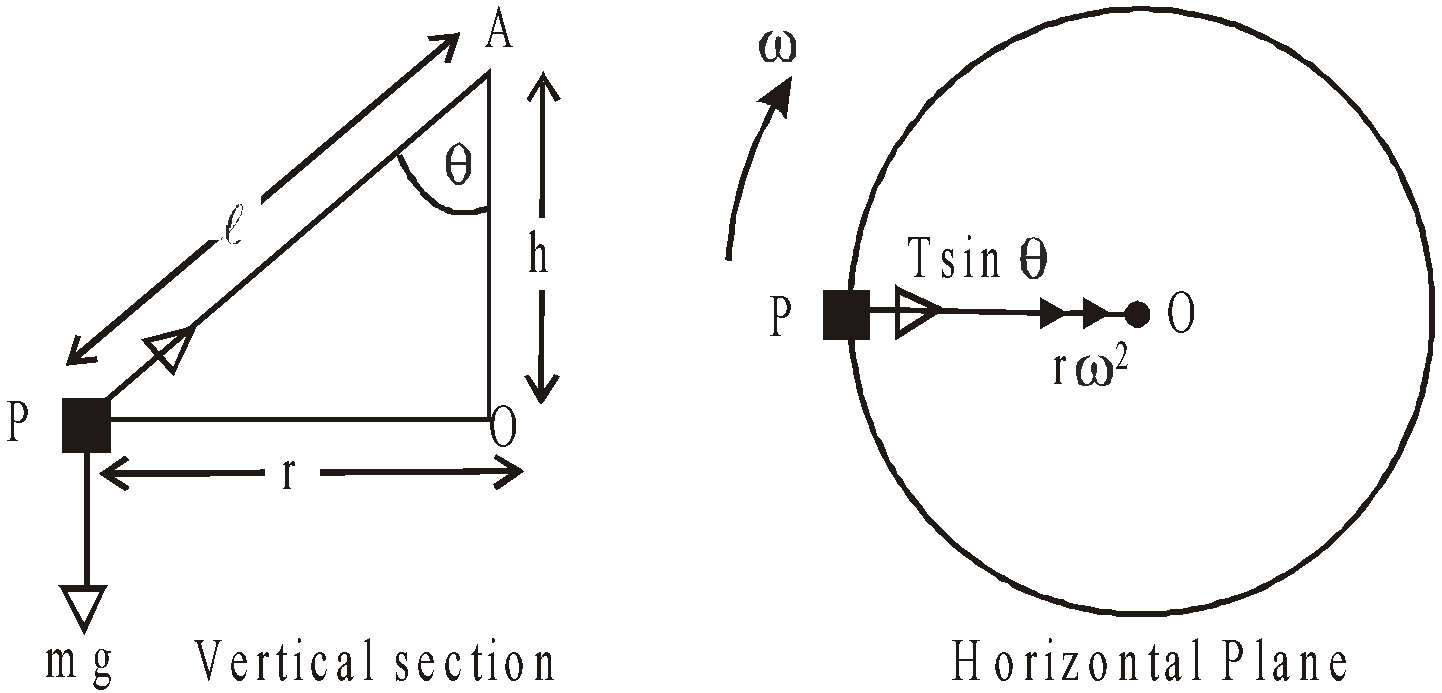
As P rotates, the string AP traces out the surface of a cone. Consequently the system is known as a conical pendulum.
Vertically, 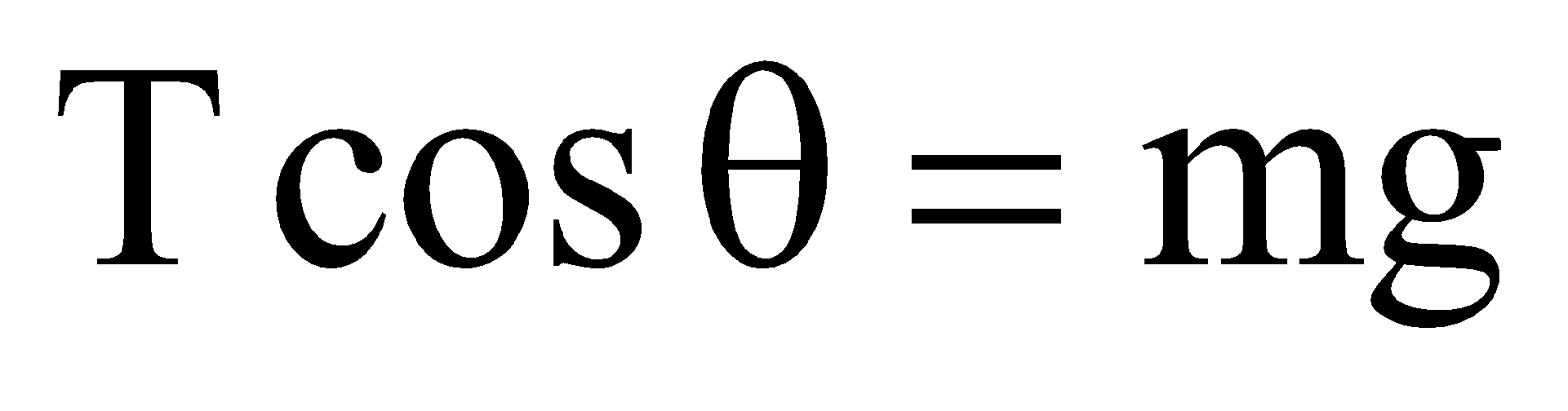 … (1)
… (1)
Horizontally, 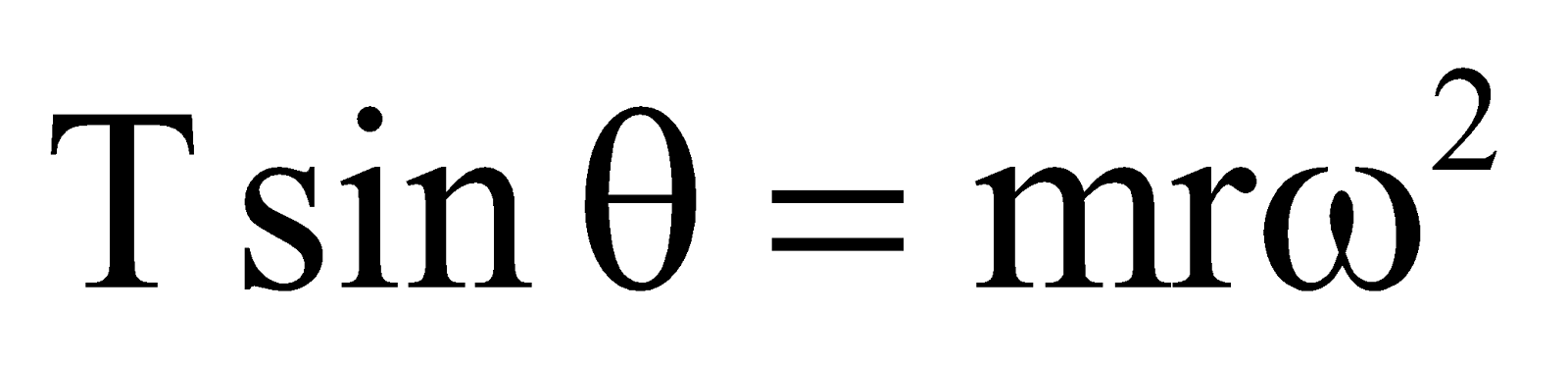 … (2)
… (2)
In triangle AOP, 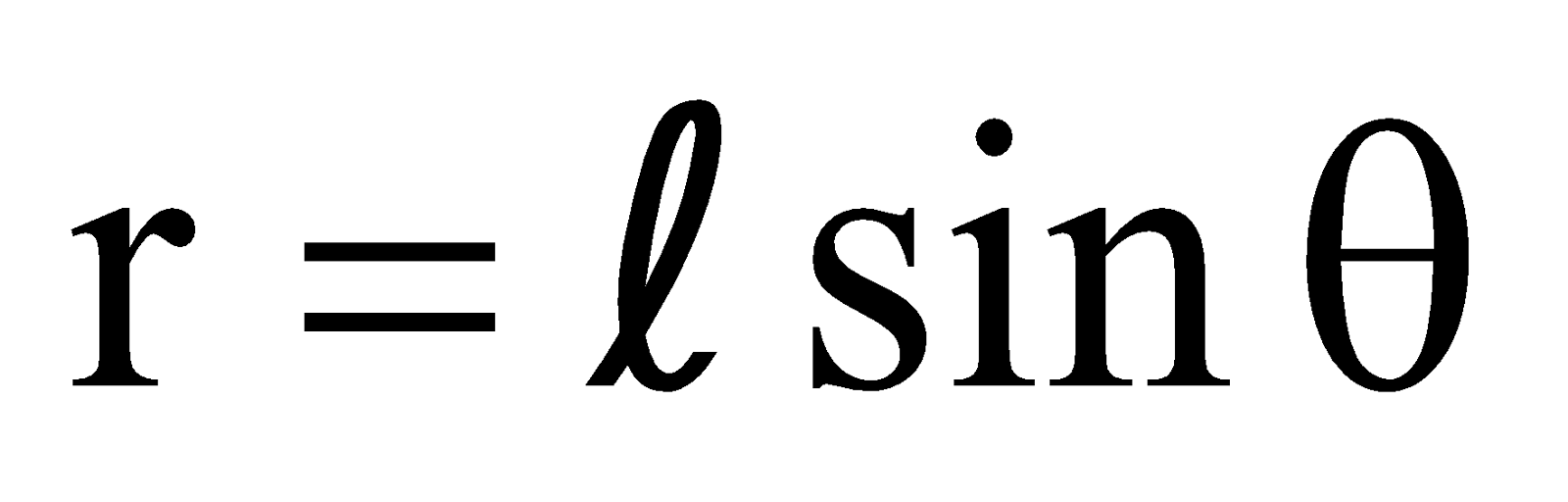 … (3)
… (3)
and 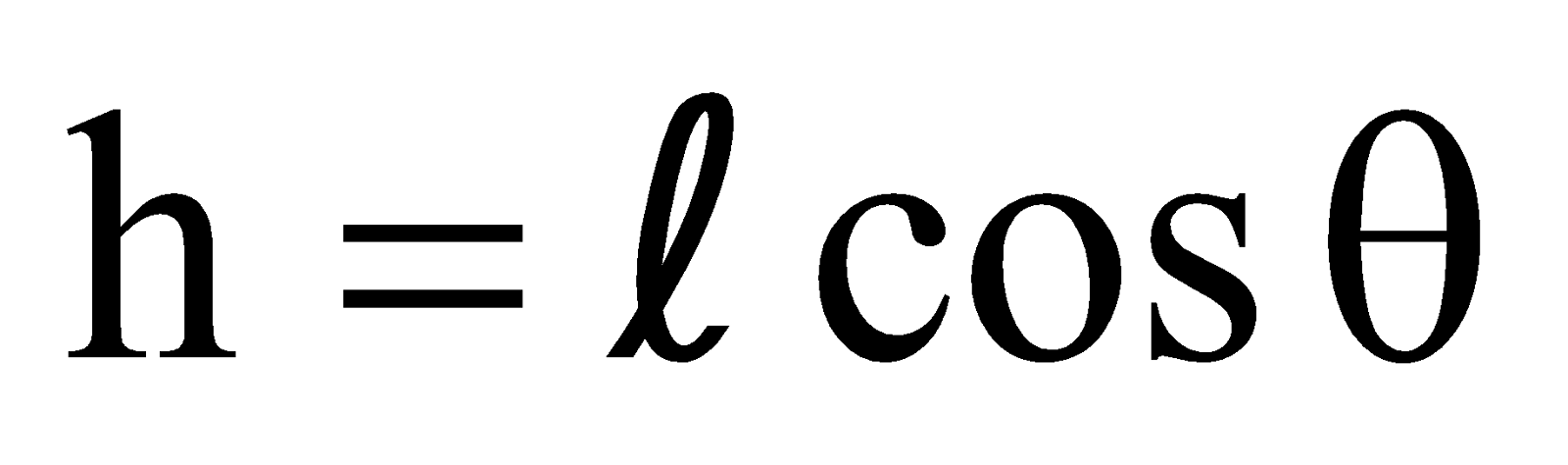 … (4)
… (4)
Several interesting facts can be deduced from these equations :
- It is impossible for the string to be horizontal.
This is seen from eqn.(1) in which 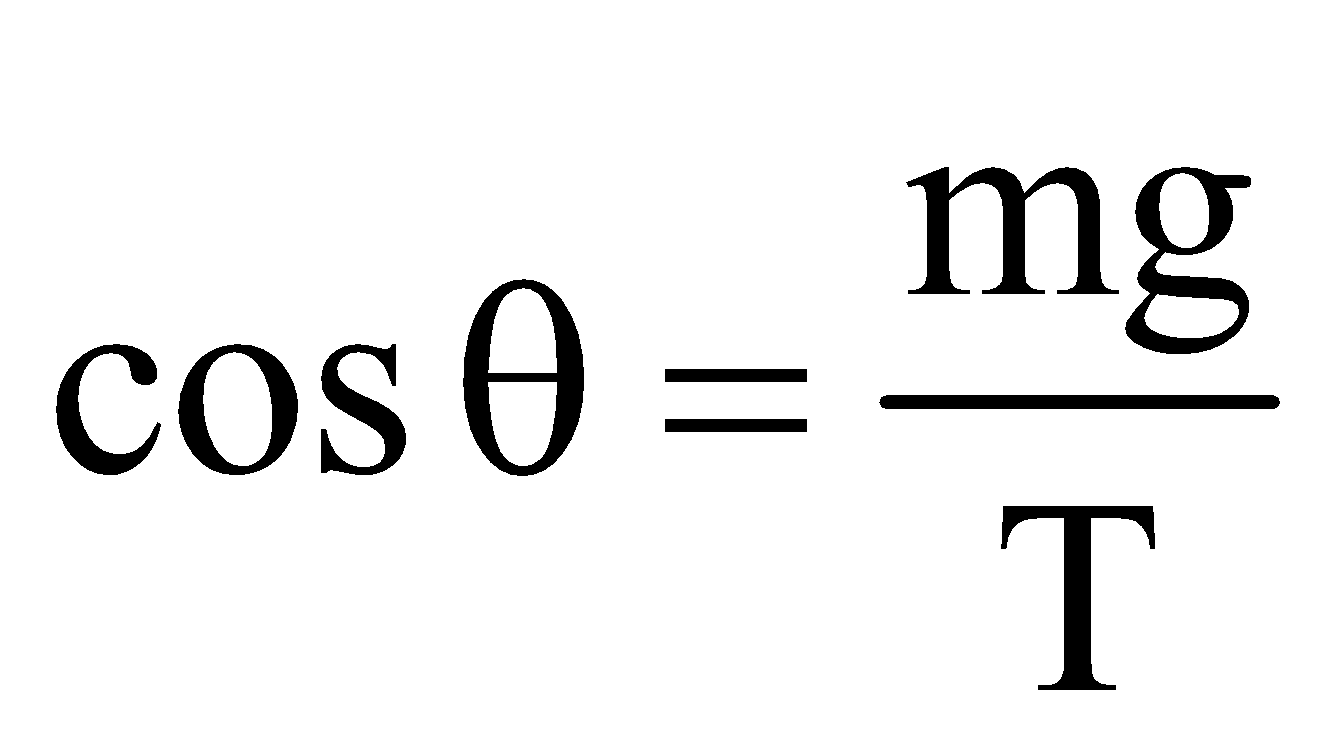 cannot be zero. Hence θ cannot be 90°.
cannot be zero. Hence θ cannot be 90°.
- The tension is always greater than mg.
This also follows from eqn. (1) as cos θ < 1 (θ is acute but not zero). Hence, T > mg
- The tension can be calculated without knowing the inclination of the string since, from eqn. (2) and (3)
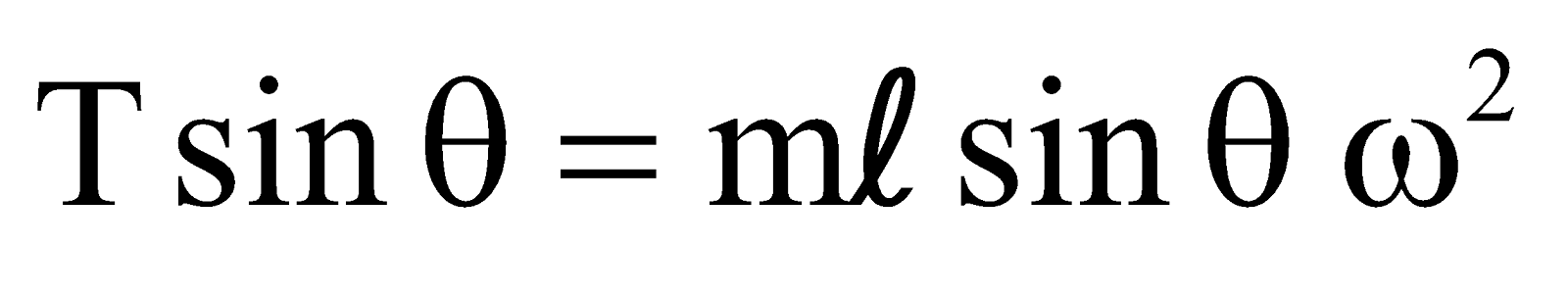 ⇒
⇒ 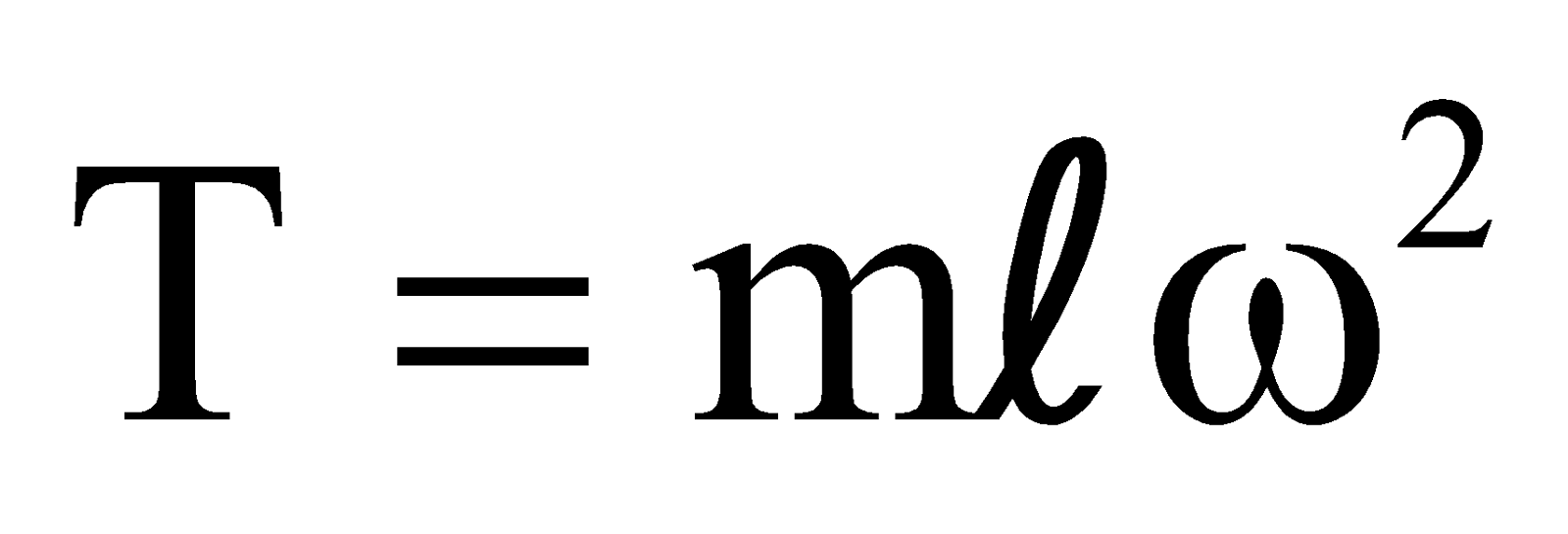
- The vertical depth h of P below A is independent of the length of the string since from eqn. (1) and (4)
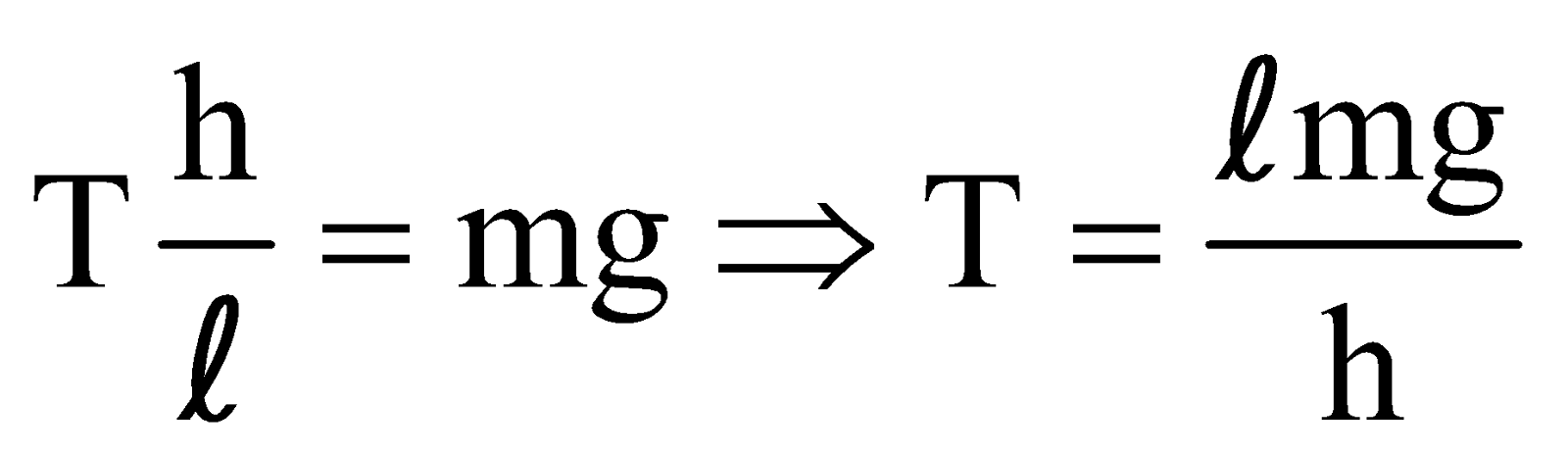 but
but 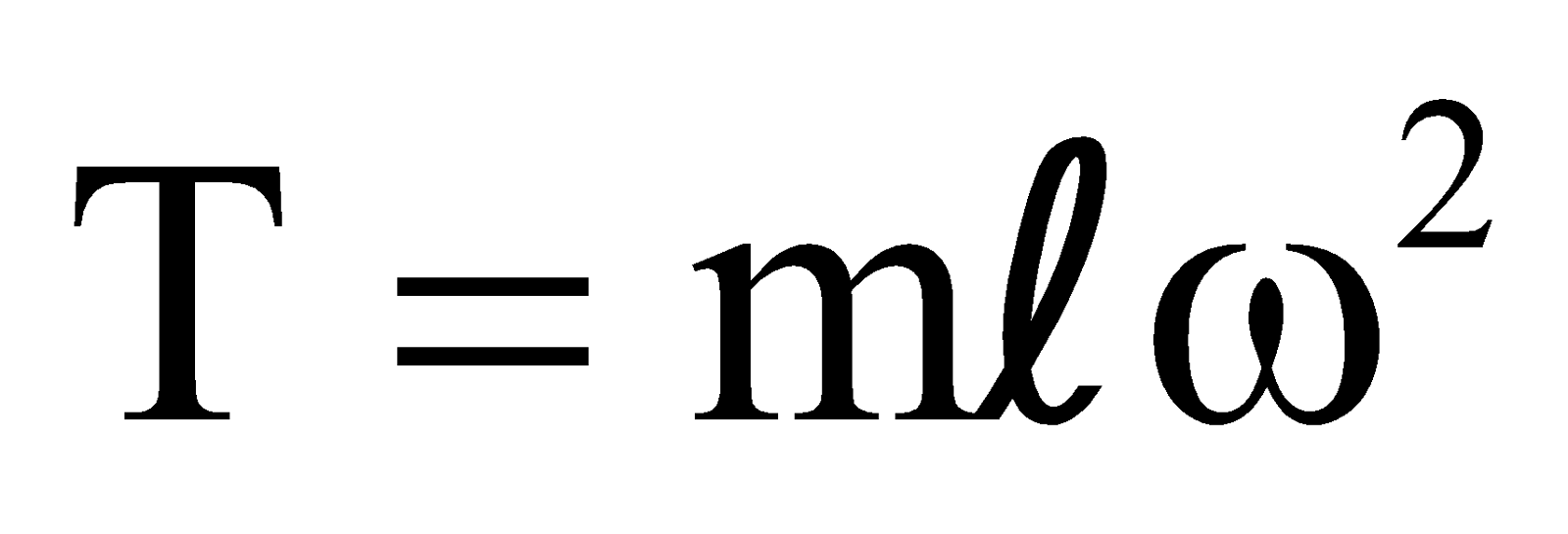
Therefore 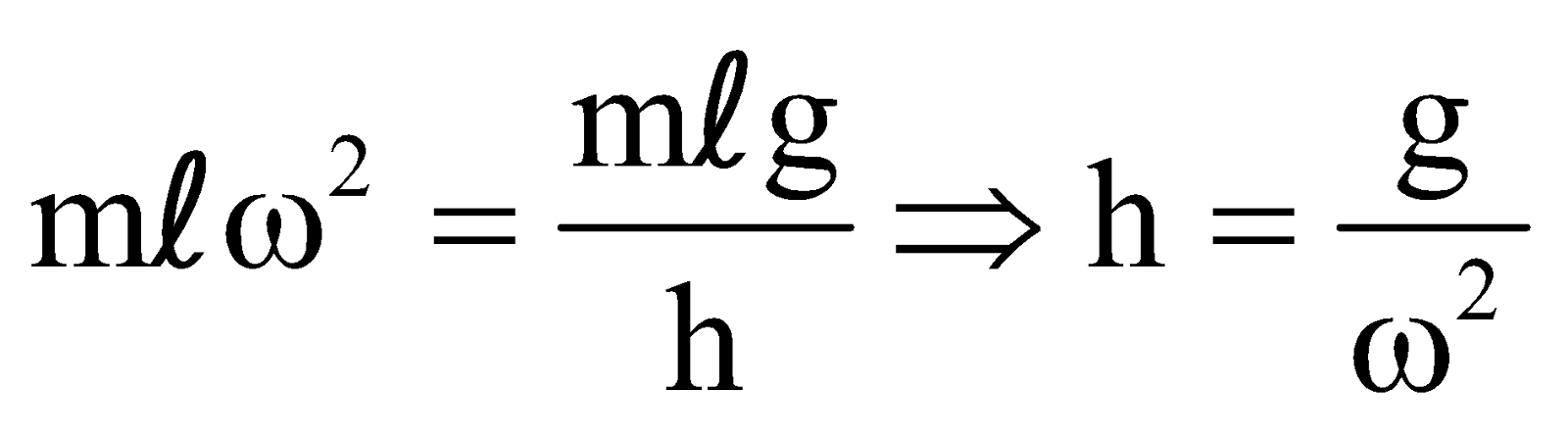
which is independent of l.