3.2 Modelling a gas
Essential Idea:
The properties of ideal gases allow scientists to make predictions of the behaviour of real gases
Understandings:
- Pressure
- Equation of state for an ideal gas
- Kinetic model of an ideal gas
- Mole, molar mass and the Avogadro constant
- Differences between real and ideal gases
Applications and Skills:
- Solving problems using the equation of state for an ideal gas and gas laws
- Sketching and interpreting changes of state of an ideal gas on pressure– volume, pressure–temperature and volume–temperature diagrams
- Investigating at least one gas law experimentally
Data booklet reference:
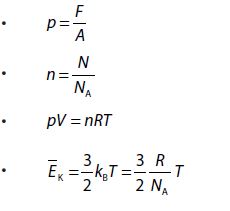
KINETIC THEORY OF GASES
BEHAVIOUR OF GASES
IDEAL GAS
\(P\propto \frac{1}{V}\) When T is constant
- At constant temperature and pressure, the rms speed of diffusion of two gases is inversely proportional to the square root of the relative density
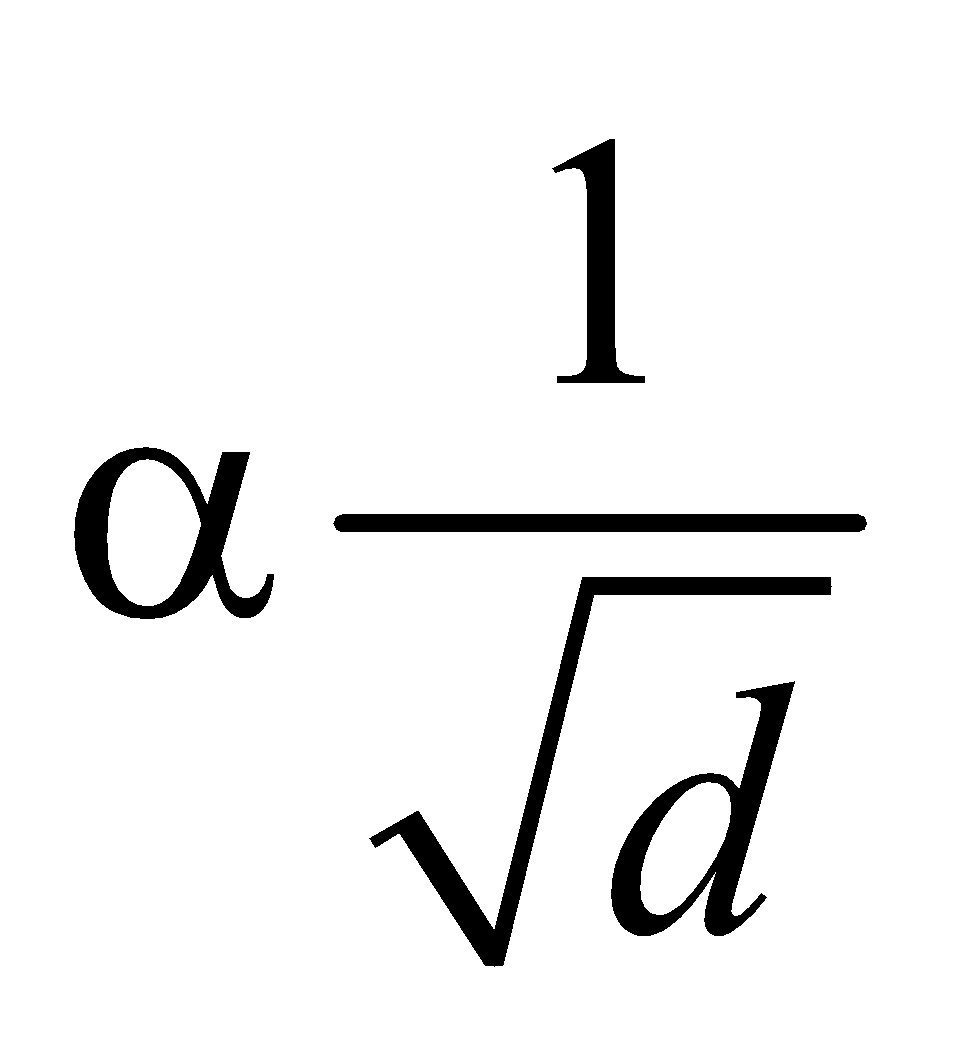 ⇒
⇒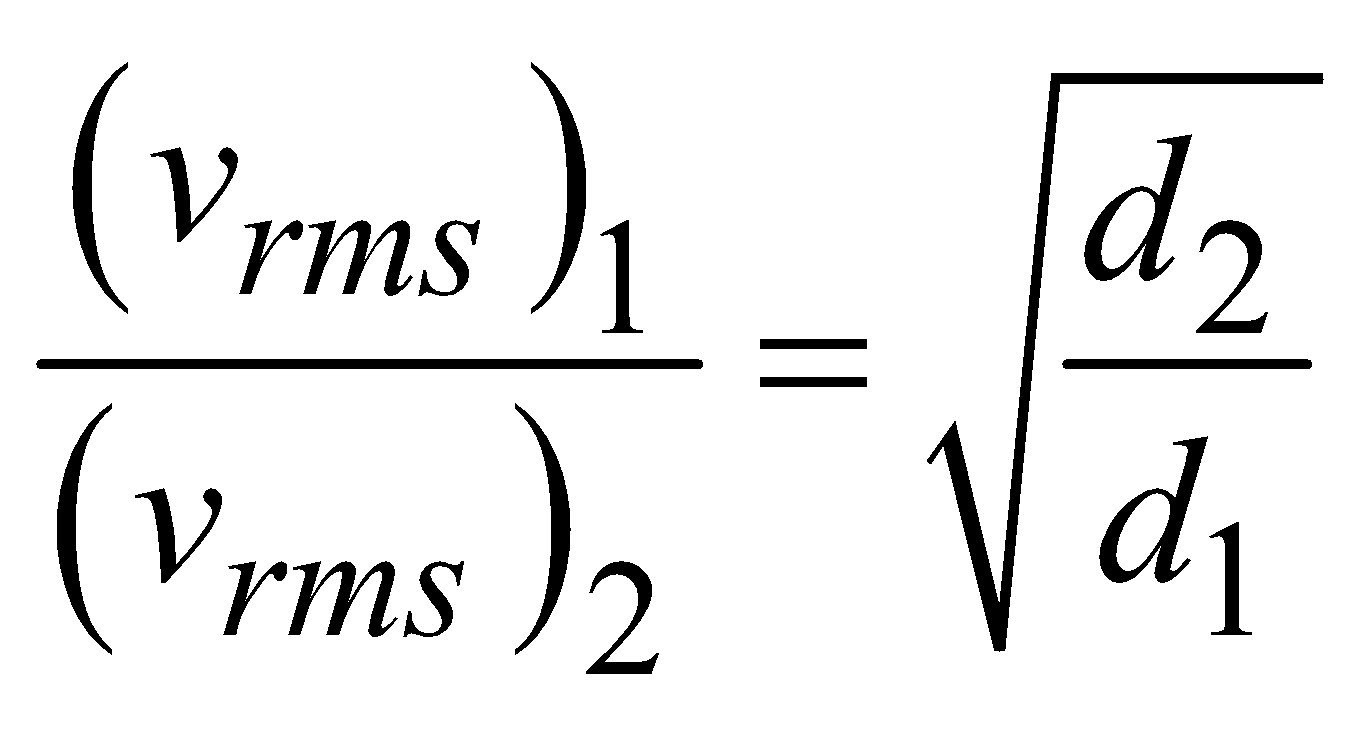
- According to Graham’s law, the rate of diffusion of a gas is inversely proportional to the square root of its density, provided pressure and temperature are constant

R = 8.31 J/mol K and R = NAk, where k is Boltzmann’s constant (NA is Avogadro number). n is the number of moles of a gas and
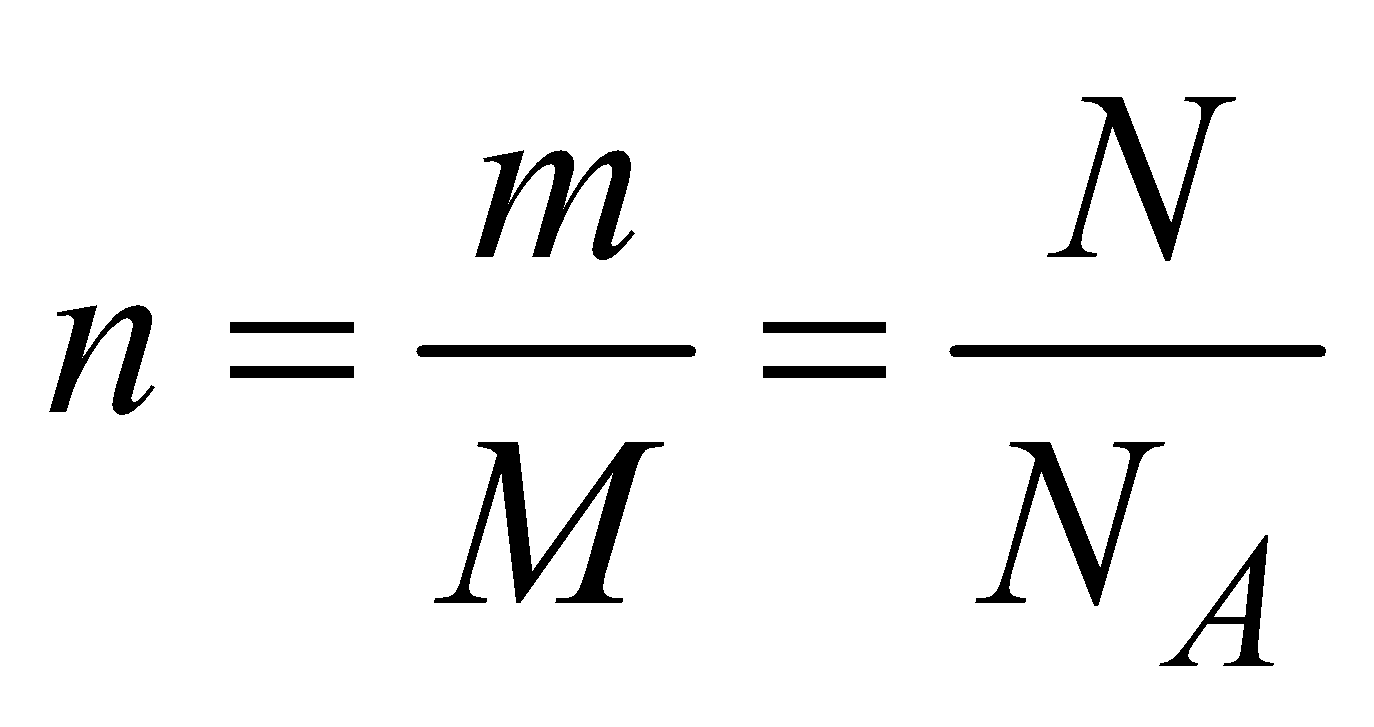 , NA is Avogadro’s number
, NA is Avogadro’s number EQUATION OF REAL GAS
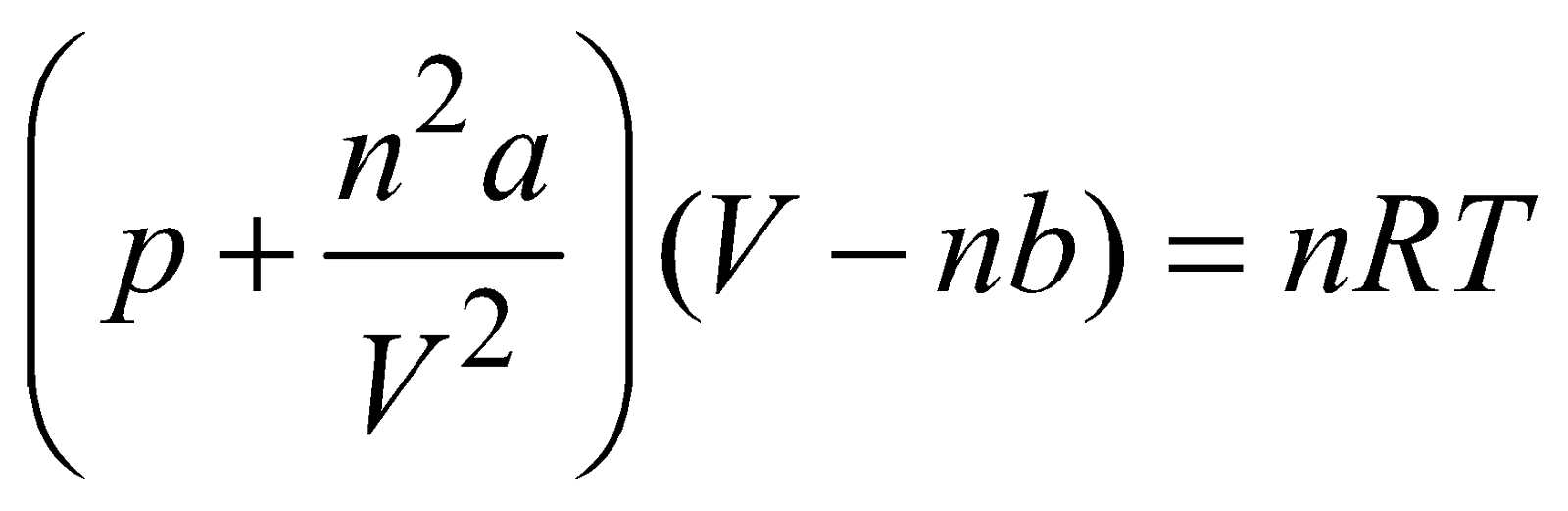
CRITICAL TEMPERATURE, VOLUME AND PRESSURE
- The temperature at or below which a gas can be liquefied by applying pressure alone is called critical temperature TC. It is given by
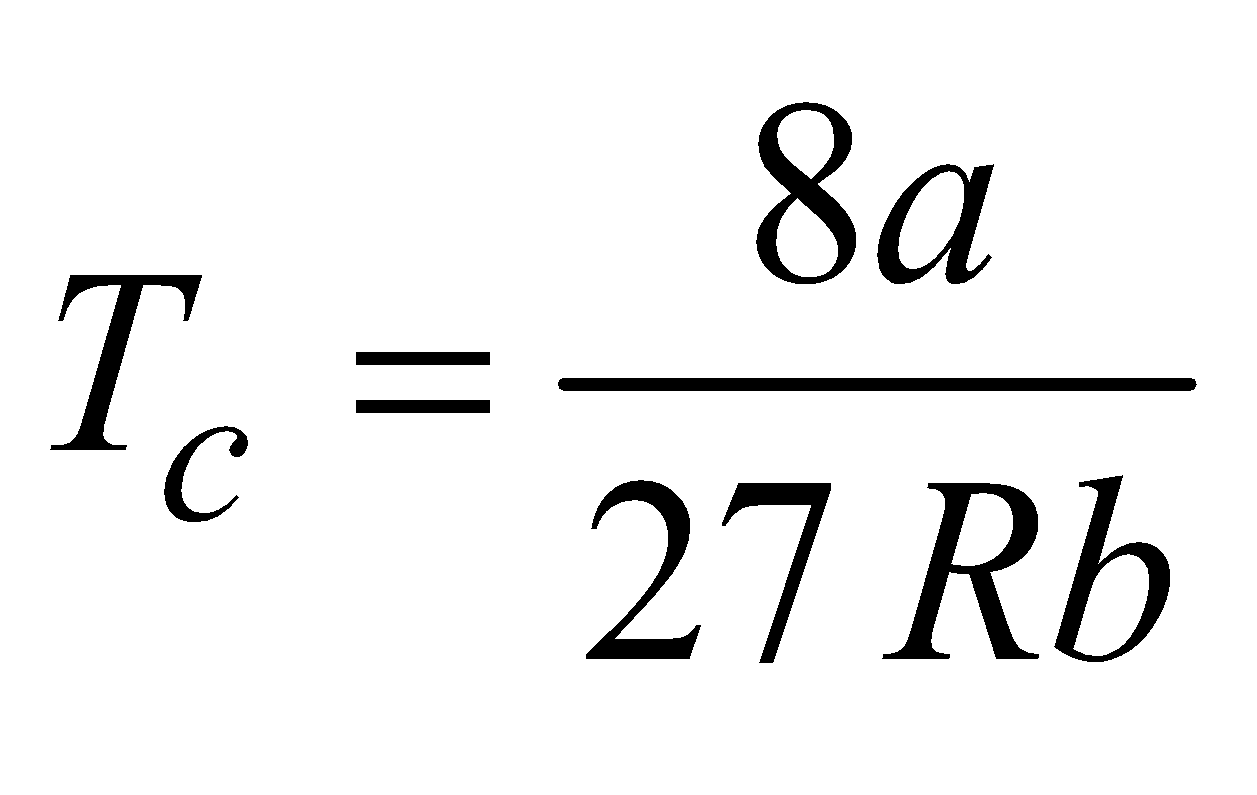
- The volume of gas at a critical temperature TC is called critical volume VC, where VC = 3b
- The pressure of gas at a critical temperature TC is called critical pressure PC, where
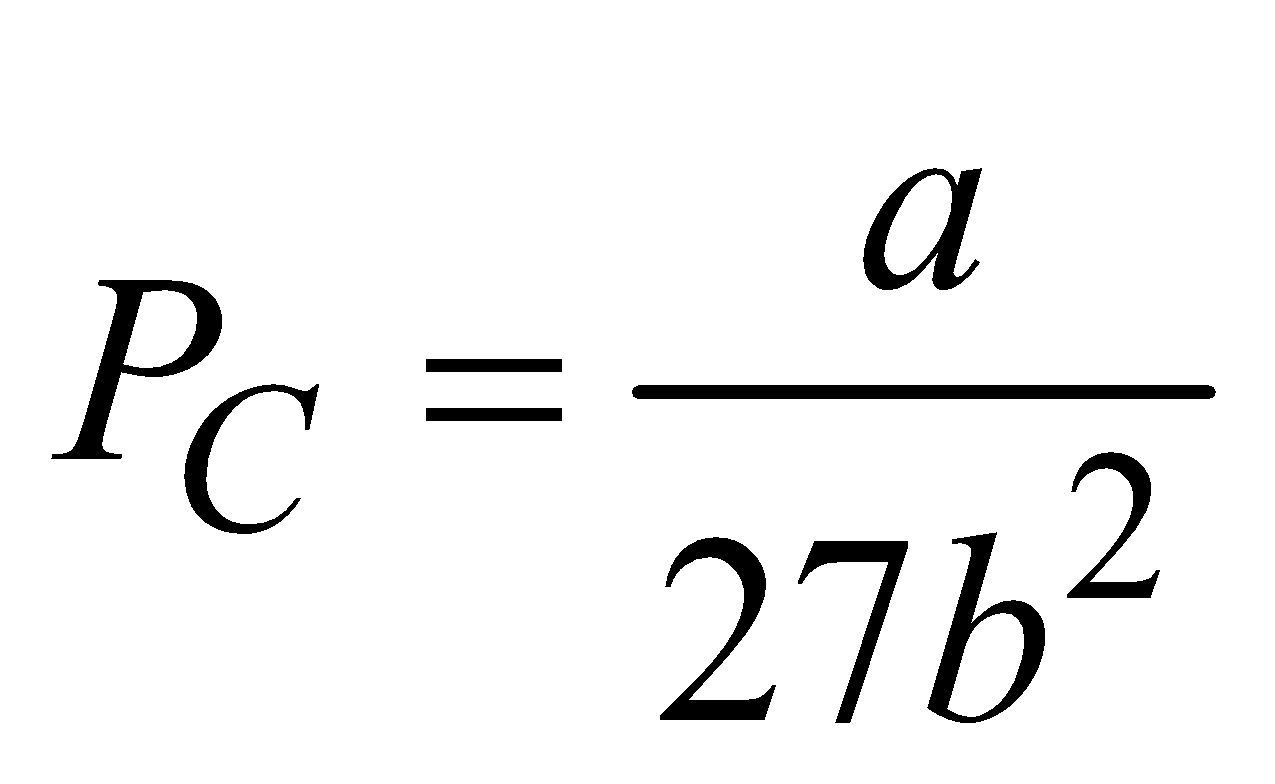
GAS EQUATION
- The gases found in nature are real gases.
- The real gas do not obey ideal gas equation but they obey Vander Waal’s gas equation
- a’ depends upon the intermolecular force and the nature of gas.
- b’ depends upon the size of the gas molecules and represents the volume occupied by the molecules of the gas.
- The molecules of real gas have potential energy as well as kinetic energy.
- The real gas can be liquefied and solidified.
- The real gases like CO2, NH3, SO2 etc. obey Vander Wall’s equn at high pressure and low temperature.
KINETIC THEORY OF AN IDEAL GAS
- A gas consist of particles called molecules which move randomly in all directions.
- The volume of molecule is very small in comparison to the volume occupied by gas i.e., the size of molecule is infinitesimally small.
- The collision between two molecules or between a molecule and wall are perfectly elastic and collision time (duration of collision) is very small.
- The molecules exert no force on each other or on the walls of containers except during collision.
- The total number of molecules are large and they obey Newtonian mechanics.
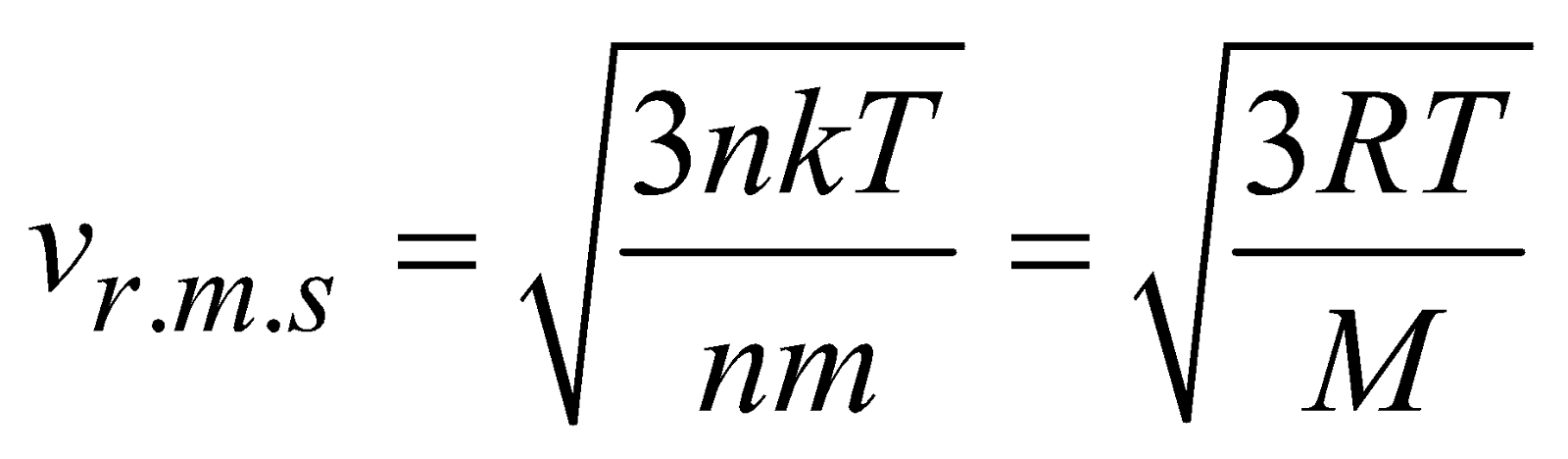
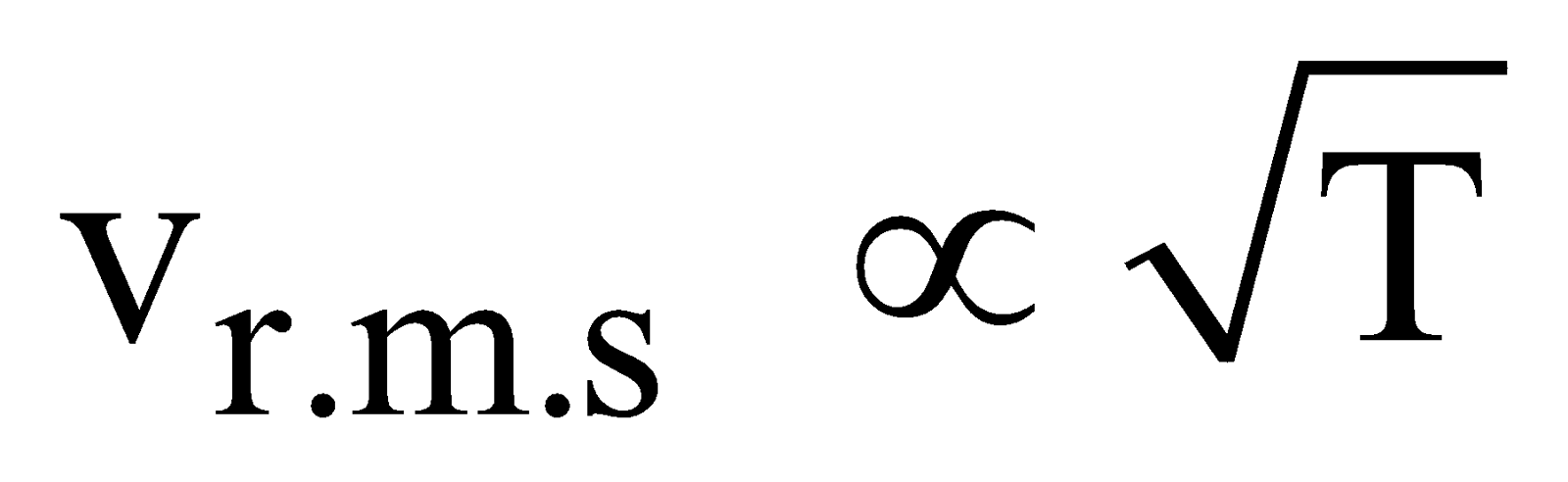
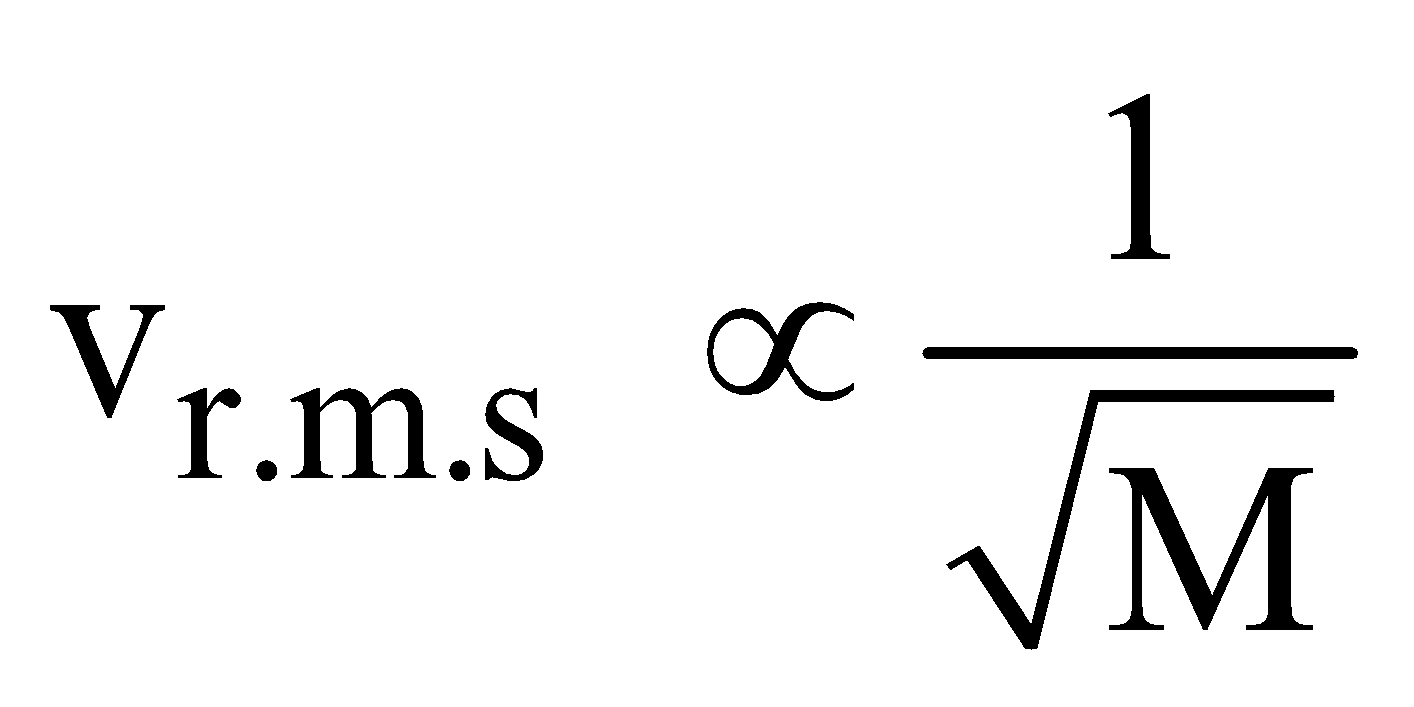 , where M is molecular mass of the gas.
, where M is molecular mass of the gas.
The kinetic molecular theory can be used to explain each of the experimentally determined gas laws.
DEGREE OF FREEDOM
3 degree of freedom, all translational.
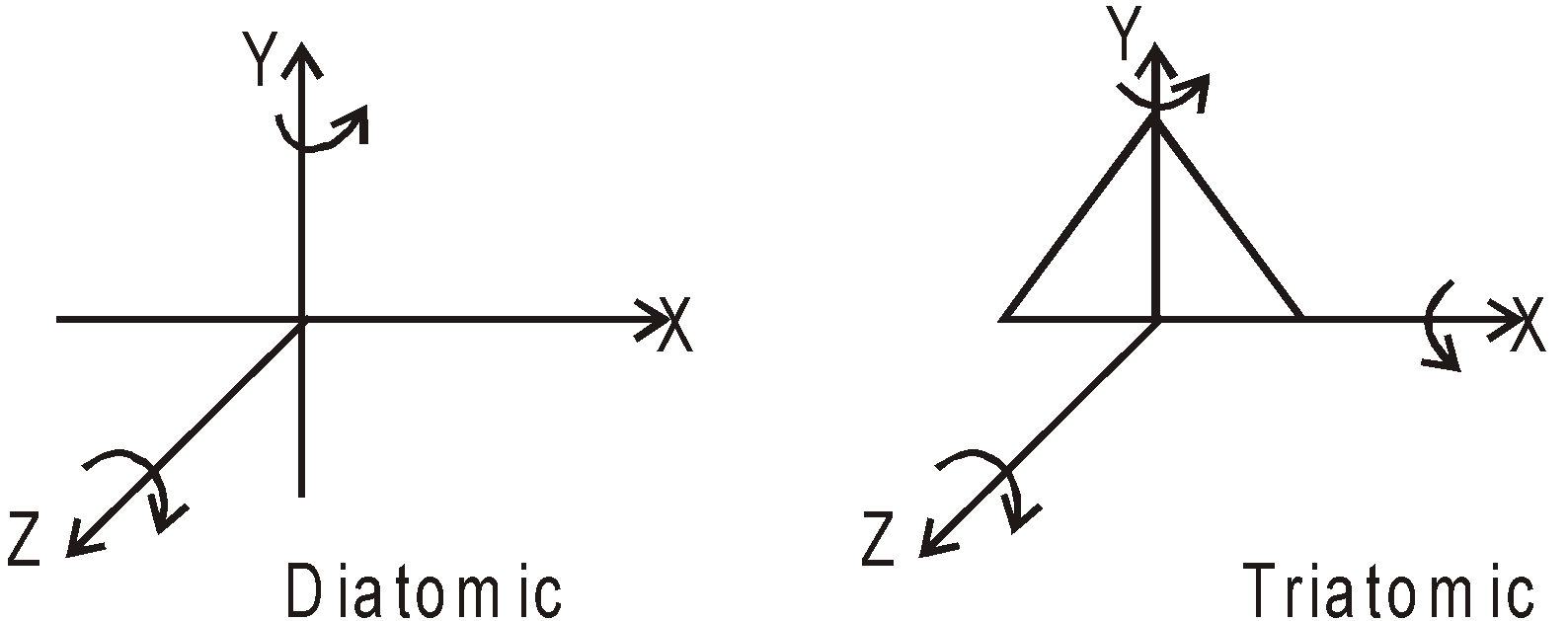
MEAN FREE PATH
LAW OF EQUIPARTITION OF ENERGY
- Real gases behave like perfect gas at high temperature and low pressure.
- Real gases deviate most from the perfect gas at high pressure and low temperature.
- Gaseous state of matter below critical temperature is called vapours. Below critical temperature gas is vapour and above critical temperature vapour is gas.
- Random motion of the constituents of the system involving exchange of energy due to mutual collisions is called thermal motion.
- Total kinetic energy or internal energy or total energy does not depend on the direction of flow of heat. It is determined by the temperature alone.
- The internal energy of a perfect gas consists only of kinetic energy of the molecules. But in case of the real gas it consists of both the kinetic energy and potential energy of inter molecular configuration.
DISTRIBUTION OF MOLECULAR SPEEDS
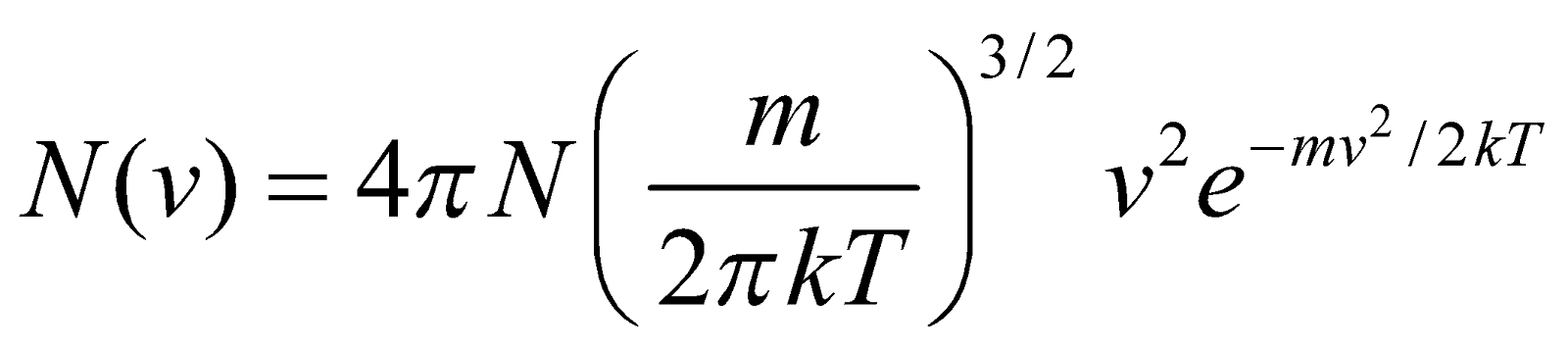 …(1)
…(1)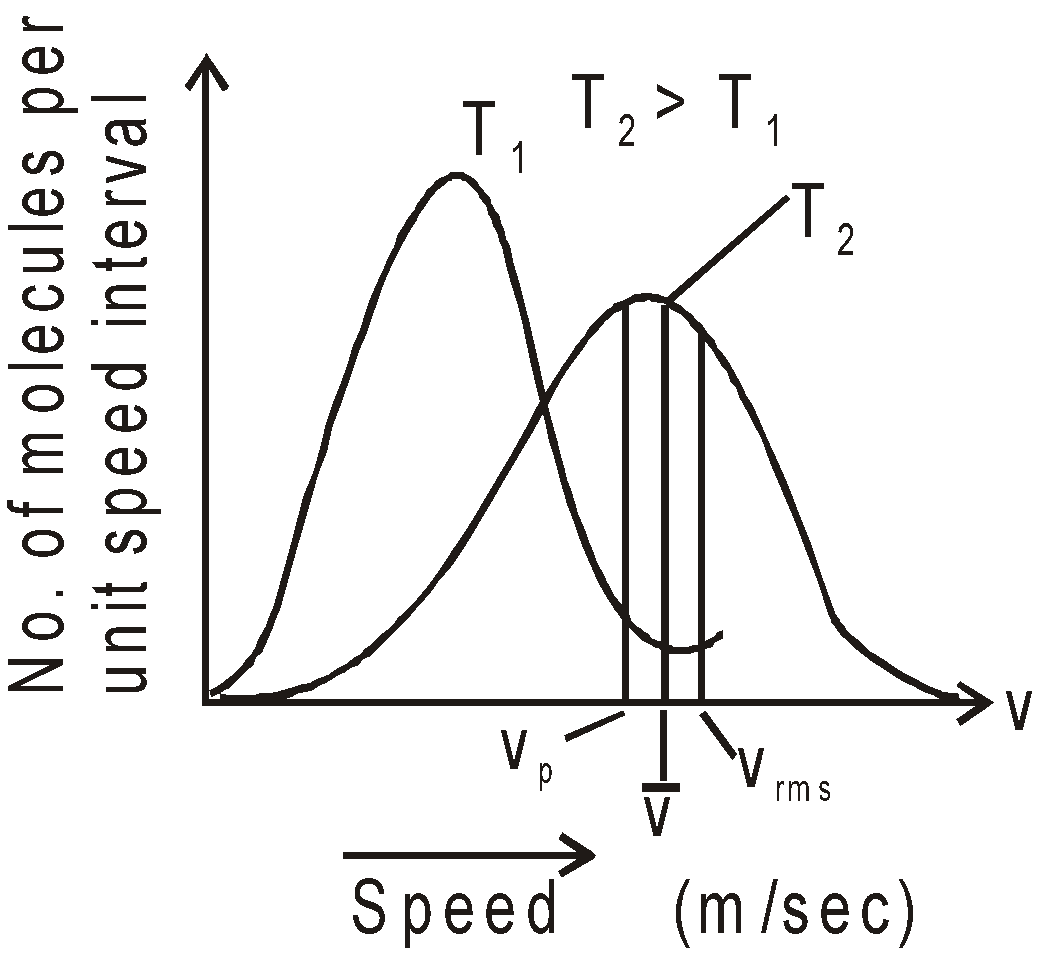
AVERAGE, ROOT MEAN SQUARE AND MOST PROBABLE SPEED
AVERAGE SPEED
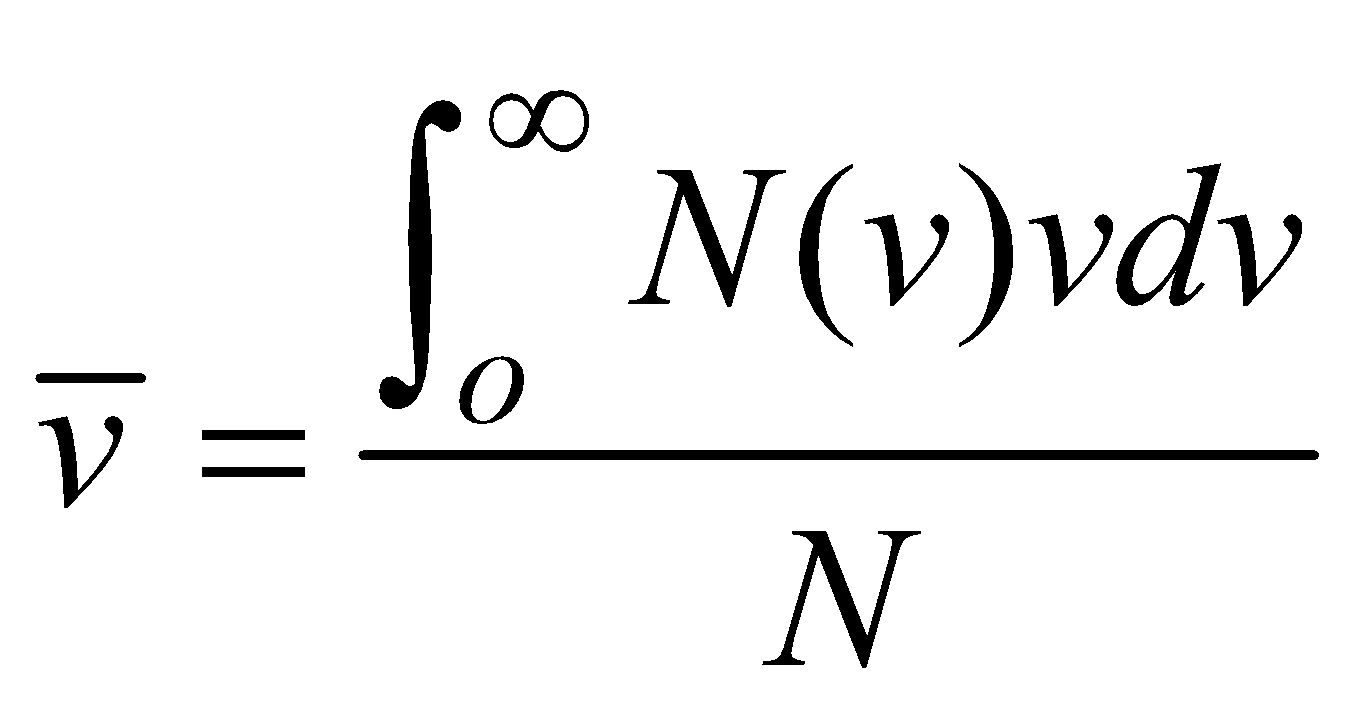 (where summation is replaced by integration because N is large)
(where summation is replaced by integration because N is large) ROOT MEAN SQUARE SPEED
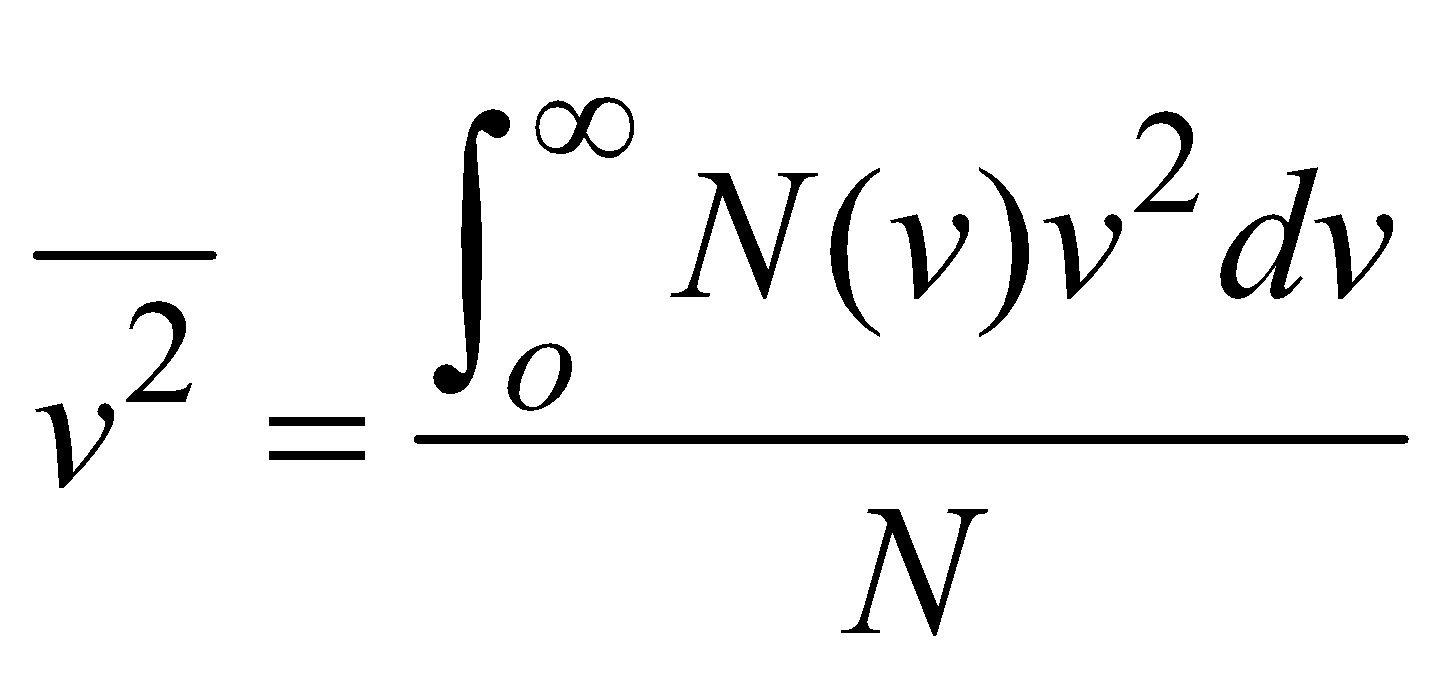 ….(2)
….(2)MOST PROBABLE SPEED
- Brownian motion, provides a direct evidence for the existence of molecules and their motion. The zig-zag motion of gas molecules is Brownian motion.
- Average speed
- Root mean square speed,
- Most probable speed
- Vrms :
 : Vmp = 1.73 : 1.60 : 1.41
: Vmp = 1.73 : 1.60 : 1.41
Worked Out Examples
Ideal Gases
3.2.1 State the macroscopic gas laws relating pressure, volume and temperature.
Boyle’s Law – For a gas at a constant temperature the volume and the pressure are inversely proportional:
(1)
| Plotting pressure vs. volume produces the following graph: | Plotting pressure vs. inverse volume produces a straight line graph: |
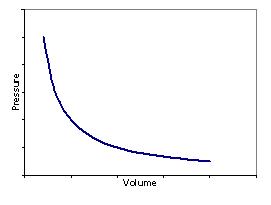 | 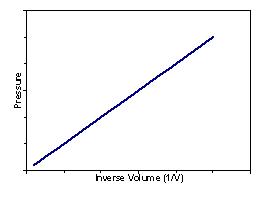 |
If a thermodynamic system changes, but its temperature remains constant then the following the initial pressure and volume are related to the final pressure and volume by the following equation:
(2)
Charles’ Law – If the mass and pressure of a gas are held constant, the volume of the gas is directly proportional to its absolute temperature.
(3)
If a thermodynamic system changes, but its mass and pressure are held constant the initial volume and temperature are related to the final volume and temperature by the following equation:
(4)
Gay-Lussac’s Law ¬– If the volume of a sample of gas remains constant, the absolute pressure of the gas is directly proportional to its absolute temperature.
(5)
If a thermodynamic system changes, but the volume are held constant the initial pressure and temperature are related to the final pressure and temperature by the following equation:
(6)
All of the above mentioned laws required special circumstances that are not often satisfied. A more general relationship between the volume, pressure and temperature can be found:
(7)
This still does not take into account a change in mass. If the temperature and pressure of a gas is held constant and more gas is added (mass increases) the volume must increase. If the volume and temperature of a gas are held constant while more gas is added the pressure must increase. If we combine these experimental observations we can write an even more general relation:
(8)
3.2.2 Define the terms mole and molar mass
In general we use relatively small amount of gas or just a few numbers of atoms or molecules. It is possible to determine the mass of individual atoms or molecules, but the numbers are messy, a gram is an incredibly large mass compared to the mass of an atom. So we define a new mass unit, called an atomic mass unit or amu.
An atomic mass unit is defined as 1/12th the mass of a carbon-12 atom. Basically the mass of a proton or neutron, or a proton or neutron have mass 1 amu. Note: Neutrons and protons do not have exactly the same mass, but its close enough. Thus one carbon-12 atom has mass 12 amu.
Helium-4 has an mass 4 amu or approximately and fluorine-19 has a mass of 19 amu or approximately $1.99 \times 10^{-23} g$. Which numbers would you rather use?
It would be a rare find to find a scale that measures in amu. So how do we relate amu to grams? Here we define the concept of a mole. A mole (mol) is the number of particles in a sample such that the mass in grams of the sample is equal to the mass in amu of a single particle. So 1 mol of carbon-12 atoms has a mass of 12 g, 1 mol of helium-4 has a mass of 4 g.
From this we can define the concept of molar mass, this is simply the grams per mole. Carbon-12’s molar mass is $12g \cdot mol^-1$.
3.2.3 Define the Avogadro constant
One day some body got bored and wondered exactly how many particles are in a mole, this guy’s name was Avogadro (written in symbol form NA). I don’t think he actually made a good measurement of his number, but hey he got a symbol named after him, better than I could do.
(9)
This number is called Avogadro’s number of Avogadro’s constant. The accepted value is:
(10)
3.2.4 State that the equation of state of an ideal gas is
The number of moles of gas to the mass of gas is related by the molecular mass of the gas. Therefore we can write the mass as:
(11)
Where m is the mass, n is the number of moles and M is the molecular mass. If we substitute this expression in to the general gas law:
3.2.1 State the macroscopic gas laws relating pressure, volume and temperature.
Boyle’s Law – For a gas at a constant temperature the volume and the pressure are inversely proportional:
(12)
| Plotting pressure vs. volume produces the following graph: | Plotting pressure vs. inverse volume produces a straight line graph: |
 |  |
If a thermodynamic system changes, but its temperature remains constant then the following the initial pressure and volume are related to the final pressure and volume by the following equation:
(13)
Charles’ Law – If the mass and pressure of a gas are held constant, the volume of the gas is directly proportional to its absolute temperature.
(14)
If a thermodynamic system changes, but its mass and pressure are held constant the initial volume and temperature are related to the final volume and temperature by the following equation:
(15)
Gay-Lussac’s Law ¬– If the volume of a sample of gas remains constant, the absolute pressure of the gas is directly proportional to its absolute temperature.
(16)
If a thermodynamic system changes, but the volume are held constant the initial pressure and temperature are related to the final pressure and temperature by the following equation:
(17)
All of the above mentioned laws required special circumstances that are not often satisfied. A more general relationship between the volume, pressure and temperature can be found:
(18)
This still does not take into account a change in mass. If the temperature and pressure of a gas is held constant and more gas is added (mass increases) the volume must increase. If the volume and temperature of a gas are held constant while more gas is added the pressure must increase. If we combine these experimental observations we can write an even more general relation:
(19)
Assuming the molecular mass is constant:
(20)
This can be written yet again as:
(21)
Or as the ideal gas law:
(22)
An ideal gas being a gas that obeys the ideal gas law at all pressures, volumes and temperatures. No real gas is ideal, but most gases obey the ideal gas law for low pressure and high temperatures (above their freezing point).
R is called the universal gas constant, the value of R is dependent on the choice of units:
(23)
The universal gas constant is given in the IB formula booklet.
3.2.5 Describe the concept of absolute zero and the Kelvin scale
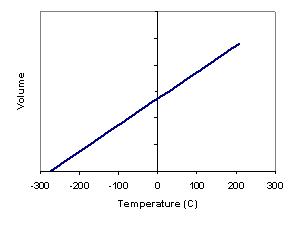
If the volume of a gas is measured at constant pressure but at different temperatures a linear relationship is found. If the line is extended to the left it will eventually intercept the temperature axis, if the line went farther than this it would represent a negative volume which does not make physical sense. If lines are plotted for several different gases it can be found that they have different slopes, but intercept the temperature axis at the same point. This temperature is in theory a minimum temperature, or absolute zero. Absolute zero does not mean there is no internal energy, but only that internal energy is at a minimum.
It should be noticed also that the equations presented above would provide nonsensical answers for negative temperatures, i.e. negative volume or negative pressure. This is simply a mathematical issue. Due to this, a new scale the Kelvin scale was developed where 0 K is absolute zero. One degree Kelvin is the same change in temperature as one degree Celsius. 0 K is defined as -273.16°C, for the purposes of the IB -273°C is sufficient.
3.2.6 Solve problems using the equation of state of an ideal gas
3.2.7 Describe the kinetic model of an ideal gas
3.2.8 Explain the macroscopic behavior of an ideal gas in terms of molecular model
The assumptions or postulates of the moving particle theory are extended for an ideal gas to include:
- Gases consist of tiny particles called atoms (monatomic gases such as neon and argon) or molecules.
- The total number of molecules in any sample of gas is extremely large.
- The molecules are in constant random motion.
- The range of the intermolecular forces is small compared to the average separation of the molecules.
- The size of the particles is relatively small compared with the distance between them.
- Collisions of short duration occur between molecules and the walls of the container and the collisions are perfectly elastic.
- No forces act between particles except when they collide, and hence particles move in straight lines.
- Between collisions the molecules, obey Newton’s Laws of motion
The view of an ideal gas is one of molecules moving in random straight line paths at constant speeds until they collide with the sides of the container or with one another. Their paths over time are therefore zig-zags. Because the gas molecules can move freely and are relatively far apart, they occupy the total volume of a container.
The large number of particles ensures that the number of particles moving in all directions is constant at any time.
The pressure that the molecules exert is due to their collisions with the sides of the container. As the temperature of a gas is increased, the average kinetic energy per molecule increases. The increase in velocity of the molecules leads to a greater rate of collisions, and each collision involves greater impulse. Hence the pressure of the gas increases as the collisions with the sides of the container increase. When a force is applied to a piston in a cylinder containing a volume of gas, the molecules take up a smaller volume and hence collisions are more frequent leading to an increase in pressure.
Because the collisions are perfectly elastic there is no loss in kinetic energy as a result of the collisions. Temperature is a measure of the average kinetic energy per molecule.