10.1 Describing fields
Essential Idea:
Electric charges and masses each influence the space around them and that influence can be represented through the concept of fields.
Understandings:
- Gravitational fields
- Electrostatic fields
- Electric potential and gravitational potential
- Field lines
- Equipotential surfaces
Applications and Skills:
- Representing sources of mass and charge, lines of electric and gravitational force, and field patterns using an appropriate symbolism
- Mapping fields using potential
- Describing the connection between equipotential surfaces and field lines
Data booklet reference:
- /\(W=q\Delta V_e\)
- \(W=m\Delta V_g\)
ELECTRIC FIELD
The space around an electric charge, where it exerts a force on another charge is an electric field.
Electric force, like the gravitational force acts between the bodies that are not in contact with each other. To understand these forces, we involve the concept of force field. When a mass is present somewhere, the properties of space in vicinity can be considered to be so altered in such a way that another mass brought to this region will experience a force there. The space where alteration is caused by a mass is called its Gravitational field and any other mass is thought of as interacting with the field and not directly with the mass responsible for it.
Similarly an electric charge produces an electric field around it so that it interacts with any other charges present there. One reason it is preferable not to think of two charges as exerting forces upon each other directly is that if one of them is changed in magnitude or position, the consequent change in the forces each experiences does not occur immediately but takes a definite time to be established. This delay cannot be understood on the basis of coulomb law but can be explained by assuming (using field concept) that changes in field travel with a finite speed. (≈ 3 × 108 m / sec).
Electric field can be represented by field lines or line of force.
The direction of the field at any point is taken as the direction of the force on a positive charge at the point.
Electric field intensity due to a charge q at any position (![]() ) from that charge is defined as
) from that charge is defined as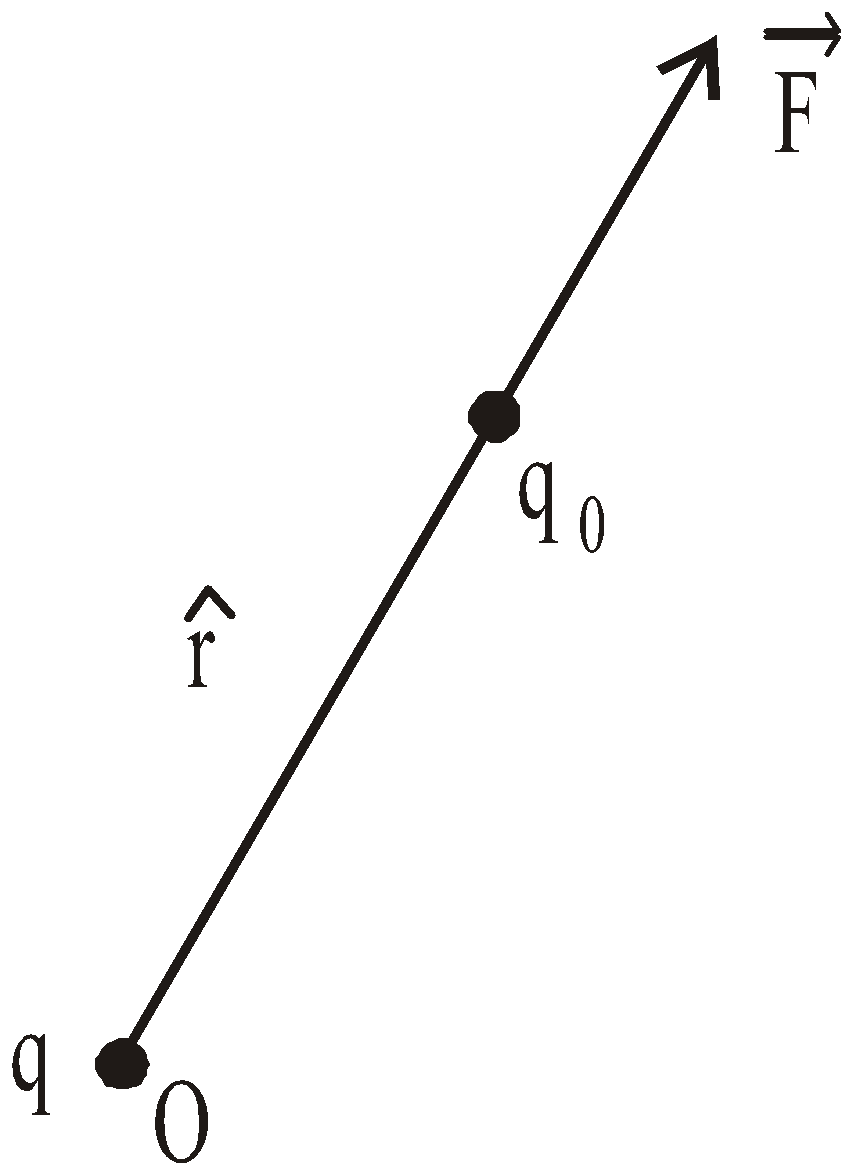
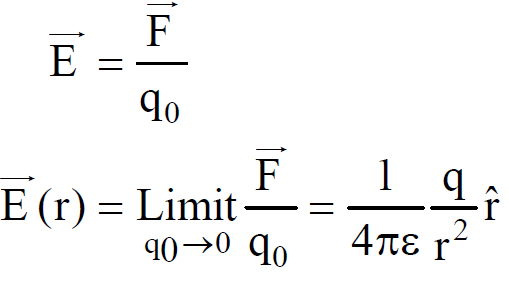
where ![]() is the force experienced by a small positive test charge q0 due to charge q.
is the force experienced by a small positive test charge q0 due to charge q.
Its SI unit is NC–1. It is a vector quantity.
If there are more charges responsible for the field, then ![]()
where ![]() are the electric field intensities due to charges q1, q2, q3…..respectively.
are the electric field intensities due to charges q1, q2, q3…..respectively.
ELECTRIC LINES OF FORCE
These are the imaginary lines of force and the tangent at any point on the lines of force gives the direction of the electric field at that point.
PROPERTIES OF ELECTRIC LINES OF FORCE
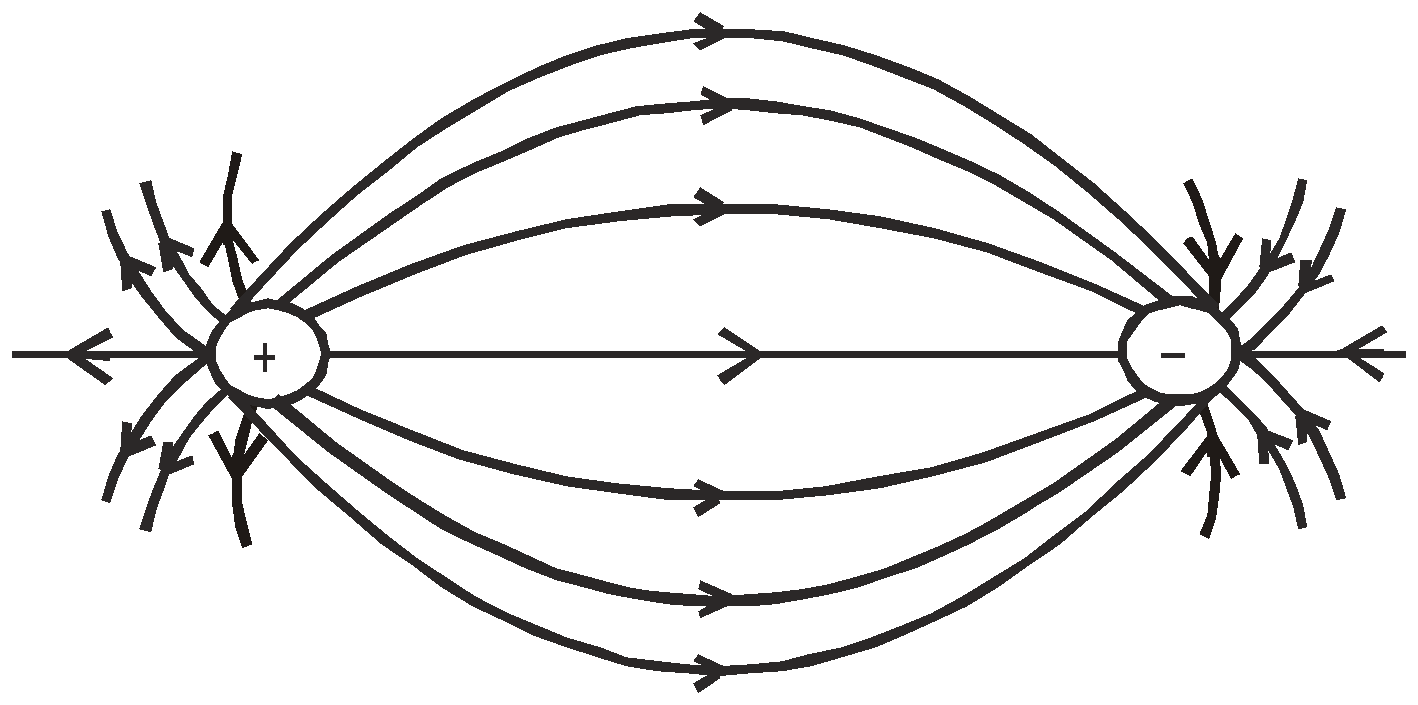
- The lines of force diverge out from a positive charge and converge at a negative charge. i.e. the lines of force are always directed from higher to lower potential.

- The electric lines of force contract length wise indicating unlike charges attract each other and expand laterally indicating like charges repel each other.
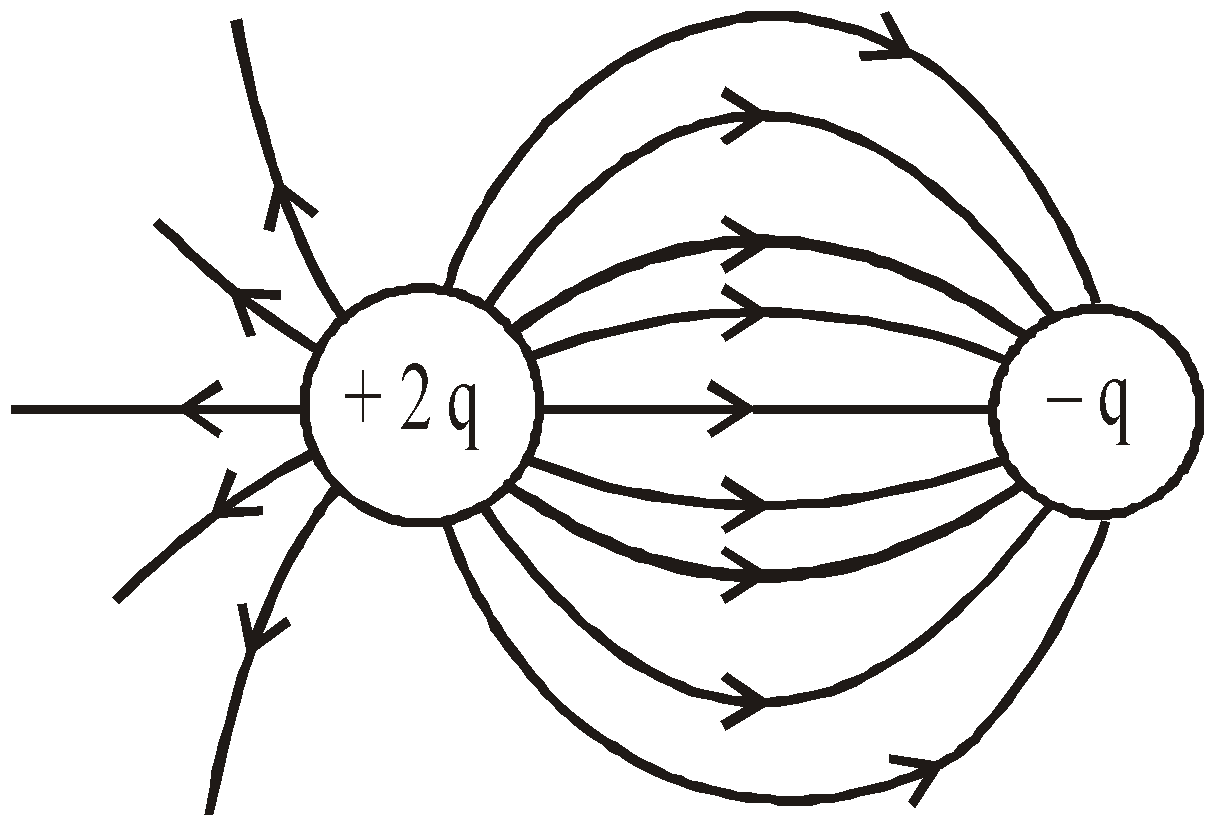
- The number of lines that originate from or terminate on a charge is proportional to the magnitude of charge.
i.e., ![]()
- Two electric lines of force never intersect each other.
- They begin from positive charge and end on negative charge i.e., they do not make closed loop (while magnetic field lines form closed loop).
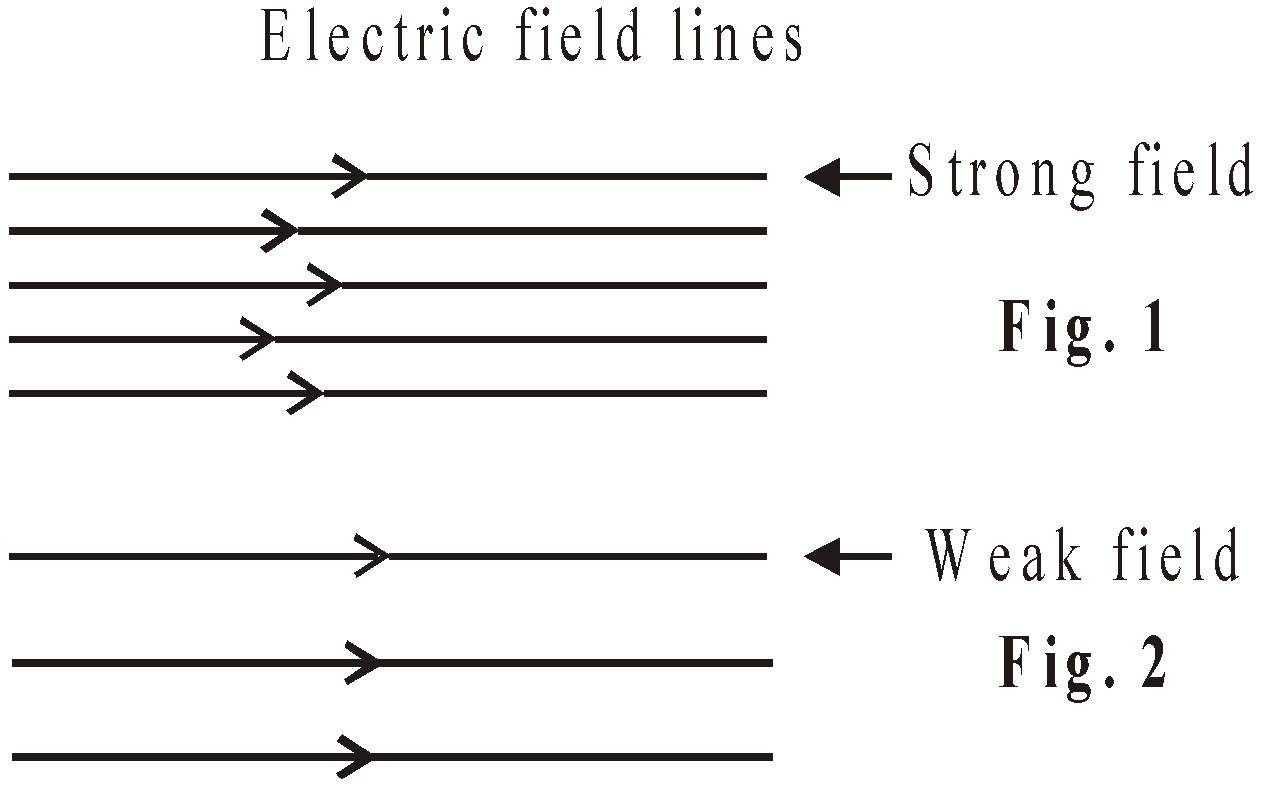
- Where the electric lines of force are
- close together, the field is strong (see fig.1)
- far apart, the field is weak (see fig.2)
- Electric lines of force generate or terminate at charges /surfaces at right angles.
ELECTRIC FIELD FOR CONTINUOUS CHARGE DISTRIBUTION
If the charge distribution is continuous, then the electric field strength at any point may be calculated by dividing the charge into infinitesimal elements. If dq is the small element of charge within the charge distribution, then the electric field at point P at a distance r from charge element dq is
Non conducting sphere (dq is small charge element)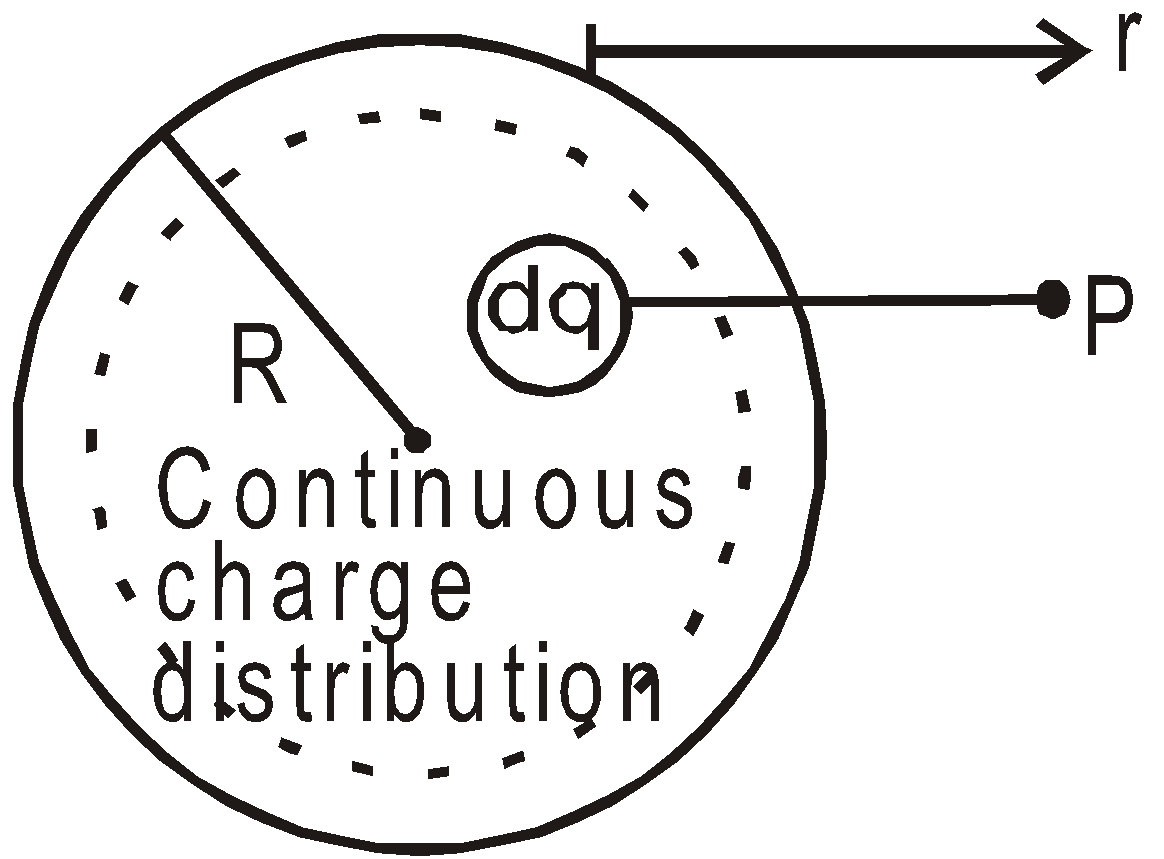
dq = λdl (line charge density)
= σ ds (surface charge density)
= ρdv (volume charge density)
The net field strength due to entire charge distribution is given by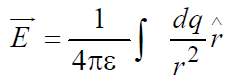
where the integration extends over the entire charge distribution.
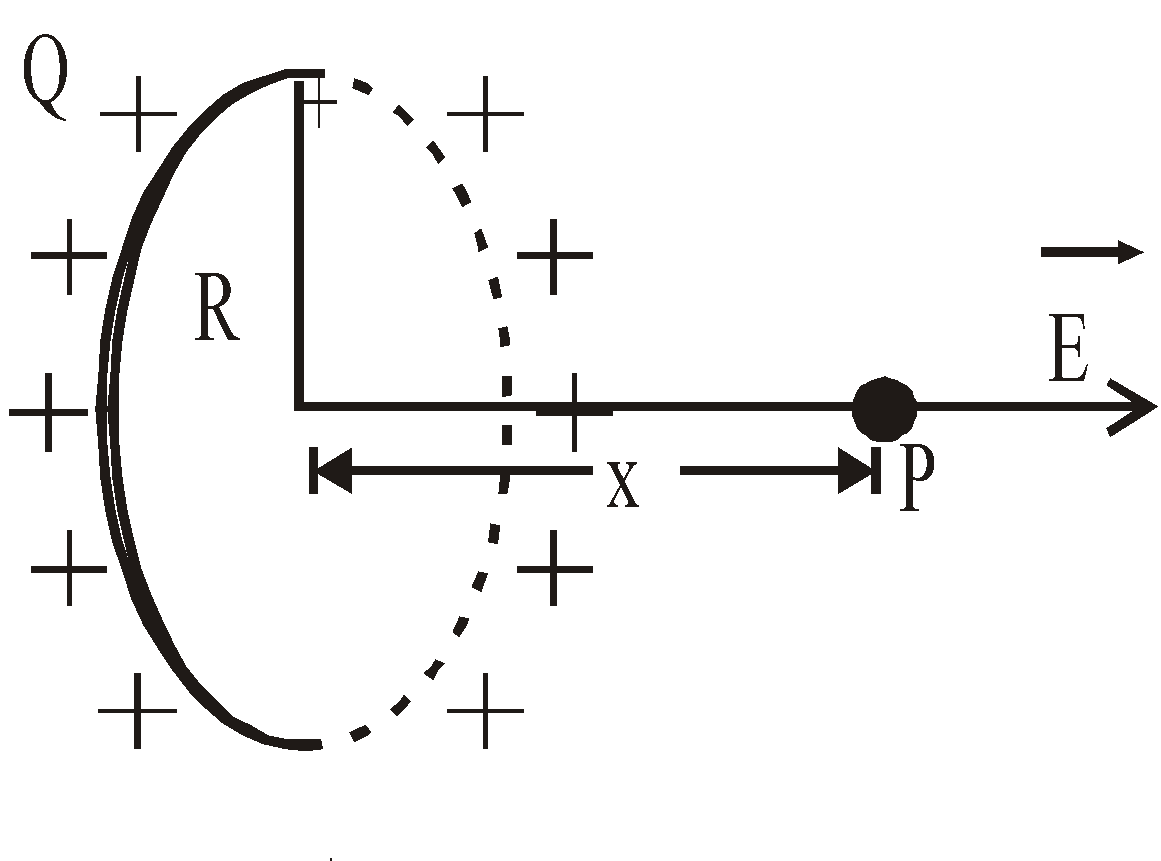
Note:- Electric field intensity due to a point charge q, at a distance (r1 + r2) where r1 is the thickness of medium of dielectric constant K1 and r2 is the thickness of medium of dielectric constant K2 as shown in fig. is given by![]()
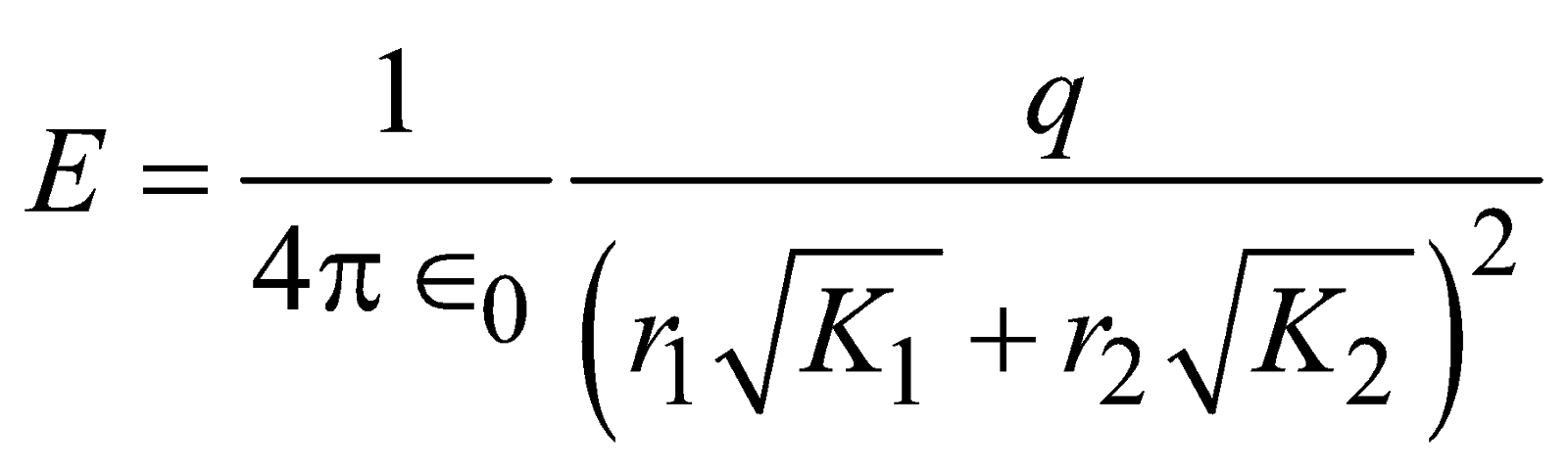
CALCULATION OF ELECTRIC FIELD INTENSITY FOR A DISTRIBUTION OF DIRECT AND CONTINUOUS CHARGE
- Fix origin of the coordinate system where electric field intensity is to be found.
- Draw the direction of electric field intensity due to the surrounding charges considering one charge at a time.
- Resolve the electric field intensity in x and y-axis respectively and find ΣEx and ΣEy
- The resultant intensity is
 and
and 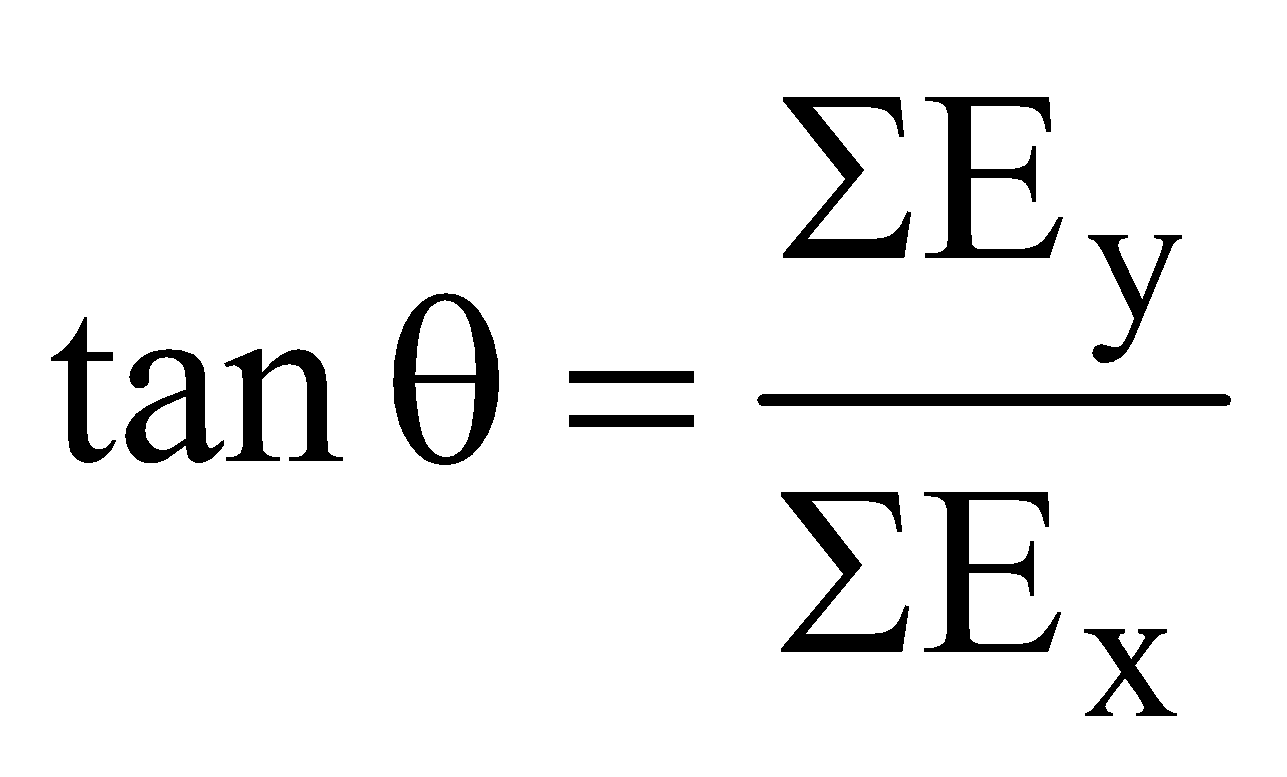 where θ is the angle between
where θ is the angle between  and x-axis.
and x-axis. - To find the force acting on the charge placed at the origin, the formula F = qE is used.
ENERGY DENSITY
Energy in unit volume of electric field is called energy density and is given by![]() ,
,
where E = electric field and εo= permittivity of vacuum
ELECTRIC FIELD DUE TO VARIOUS CHARGE DISTRIBUTION
- Electric Field due to an isolated point charge
![]()
![]()
- A circular ring of radius R with uniformly distributed charge
![]()
When x >> R, ![]()
[The charge on ring behaves as point charge]
E is max when ![]() . Also Emax
. Also Emax![]()
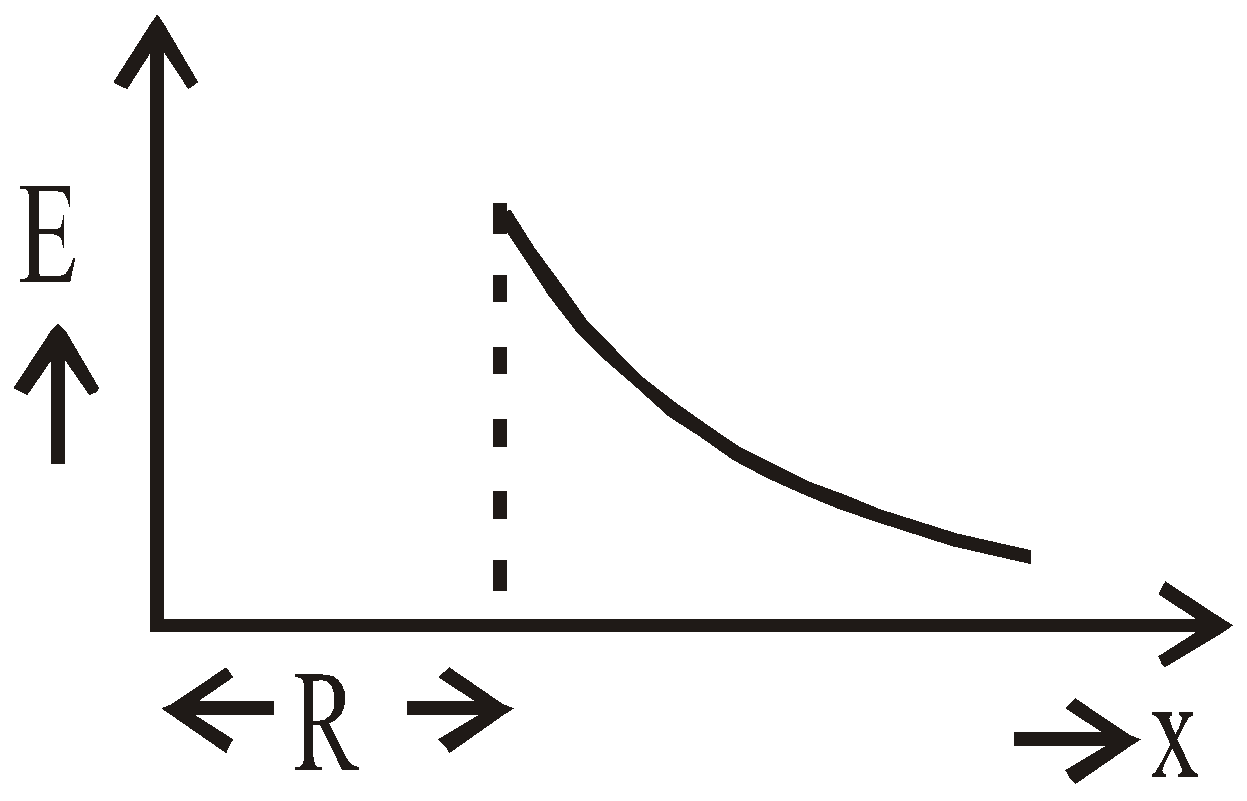
- A circular disc of radius R with uniformly distributed charge with surface charge density σ
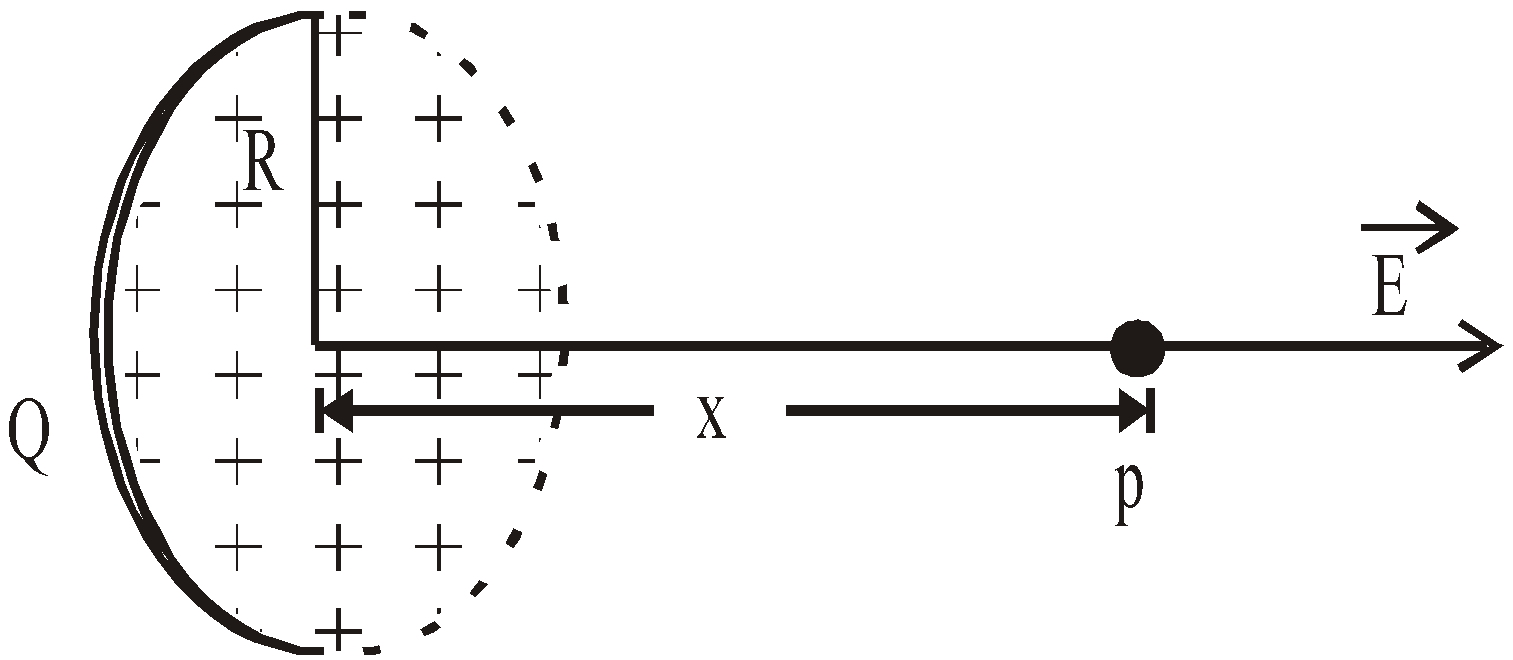
![]()
- An infinite sheet of uniformly distributed charges with surface charge density σ
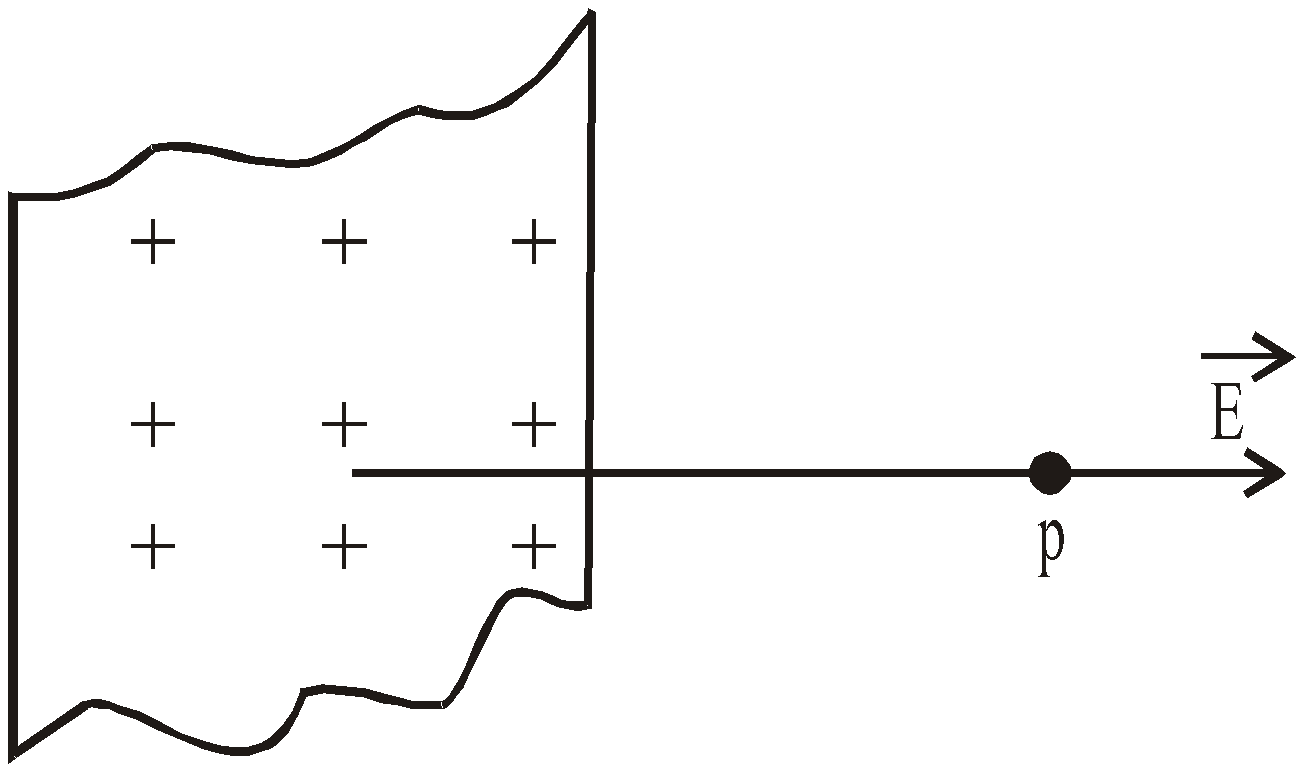
![]()
- A finite length of charge with linear charge density
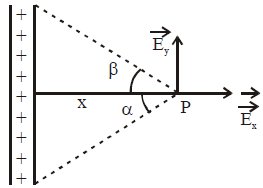
![]() and
and ![]()
Special case :
For Infinite length of charge, ![]()
∴ ![]() and
and ![]()
- Due to a spherical shell of uniformly distributed charges with surface charge density σ

Ein = 0 (x < R)![]()
![]()
- Due to a solid non conducting sphere of uniformly distributed charges with charge density ρ

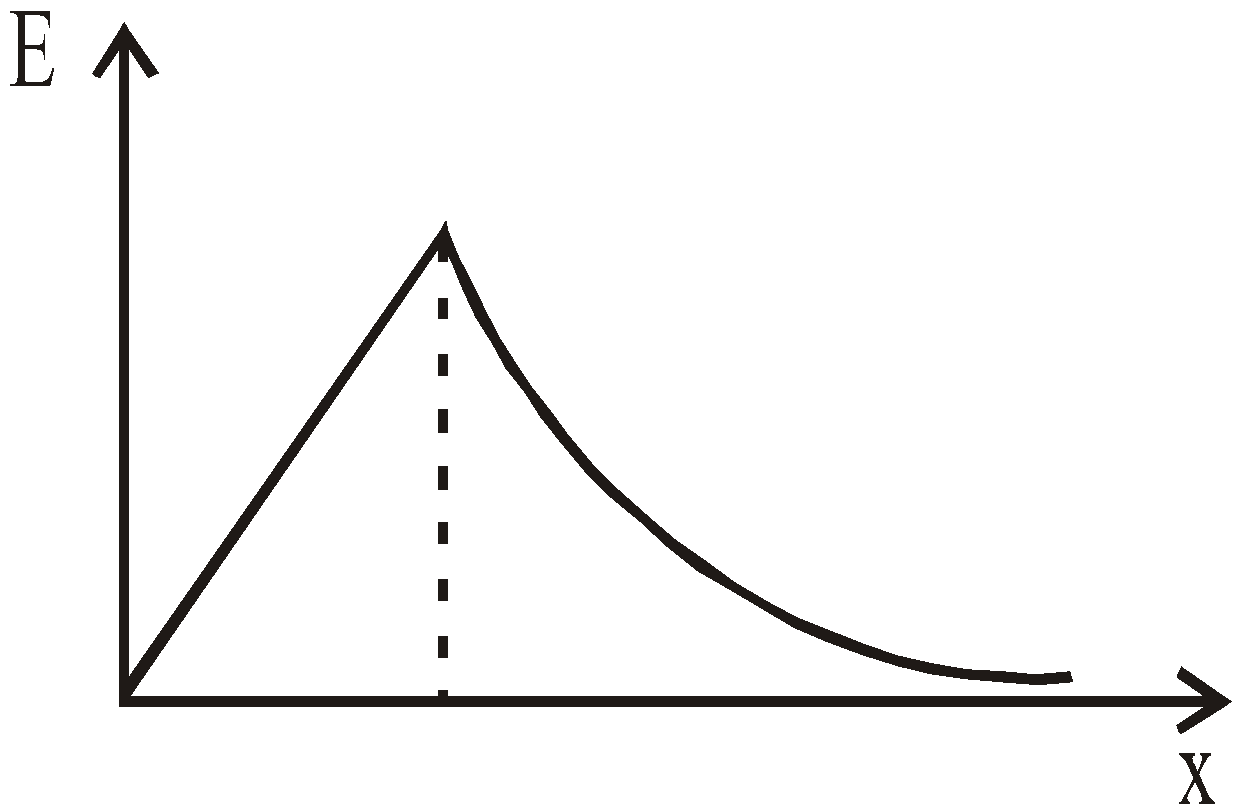
![]()
![]()
![]()
![]()
- Due to a solid non-conducting cylinder with linear charge density λ
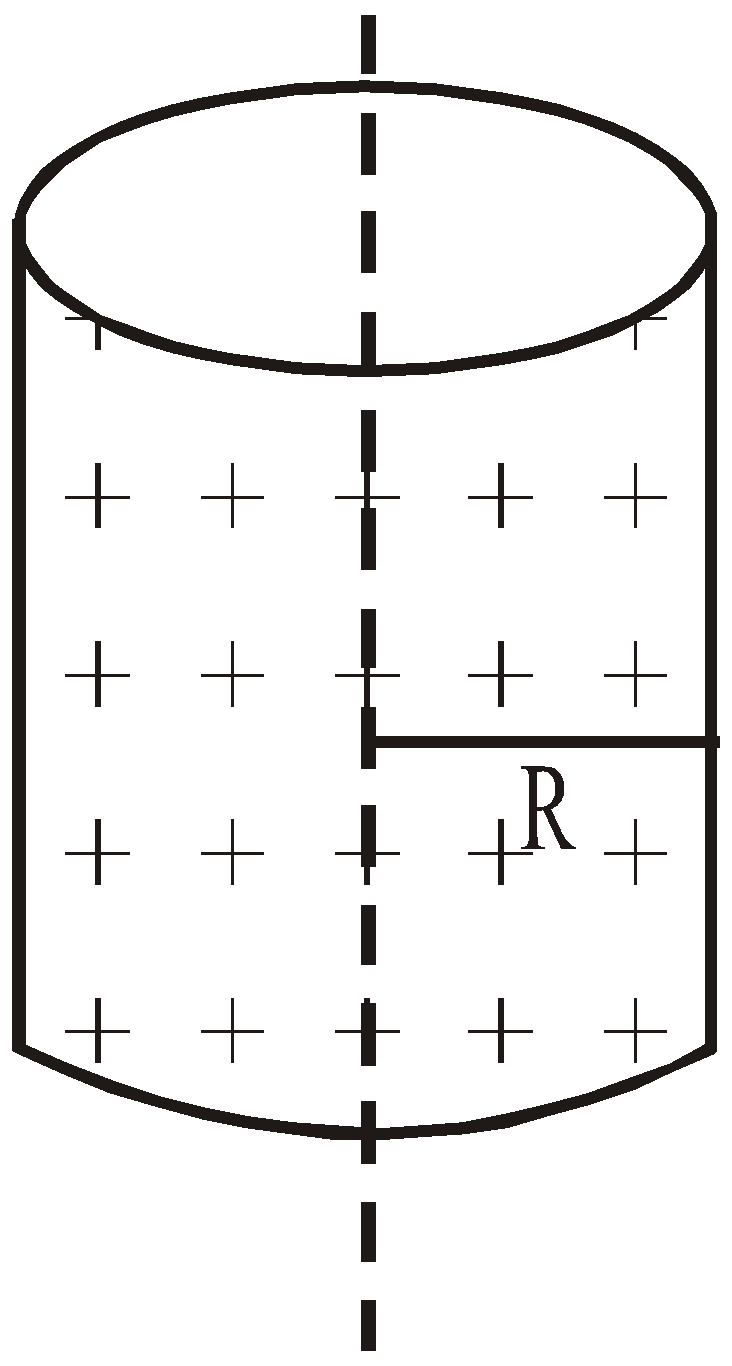
Eaxis = 0, ![]() ,
,![]() ,
,![]()
In above cases, ![]()
KEEP IN MEMORY
- If the electric lines of force are parallel and equally spaced, the field is uniform.
- If E0 and E be the electric field intensity at a point due to a point charge or a charge distribution in vacuum and in a medium of dielectric constant K then
E = KE0
- If E and E’ be the electric field intensity at a point in the two media having dielectric constant K and K’ then
![]()
- The electric field intensity at a point due to a ring with uniform charge distribution doesn’t depend upon the radius of the ring if the distance between the point and the centre of the ring is much greater than the radius of the ring. The ring simply behaves as a point charge.
- The electric field intensity inside a hollow sphere is zero but has a finite value at the surface
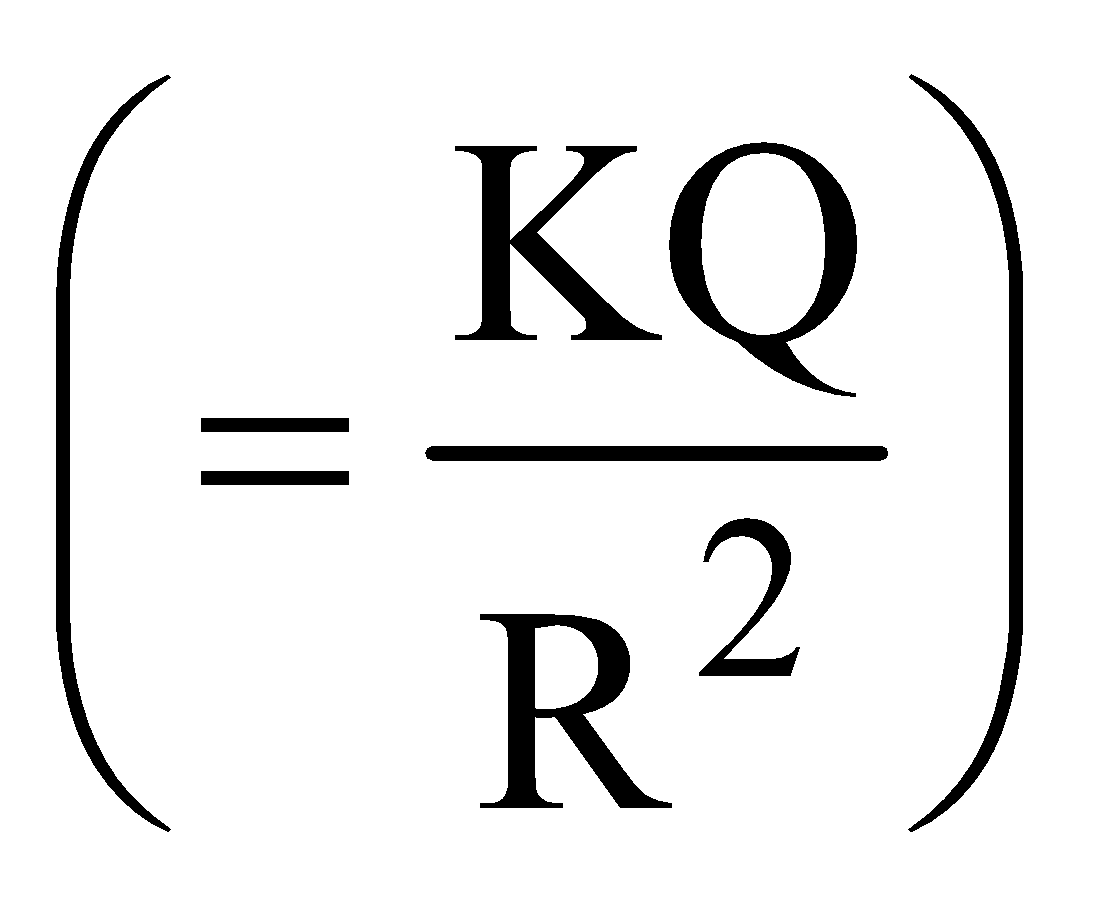 and outside it (
and outside it (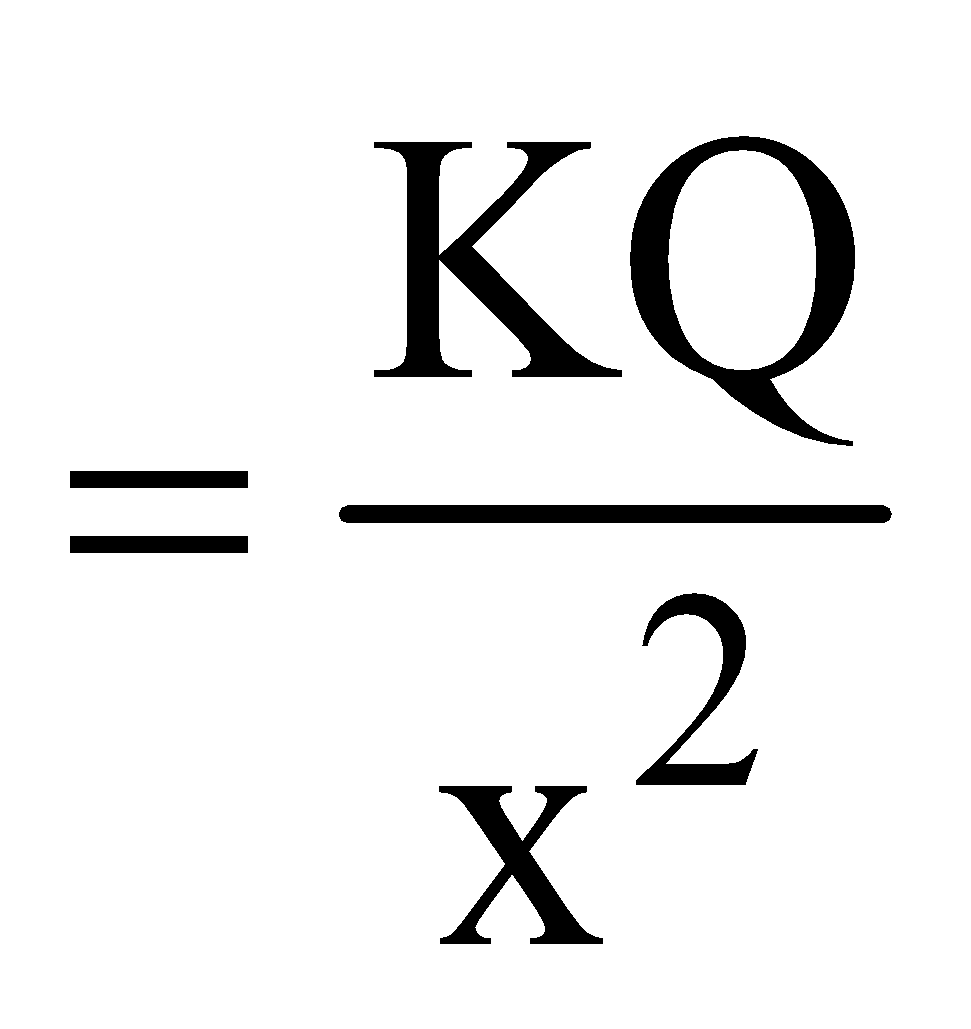 ; x being the distance of the point from the centre of the sphere).
; x being the distance of the point from the centre of the sphere). - The electric field intensity at a point outside a hollow sphere (or spherical shell) does not depend upon the radius of the sphere. It just behaves as a point charge.
- The electric field intensity at the centre of a non-conducting solid sphere with uniform charge distribution is zero. At other points inside it, the electric field varies directly with the distance from the centre (i.e. E ∝ x; x being the distance of the point from the centre). On the surface, it is constant but varies inversely with the square of the distance from the centre (i.e.
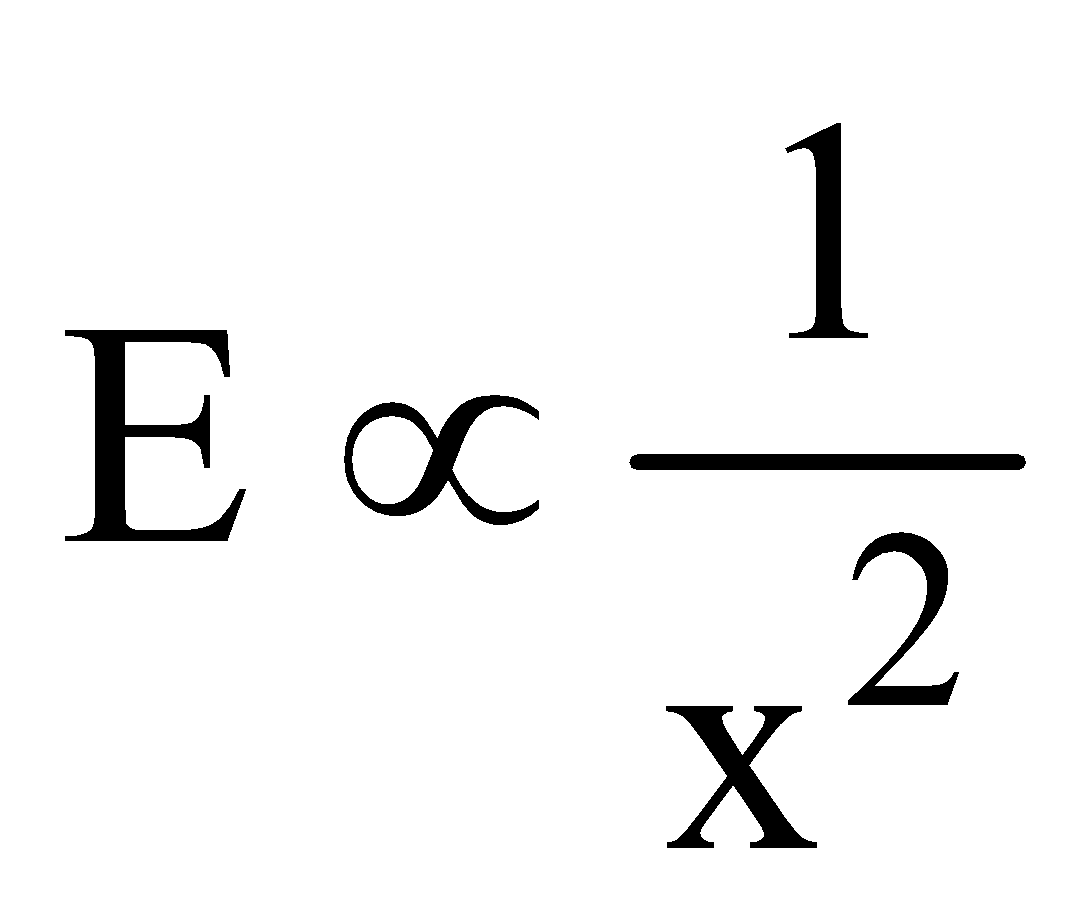 ). Note that the field doesn’t depend on the radius of the sphere for a point outside it. It simply behaves as a point charge.
). Note that the field doesn’t depend on the radius of the sphere for a point outside it. It simply behaves as a point charge. - The electric field intensity at a point on the axis of non-conducting solid cylinder is zero. It varies directly with the distance from the axis inside it (i.e. E ∝ x). On the surface, it is constant and varies inversely with the distance from the axis for a point outside it (i.e.
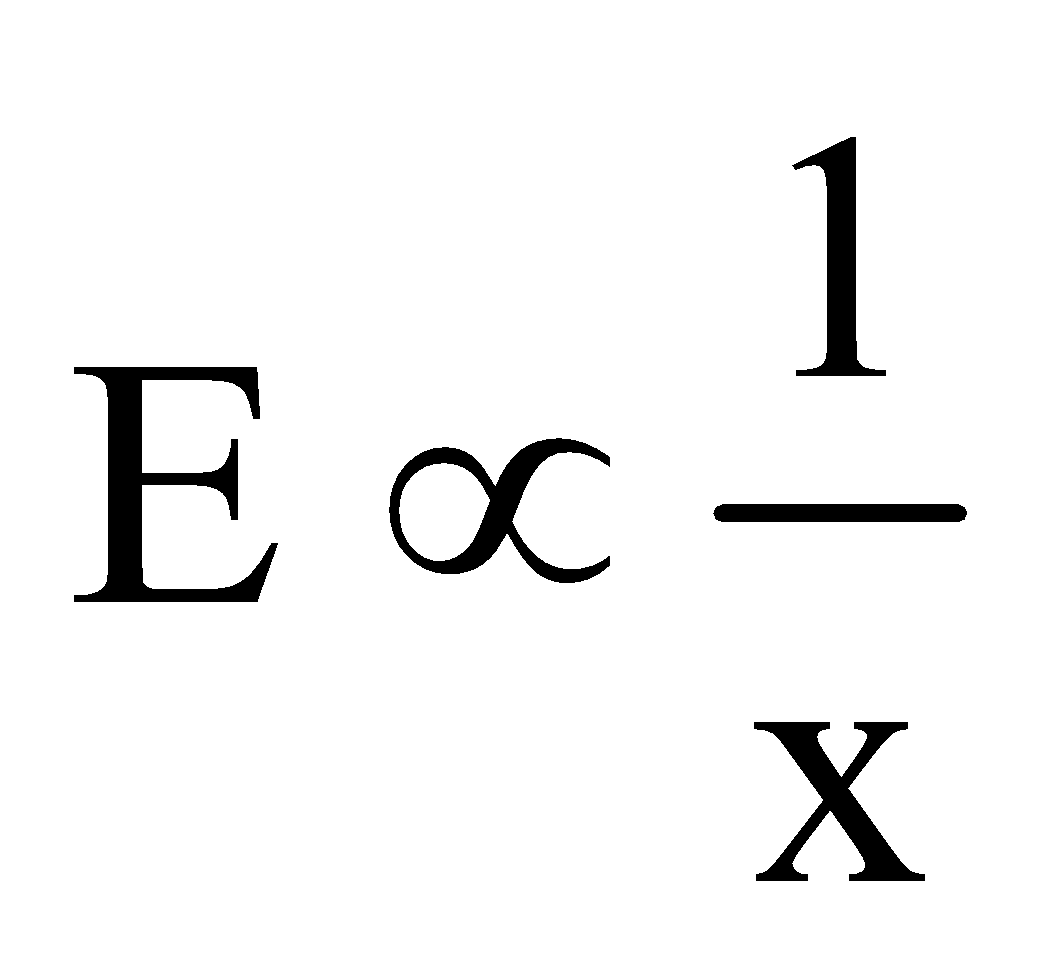 ).
).
MOTION OF A CHARGED PARTICLE IN AN ELECTRIC FIELD
Let a charged particle of mass m and charge q be placed in a uniform electric field![]() , then electric force on the charge particle is
, then electric force on the charge particle is ![]()
∴ acceleration, ![]() (constant)
(constant)
- The velocity of the charged particle at time t is,
v = u + at = at = ![]() (Particle initially at rest) or
(Particle initially at rest) or ![]()
- Distance travelled by particle is
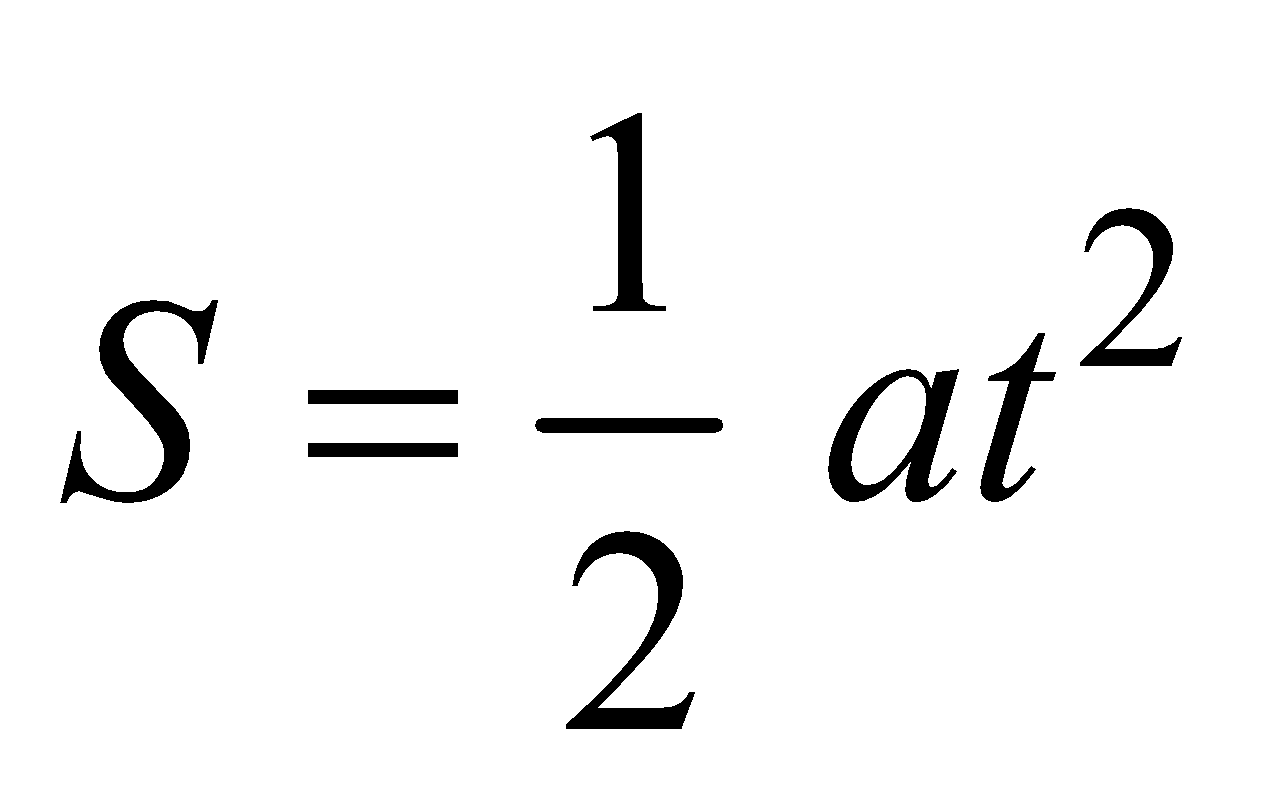

- Kinetic energy gained by particle,
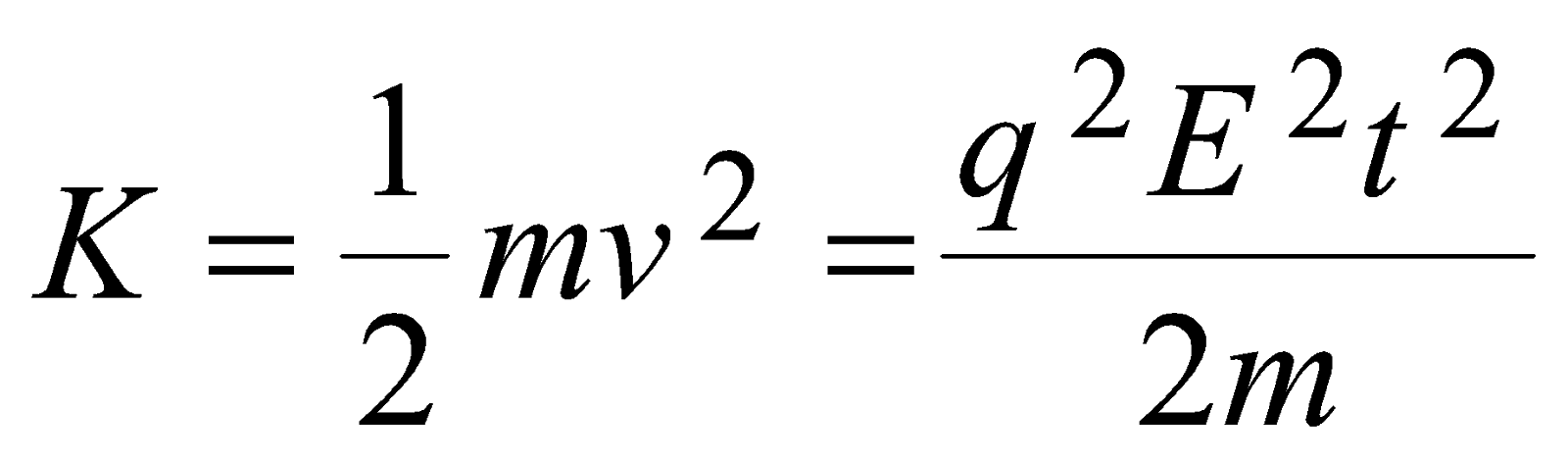
If a charged particle is entering the electric field in perpendicular direction.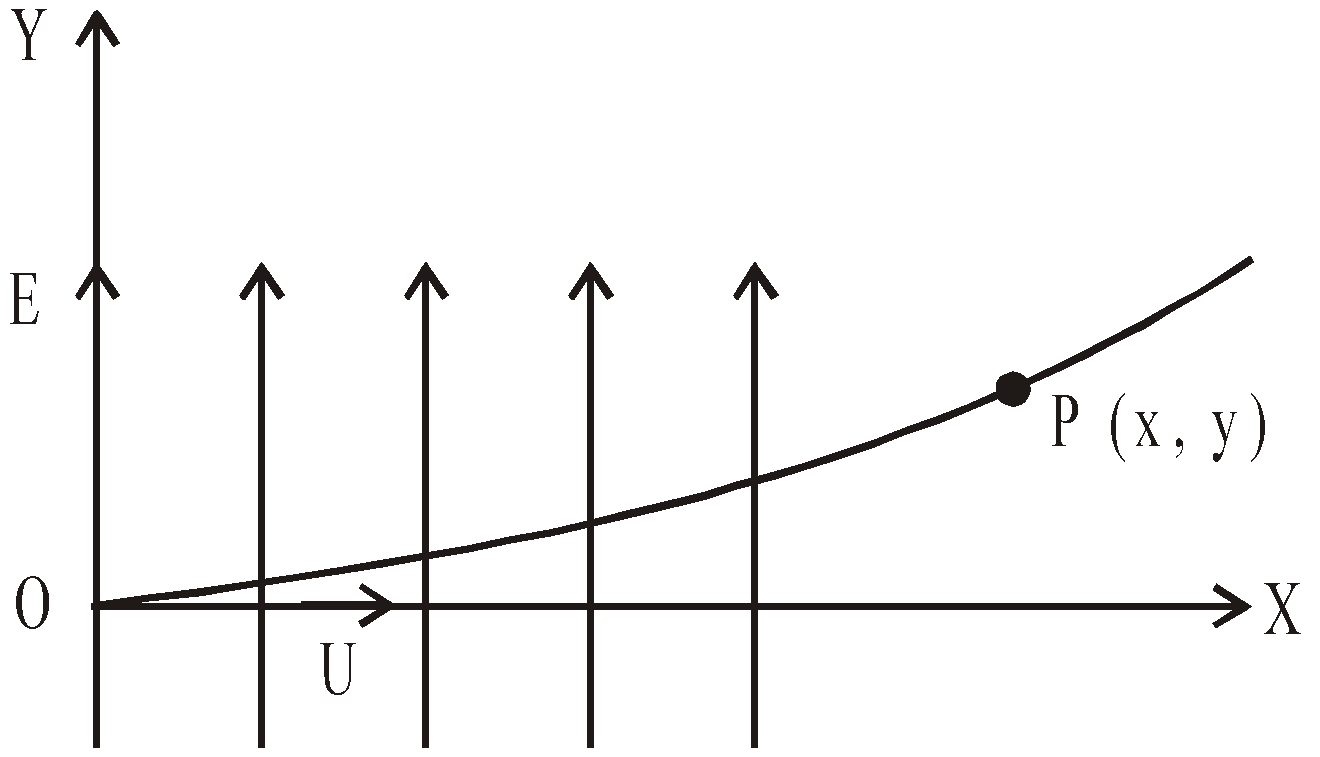
Let ![]() and the particle enters the field with speed u along x-axis.
and the particle enters the field with speed u along x-axis.
Acceleration along Y-axis, ![]()
The initial component of velocity along y-axis is zero. Hence the deflection of the particle along y-axis after time t is ;![]()
![]() …… (i)
…… (i)
Distance covered by particle in x-axis,
x = ut …… (ii) ( acceleration ax = 0)
Eliminating t from equation (i) & (ii),![]() i.e. y ∝ x2.
i.e. y ∝ x2.
This shows that the path of charged particle in perpendicular field is parabola.
If the width of the region in which the electric field exists be l then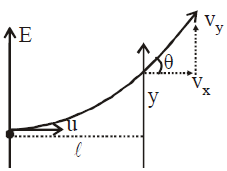
- the particle will leave the field at a distance from its original path in the direction of field, given by
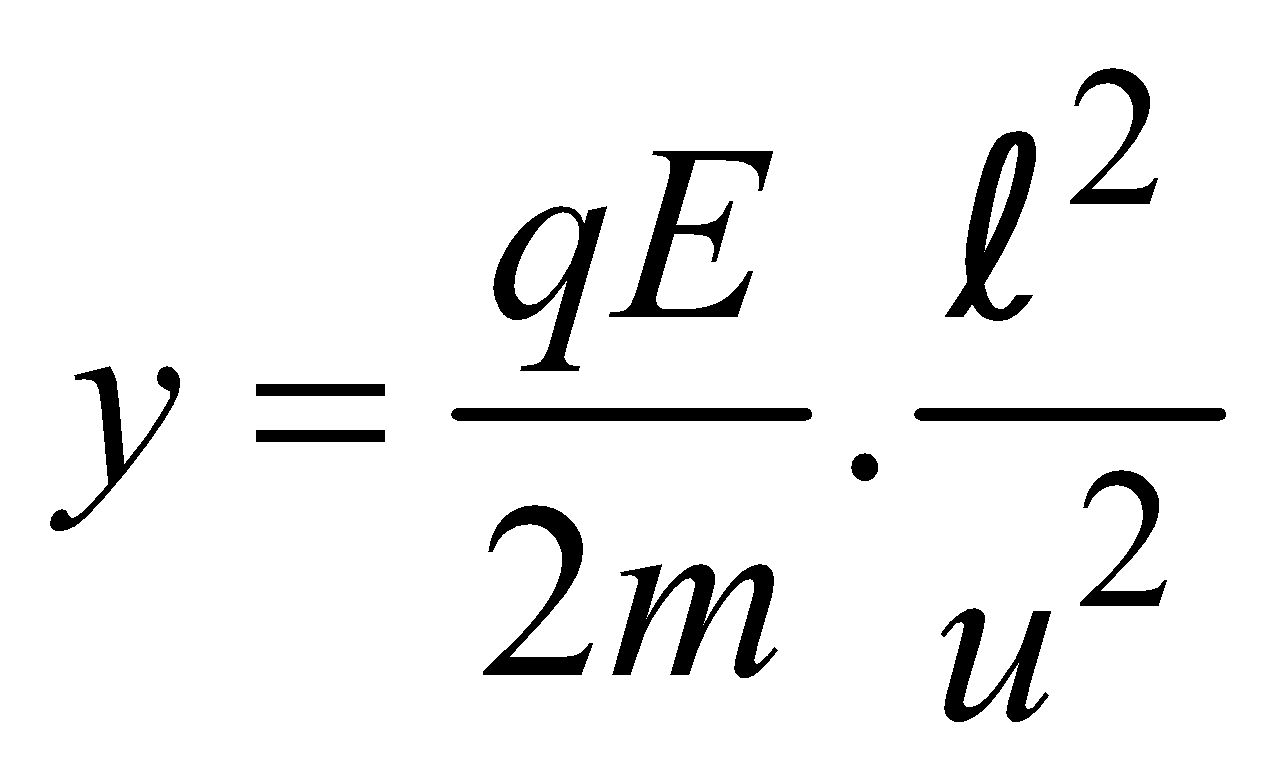
- The particle will leave the region in the direction of the tangent drawn to the parabola at the point of escape.
- The velocity of the particle at the point of escape is given b
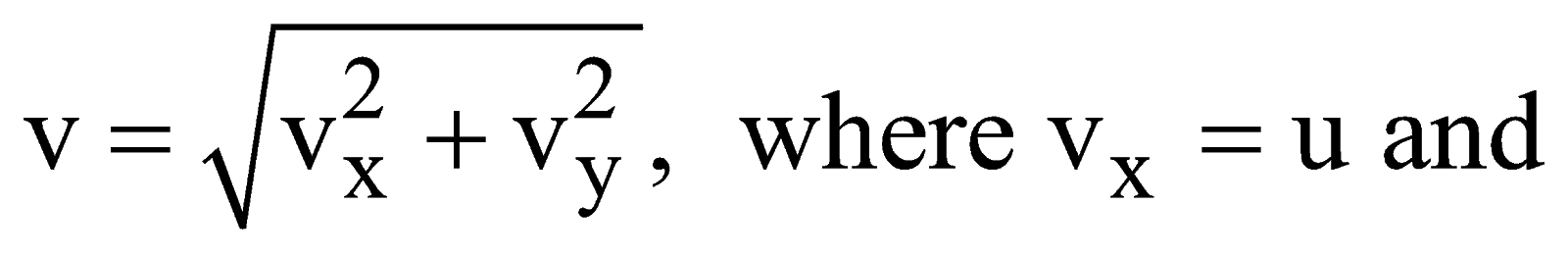

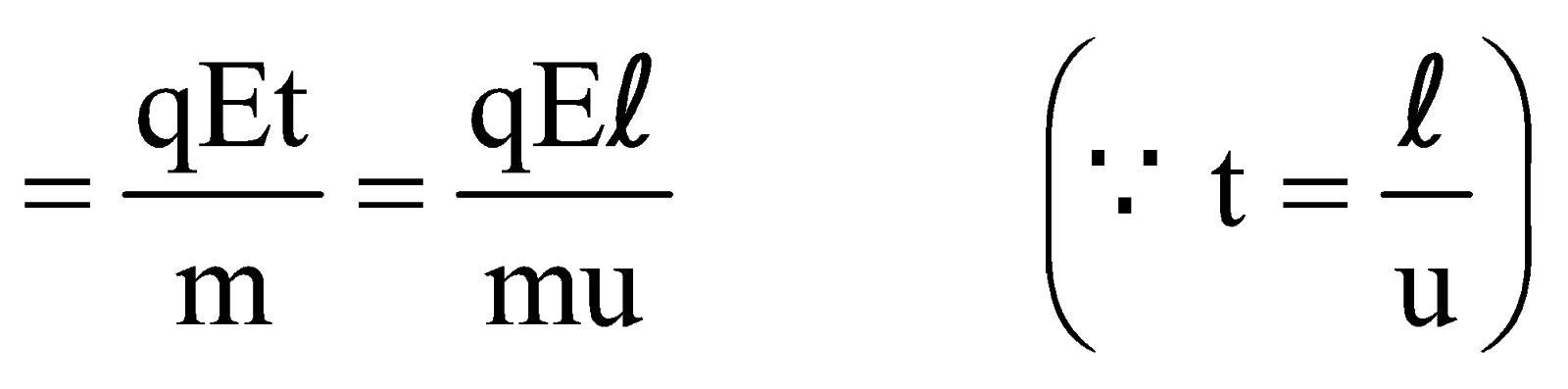
![]()
- The direction of the particle in which it leaves the field is given by
![]()
![]()
ELECTRIC DIPOLE
Two equal and opposite charges separated by a finite distance constitute an electric dipole. If –q and +q are charges at distance 2l apart, then dipole moment,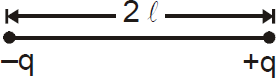
![]()
Its SI unit is coulomb metre.
Its direction is from –q to +q. It is a vector quantity.
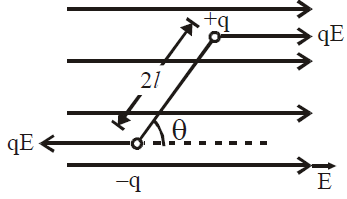
The torque τ on a dipole in uniform electric field as shown in figure is given by, ![]()
![]()
So τ is maximum, when dipole is ⊥ to field & minimum (=0) when dipole is parallel or antiparallel to field.
If ![]() and
and ![]()
Then 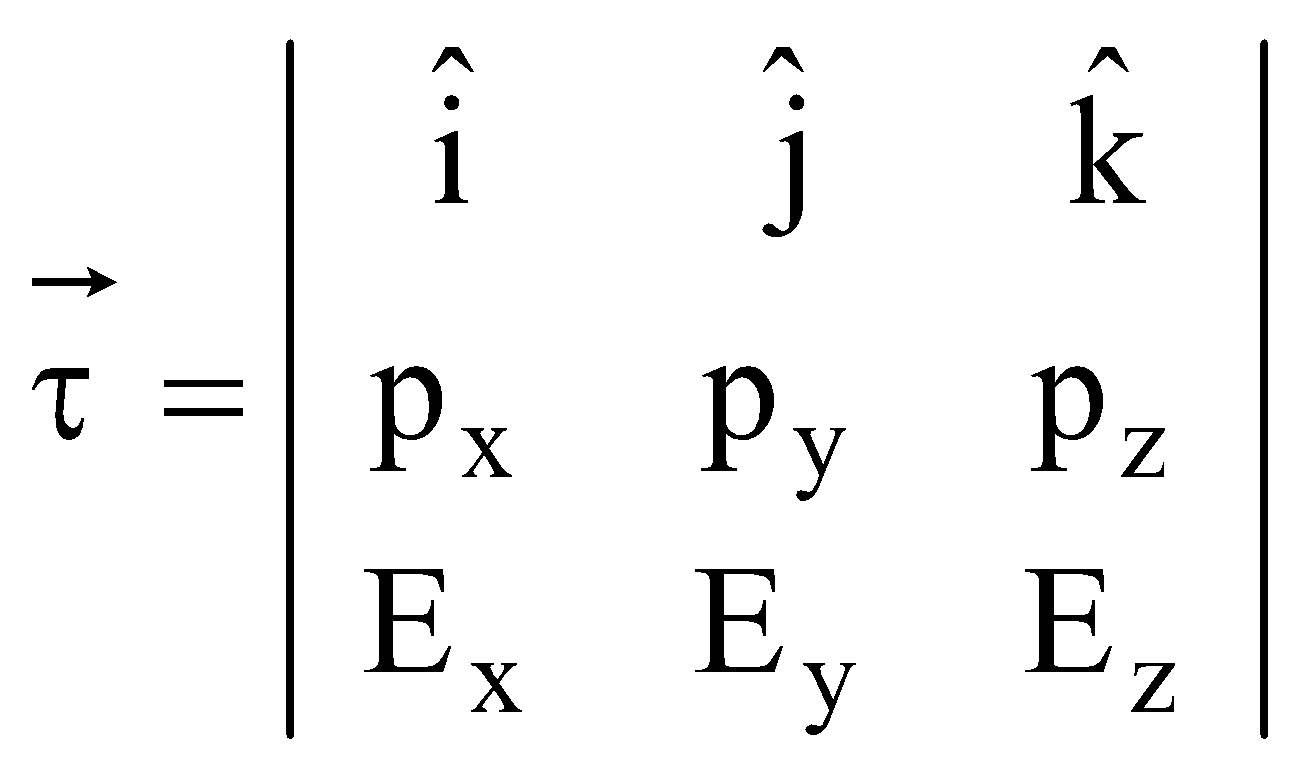
The work done in rotating the dipole from equilibrium through an angle dθ is given by![]()
and from θ1 → θ2, 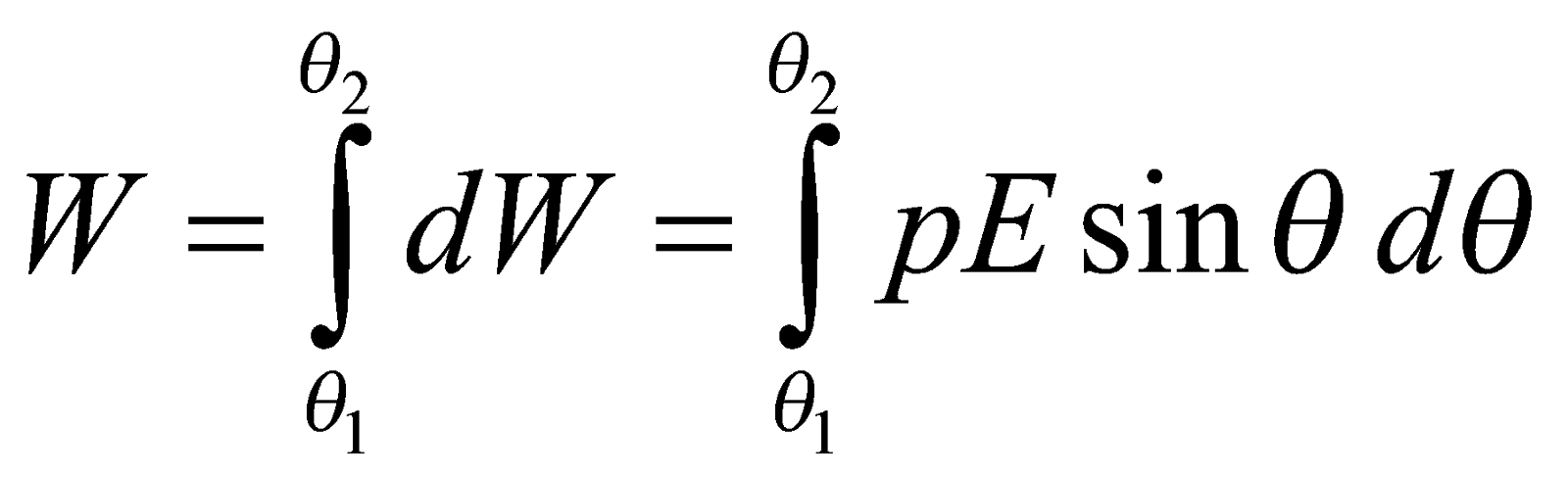
If θ1 = 0 i.e., equilibrium position, then![]()
Work done in rotating an electric dipole in uniform electric field from θ1 to θ2 is W = pE (cosθ1 – cosθ2)
Potential energy of an electric dipole in an electric field is,![]() i.e. U = –pE cosθ
i.e. U = –pE cosθ
where θ is the angle between![]() and
and ![]() .
.
We can also write ![]()
ELECTRIC FIELD DUE TO AN ELECTRIC DIPOLE
- Along the axial line (or end-on position)
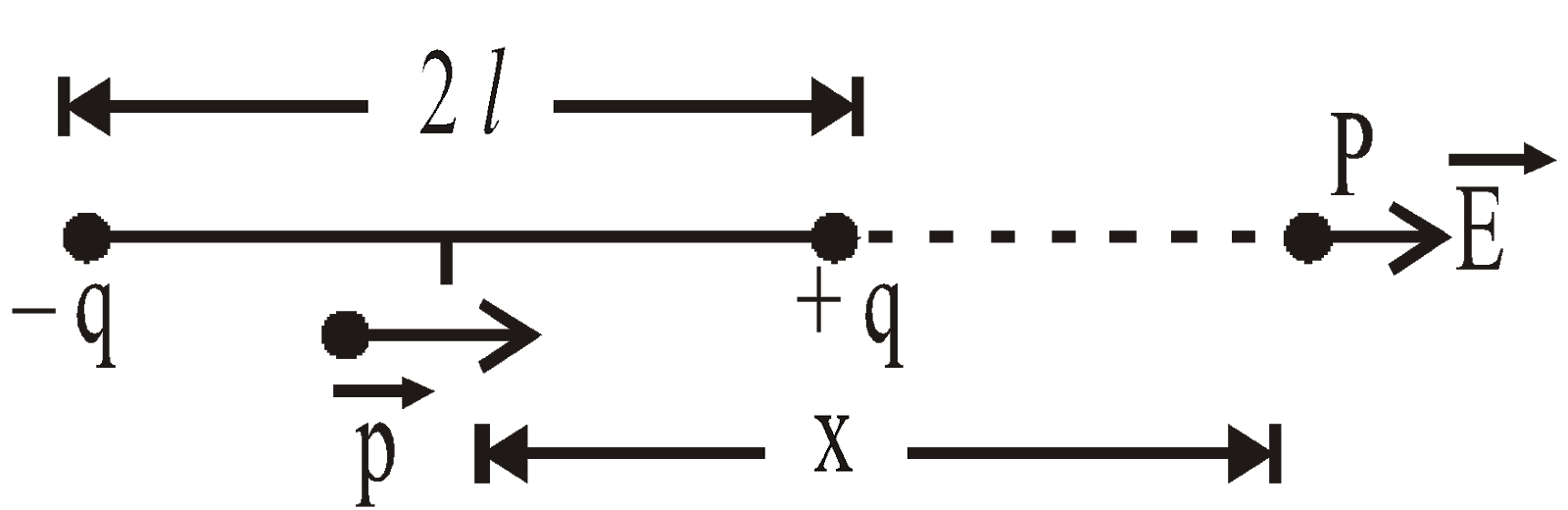
![]() and
and ![]() are parallel
are parallel![]() when x >> l
when x >> l
- Along equatorial line (or broadside on position)
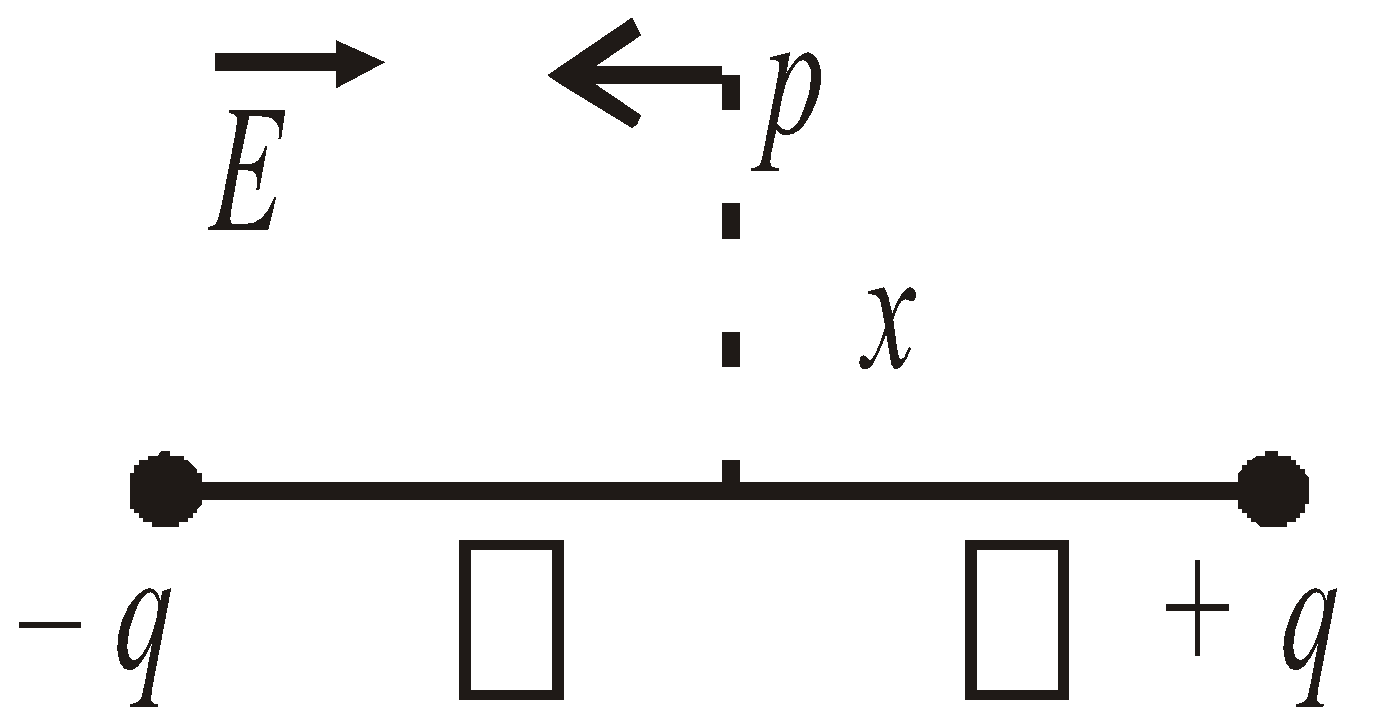
![]() when x >>l
when x >>l
When ![]() and
and ![]() are anti parallel then,
are anti parallel then,
Eax = 2 Eeq
- At any point (from the dipole)
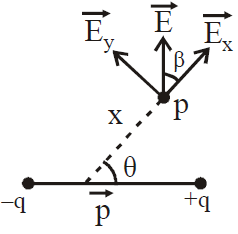
![]() ;
; ![]()
Electric field intensity due to a point charge varies inversely as cube of the distance and in case of quadrupole it varies inversely as the fourth power of distance from the quadrupole.
ELECTRIC FORCE BETWEEN TWO DIPOLES
The electrostatic force between two dipoles of dipole moments p1 and p2 lying at a separation r is![]() when dipoles are placed coaxially
when dipoles are placed coaxially![]() when dipoles are placed perpendicular to each other.
when dipoles are placed perpendicular to each other.
KEEP IN MEMORY
- The dipole moment of a dipole has a direction from the negative charge to the positive charge.
- If the separation between the charges of the dipole is increased (or decreased) K-times, the dipole moment increases (or decreases) by K-times.
- The torque experienced by a dipole placed in a uniform electric field has value always lying between zero and pE, where p is the dipole moment and E, the uniform electric field. It varies directly with the separation between the charges of the dipole.
- The work done in rotating a dipole in a uniform electric field varies from zero (minimum) to 2pE (maximum). Also, it varies directly with the separation between the charges of the dipole.
- The potential energy of the dipole in a uniform electric field always lies between +pE and –pE.
- The electric field intensity at a point due to an electric dipole varies inversely with the cube of the distance of the point from its centre if the distance is much greater than the length of the dipole.
- The electric field at a point due to a small dipole in end-on position is double of its value in broad side-on position,
i.e. EEnd-on = 2EBroad side-on
- For a small dipole, the electric field tends from infinity at a point very close to the axis of the dipole to zero at a point at infinity.
- The force between two dipoles increases (or decreases) by K4-times as the distance between them decreases (or increases) by K-times.
- Time period of a dipole in uniform electric field is
![]()
where I = moment of inertia of the dipole about the axis of rotation.
GRAVITATION
NEWTON’S UNIVERSAL LAW OF GRAVITATION
- The gravitational force is the central force and follows inverse square law. It acts along the line joining the particles.
- Since the work done by the gravitational force is independent of the path followed and hence it is a conservative force.
- It is the weakest force in nature. It is 1038 times smaller than nuclear force and 1036 times smaller than electric force. Strongest force being nuclear force (for small range) followed by electric force.
- Gravitation is independent of the presence of other bodies around it.
ACCELERATION DUE TO GRAVITY (g)
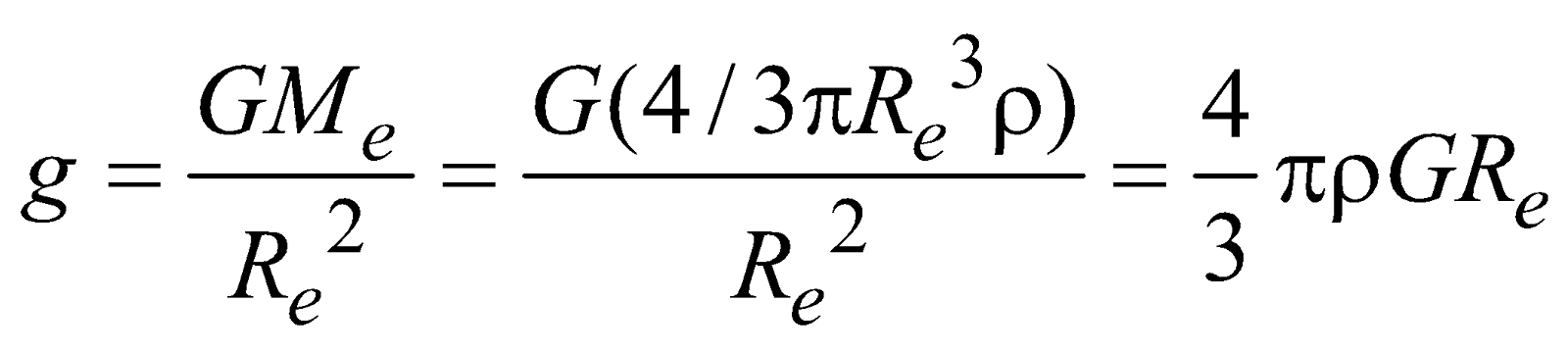 ……(iv)
……(iv)CHANGE IN THE VALUE OF ACCELERATION DUE TO GRAVITY (g)
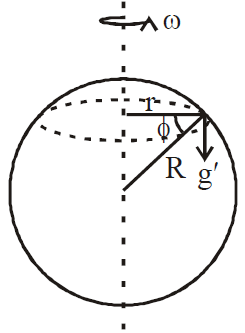
- Due to rotation or latitude of earth
- Due to shape of earth
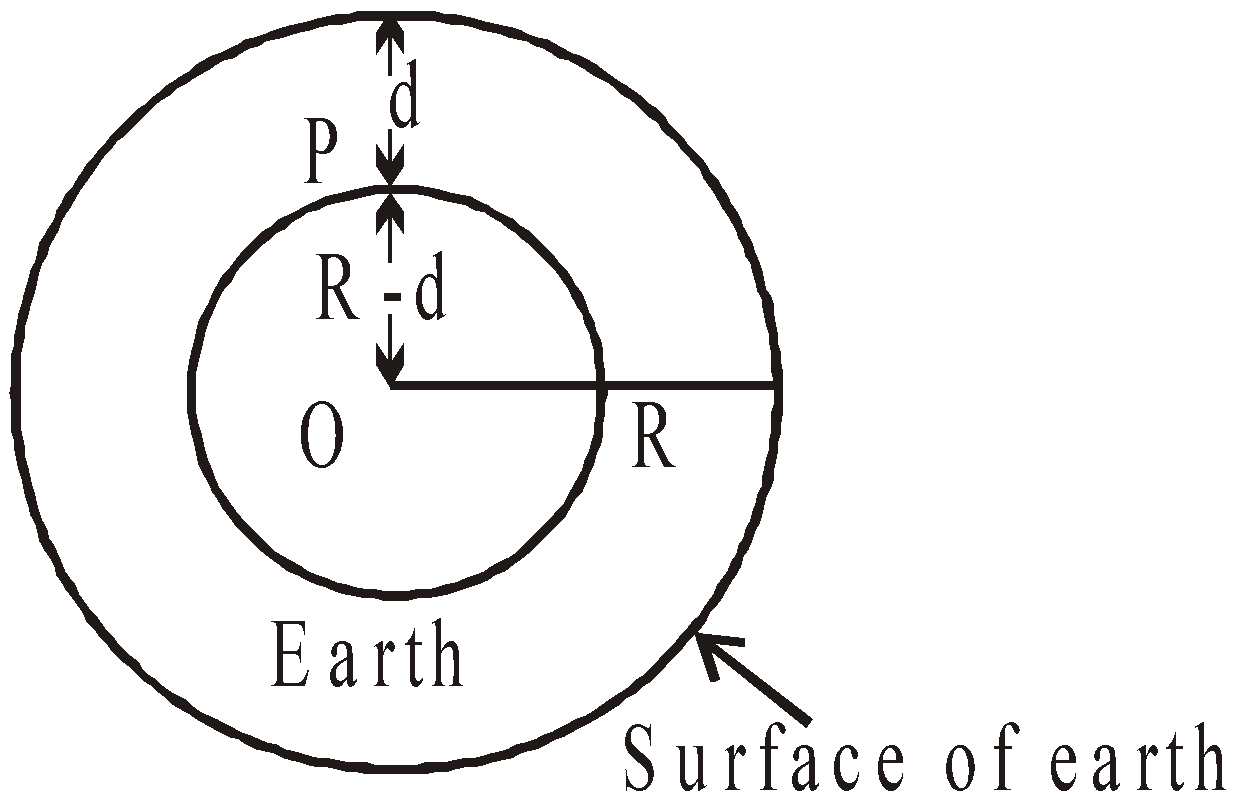
- At a depth ‘d’ below the earth surface
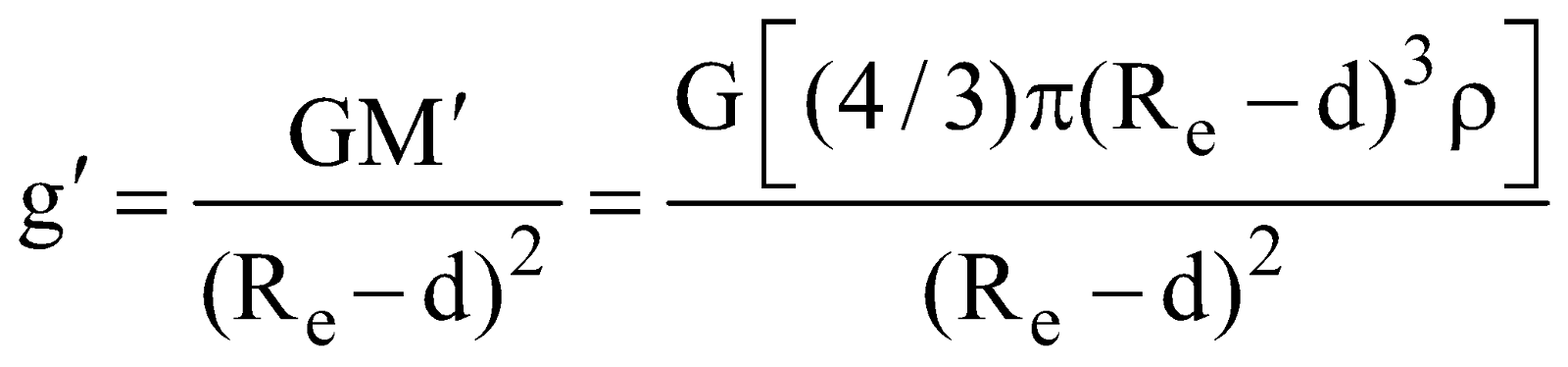
- At a height ‘h’ above the earth surface
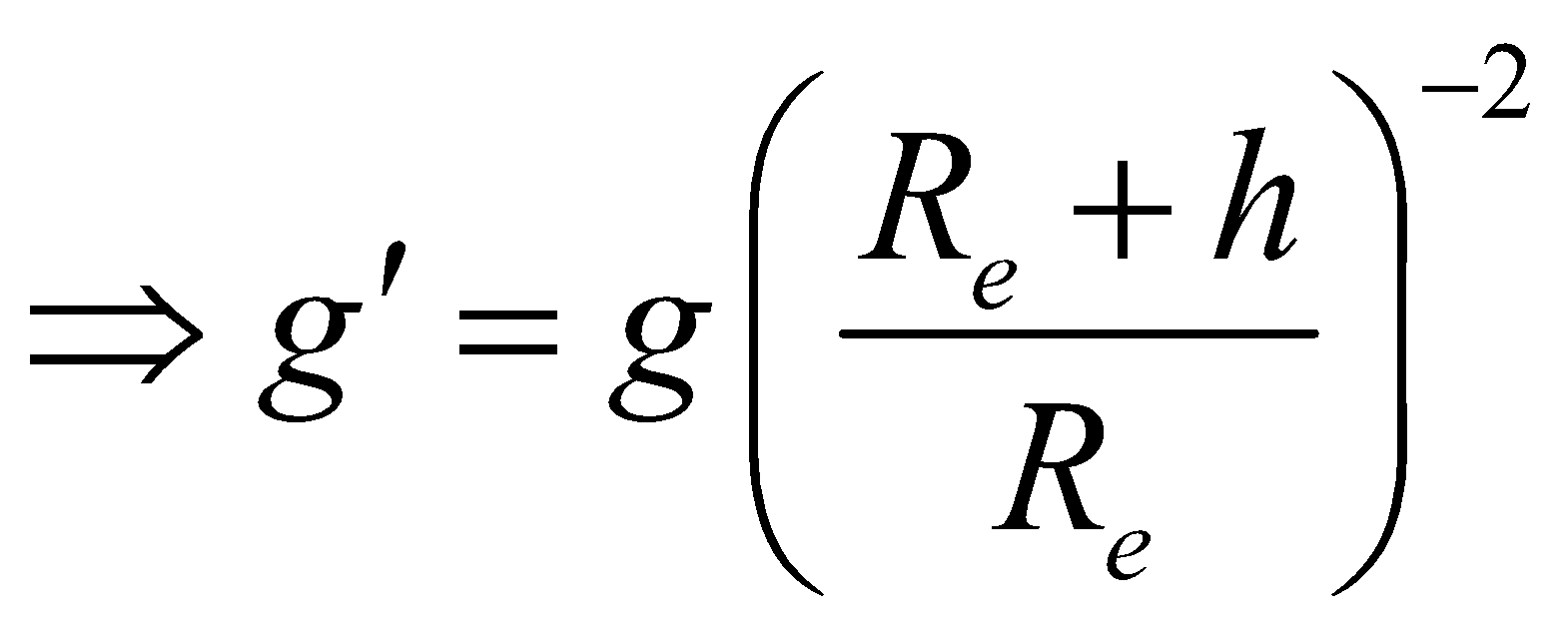 [from eqs. (ix) & (x)]
[from eqs. (ix) & (x)]
- The value of the acceleration due to gravity on the moon is about one sixth of that on the earth and on the sun is about 27 times that on the earth.
- The value of g is minimum on the mercury, among all planets.
- For h<<R, the rate of decrease of the acceleration due to gravity with height is twice as compared to that with depth.
- The value of g increases with the increase in latitude. Its value at latitude θ is given by : gθ= g – Rω2 cos2θ.
- Rotation of the earth about its own axis is responsible for decrease in the value of g with latitude.
- The weight of the body varies along with the value of g (i.e. W = mg)
- Inertial mass and gravitational mass –
- Inertial mass (Mi) defined by Newton’s law of motion
- Gravitational mass Mg defined by Newton’s law of gravitation
- If two spheres of same material, mass and radius are put in contact, the gravitational attraction between them is directly proportional to the fourth power of the radius.
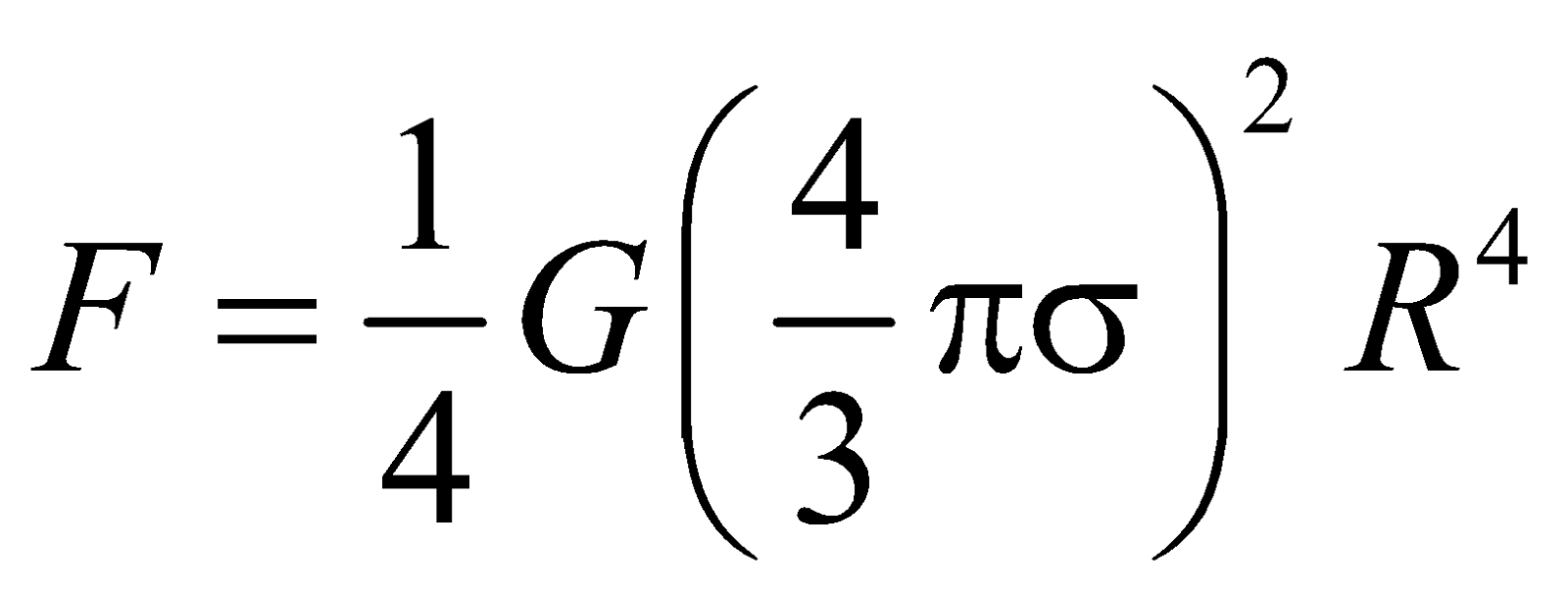
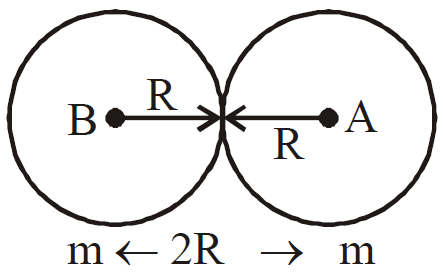
- If the earth stops rotating about its axis, the value of g at the equator will increase by about 0.35%, but that at the poles will remain unchanged.
- If the radius of planet decreases by n%, keeping the mass unchanged, the acceleration due to gravity on its surface increases by 2n%. i.e.,
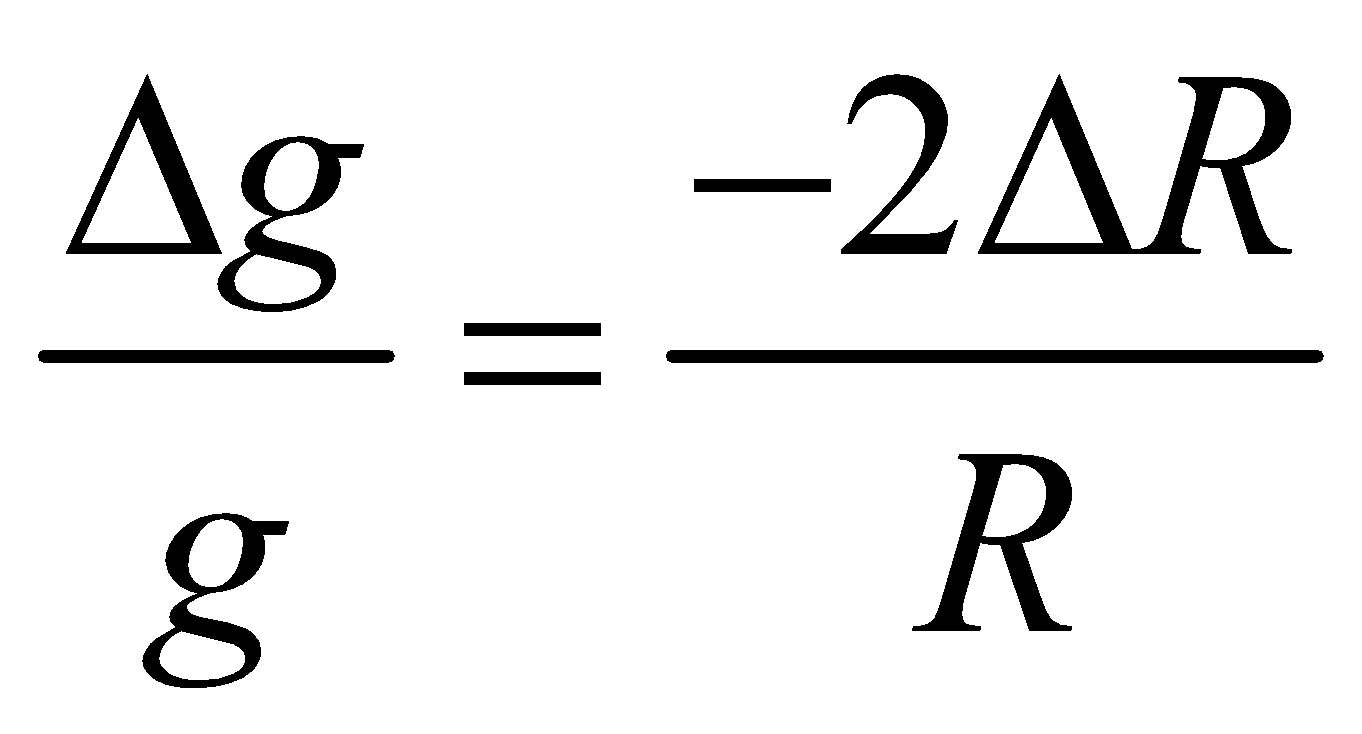
- If the mass of the planet increases by m% keeping the radius constant, the acceleration due to gravity on its surface increases by m% i.e.,
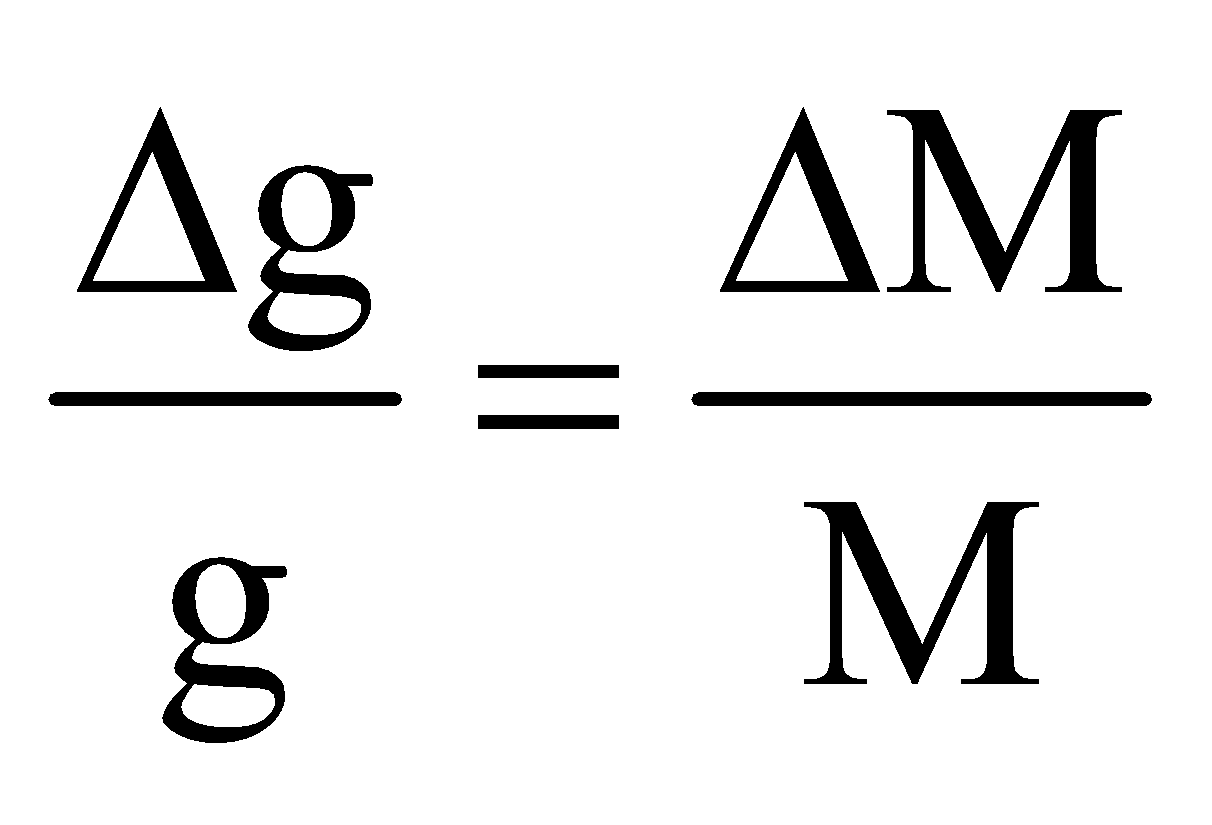 where R = constant.
where R = constant. - If the density of planet decreases by ρ% keeping the radius constant, the acceleration due to gravity decreases by ρ%.
- If the radius of the planet decreases by r% keeping the density constant, the acceleration due to gravity decreases by r%.
GRAVITATIONAL FIELD
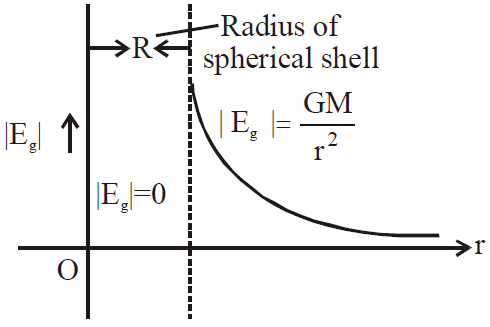
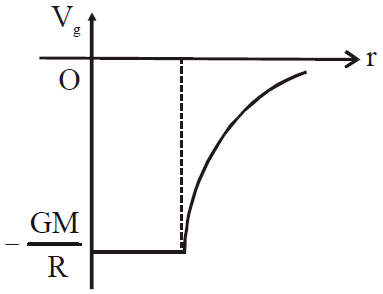
- |Eg|= 0 at points inside the spherical shell (i.e. r < R)
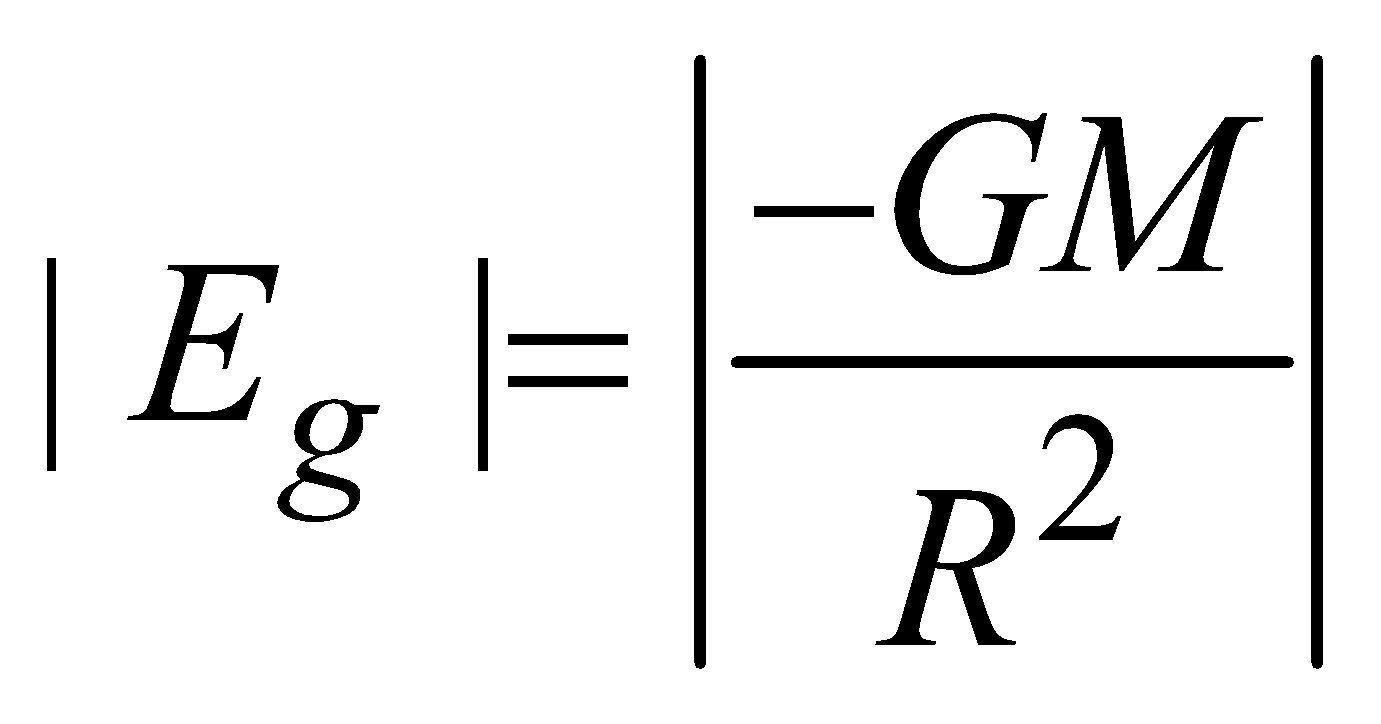 at the surface of shell (i.e. r = R)
at the surface of shell (i.e. r = R)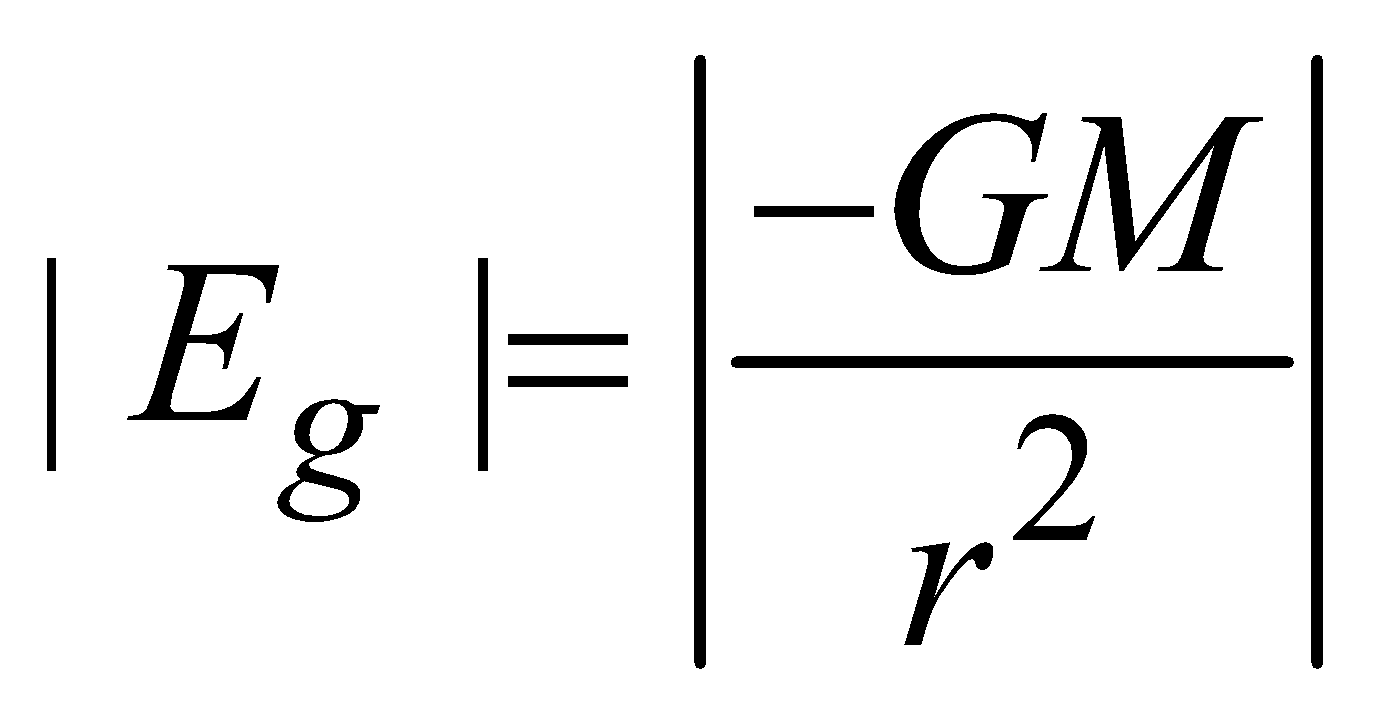 for outside the spherical shell (r >R)
for outside the spherical shell (r >R)
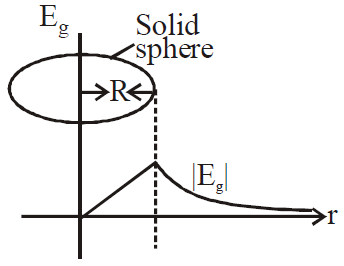
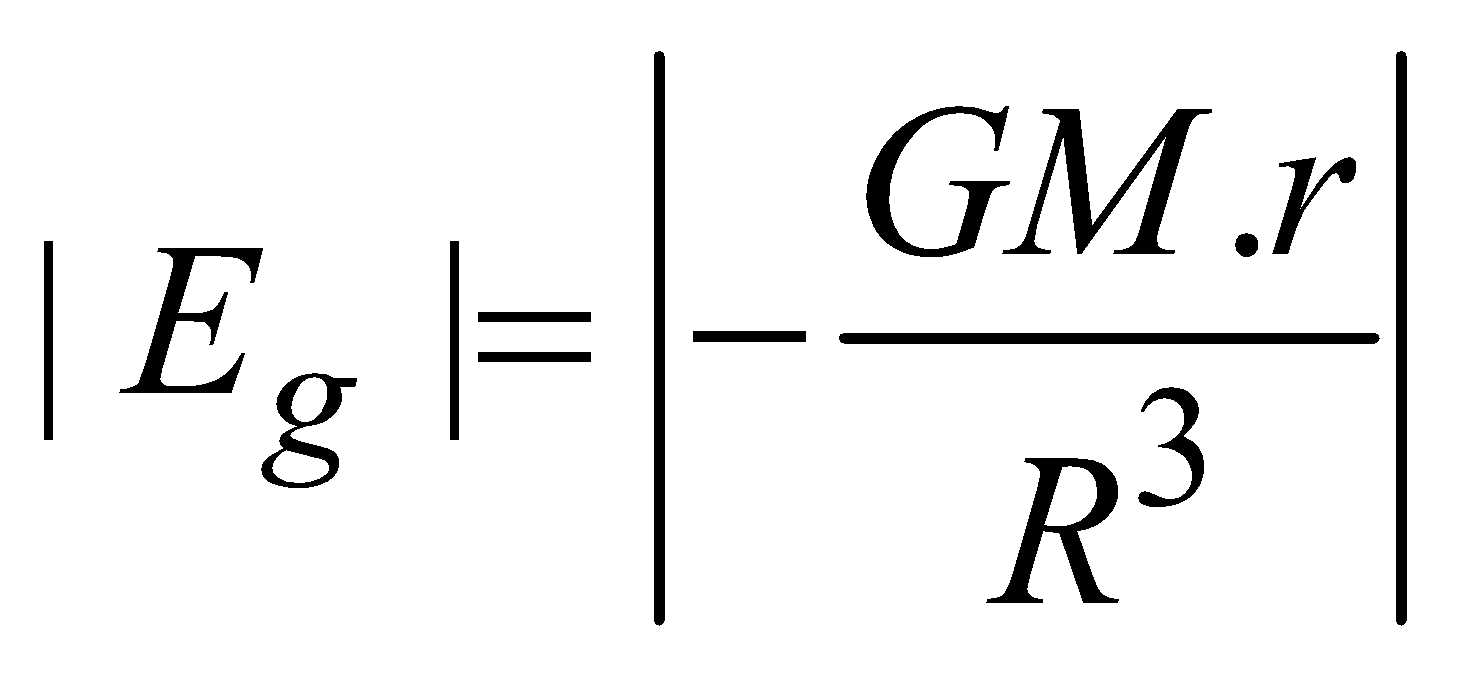 for points inside the solid sphere (r<R)
for points inside the solid sphere (r<R) 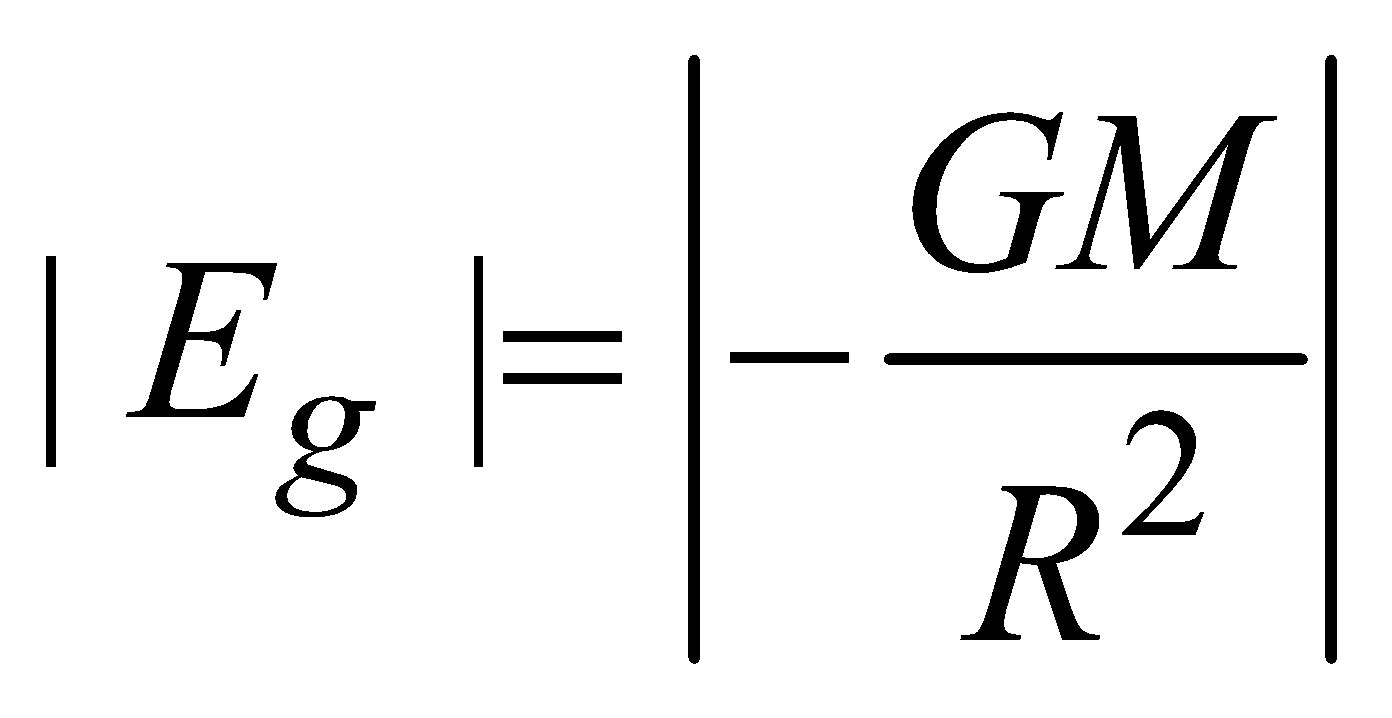 At the surface of solid sphere (r = R)
At the surface of solid sphere (r = R) 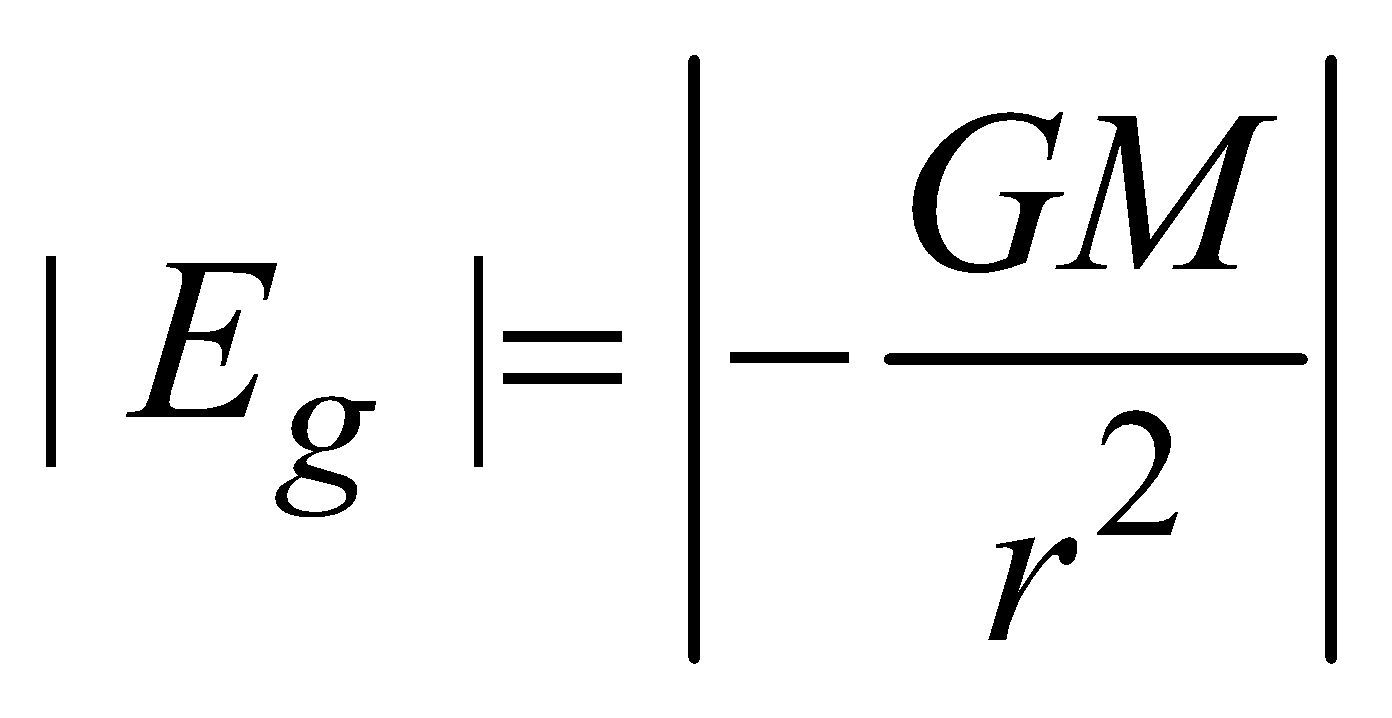 Outside the solid sphere (r > R)
Outside the solid sphere (r > R)
GRAVITATIONAL POTENTIAL
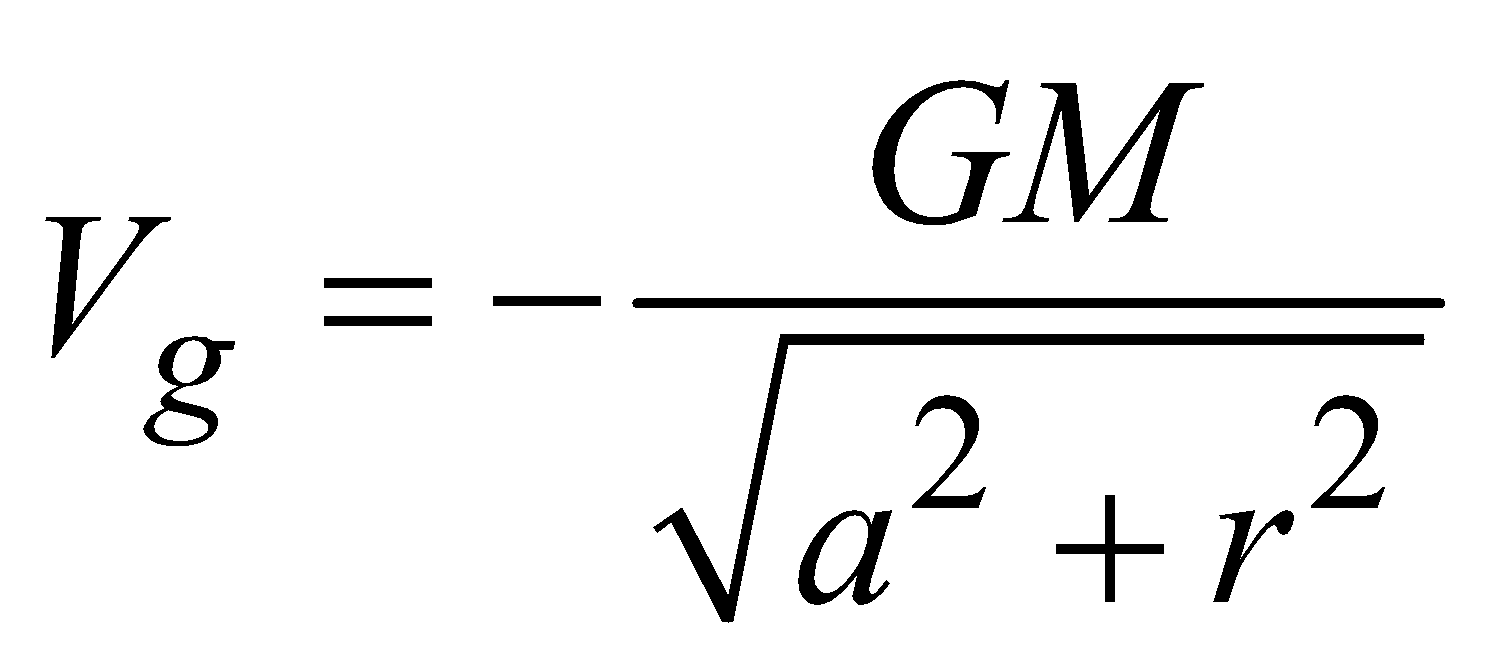
- at a point outside the shell,
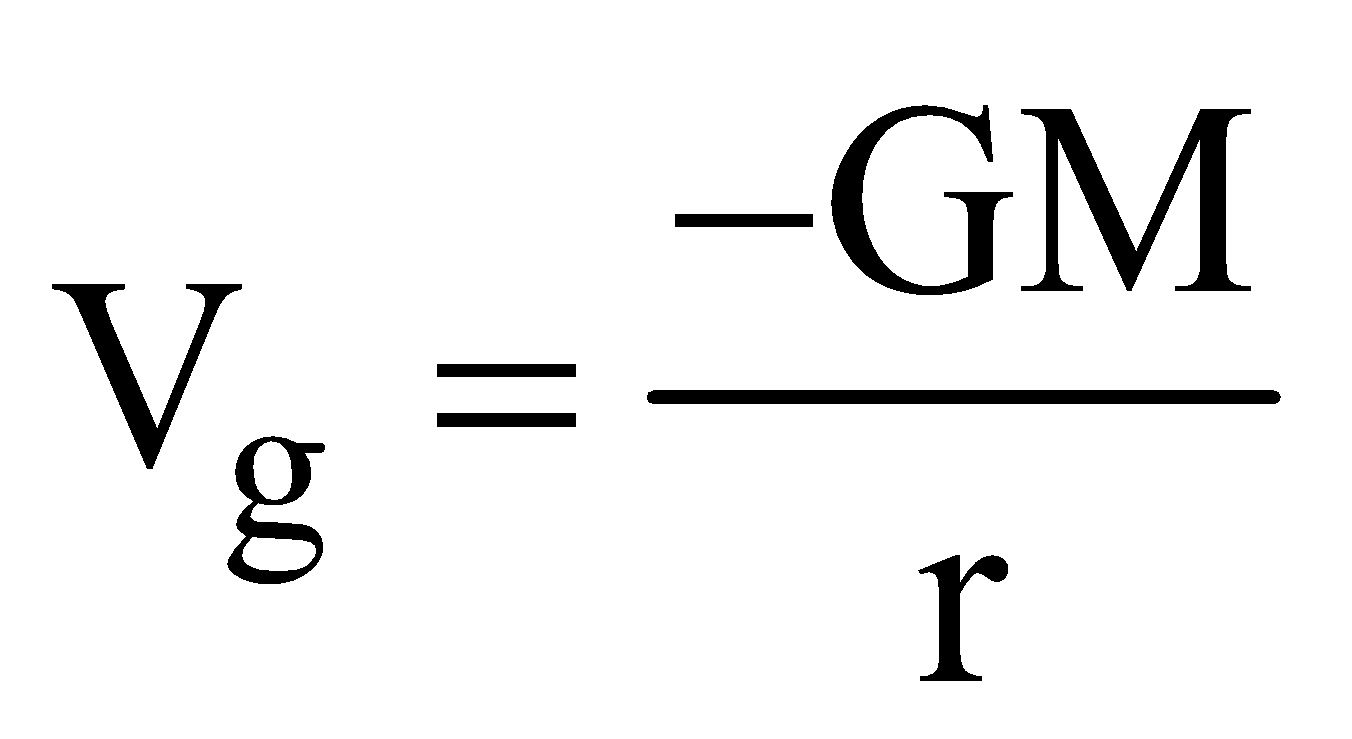 (r > R)
(r > R) - at a point inside the shell,
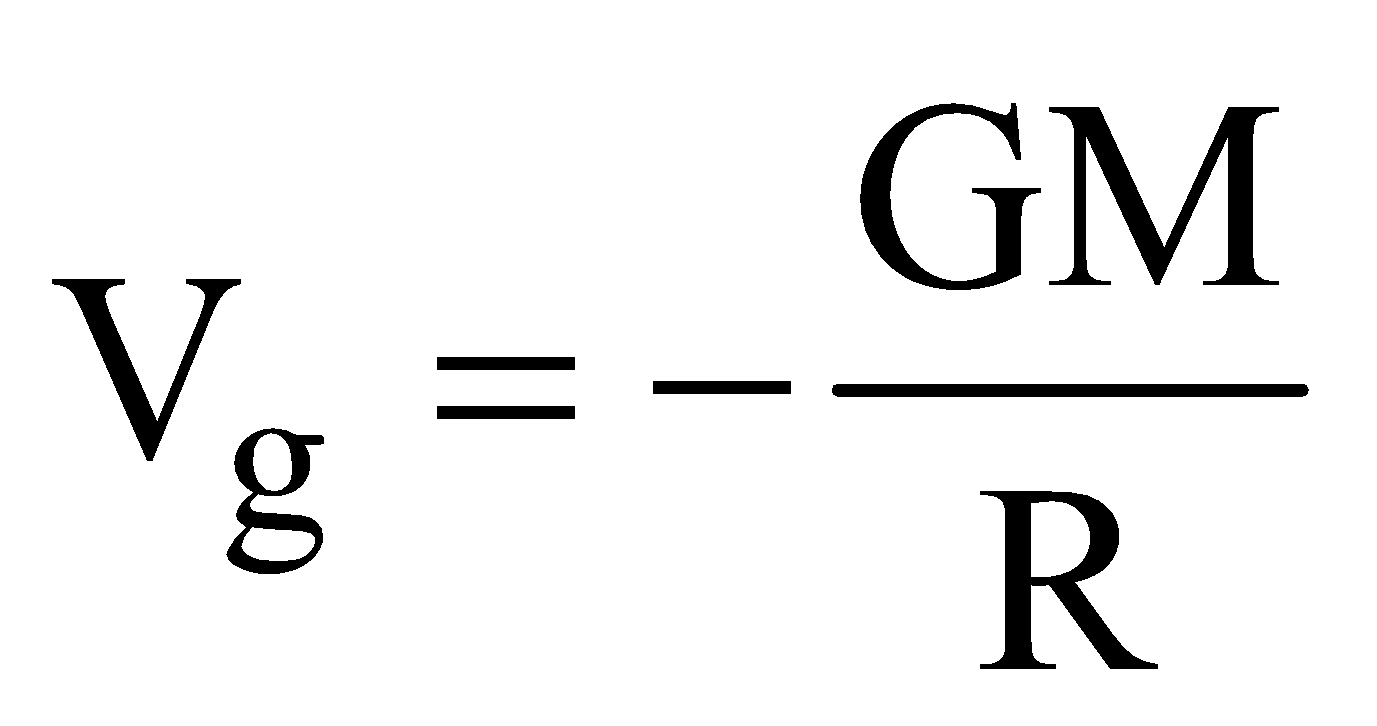 (r < R)
(r < R)
- at an external point
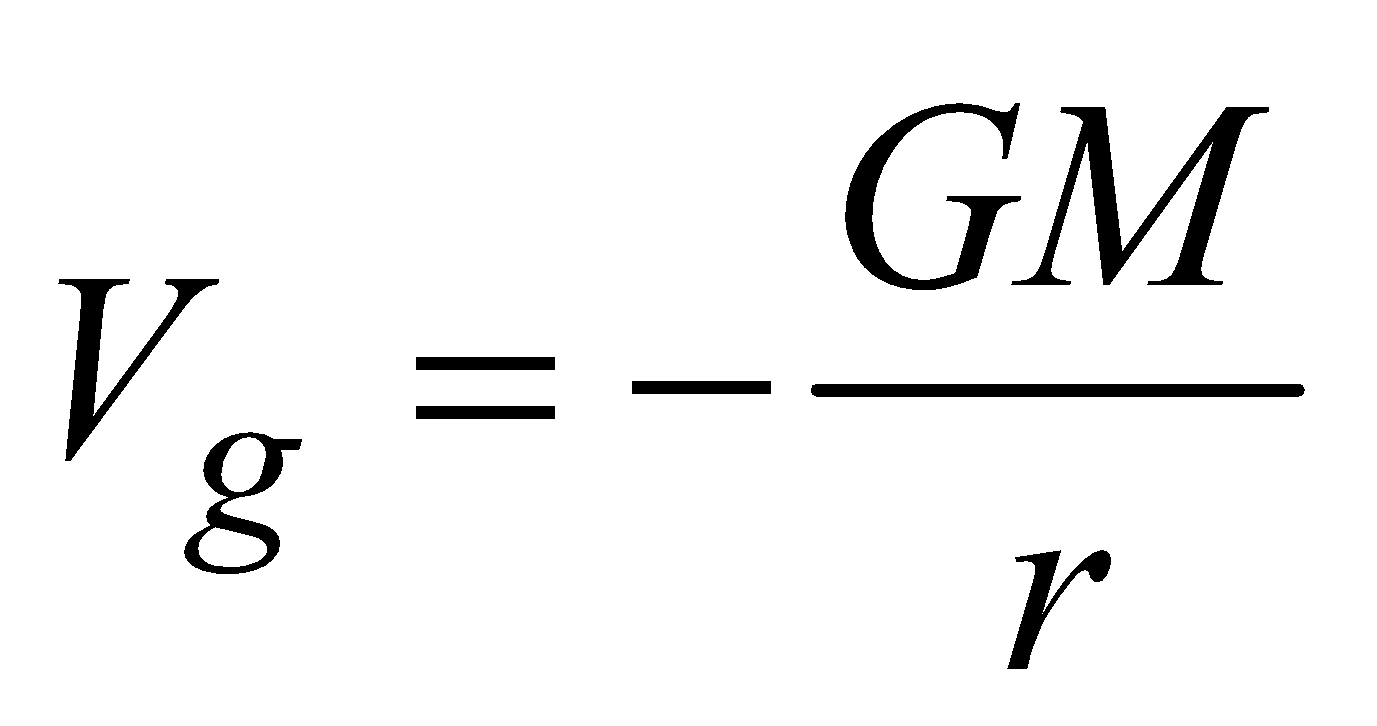 (r≥ R)
(r≥ R)
- at an internal point
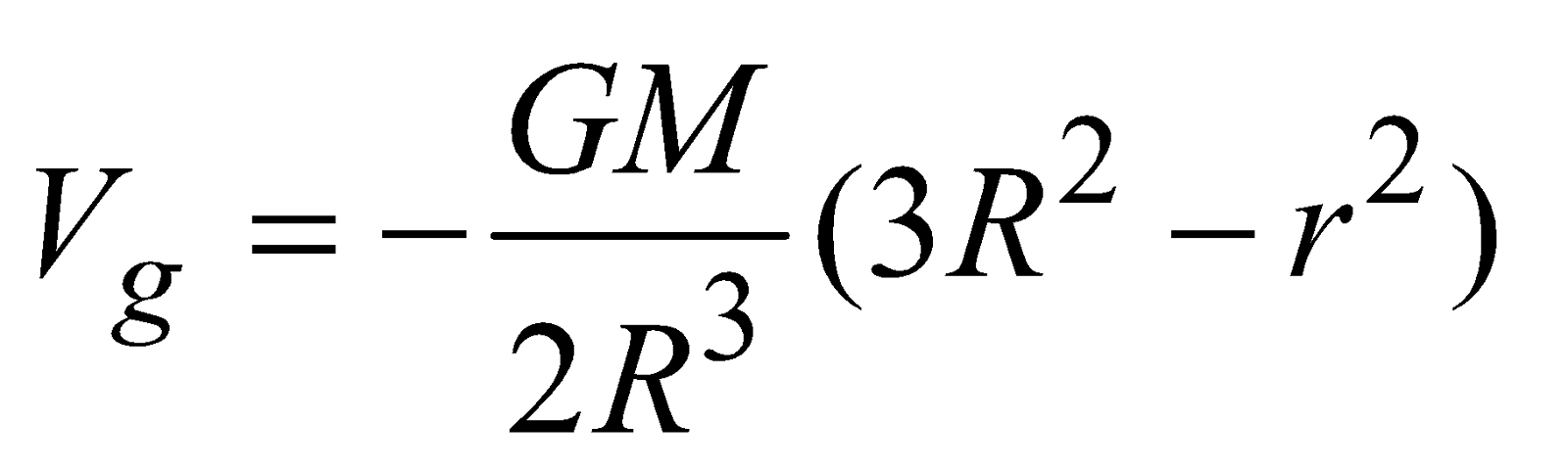 (r < R)
(r < R)
- Potential at the centre of solid sphere is
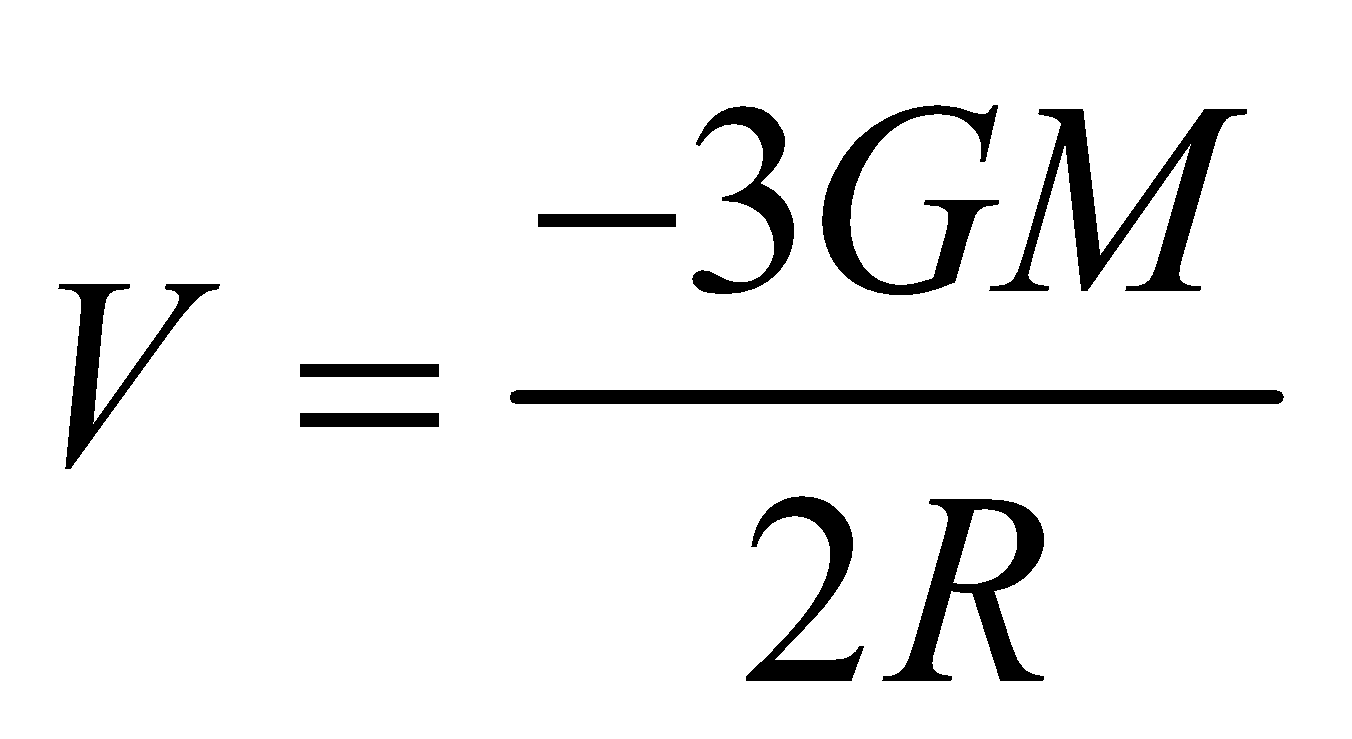
GRAVITATIONAL POTENTIAL ENERGY
- The gravitational potential energy of a mass m at a point above the surface of the earth at a height h is given by
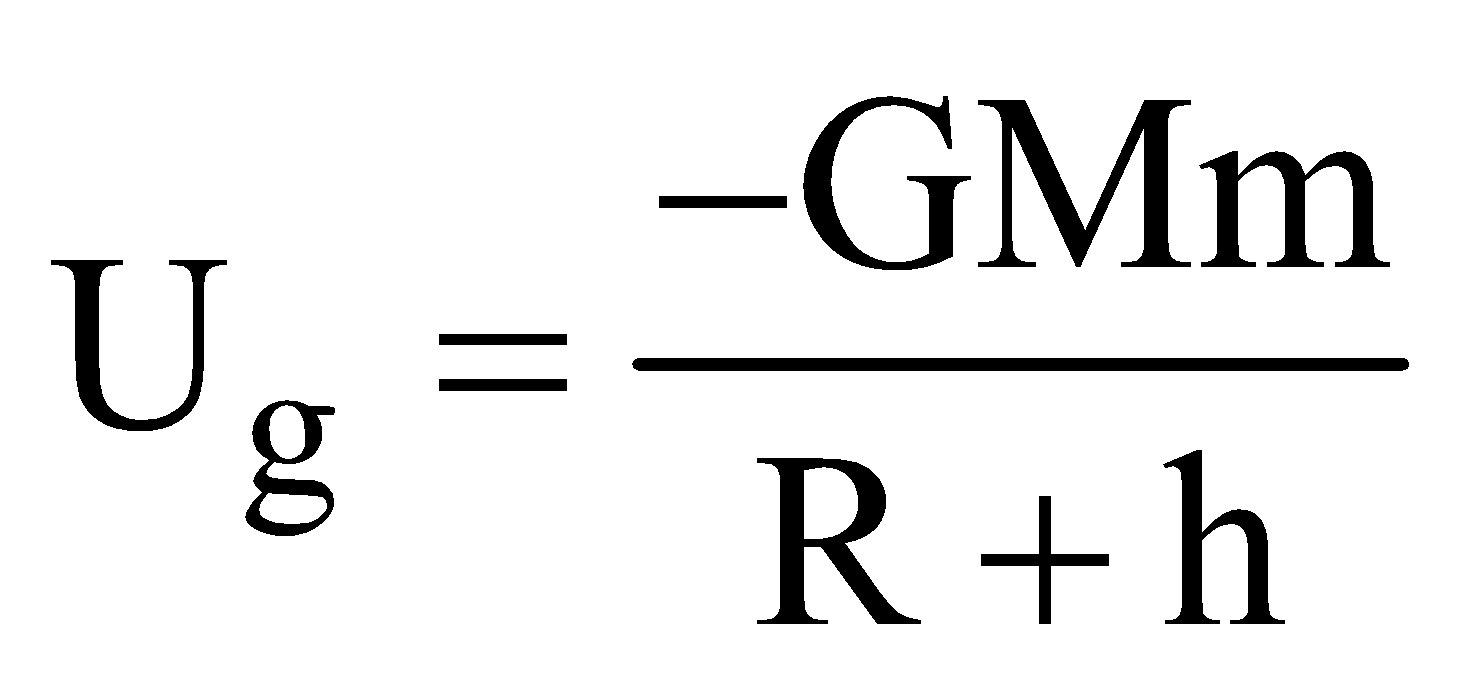 . The –ve sign shows that if h increases, the gravitational PE decreases and becomes zero at infinity.
. The –ve sign shows that if h increases, the gravitational PE decreases and becomes zero at infinity. - If we take reference level to be at the surface of earth (not at infinity) i.e., we assume that the gravitational P.E of a mass m is zero at the surface of earth, then the gravitational potential energy at a height h above the surface of earth is (mgh), where h << Re (radius of earth)
- The gravitational P.E of mass m on the earth’s surface is
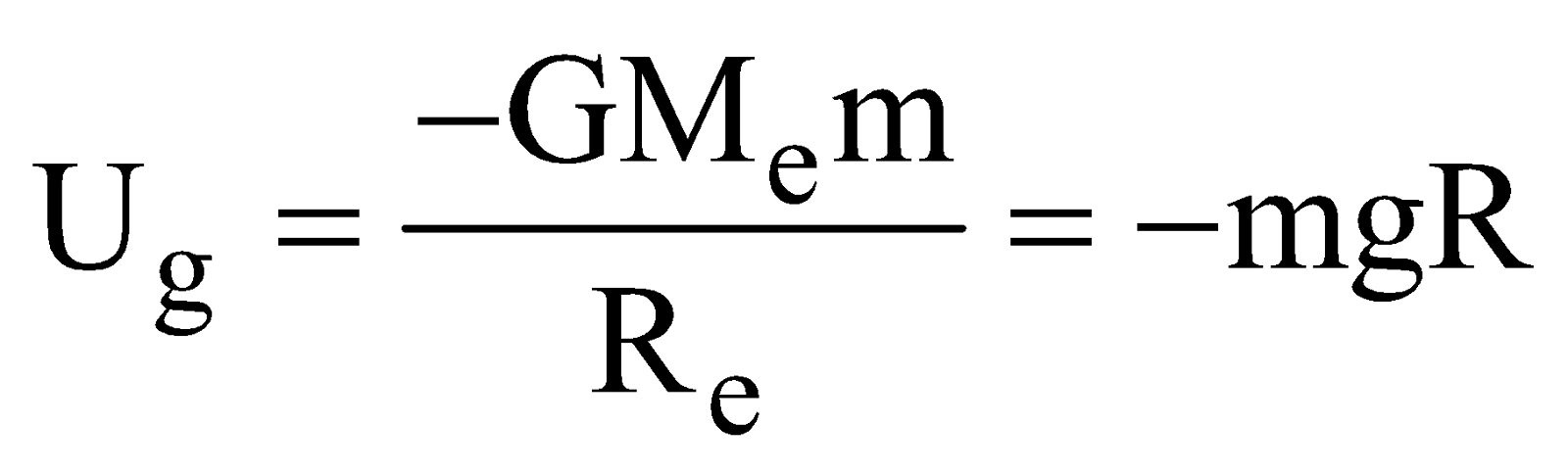
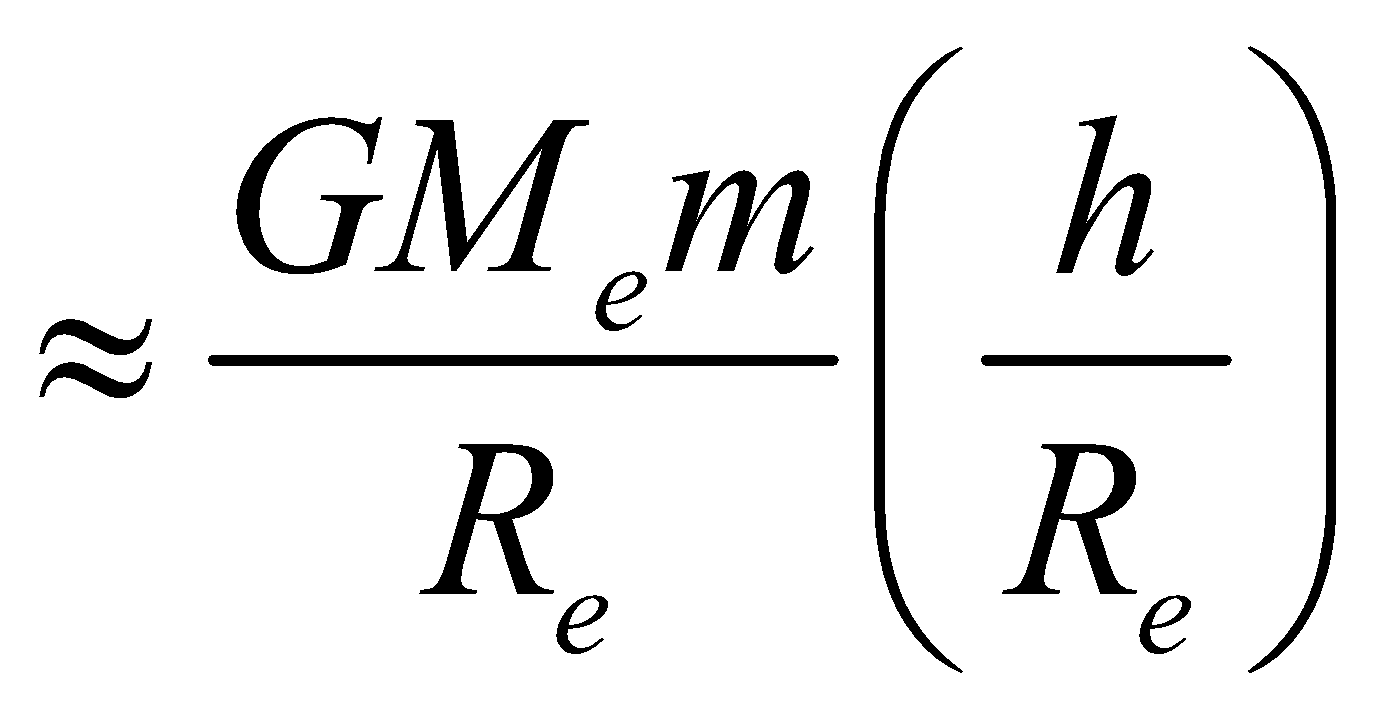 (if h<<R)
(if h<<R)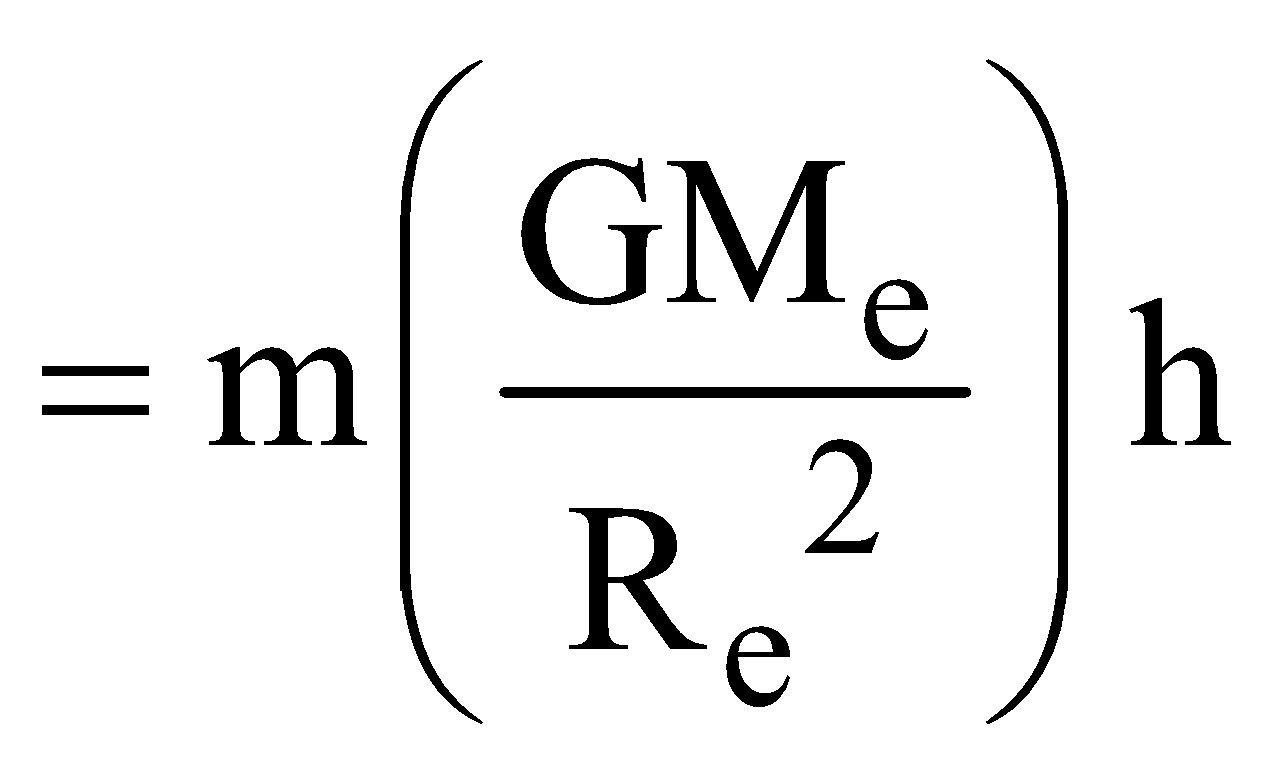
SATELLITES
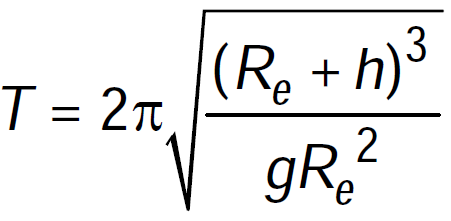
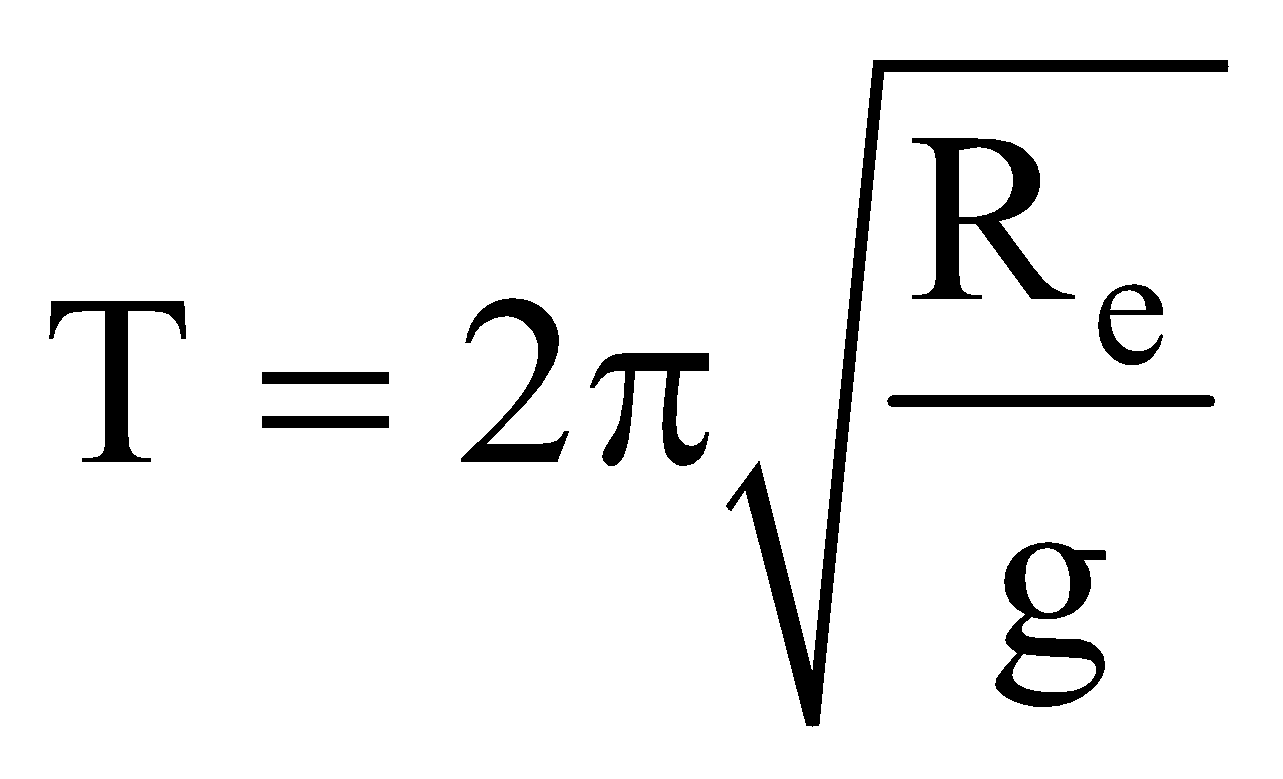 ; Re = 6.4 × 106 m ; g = 9.8 ms–2
; Re = 6.4 × 106 m ; g = 9.8 ms–2ORBITAL VELOCITY (V0 )
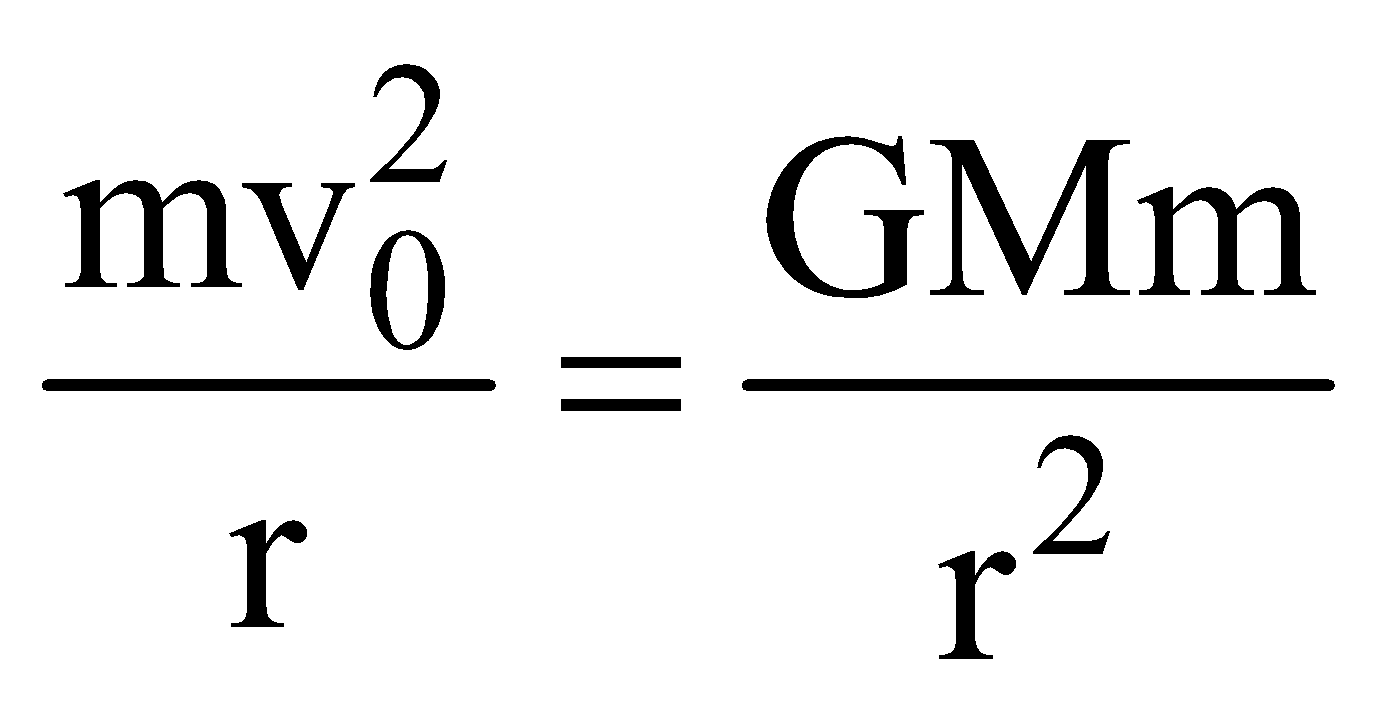 or
or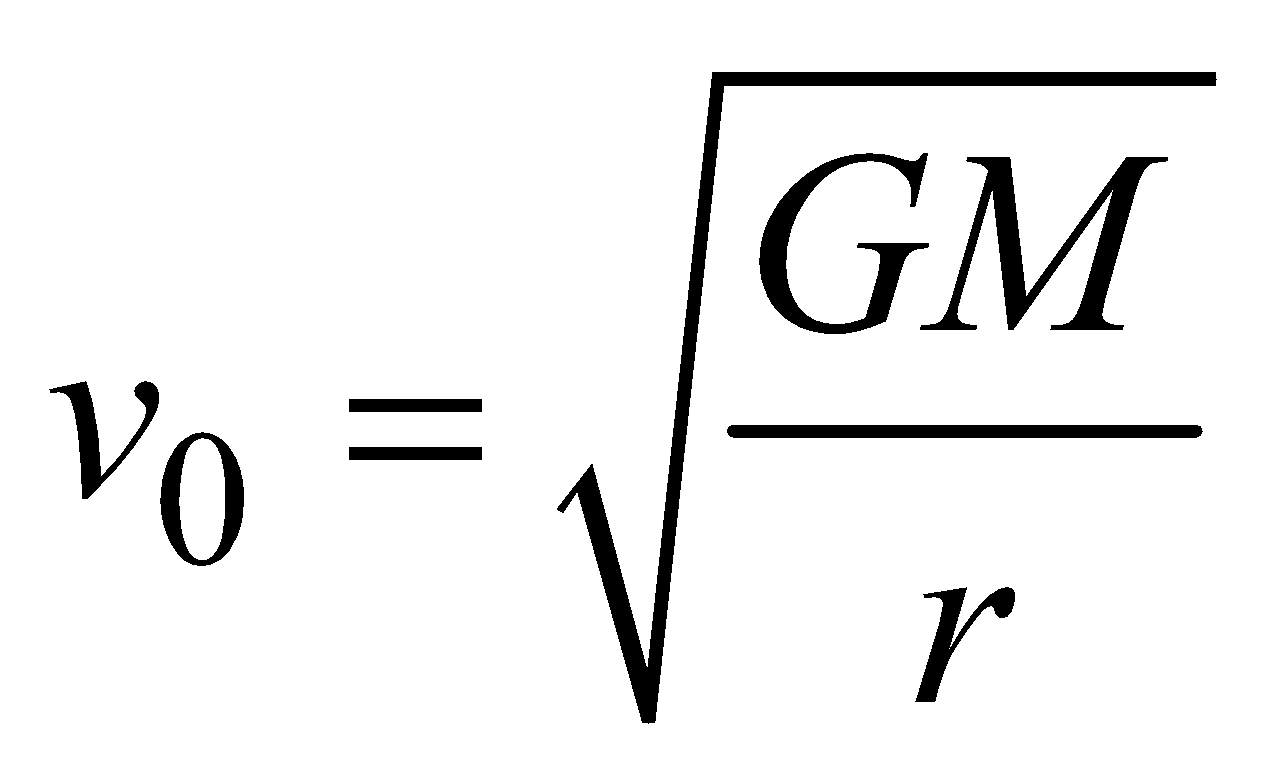 ………. (1)
………. (1)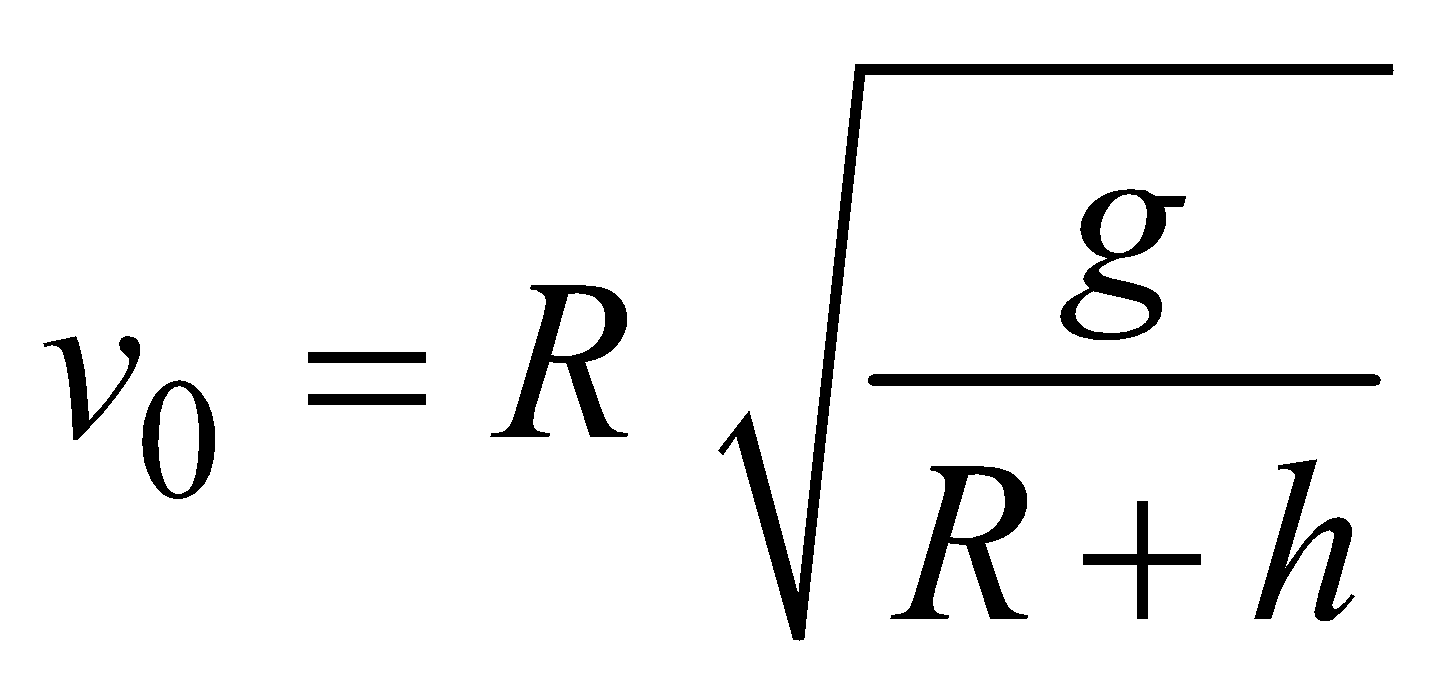 [∵
[∵ 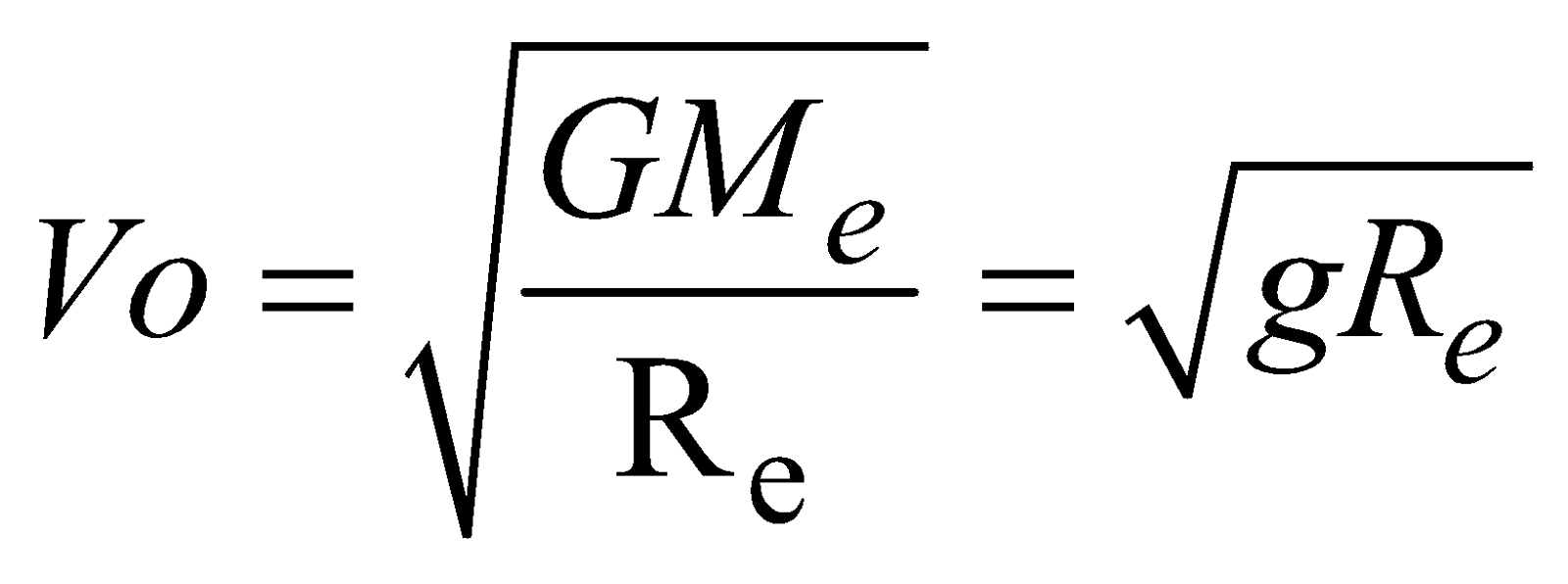
- Value of orbital velocity does not depend on the mass of the satellite.
- Around the earth the value of orbital velocity is 7.92 km/sec.
- Greater is the height of the satellite, smaller is the orbital velocity.
- The direction of orbital velocity is along the tangent to the path.
- The work done by the satellite in a complete orbit is zero.
ANGULAR MOMENTUM (L)
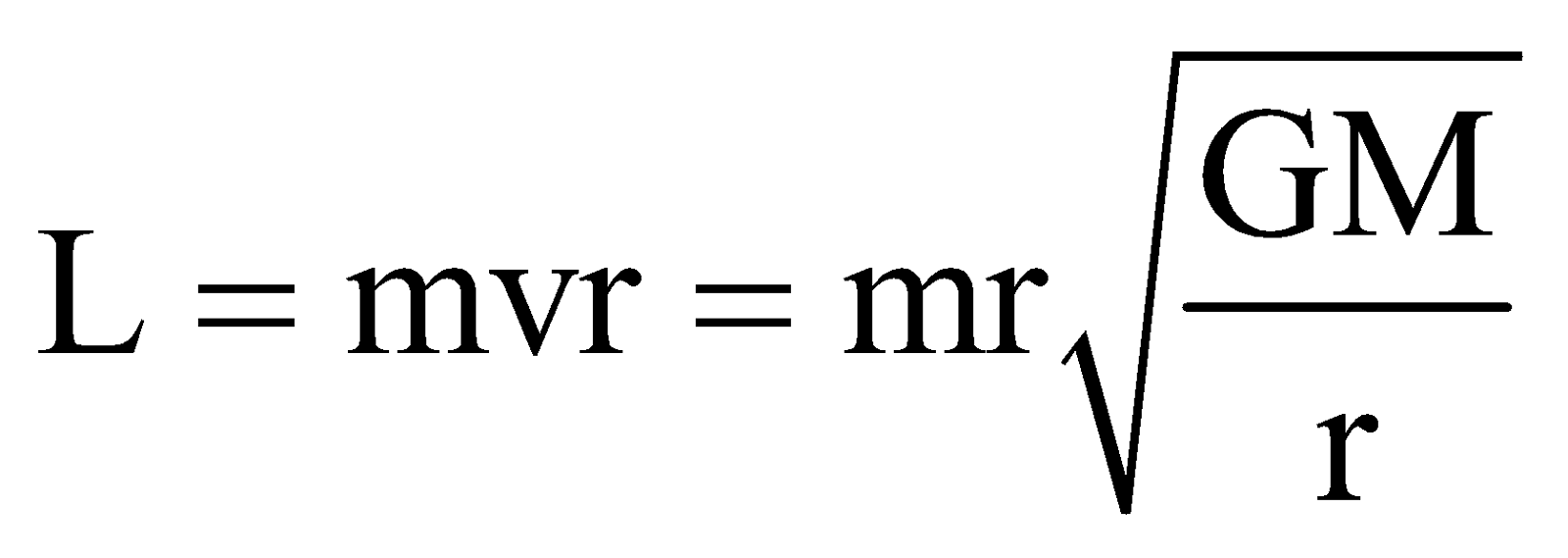
ENERGY OF A SATELLITE
- The gravitational potential energy of a satellite of mass m
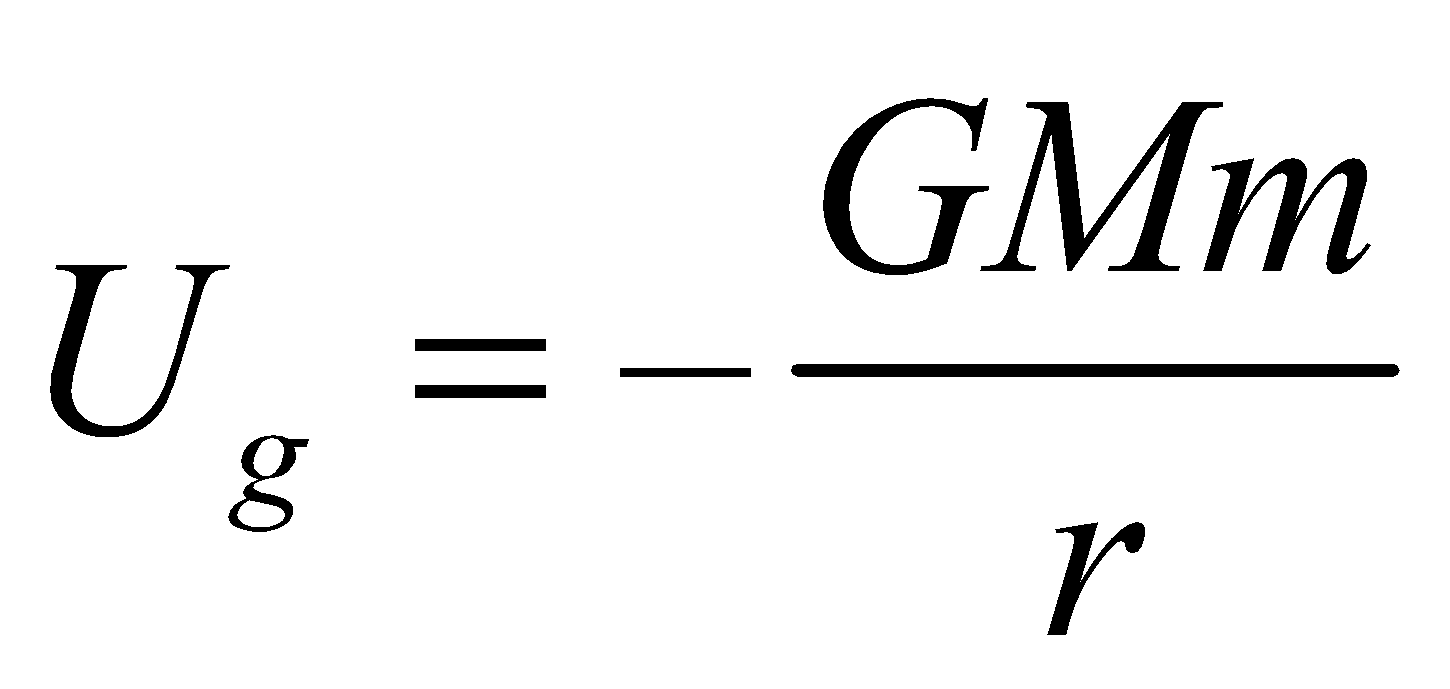 , where r is the radius of the orbit.
, where r is the radius of the orbit. - Kinetic energy of the satellite
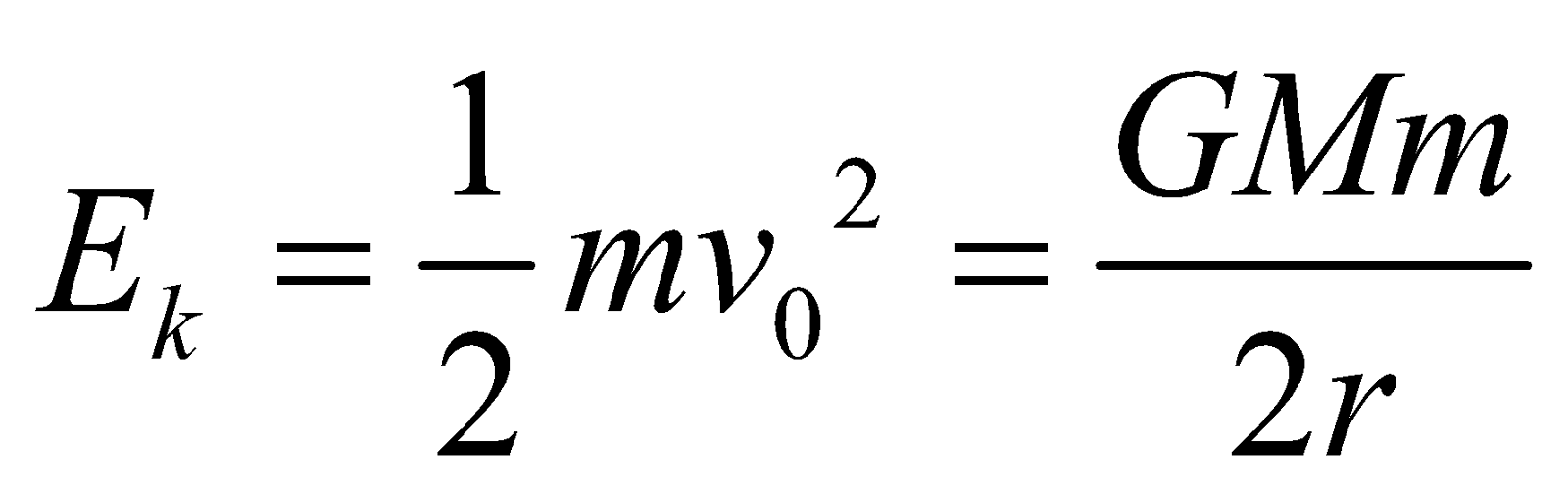
- So, total energy of the satellite
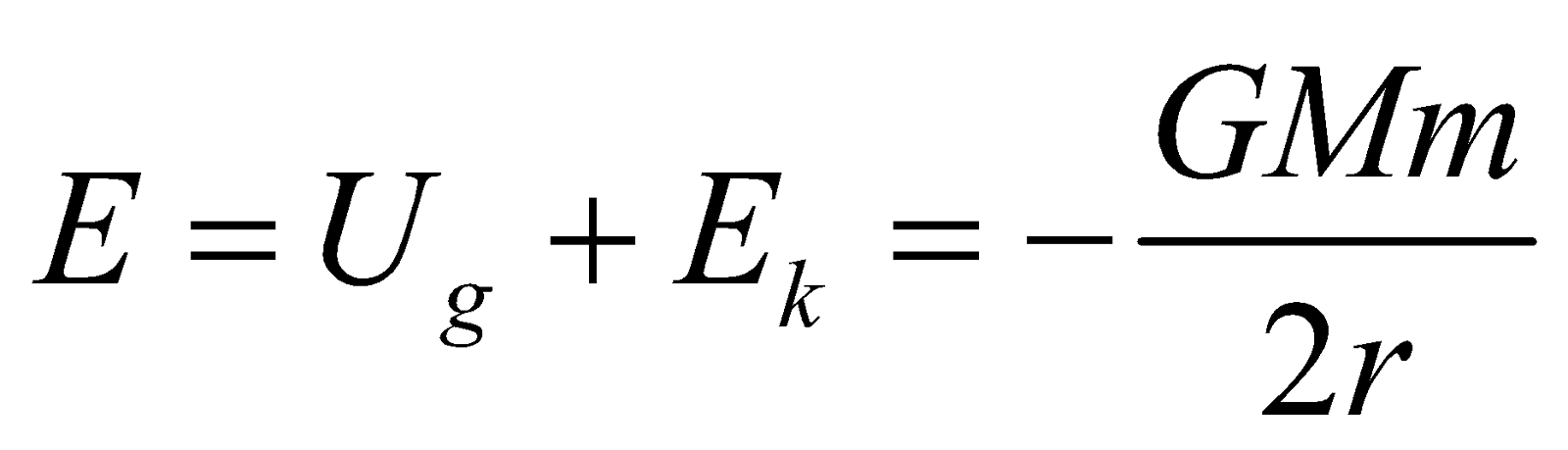
- Total energy of a satellite at a height equal to the radius of the earth
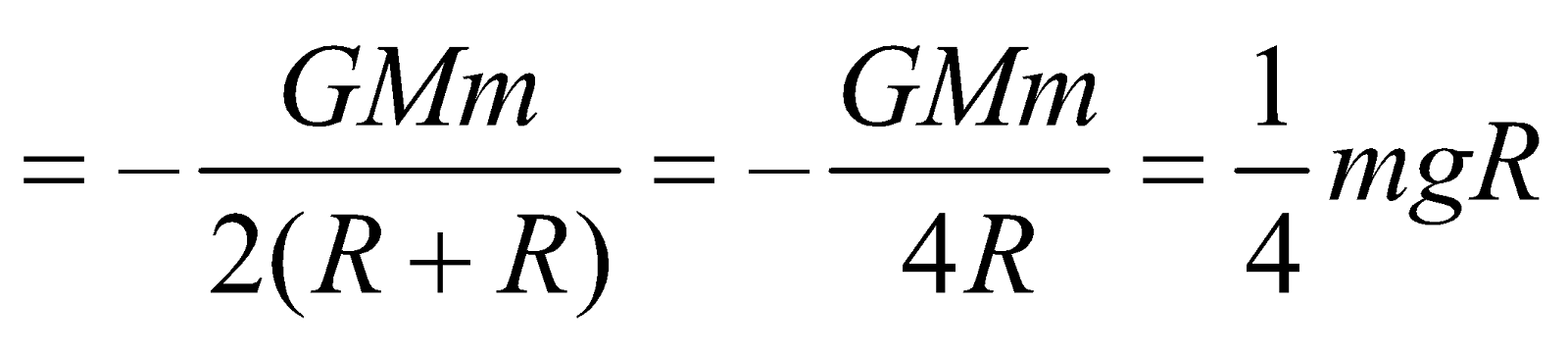
GEO-STATIONARY SATELLITE
- The orbit of the satellite must be circular and in the equatorial plane of the earth.
- The angular velocity of the satellite must be in the same direction as the angular velocity of rotation of the earth i.e., from west to east.
- The period of revolution of the satellite must be equal to the period of rotation of earth about its axis. i.e. 24 hours = 24 × 60 × 60 = 86400 sec.
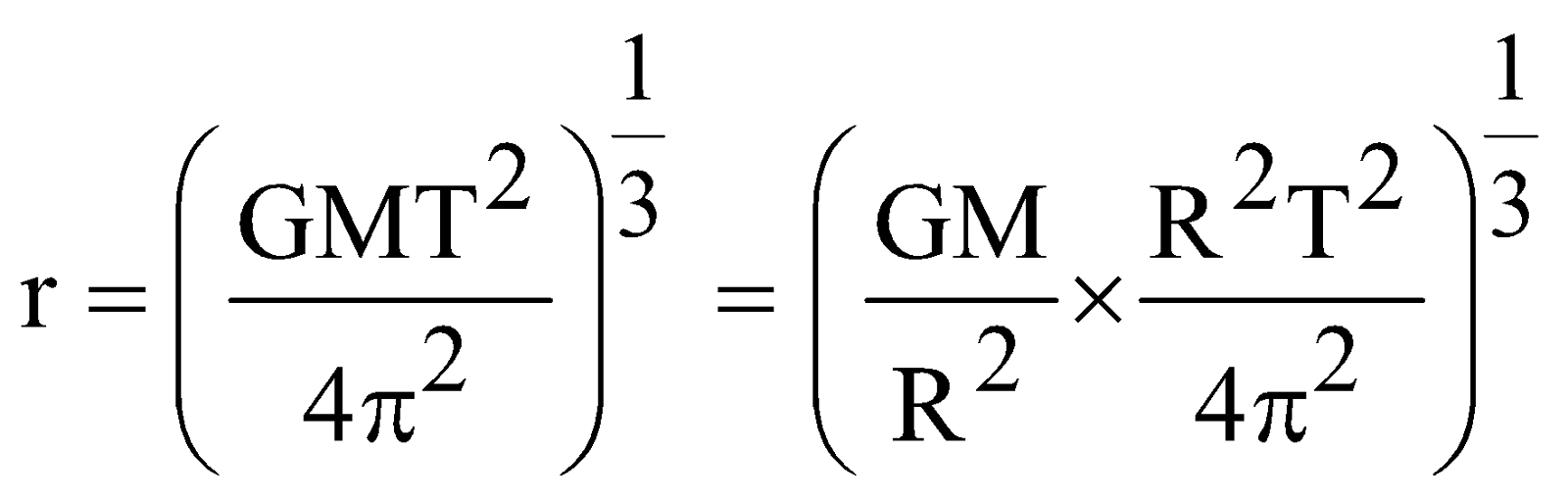
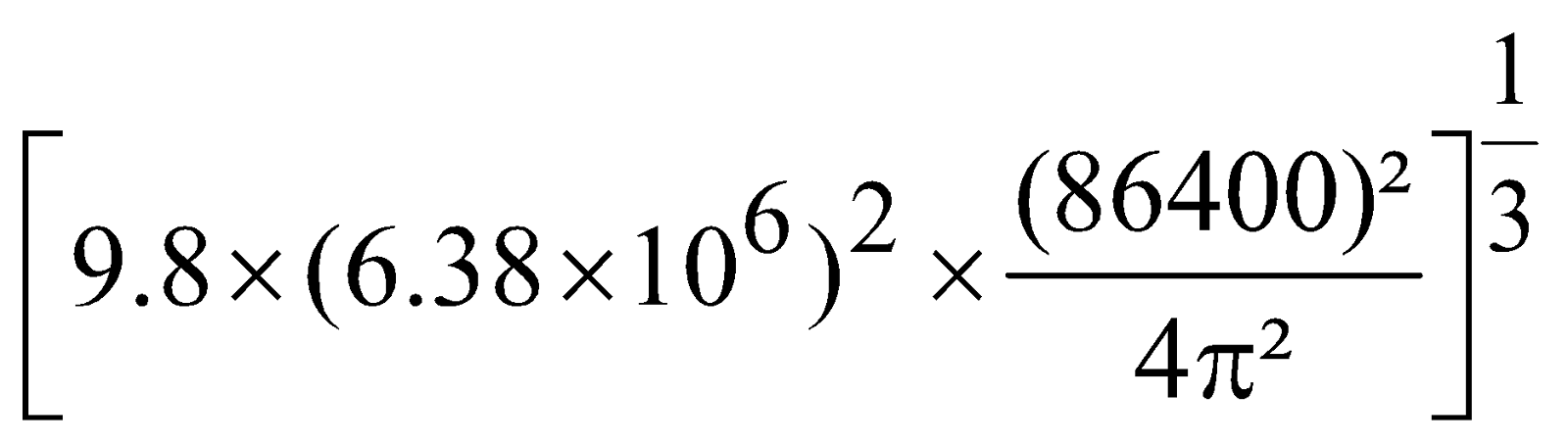
- Height of geostationary satellite from the surface of the earth is nearly 35600 km.
- The orbital velocity of this satellite is nearly 3.08 km/sec.
- The relative velocity of geostationary satellite with respect to earth is zero.
- This type of satellite is used for communication purposes. The orbit of a geostationary satellite is called ‘Parking Orbit’.
POLAR SATELLITE
- When v < v0
- The path is spiral. The satellite finally falls on the earth
- Kinetic energy is less than potential energy
- Total energy is negative
- When v = v0
- The path is circular
- Eccentricity is zero
- Kinetic energy is less than potential energy
- Total energy is negative
- When v0 < v < ve
- The path is elliptical
- Eccentricity < 1
- Kinetic energy is less than potential energy
- Total energy is negative
- When v = ve
- The path is a parabola
- Eccentricity = 1
- Kinetic energy is equal to potential energy
- Total energy is zero
- When v > ve
- The path is a hyperbola
- Eccentricity > 1
- Kinetic energy is greater than potential energy
- Total energy is positive
- The energy
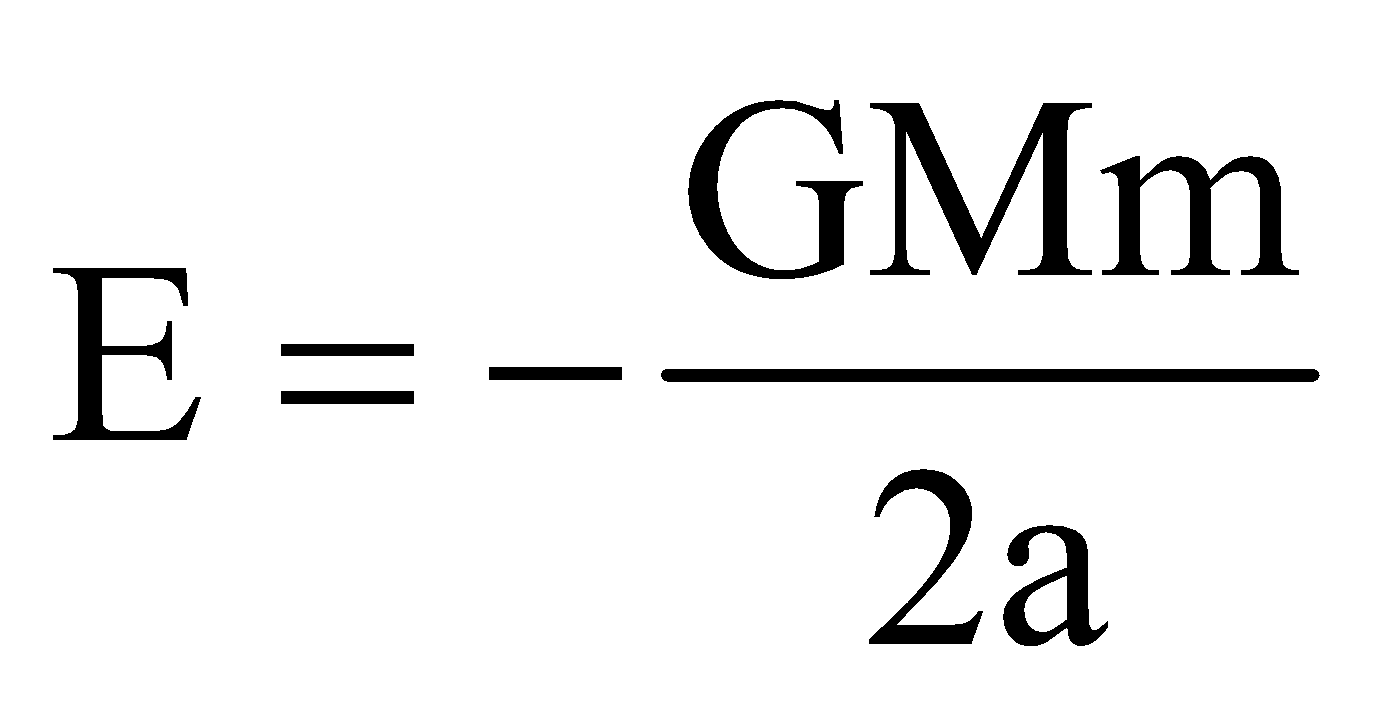 = const. with ‘a’ as semi-major axis;
= const. with ‘a’ as semi-major axis; - KE will be maximum when the satellite is closest to the central body (at perigee) and minimum when it is farthest from the central body (at apogee) [as for a given orbit L = const.,
i.e., mvr = const., i.e., v ∝ 1/r] - PE = (E – KE) will be minimum when KE = max, i.e., the satellite is closest to the central body (at perigee) and maximum when KE = min, i.e., the satellite is farthest from the central body (at apogee).
ESCAPE SPEED (Ve)
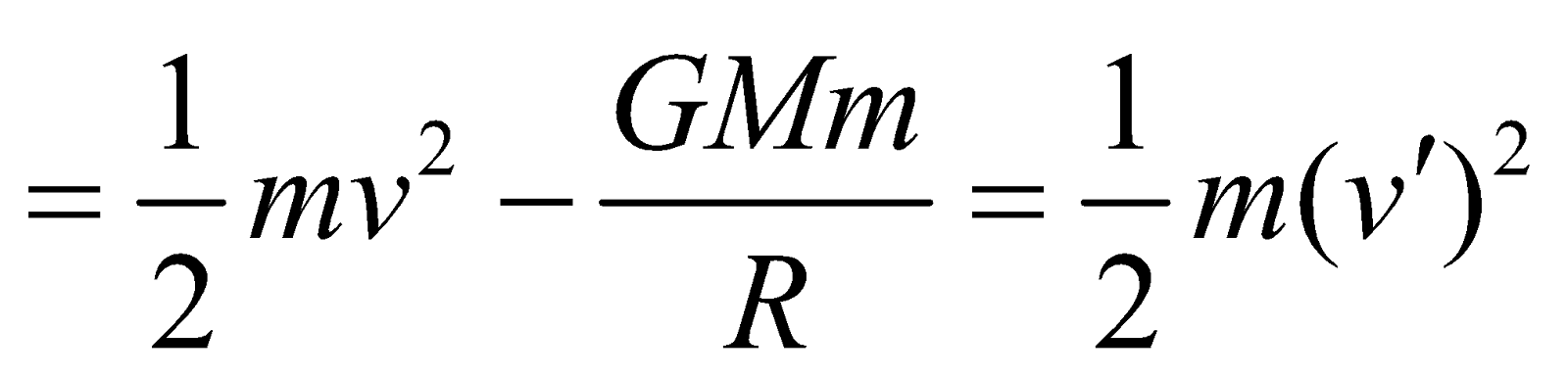
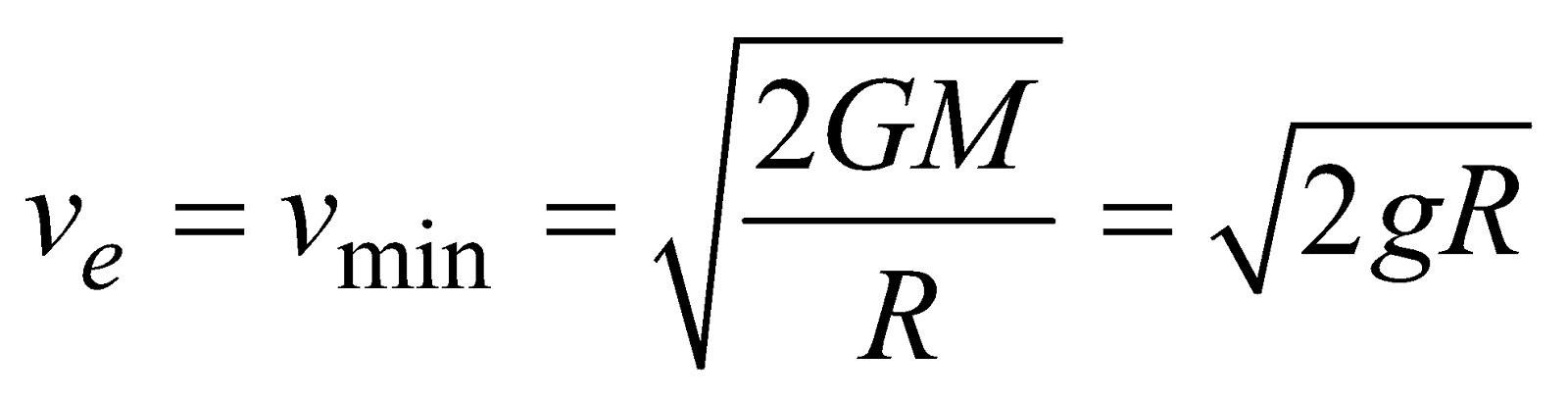
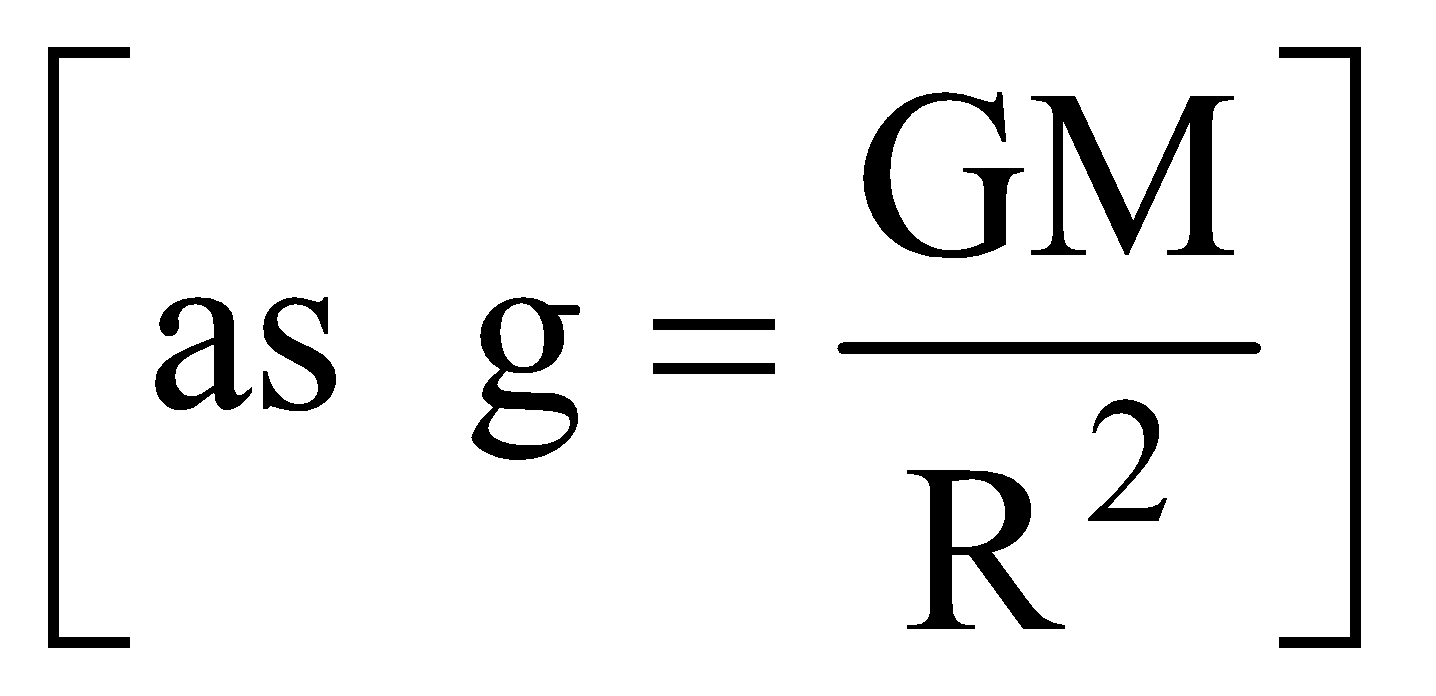
- The value of escape velocity does not depend upon the mass of the projected body, instead it depends on the mass and radius of the planet from which it is being projected.
- The value of escape velocity does not depend on the angle and direction of projection.
- The value of escape velocity from the surface of the earth is 11.2 km/sec.
- The minimum energy needed for escape is = GMm/R.
- If the velocity of a satellite orbiting near the surface of the earth is increased by 41.4%, then it will escape away from the gravitational field of the earth.
- If a body falls freely from infinite distance, then it will reach the surface of earth with a velocity of 11.2 km/sec.
- The escape velocity on moon is low as (as gm=gE/6) hence there is no atmosphere on moon.
- If the orbital radius of the earth around the sun be one fourth of the present value, then the duration of the year will be one eighth of the present value.
- The satellites revolve around the earth in a plane that coincides with the great circle around the earth.
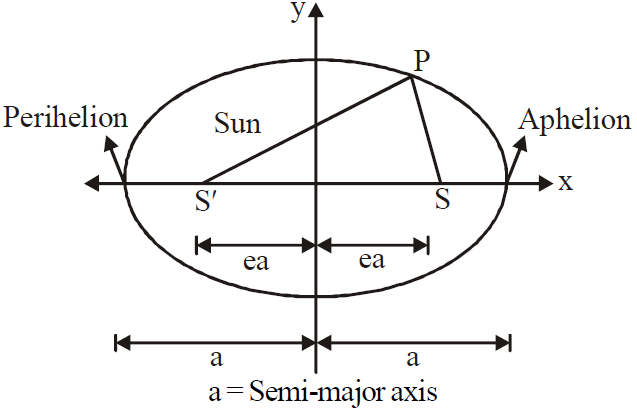
KEPLER’S LAWS OF PLANETARY MOTION
LAW OF ORBITS
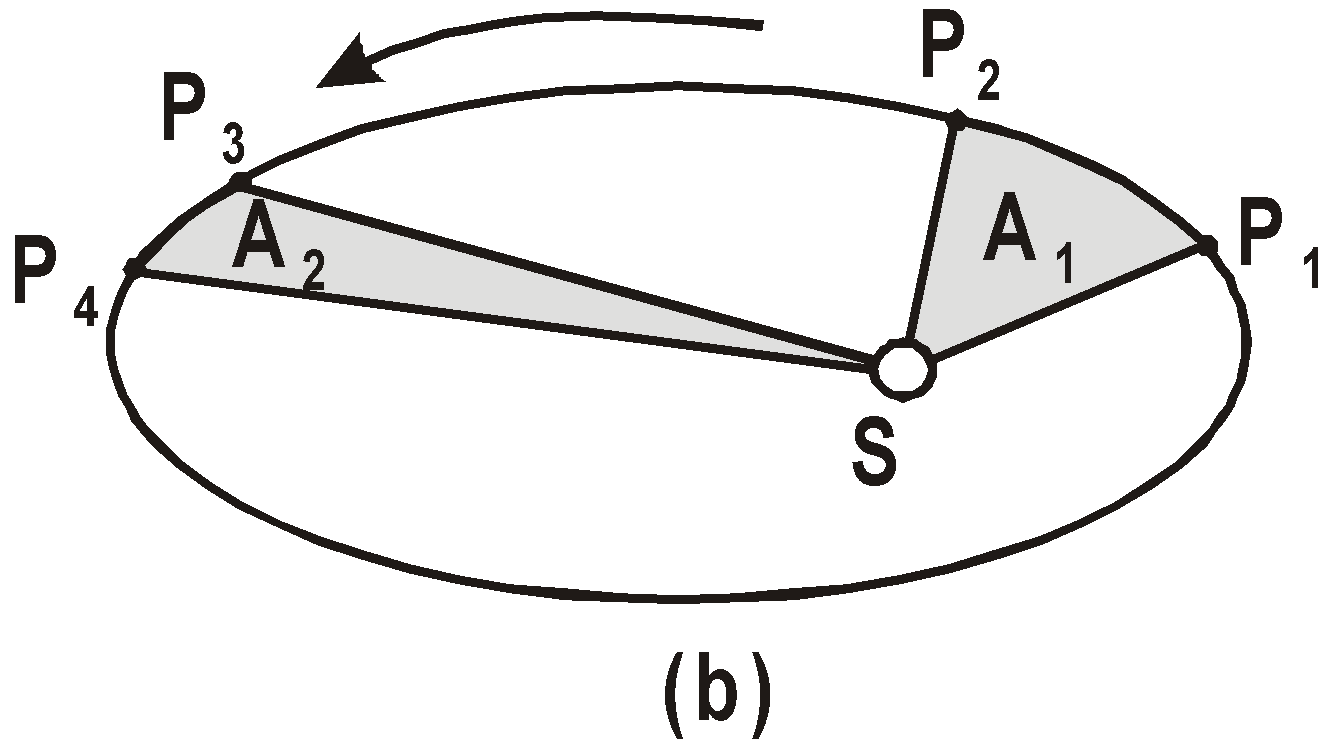
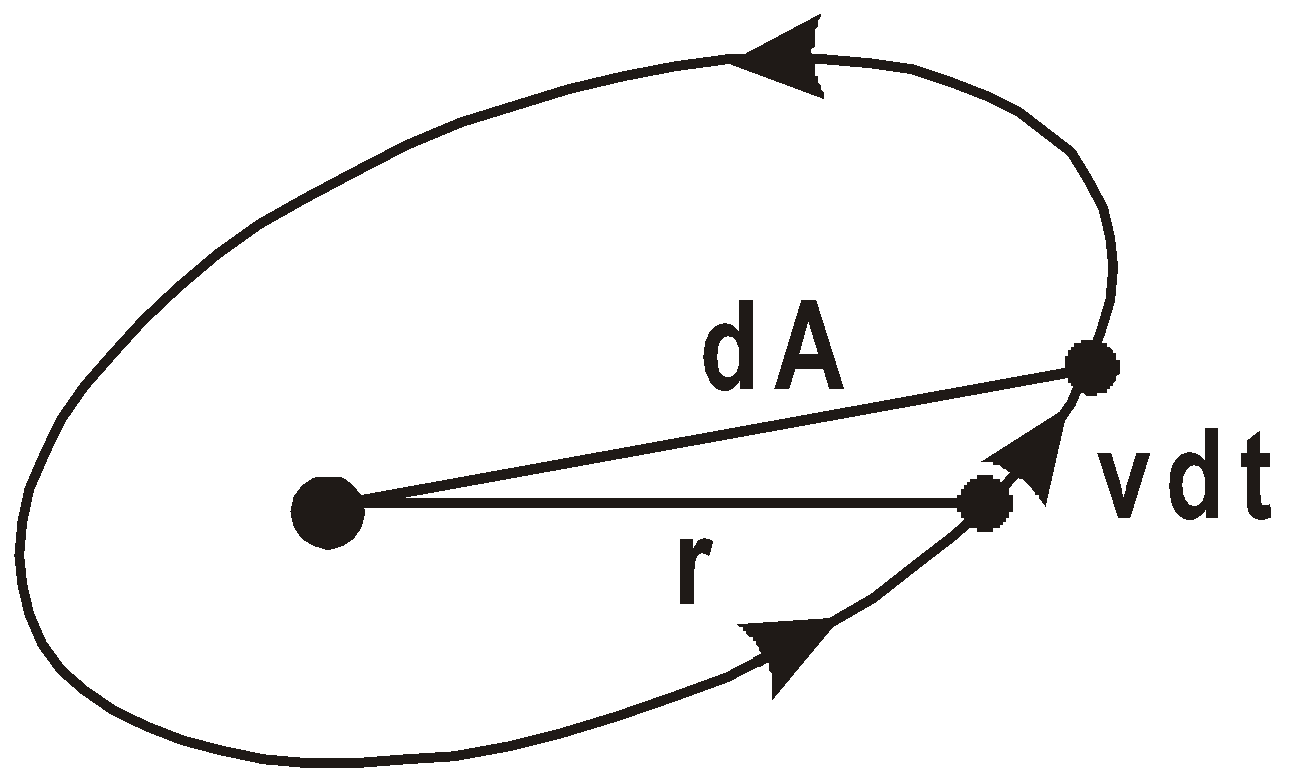
LAW OF AREAS
LAW OF PERIODS
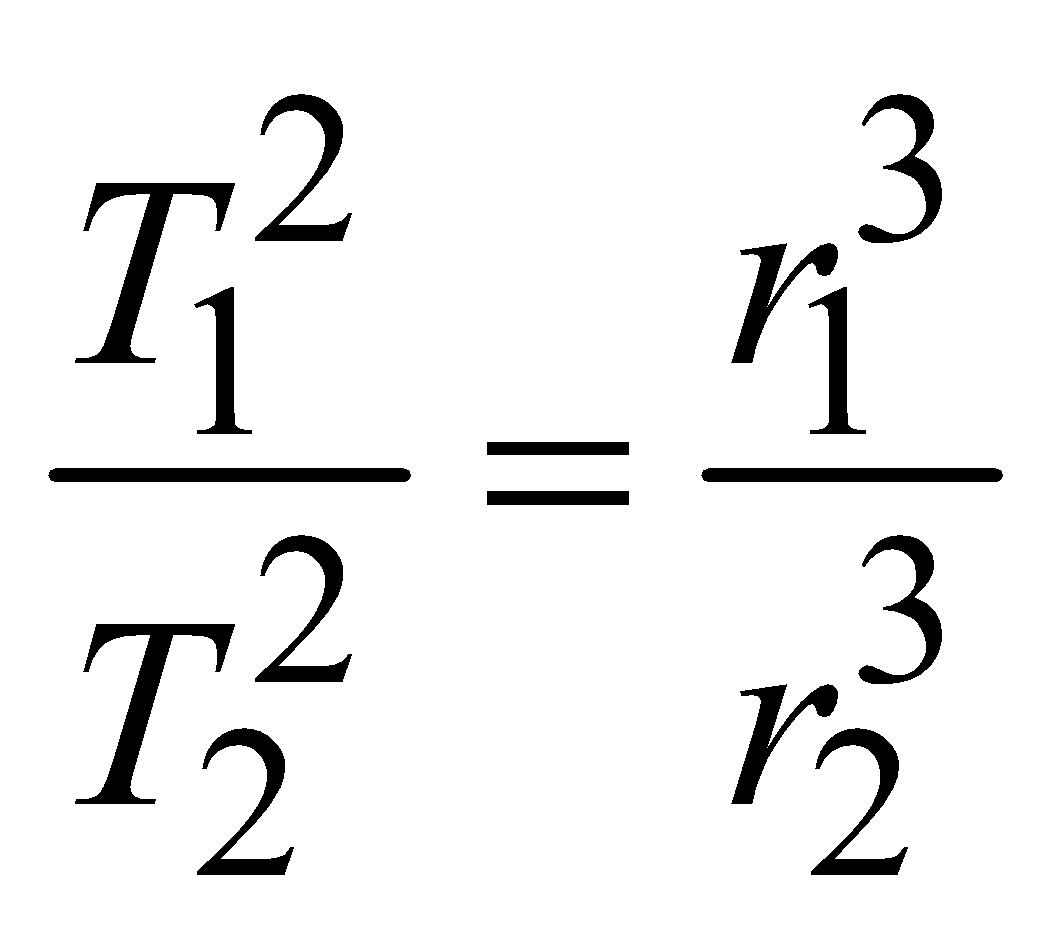
WEIGHTLESSNESS

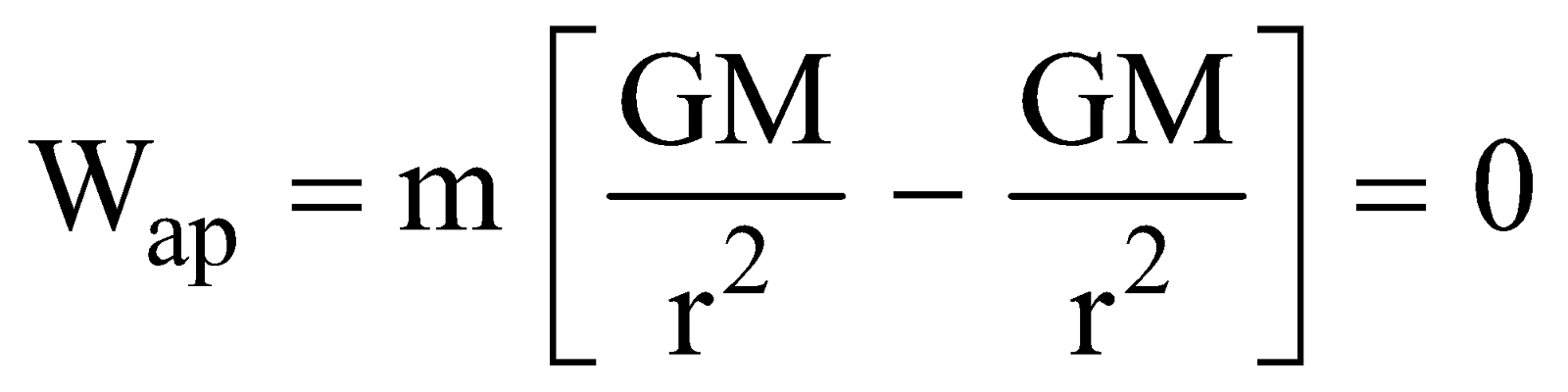
- The moon takes 27.3 days to revolve around the earth.
The radius of its orbit is 3.85 × 105 km. - Kepler’s second law is based on conservation of angular momentum.
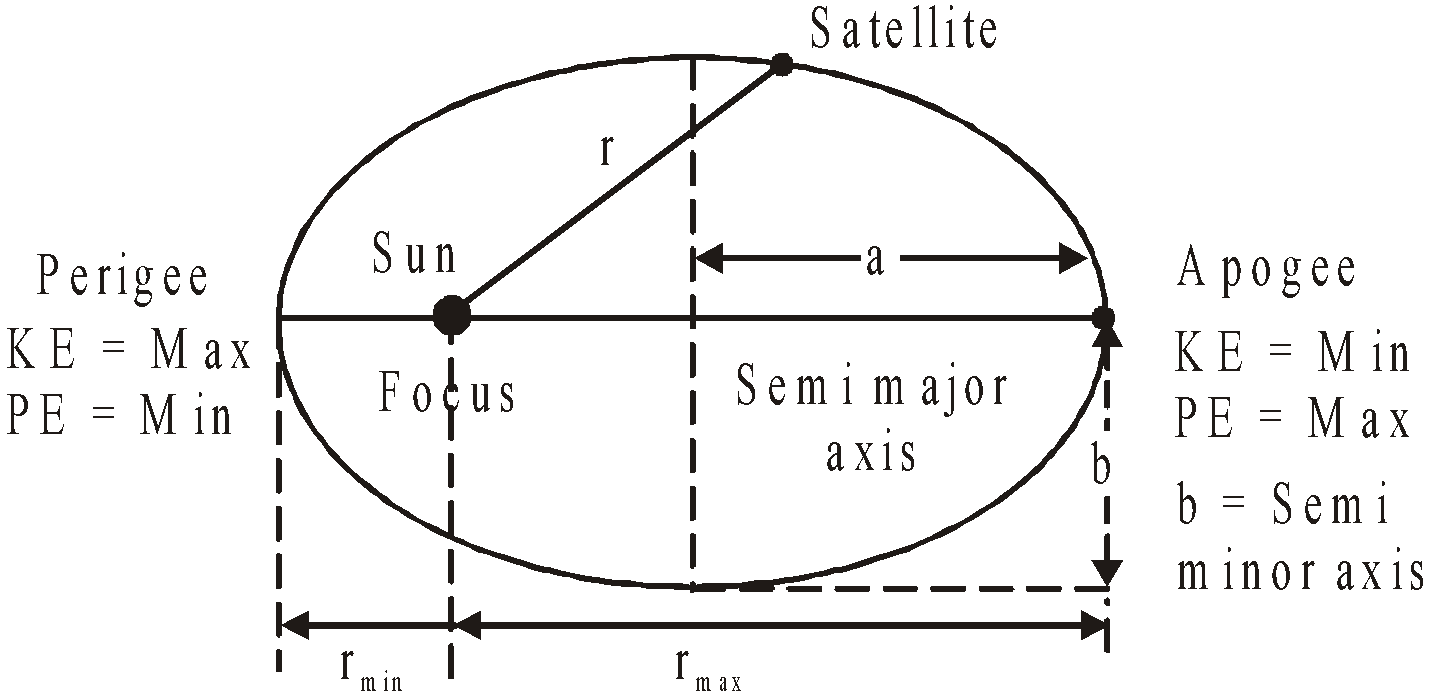
- Perihelion distance is the shortest distance between the sun and the planet.
- Aphelion distance is the largest distance between the Sun and the planet.
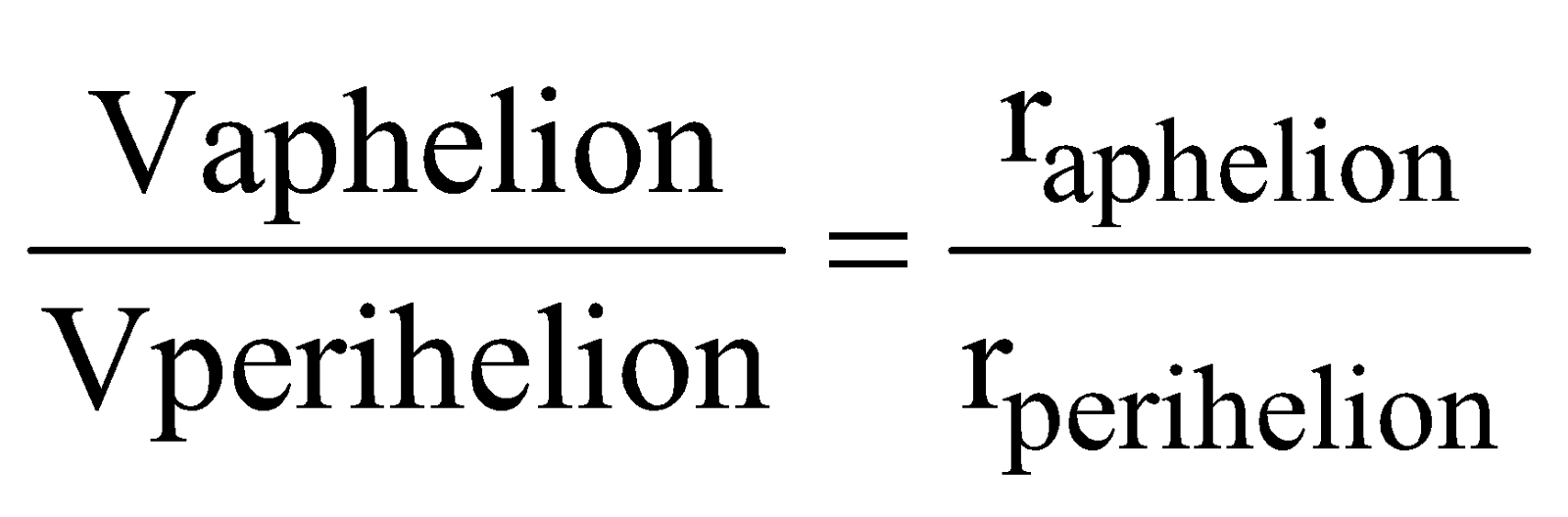
- If e is the eccentricity of the orbit
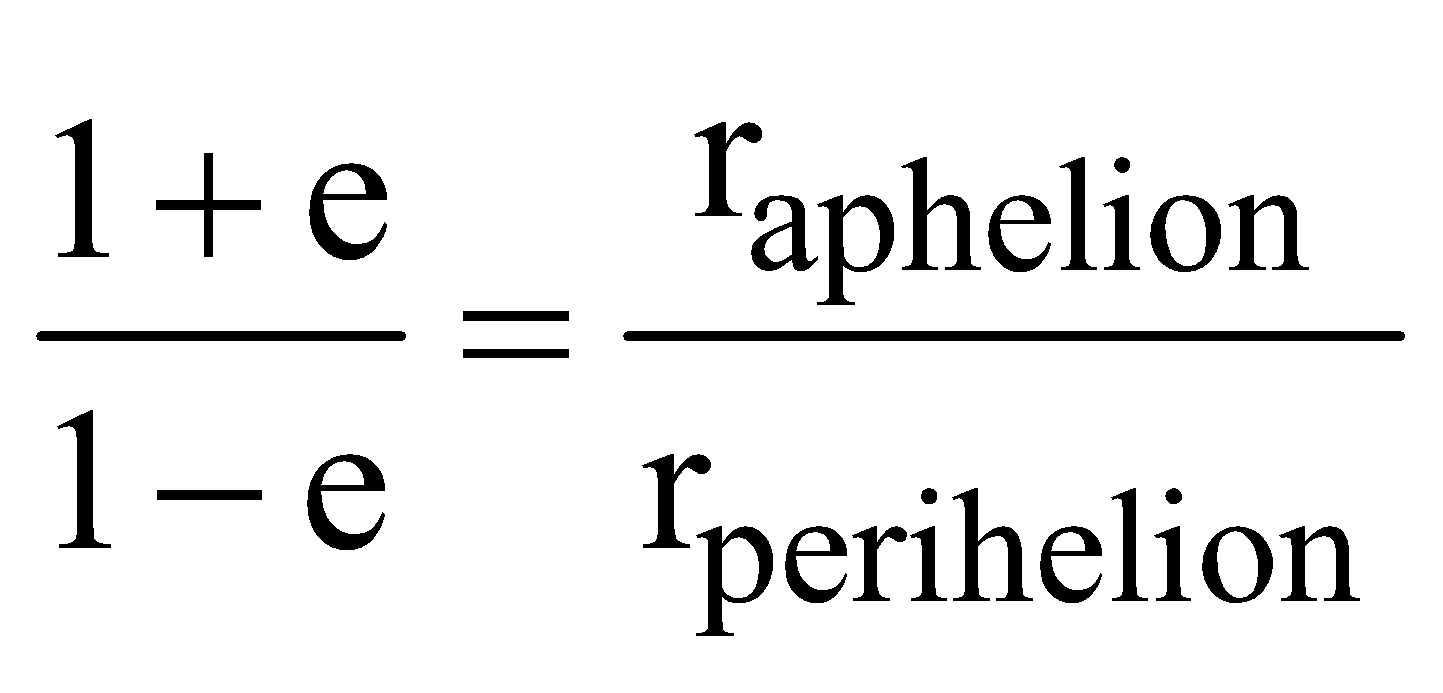
- If e > 1 and total energy (KE + PE) > 0, the path of the satellite is hyperbolic and it escapes from its orbit.
- If e < 1 and total energy is negative it moves in elliptical path.
- If e = 0 and total energy is negative it moves in circular path.
- If e = 0 and total energy is zero it will take parabolic path.
- The path of the projectiles thrown to lower heights is parabolic and thrown to greater heights is elliptical.
- Kepler’s laws may be applied to natural and artificial satellites as well.
- Gravitational force does not depend upon medium so no medium can shield it or block it.
- The escape velocity and the orbital velocity are independent of the mass of the body being escaped or put into the orbit.