IB DP Physics: Topic 9. Wave phenomena: 9.5 Doppler effect: Study Notes

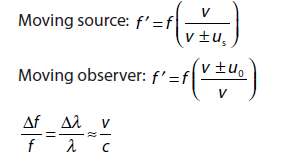
DOPPLER EFFECT

When a source of sound and an observer or both are in motion relative to each other there is an apparent change in frequency of sound as heard by the observer. This phenomenon is called the Doppler’s effect.Apparent change in frequency

1. When source is in motion and observer at rest
   
   1. when source moving towards observer

2. 2. when source moving away from observer

Here V = velocity of sound VS = velocity of sourceν0 = source frequency.

2. When source is at rest and observer in motion
   
   1. when observer moving towards source

2. 2. when observer moving away from source and
      V0 = velocity of observer.

3. When source and observer both are in motion
   
   1. If source and observer both move away from each other.

2. 2. If source and observer both move towards each other.

When the wind blows in the direction of sound, then in all above formulae V is replaced by (V + W) where W is the velocity of wind. If the wind blows in the opposite direction to sound then V is replaced by (V – W).

The equation for doppler effect may be generalised as

\(\nu _o=\nu_s(\frac{v\pm v_o}{v\pm v_s})\)

where, \(v\) = speed of sound in the medium.

\(v_o\) = speed of the observer with respect to the medium, considered positive when it moves towards the source and negative when it moves away from the source and

\(v_o\) = speed of the source with respect to the medium, considered positive when it moves towards the observer and negative when it moves away from the observer.

DOPPLER EFFECT FOR LIGHT

When a light source and a light detector move relative to each other, the wavelength of the light as measured in the rest frame of the source is the proper wavelength \(\lambda_o\). The detected wavelength \(\lambda\) is either longer (a red shift) or shorter (a blue shift) depending on whether the source–detector separation is increasing or decreasing.

When the separation is increasing, the wavelengths are related by

\(\lambda =\lambda_o\sqrt{\frac{1+\beta}{1-\beta}}\) (source and detector separating),
where \(\beta =\frac{v}{c}\) and \( v\) is the relative radial speed (along a line through the source and detector). If the separation is decreasing, the signs in front of the b symbols are reversed.

For speeds much less than c, the magnitude of the Doppler wavelength shift \(\Delta \lambda= \lambda- \lambda_o \) is approximately related to \(v\)  by

\(v=\frac{\left | \Delta \lambda \right |}{\lambda_o}c \;\;\;\;(v< <c)\)

In terms of frequencies

Suppose a star (or any other light source) moves away from us with a radial speed \(v\) that is low enough (\(beta\) is small enough) for us to neglect the \(\beta^2\)

\(f=f_o (1-\beta)\)
or
\(\frac{f}{f_o} =1- \beta\)
or
\(1 -\frac{f}{f_o} =\beta\)
\(\frac{f_o-f}{f_o}=\beta\)
or
\(\frac{\Delta f}{f_o}=\beta=\frac{v}{c}\)

KEEP IN MEMORY

1. The motion of the listener causes change in number of waves received by the listener and this produces an apparent change in frequency.
2. The motion of the source of sound causes change in wavelength of the sound waves, which produces apparent change in frequency.
3. If a star goes away from the earth with velocity v, then the frequency of the light emitted from it changes from ν to ν’.

ν’ = ν (1–v/c), where c is the velocity of light and  where  is called Doppler’s shift.
If wavelength of the observed waves decreases then the object from which the waves are coming is moving towards the listener and vice versa.