IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 9.5
Topic 9 Weightage : 5 %
All Questions for Topic 9.5 – The Doppler effect for sound waves and light waves
Question
On approaching a stationary observer, a train sounds its horn and decelerates at a constant rate. At time t the train passes by the observer and continues to decelerate at the same rate.
Which diagram shows the variation with time of the frequency of the sound measured by the observer?
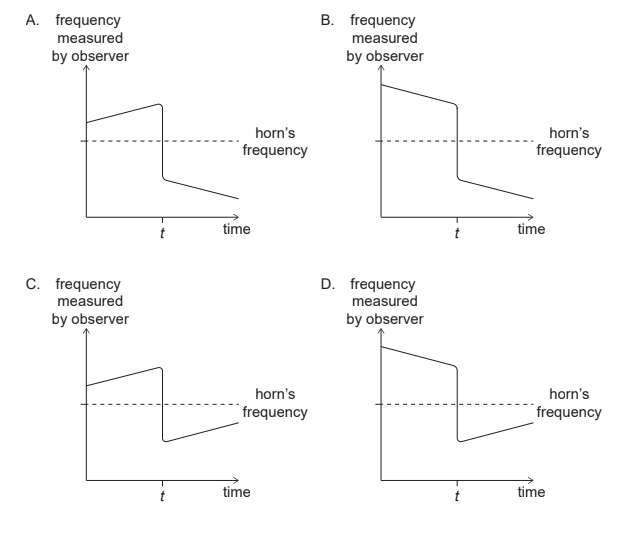
▶️Answer/Explanation
Ans: D
The equation for doppler effect may be generalised as
\(\nu _o=\nu_s(\frac{v\pm v_o}{v\pm v_s})\)
where, \(v\) = speed of sound in the medium.
\(v_o\) = speed of the observer with respect to the medium, considered positive when it moves towards the source and negative when it moves away from the source and
\(v_o\) = speed of the source with respect to the medium, considered positive when it moves towards the observer and negative when it moves away from the observer.
Here in the problem , when Train approached stationary observer , frequency of the sound measured by the observer is given by
\(\nu _o=\nu_s(\frac{v+ 0}{v- v_s})=\nu_s(\frac{v}{v- v_s})\)
Gien train is de-accelerating mean
\(v_s=v_{s0}-at\) or \( v- v_s = v-(v_{s0}-at)=v-v_{s0}+at\)
or
\(\nu _o =\nu_s\frac{v}{k+at}\) where k is \(v-v_{s0}\)
hence as \(t \uparrow \nu_o \downarrow\)
when Train approached leave observer , frequency of the sound measured by the observer is given by
\(\nu _o=\nu_s(\frac{v+ 0}{v+ v_s})=\nu_s(\frac{v}{v+ v_s})\)
Gien train is de-accelerating mean
\(v_s=v_{s0}-at\) or \(v+ v_s = v+(v_{s0}-at)=v+v_{s0}-at\)
or
\(\nu _o =\nu_s\frac{v}{k-at} \;where\; k \;is\; v+v_{s0}\)
hence as \(t \uparrow \nu_o \uparrow\)
This is in answer option D
Question

▶️Answer/Explanation
Markscheme
\(\Delta f’=-\frac{v}{c}{f_o}\)
\(f’-f_o=-\frac{v}{c}{f_o}\)
\(f’=f_o -\frac{v}{c}{f_o}\)
Frequency observed by Gun after reflection from car
\(\frac{\Delta f”}{f’}=-\frac{v}{c}\)
or
\(\Delta f” =-\frac{v}{c}{f’} =-\frac{v}{c} \times (f_o -\frac{v}{c}{f_o})\)
\(f”-f’ =f_o (-\frac{v}{c} + \frac{v^2}{c^2})\)
\(f” =f’+f_o (-\frac{v}{c} + \frac{v^2}{c^2})\)
\(=f_o -\frac{v}{c}{f_o} +f_o (-\frac{v}{c} + \frac{v^2}{c^2})\)
\(=f_o(1-2\frac{v}{c} +\frac{v^2}{c^2})\)
Question
A stationary source of sound emits sound of frequency f. A moving observer measures the sound as having the frequency f ′. The observer is moving directly away from the source at a speed that is 30% of the speed of sound in air.
Which of the following gives the correct value for \(\frac{{f’}}{f}\)?
A. \(\frac{7}{{10}}\)
B. \(\frac{10}{{13}}\)
C. \(\frac{13}{{10}}\)
D. \(\frac{10}{{7}}\)
▶️Answer/Explanation
Markscheme
A
The equation for doppler effect may be generalised as
\(f’=f(\frac{v\pm v_o}{v\mp v_s})\)
In the given case \(v_s=0\) and \(v_o = 0.3v_s\)
Hence
\(\frac{f’}{f}=\frac{v-v_o}{v}=\frac{v-0.3v}{v}=0.7=\frac{7}{10}\)
Question
During a journey an observer travels at constant speed towards, and then goes beyond, a stationary emitter of sound.
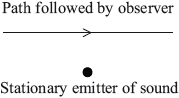
The frequency of the sound as measured at the emitter is \(f\). The frequency according to the observer
A. is always greater than \(f\).
B. is always equal to \(f\).
C. is always less than \(f\).
D. varies during the journey.
▶️Answer/Explanation
Markscheme
D
Doppler shift is given by
\(f’=f(\frac{v\pm v_o}{v\mp v_s})\)
when Observer going towards stationary source \(v_s=0\) and \(v_o\) is positive
\(f’=f(\frac{v+ v_o}{v})\)
when Observer going away from stationary source \(v_s=0\) and \(v_o\) is negative
\(f’=f(\frac{v- v_o}{v})\)
Question
Which of the following wave phenomena is associated with blood flow measurements?
A. Polarization
B. Diffraction
C. Refraction
D. Doppler effect
▶️Answer/Explanation
Markscheme
D
Doppler effect is utilizes to measure movement or flow in the body.
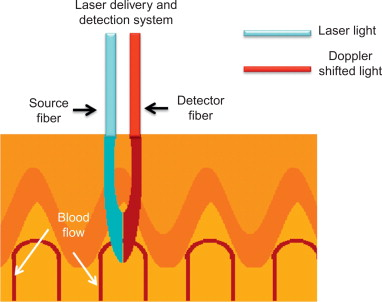
Question
A source of sound approaches a stationary observer. The speed of the emitted sound and its wavelength, measured at the source, are \(\nu \) and \(\lambda \) respectively. Which of the following is the wave speed and the wavelength, as measured by the stationary observer?
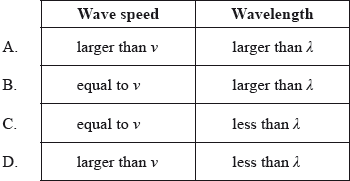
▶️Answer/Explanation
Markscheme
C
\(f’=f(\frac{v\pm v_o}{v\mp v_s})\)
when source of going towards stationary observer \(v_0=0\) and \(v_s\) is negative
Hence
\(f’=f(\frac{v+0}{v-v_s})=f(\frac{v}{v-v_s})\) hence \(f’ >f\)
Now \(v = f\lambda\)
hence \(\lambda'<\lambda\) . Speed of sound = wave speed does not change