Question
A solid piece of chocolate of mass \(82 \mathrm{~g}\) is placed in a pan over fire. Thermal energy is transferred to the chocolate at a constant rate. The graph shows the variation with time \(t\), of the temperature \(T\) of the chocolate. At 6.0 minutes all the chocolate has melted.
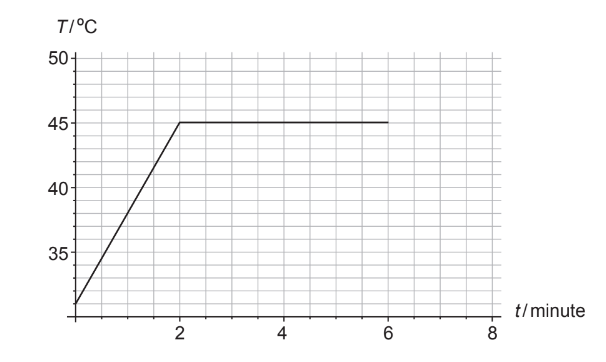
The specific heat capacity of solid chocolate is \(1.6 \times 10^3 \mathrm{~J} \mathrm{~kg}^{-1} \mathrm{~K}^{-1}\).
(a) Show that the average rate at which thermal energy is transferred into the chocolate is about \(15 \mathrm{~W}\).[3]
(b) Estimate the specific latent heat of fusion of chocolate.[2]
(c) Compare the internal energy of the chocolate at t = 2 minutes with that at t = 6 minutes. [2]
▶️Answer/Explanation
Ans:
Reads change in temperature to be \(45-31\) OR 14 ‘ \(\mathrm{C} V\)
$
Q=0.082 \times 1.6 \times 10^3 \times 14=1.84 \times 10^3 \alpha \mathrm{J} n
$
$
P=\frac{1.84 \times 10^3}{2.0 \times 60}=15.3 \approx 15 \ll W_n
$
b.\(\begin{aligned} & Q=15.3 \times 4.0 \times 60=3.67 \times 10^3 \ll \mathrm{J} » \\ & L=\frac{3.67 \times 10^3}{0.082}=4.5 \times 10^4 \alpha \mathrm{J} \mathrm{kg}^{-1} »\end{aligned}\)
c.Internal energy is greater at \(t=6 \mathrm{~min} O R\) internal energy is lower at \(t=2 \mathrm{~min} O R\) internal energy increases «as energy is added to the system»
Because kinetic energy «of the molecules» is the same AND potential energy w of the molecules was increased / OWTTE
Question
A sample of vegetable oil, initially in the liquid state, is placed in a freezer that transfers thermal energy from the sample at a constant rate. The graph shows how temperature T of the sample varies with time t.
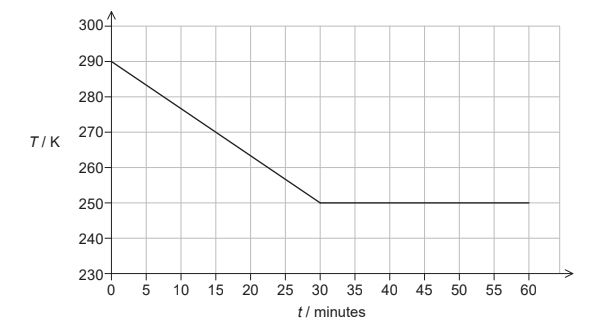
The following data are available.
Mass of the sample = 0.32 kg
Specific latent heat of fusion of the oil = 130 kJ kg–1
Rate of thermal energy transfer = 15 W
(a ) (i) Calculate the thermal energy transferred from the sample during the first 30 minutes. [1]
(ii) Estimate the specific heat capacity of the oil in its liquid phase. State an appropriate unit for your answer. [2]
(b) The sample begins to freeze during the thermal energy transfer. Explain, in terms of the molecular model of matter, why the temperature of the sample remains constant during freezing. [3]
(c) Calculate the mass of the oil that remains unfrozen after 60 minutes. [2]
Answer/Explanation
Ans:
a i « » 15 × 30 × 60 » = 27000 «J»
a ii 27 × 10 3 = 0.32 × c × (290 250) OR 2100 J kg-1 K-1 OR J kg-1 0C-1
b
«intermolecular» bonds are formed during freezing
bond-forming process releases energy
OR
«intermolecular» PE decreases «and the difference is transferred as heat»
«average random» KE of the molecules does not decrease/change
temperature is related to «average» KE of the molecules «hence unchanged»
c
mass of frozen oil « = \(\frac{27\times 10^3}{130\times 10^3}\) » 0.21 «kg»
unfrozen mass «= 0.32 – 0.21»= 0.11 «kg »