10.1 The Ideal Spring and Simple Harmonic Motion
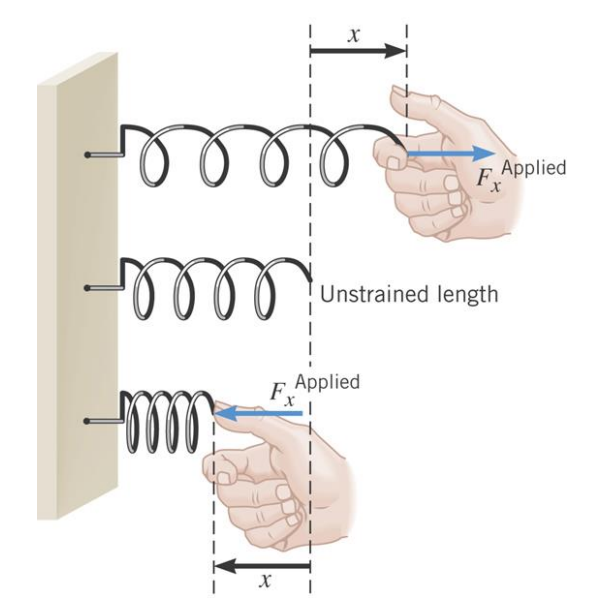
$
F_x^{\text {Applied }}=\underset{\imath}{k x}
$
spring constant
Units: \(\mathrm{N} / \mathrm{m}\)
Example 1 A Tire Pressure Gauge

The spring constant of the spring is \(320 \mathrm{~N} / \mathrm{m}\) and the bar indicator extends \(2.0 \mathrm{~cm}\). What force does the air in the tire apply to the spring?
▶️Answer/Explanation
Ans:

\(\begin{aligned} & F_x^{\text {Applied }}=k x \\ & =(320 \mathrm{~N} / \mathrm{m})(0.020 \mathrm{~m})=6.4 \mathrm{~N}\end{aligned}\)
Conceptual Example 2 Are Shorter Springs Stiffer?

A 10-coil spring has a spring constant \(k\). If the spring is cut in half, so there are two 5-coil springs, what is the spring constant of each of the smaller springs?
HOOKE’S LAW: RESTORING FORCE OF AN IDEAL SPRING
The restoring force on an ideal spring is \(\quad F_x=-k x\)

10.2 Simple Harmonic Motion and the Reference Circle
DISPLACEMENT


\(x=A \cos \theta=A \cos \omega t\)
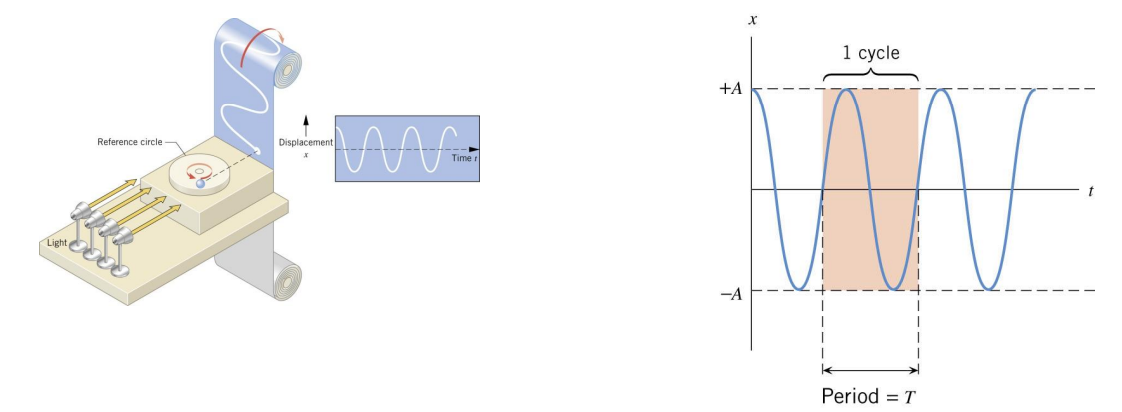
amplitude \(A\) : the maximum displacement
period \(T\) : the time required to complete one cycle
frequency \(f\) : the number of cycles per second (measured in \(\mathrm{Hz}\) )
$
f=\frac{1}{T} \quad \omega=2 \pi f=\frac{2 \pi}{T}
$
VELOCITY

\(v_x=-v_T \sin \theta=-\underbrace{A \omega}_{v_{\max }} \sin \omega t\)
Example 3 The Maximum Speed of a Loudspeaker Diaphragm
The frequency of motion is \(1.0 \mathrm{KHz}\) and the amplitude is \(0.20 \mathrm{~mm}\).
(a) What is the maximum speed of the diaphragm?
(b) Where in the motion does this maximum speed occur?

$
\begin{aligned}
& v_x=-v_T \sin \theta=-\underbrace{A \omega}_{v_{\max }} \sin \omega t \\
& \text { (a) } v_{\max }=A \omega=A(2 \pi f)=\left(0.20 \times 10^{-3} \mathrm{~m}\right)(2 \pi)\left(1.0 \times 10^3 \mathrm{~Hz}\right) \\
& =1.3 \mathrm{~m} / \mathrm{s}
\end{aligned}
$
▶️Answer/Explanation
Ans:
(a)
$
\begin{aligned}
& v_{\max }=A \omega=A(2 \pi f)=\left(0.20 \times 10^{-3} \mathrm{~m}\right)(2 \pi)\left(1.0 \times 10^3 \mathrm{~Hz}\right) \\
& =1.3 \mathrm{~m} / \mathrm{s}
\end{aligned}
$

(b)The maximum speed occurs midway between the ends of its motion.
ACCELERATION

\(a_x=-a_c \cos \theta=-\underbrace{A \omega^2}_{a_{\max }} \cos \omega t\)
FREQUENCY OF VIBRATION
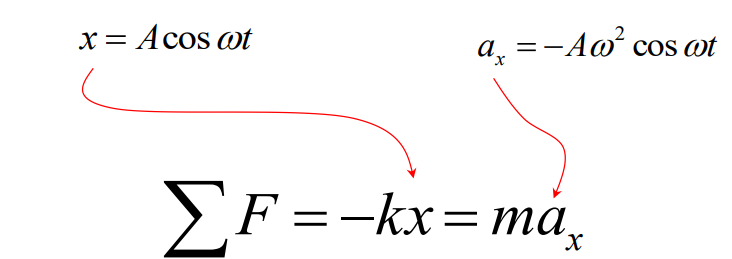
\(-k A=-m A \omega^2\)
\(\omega=\sqrt{\frac{k}{m}}\)
Example 6 A Body Mass Measurement Device
The device consists of a spring-mounted chair in which the astronaut sits. The spring has a spring constant of \(606 \mathrm{~N} / \mathrm{m}\) and the mass of the chair is \(12.0 \mathrm{~kg}\). The measured period is \(2.41 \mathrm{~s}\). Find the mass of the astronaut.

\(\omega=\sqrt{\frac{k}{m_{\text {total }}}}\)
\(m_{\text {total }}=k / \omega^2\)
\(\omega=2 \pi f=\frac{2 \pi}{T}\)
\(m_{\text {total }}=\frac{k}{(2 \pi / T)^2}=m_{\text {chair }}+m_{\text {astro }}\)
\(\begin{aligned} & m_{\text {astro }}=\frac{k}{(2 \pi / T)^2}-m_{\text {chair }} \\ & =\frac{(606 \mathrm{~N} / \mathrm{m})(2.41 \mathrm{~s})^2}{4 \pi^2}-12.0 \mathrm{~kg}=77.2 \mathrm{~kg}\end{aligned}\)
10.3 Energy and Simple Harmonic Motion
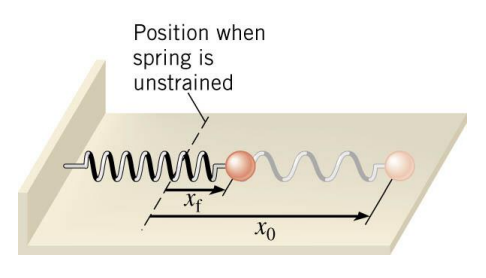
A compressed spring can do work.

\(\begin{gathered}W_{\text {elastic }}=(\bar{F} \cos \theta) s=\frac{1}{2}\left(k x_o+k x_f\right) \cos 0^{\circ}\left(x_o-x_f\right) \\ W_{\text {elastic }}=\frac{1}{2} k x_o^2-\frac{1}{2} k x_f^2\end{gathered}\)

DEFINITION OF ELASTIC POTENTIAL ENERGY
The elastic potential energy is the energy that a spring has by virtue of being stretched or compressed. For an ideal spring, the elastic potential energy is
$
\mathrm{PE}_{\text {elastic }}=\frac{1}{2} k x^2
$
SI Unit of Elastic Potential Energy: joule (J)
Conceptual Example 8 Changing the Mass of a Simple Harmonic Oscilator
The box rests on a horizontal, frictionless surface. The spring is stretched to \(x=A\) and released. When the box is passing through \(x=0\), a second box of the same mass is attached to it. Discuss what happens to the (a) maximum speed (b) amplitude (c) angular frequency.

Example 8 Adding a Mass to a Simple Harmonic Oscillator
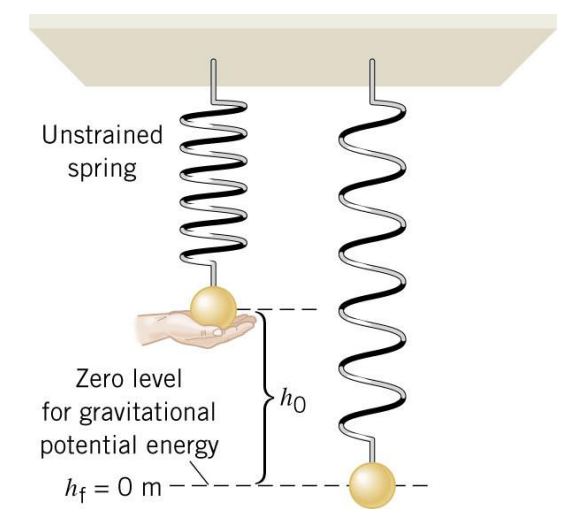
A \(0.20-\mathrm{kg}\) ball is attached to a vertical spring. The spring constant is \(28 \mathrm{~N} / \mathrm{m}\). When released from rest, how far does the ball fall before being brought to a momentary stop by the spring?
\(\begin{gathered}E_f=E_o \\ \frac{1}{2} m v_f^2+\frac{1}{2} I \omega_f^2+m g h_f+\frac{1}{2} k y_f^2=\frac{1}{2} m v_o^2+\frac{1}{2} I \omega_o^2+m g h_o+\frac{1}{2} k y_o^2\end{gathered}\)
\(\frac{1}{2} k h_o^2=m g h_o\)
\(\begin{aligned} & h_o=\frac{2 m g}{k} \\ & =\frac{2(0.20 \mathrm{~kg})\left(9.8 \mathrm{~m} / \mathrm{s}^2\right)}{28 \mathrm{~N} / \mathrm{m}}=0.14 \mathrm{~m}\end{aligned}\)
10.4 The Pendulum
A simple pendulum consists of a particle attached to a frictionless pivot by a cable of negligible mass.
$
\omega=\sqrt{\frac{g}{L}} \quad \text { (small angles only) }
$
Physicalpendulum
$
\omega=\sqrt{\frac{m g L}{I}} \quad \text { (small angles only) }
$
Example 10 Keeping Time
Determine the length of a simple pendulum that will swing back and forth in simple harmonic motion with a period of \(1.00 \mathrm{~s}\).
\(\omega=2 \pi f=\frac{2 \pi}{T}=\sqrt{\frac{g}{L}}\)
\(L=\frac{T^2 g}{4 \pi^2}\)
\(L=\frac{T^2 g}{4 \pi^2}=\frac{(1.00 \mathrm{~s})^2\left(9.80 \mathrm{~m} / \mathrm{s}^2\right)}{4 \pi^2}=0.248 \mathrm{~m}\)
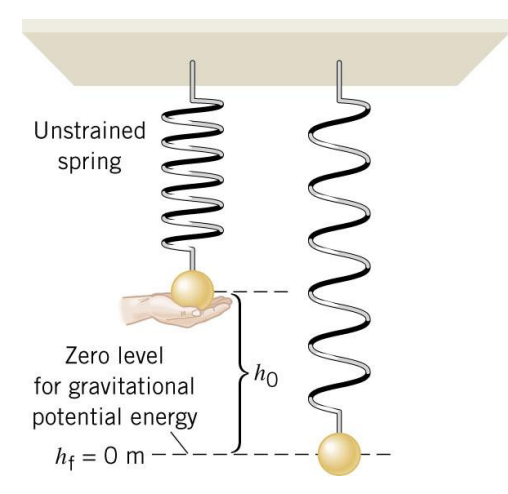
10.5 Damped Harmonic Motion

In simple harmonic motion, an object oscillates with a constant amplitude.
In reality, friction or some other energy dissipating mechanism is always present and the amplitude decreases as time passes.
This is referred to as damped harmonic motion.

1) simple harmonic motion
2\&3) underdamped
4) critically damped
5) overdamped
10.6 Driven Harmonic Motion and Resonance
When a force is applied to an oscillating system at all times, the result is driven harmonic motion.
Here, the driving force has the same frequency as the spring system and always points in the direction of the object’s velocity.
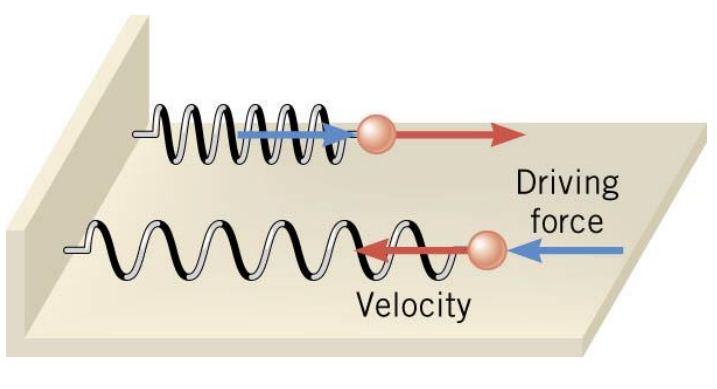
RESONANCE
Resonance is the condition in which a time-dependent applied force can transmit large amounts of energy to an oscillating object, leading to a large amplitude motion.
Resonance occurs when the frequency of the applied force matches a natural frequency at which the object will oscillate.
