Question
(a) 8 15 18 33 39 41 51 57 60 81
From this list, write down
(i) a factor of 54,
………………………………………….
(ii) a multiple of 19,
………………………………………….
(iii) a prime number.
………………………………………….
(b) Write down the reciprocal of 64.
………………………………………….
(c) (i) Write 4.81\times \(10^{-3}\) as an ordinary number.
………………………………………….
(ii) Write 75000 in standard form.
………………………………………….
(iii) Calculate \(\frac{6.3\times 10^{2}}{7\times 10^{-3}}.\)
Write your answer in standard form.
………………………………………….
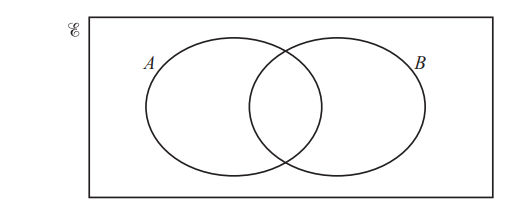
(d) (i)
E = {2, 4, 8, 16, 32, 64}
A = {square numbers}
B = {cube numbers}
Use this information to complete the Venn diagram.
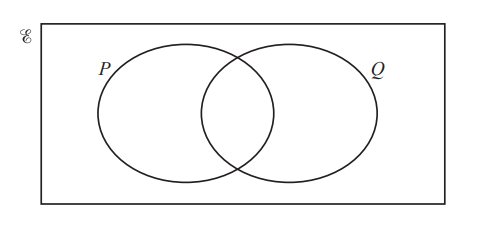
(ii) On this Venn diagram, shade the region \(P\cup Q\).
Answer/Explanation
(a)(i) 18
(ii) 57
(iii) 41
(b)\frac{1}{64}
(c)(i) [0].00481
(ii) \(7.5 ×10^{4}\)
(iii)\(9\times 10^{4}\)
(d)(i)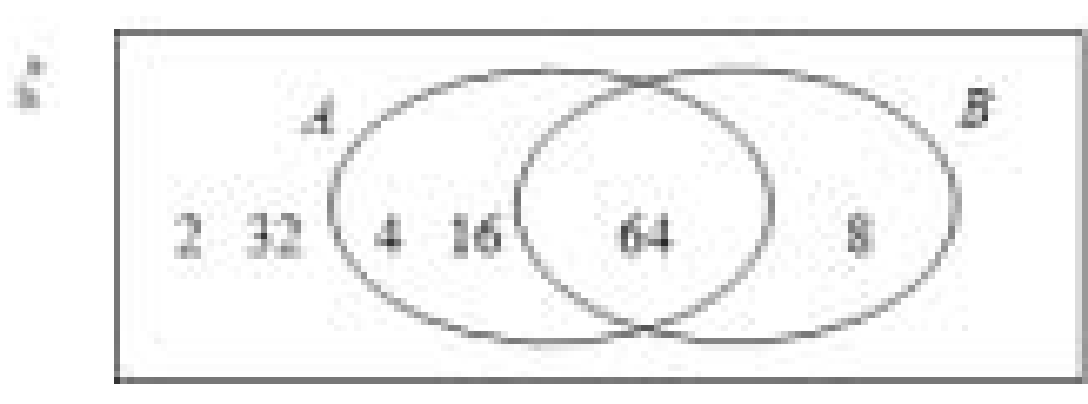
(ii)
Question
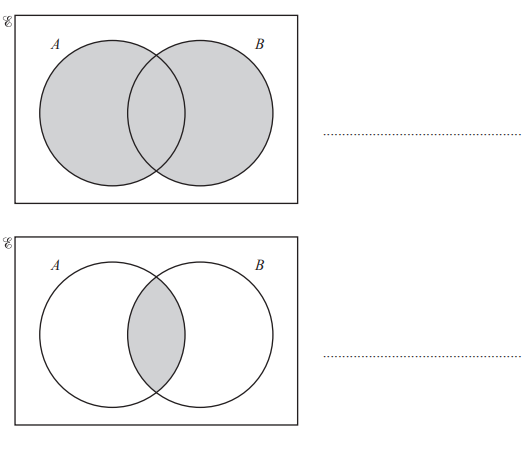
(a) Use set notation to describe the shaded region in each Venn diagram.
(b) E= {x : x is a natural number G15}
F = {x : x is a factor of 12}
O = {x : x is an odd number}
(i) Complete the Venn diagram to show the elements of these sets.
(ii) Write down one number that is in set O, but not in set F.
…………………………………………. [1]
(iii) Find \(n(F\cup O) .\)
…………………………………………. [1]
(iv) A number is chosen at random from E.
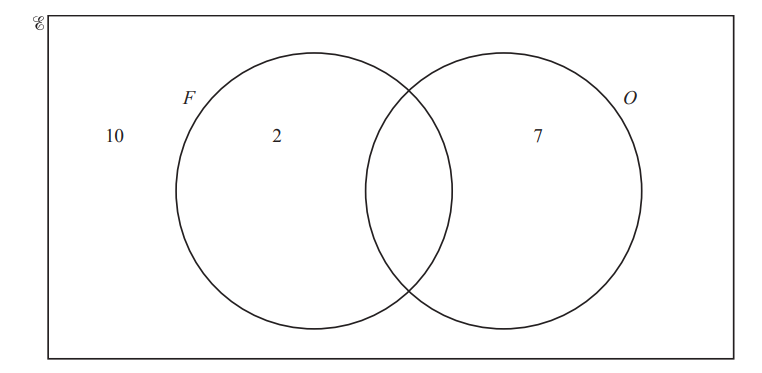
Work out the probability that this number is in set O.
………………………………………….
Answer/Explanation
(a)\(A\cup B A\cap B\)
(b)(i)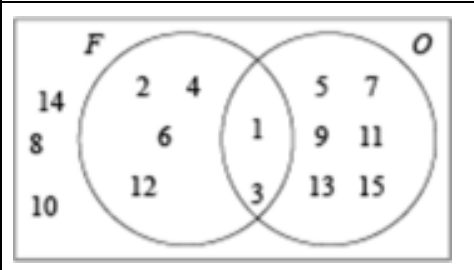
(ii)One of 5, 7, 9, 11, 13, 15
(iii) 12
(iv)\(\frac{8}{15}\)
Question
(a) E = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}
F = {x: x is a factor of 14}
P = {x: x is a prime number less than 14}
(i) Write down the elements in set F.
F = { ………………………………………… }
(ii) Write down the elements in set P.
P = { ………………………………………… }
(iii)
(a) Complete the Venn diagram.
(b) Write down \(n(F\cap P ) .\)
………………………………………….
(c) A number is chosen at random from the universal set E.
Write down the probability that the number is in the set \(F\cup P, \)
………………………………………….
(b) Write 195 as a product of its prime factors.
………………………………………….
Answer/Explanation
(a)(i) 1, 2, 7, 14
(ii) 2, 3, 5, 7, 11, 13
(iii)(a) 1, 14 2, 7 3, 5, 11, 13
4, 6, 8, 9, 10, 12
(b) 2
(c) \(\frac{4}{7}\)
(b) 3 × 5 × 13