12.1 The interaction of matter with radiation
Essential Idea:
The microscopic quantum world offers a range of phenomena, the interpretation and explanation of which require new ideas and concepts not found in the
classical world.
Understandings:
- Photons
- The photoelectric effect
- Matter waves
- Pair production and pair annihilation
- Quantization of angular momentum in the Bohr model for hydrogen
- The wave function
- The uncertainty principle for energy and time and position and momentum
- Tunnelling, potential barrier and factors affecting tunnelling probability
Applications and Skills:
- Discussing the photoelectric effect experiment and explaining which features of the experiment cannot be explained by the classical wave theory of light
- Solving photoelectric problems both graphically and algebraically
- Discussing experimental evidence for matter waves, including an experiment in which the wave nature of electrons is evident
- Stating order of magnitude estimates from the uncertainty principle
Data booklet reference:
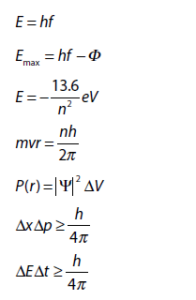
The Interaction of Matter with Radiation
The photoelectric effect
- Definition: Phenomenon in which light (or other forms of electromagnetic radiation) incident on a metallic surface causes electron to be emitted from the surface.
- Experiment: Evacuated tube, with a metallic photo-surface (P), in which light passes through a small opening and causes electrons to be ejected. These electrons are collected by a collecting surface C
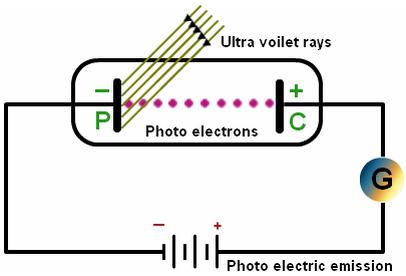
- Since the collecting plate is connected to the negative terminal of the power supply, it will repel normally repel electrons and only absorb the energetic ones.
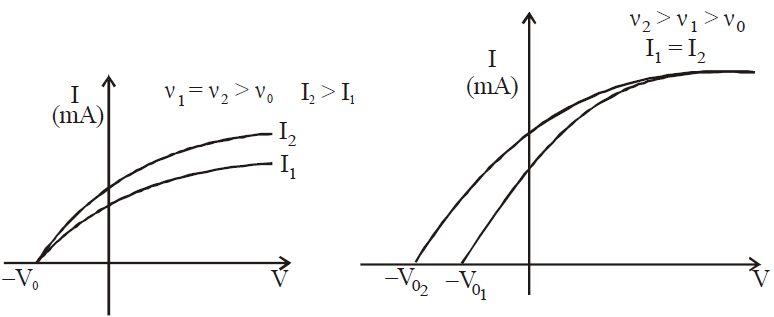
- As the voltage is made more negative, there is a point at which the current ceases, called stopping voltage/potential \(\mathbf{V}_{\mathbf{s}}\)
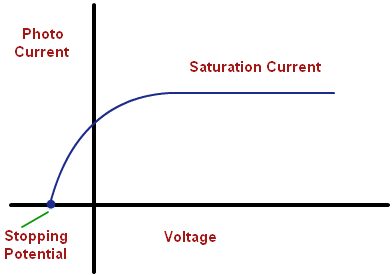
**Tip: **The \(\mathbf{I – V}\) graph will change if the frequency of the light is increased. Each photon will have more energy, and hence, the stopping potential will be greater. The saturation current will depend upon the intensity of the light, but in the case of two lights with the same intensity, the saturation current for the higher frequency will be less. This follows logically from the photon nature of light: Same current means the same amount of electrons (charge-carriers) per second, but higher frequency means that electrons have more energy. Less photons per second means that fewer electrons are emitted, and so, smaller saturation current.
Observations
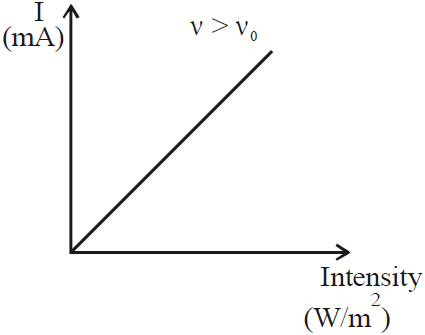
- The intensity of the incident light neither affects the kinetic energy or the stopping voltage, solely the number of electrons emitted.
- The frequency of light influences the emitted electrons’ energy.
- Electrons are emitted without a time delay.
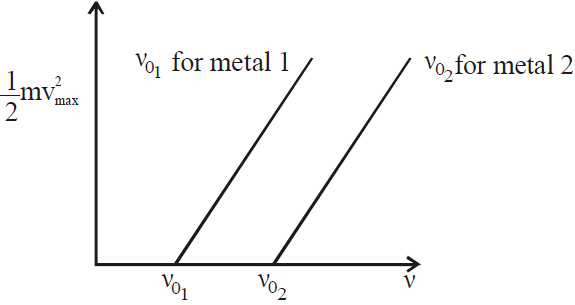
- There is a minimum/threshold frequency,\(\mathbf{\text{fc}}\), below which no electrons are emitted.
If light was only a wave
- Intense beams, which have more energy, should cause the emissions of electrons with higher kinetic energy.
- Frequency should play a role in the energy of electrons
- Low intensity beams should cause a time delay, since energy would need to accumulate before the emission of an electron.
Einstein’s explanation: Light consists of photons, which are quanta or bundles of energy and momentum.
- Photon’s energy:
\(\mathbf{E\ = \ hf\ = \ hc/\lambda}\) - Planck’s constant
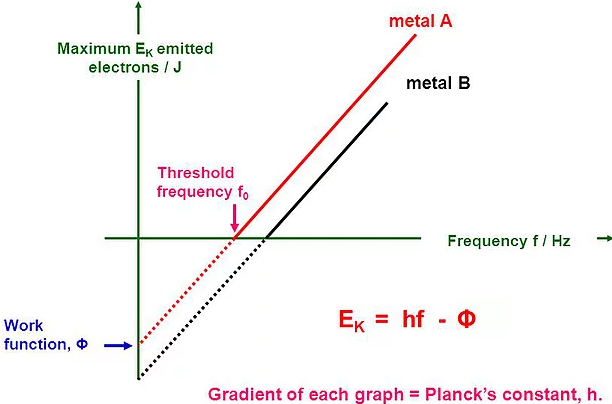
\(\mathbf{= \ h\ = \ 6.63 \times 1}\mathbf{0}^{\mathbf{- 34}}\) - **Photoelectric effect: **Single photon of frequency f is absorbed by a single electron in the photo-surface, so the electron’s energy increases by \(\text{hf}\). The electron will spend
Joules, called the work function, to free itself.
- **Electron’s kinetic energy (after emission): ** E = e Vs = hf – Ф
Matter (or “de Broglie”) Waves
As suggested by de Broglie, to any particle of momentum p, there corresponds a wave of wavelength given by the formula λ = h/p, something known as the duality of matter.
- **Electron diffraction: **Electrons shot through or to a thin slice of crystal have a low probability of reaching a place where the path difference is not an integer number of wavelengths (constructive and destructive interference).
- Electrons accelerated through a pd, they gain kinetic energy. Hence, we have eV = 1/2 mv = p²/2m.
- \(\lambda =hl\sqrt{2meV}\)
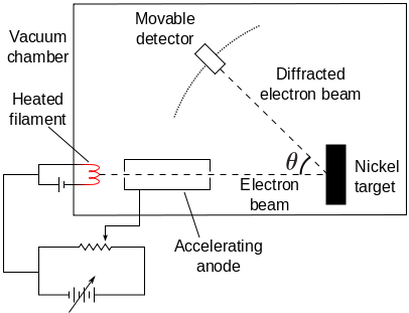
- Davisson-Germer experiment verifies de Broglie hypothesis.
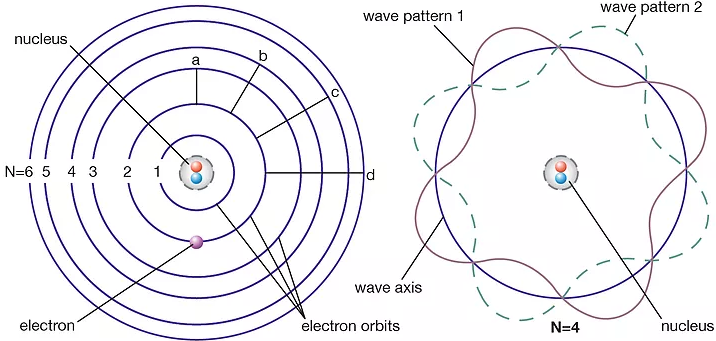
The Bohr Model
Model proposed by Niels Bohr to interpret the scattering of alpha particles, which states that electrons are found at orbitals: fixed multiples of angular momentum that can be represented as a wave function.
- Electrons in any atom have a definite/discrete energy (which explains the emission and absorption spectra).
- Energy levels = electron wave = standing wave, since there is no energy transfer in standing waves
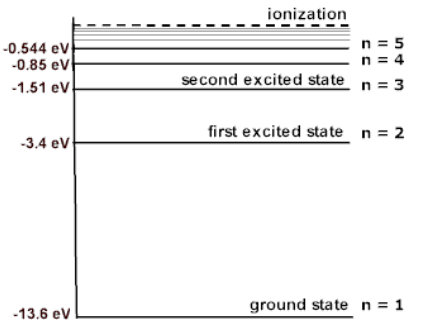
- Hydrogen atom: Energy is given by E = −13.6/n², where n is the principal quantum number and represents the nth energy level.
Hydrogen atom’s electrons
- **Angular momentum (mvr): **A vector product of the momentum of a particle and the radius of its orbit, of an electron in a stationary state is an integral value of h/2π. Hence, we have mvr = nh/2π.
- Assumptions:
- Electrons in an atom exist in stationary states, without emitting any electromagnetic radiation.
- Electrons may move from one stationary state to another by absorbing or emitting a quantum of electromagnetic radiation, with difference in energy between stationary states given by ΔE = hf.
- Limitations Bohr’s Model failed to explain:
- Why some energy transitions are more likely to occur than others
- Predict behavior of other elements
- Explain behaviors theoretically
Schrödinger’s equation (wave function)
Describes the quantum state of the particles, where the square of the amplitude of the wave function │Ψ│²** **is proportional to the probability per unit volume of finding the particle at a distance r from the nucleus
P(r)= │Ψ│2ΔV or at (x,y), i.e. P(x,y) = │Ψ│²ΔV.
- **Copenhagen interpretation: **For double-slit interference, the wave function is considered to be such that a single photon or electron passes through both slits and be everywhere on the screen until it is observed or measured.
- Nothing is real unless it is observed. When observed, the wave function collapses.
Heisenberg’s uncertainty principle
It is impossible to simultaneously measure the position and momentum of a particle with indefinite precision. The same applies to energy and time
- **Uncertainty in position and momentum: ** ΔxΔp ≥ h/4π
- Example: Since we know the wavelength of the electron and momentum and wavelength are related by p = h/λ, Δx is infinite. Single-slit diffraction: The uncertainty in position for beam going through a hole of diameter b is approximately Δx = b/2. When the opening is approximately of the same order as the de Broglie wavelength of the electrons, the wave will diffract.θ
- Uncertainty in energy and time: ∆E∆t ≥ h/4π (where E is half the difference between the excited state and the ground state)
- Useful to estimate the lifetime of an electron in excited state
- **Single-slit diffraction: **The uncertainty in position for beam going through a hole of diameter b is approximately
Δx = b/2. When the opening is approximately of the same order as the de Broglie wavelength of the electrons, the wave will diffract- **Formula: **
ΔxΔp = λp/2 = h/2.
- **Formula: **
- **Electron in a box: **If an electron is confined to a region of length L where it can only move back and forth, the uncertainty in position is
Δx = L/2, and thus, Δp = h/4πΔx = h/2πL.- Kinetic energy = p²/2m = h²/8π²mL²
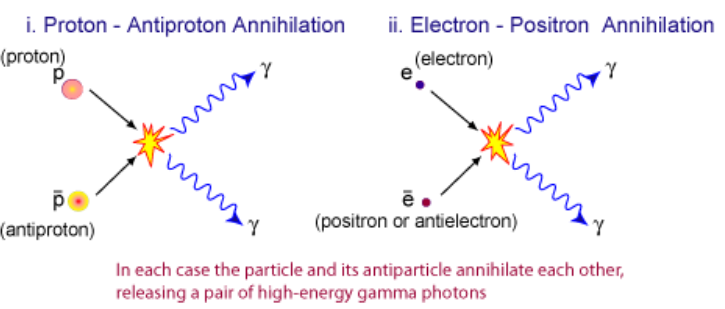
Pair production and annihilation
- Pair production: close to an atomic nucleus, where the electric field is very strong, a photon with minimum energy given by
E = 2mc² can produce a particle and its anti-particle (e.g. e− and e+), where m is the rest mass.- The atomic nucleus helps conserving energy and momentum.
- Any excess energy (above 2mc²) will be converted into kinetic energy of the particles
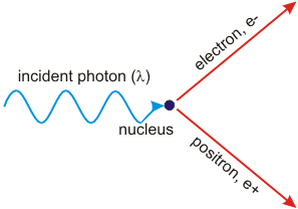
- **Pair annihilation: **when a particle collides with its anti-particle, producing 2 photons
- When they move in the opposite directions, the total energy of the system is
ET = 2(mc² + EK) and the photons will travel in opposite direction.
- When they move in the opposite directions, the total energy of the system is
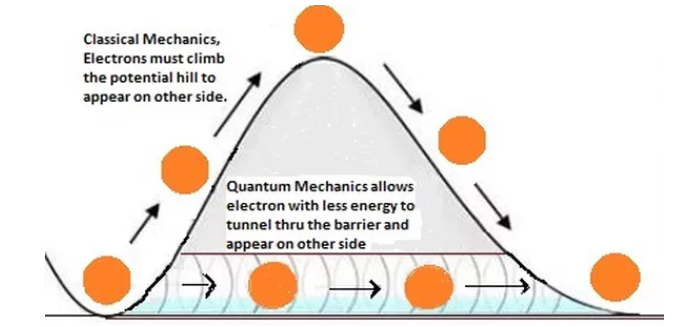
**Quantum Tunneling **
- **Tunneling: **A particle can effectively “borrow” energy from its surroundings, pass through a barrier and pay the energy back
- The energy required to go through a potential barrier is due to the uncertainty principle less than
eV
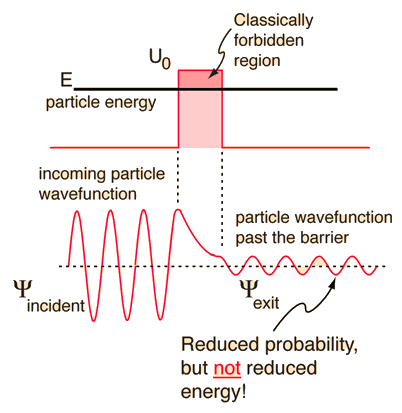
- The wave function is continuous despite the fact that the particle requires more energy to “jump” the barrier, which is borrowed from surroundings
- Energy level remains unchanged after barrier, but the amplitude decreases since it is proportional to P(r)
- In order to increase
P(r), one may reduce:- The mass m of the particles
- The width w of the barrier
- The difference ΔE between the energy barrier and that of the particles
- Responsible for the relatively low temperature fusion that occurs in the Sun and useful in scanning tunneling microscopes (STM).
Nuclear Physics
Rutherford Scattering
Simple energy considerations can be used to calculate the distance of closest approach of an alpha-particle.
- If the alpha-particle initially has kinetic energy upon approaching, when it stops close to the nucleus due to the electrostatic repulsion, the electrical potential energy of the alpha particle will be K(2e)(Ze)/d = 2KZe²/d, where Z is the atom’s proton number.
- An alpha-particle approaching with high kinetic energy will get closer to the nuclear (closest = nuclear radius).
- \(\mathbf{R\ = \ }\mathbf{R}_{\mathbf{0}}\mathbf{A}^{\mathbf{1/3}}\) R is the radius, R0 is the Fermi radius ( \(1.2 \times 10^{- 15}\text{\ m}\)) and A is the mass number.
- All nuclei have the same density, and so their volume is given by
\(\mathbf{V\ = \ 4/3\ \pi}\mathbf{R}^{\mathbf{3}}\mathbf{\ = \ 4/3\ \pi A}{\mathbf{R}_{\mathbf{0}}}^{\mathbf{3}}.\)
- All nuclei have the same density, and so their volume is given by

- Derivations from Rutherford scattering: When the alpha-particles have very high kinetic energy, and thus, the distance of closest approach is equal or less than \(10^{- 15}m\), deviations are observed, which is an evidence of the existence of the strong nuclear force, i.e. they are absorbed.
Electron diffraction
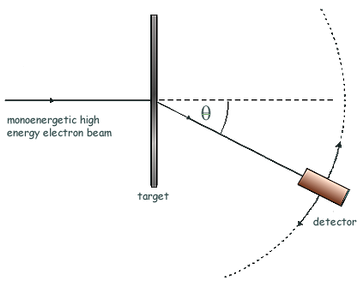
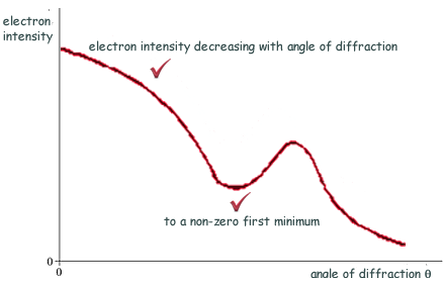
If the de Broglie wavelength λ** **of the electrons is about the same as the nuclear diameter D, then a minimum will be formed at sinθ = λD. **Useful **to measure nuclear radius.
- More accurate than Rutherford scattering, because strong force does not affect electrons.
- When electrons of much higher energy are used, the collisions are no longer elastic and energy is converted into mass, as several mesons are emitted from the nucleus
- At high energies,** **the electrons penetrate into the nucleus and scatter off the quarks within protons and neutrons, something known as deep inelastic scattering, providing evidence for the quark model.
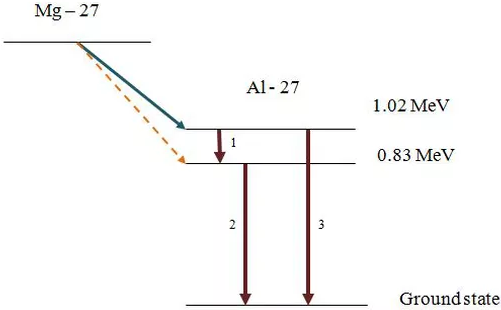
Nuclear energy levels
The emission of alpha and beta particles by radioactive decay often leaves the **daughter nuclei in an excited discrete energy state **(similar to electron energy levels). The state depends on the energy of the alpha or beta particle.
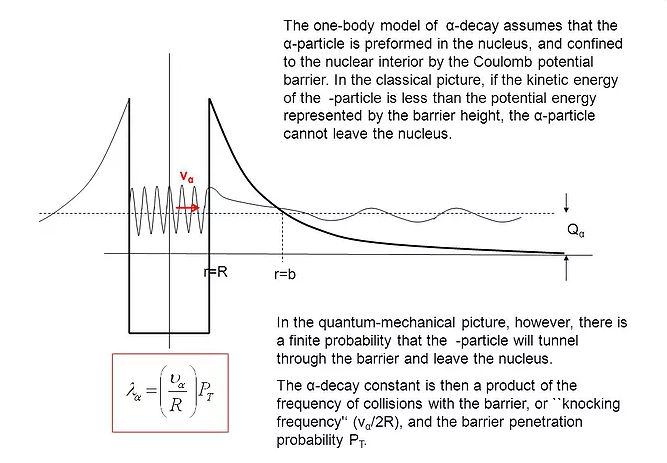
Alpha decay
Alpha-particles form as clusters of two protons and two neutros inside the nucleus well before they are emitted as alpha-particles. This is because the nucleons are in random motion within the nucleus but their kinetic energies are much smaller than those needed to escape.
- The wave function │Ψ│ of the alpha-particles is not localized to the nucleus and allows overlaps with the potential energy barrier provided by the strong nuclear force, which means that there is a finite but very small probability of observing the alpha-particles outside the nucleus (thanks to quantum tunneling).
- Higher potential barriers and greater thickness to cross means a longer lifetime (e.g. polonium).
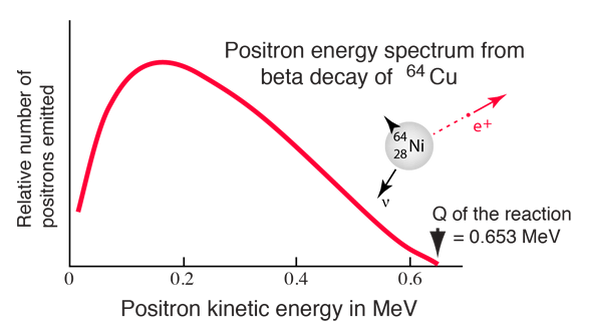
Negative beta decay
Since the beta particles have a continuous energy spectrum, in order to conserve mass, energy, and momentum, the existence of the neutrino was suggested by Pauli (and later anti-neutrino)
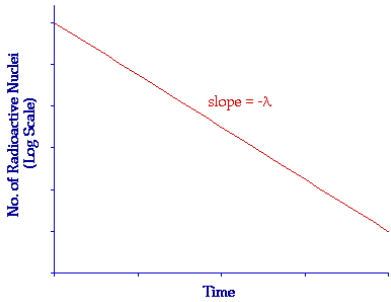
The law of radioactive decay
- Decay constant (λ): The probability that an individual nucleus will decay in a given time interval (e.g.1 s)
- Units:\(s^{- 1},\ min^{- 1},\ hour^{- 1},\ day^{- 1}\text{…\!}\)
- Relationship with half-life:
\(\mathbf{\lambda\ = \ ln(2)/}\mathbf{T}_{\mathbf{half – life}}\) - Activity (A): Number of nuclei decaying in a second in a sample
- Units: becquerel (Bq)
- In a sample of N undecayed nuclei, the activity will be given by n(A) = λN.
- Formulas:
\(\mathbf{N\ = \ }\mathbf{N}_{\mathbf{0}}\mathbf{e}^{\mathbf{- \lambda t}}\mathbf{;\ A\ = \ }\mathbf{A}_{\mathbf{0}}\mathbf{e}^{\mathbf{- \lambda t}}\mathbf{;\ A\ = \ \lambda}\mathbf{N}_{\mathbf{0}}\mathbf{e}^{\mathbf{- \lambda t}}\)where \(\mathbf{A}_{\mathbf{0}}\mathbf{\ = \ \lambda}\mathbf{N}_{\mathbf{0}}\) is the initial activity.
- **Measuring long half-lives: **Not possible to measure using a G-M tube. In these cases, a pure sample of the nuclide in a known chemical form needs to be separated, its mass measured and then a count rate taken. From this reading, the activity can be calculated by multiplying the count rate by the ratio
DUAL NATURE OF RADIATION AND MATTER
CATHODE RAYS
DISCHARGE TUBE EXPERIMENTS
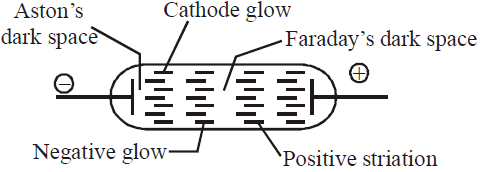
- As pressure is lowered to 0.1 mm. Hg – cathode glow, Crooke’s dark space, negative glow, Faraday’s dark space and striations are observed.
- At a pressure 0.01 mm. Hg entire tube is dark (Crooke’s dark space) except the glass wall behind anode. Colour is yellowish-green for soda glass and greyish-blue for lead glass.
- The luminous streaks travelling from cathode to anode, below the pressure 0.01 mm. Hg, are called cathode rays.
PROPERTIES OF CATHODE RAY
- Emitted perpendicularly to cathode,
- Travel in straight lines
- Carry energy
- Possesses momentum
- Deflected by electric and magnetic fields
- Excite fluorescence
- Ionise gas
- Produce highly penetrating secondary radiation when suddenly stopped
- Effect photographic plate
J.J. THOMSON’S E/M VALUE OF ELECTRON
MILLIKAN’S OIL DROP METHOD FOR E/M
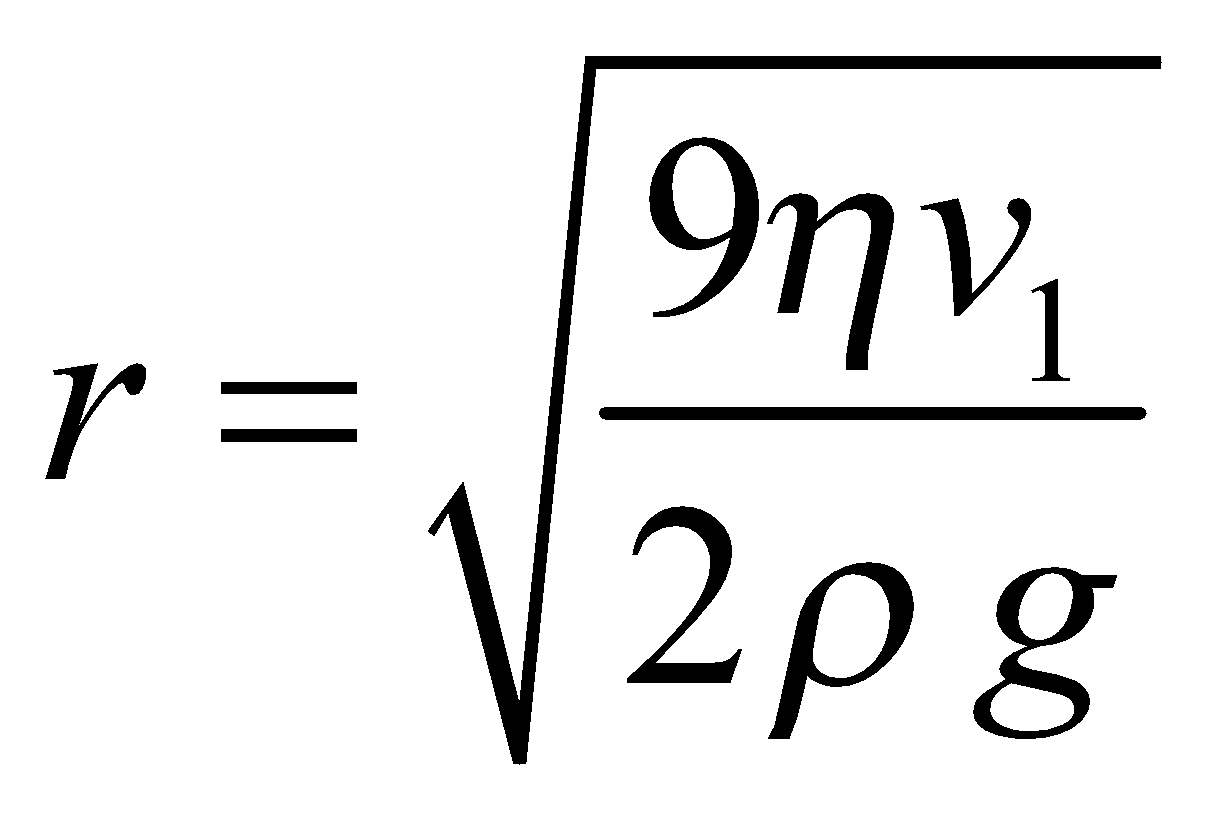 …(4)
…(4)EMISSION OF ELECTRON
- Thermionic emission : The emission of electrons by suitably heating the metal surface.
- Field emission : The emission of electrons by applying very strong field of the order of 108 Vm–1 to a metal.
- Photoelectric emission : The emission of electrons when light of suitable frequency illuminates metal surface.
PHOTOELECTRIC EFFECT (EINSTEIN’S PHOTOELECTRIC EQUATION)
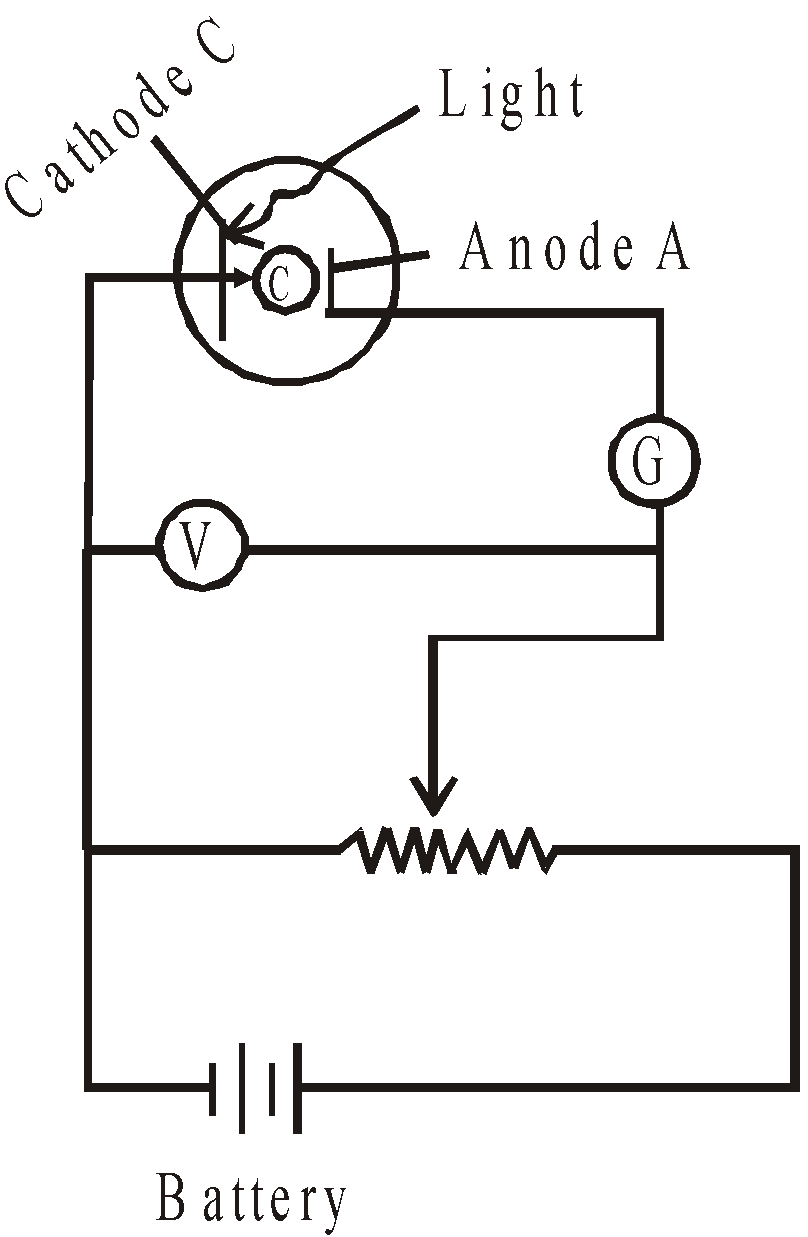
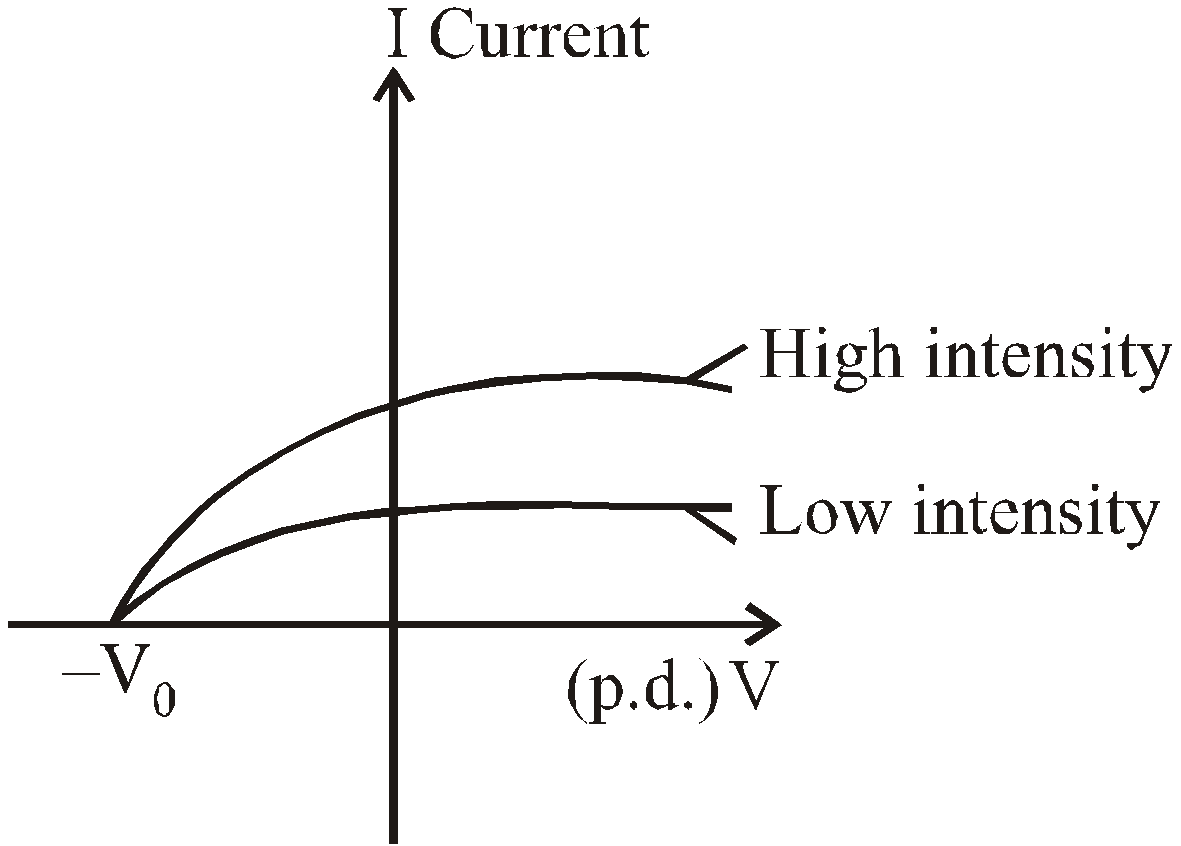
At a voltage less than –V0 the current is zero.
- No photoelectrons are emitted, if the frequency of incident light is less than some cut-off frequency (i.e., threshold frequency) ν0. It is inconsistent with the wave theory of light, which predicts that photoelectric effect occurs at any frequency provided intensity of incident light is sufficiently high.
- The maximum kinetic energy of the photoelectrons is independent of light intensity, but increases with increasing the frequency of incident light.
- Electrons are emitted from surface almost instantaneously (less than 10–9 sec after the surface illumination), even at low intensity of incident light (classically we assume that the electrons would require some time to absorb the incident light before they acquire enough kinetic energy to escape from metal).
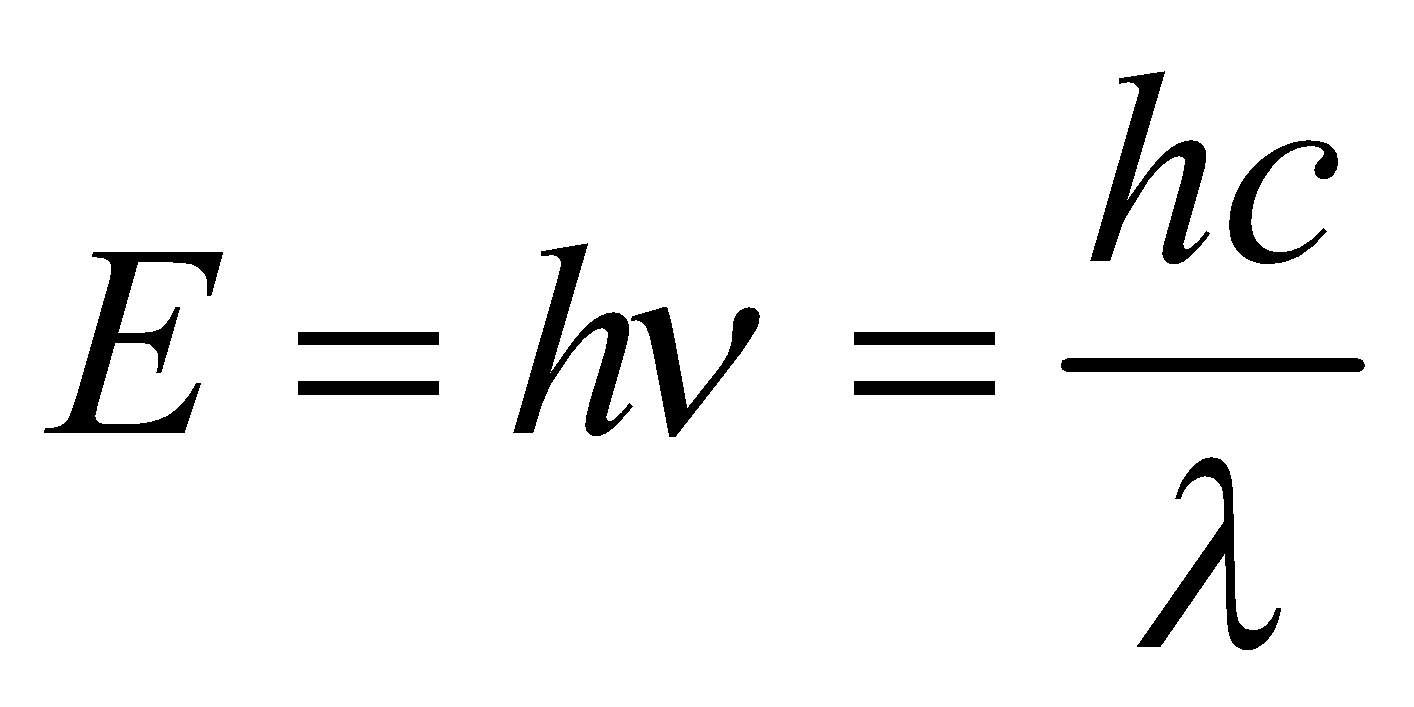 …(2)
…(2)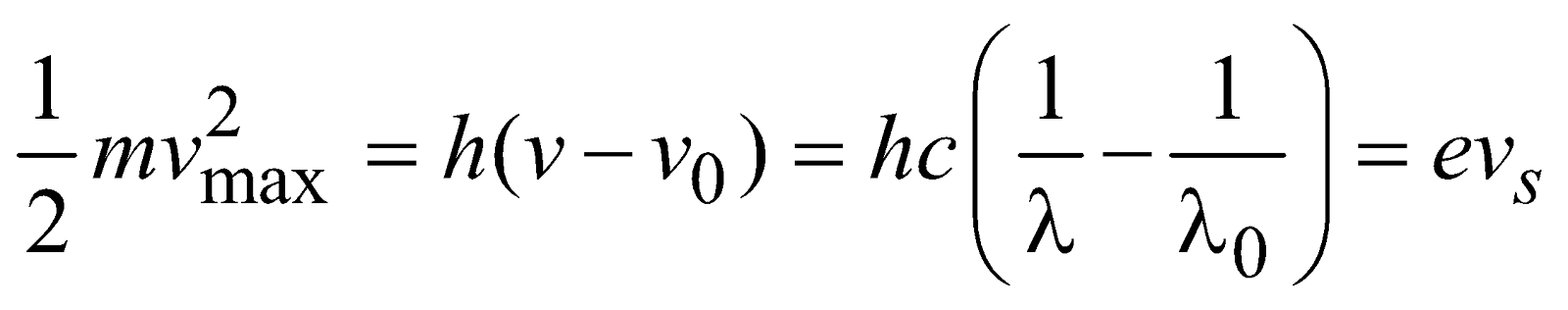
- It is clear from eq. (3) that if energy of photon is less than the work function of metallic surface, the electrons will never be ejected from the surface regardless of intensity of incident light.
- Kmax is independent of intensity of incident light, but it depends on the frequency of incident light i.e., Kmax ∝ ν (frequency of light).
- Electrons are emitted almost instantaneously consistent with particle view of light in which incident energy is concentrated in small packets (called photons) rather than over a large area (as in wave theory).
VARIOUS GRAPHS RELATED TO PHOTOELECTRIC EFFECT
- Mass spectrograph is an apparatus used to determine the mass or the specific charge (e/m) of positive ions. Examples are (a) Thomson mass spectrograph (b) Bain bridge mass spectrograph (c) Aston mass spectrograph (d) Dempster mass spectrograph etc.
- In photoelectric effect all photoelectrons do not have same kinetic energy. Their KE ranges from zero to Emax which depends on frequency of incident radiation and nature of cathode.
- The photoelectric effect takes place only when photons strike bound electrons because for free electrons energy and momentum conservations do not hold together.
- Cesium is the best photo sensitive material.
- Efficiency of photoemission

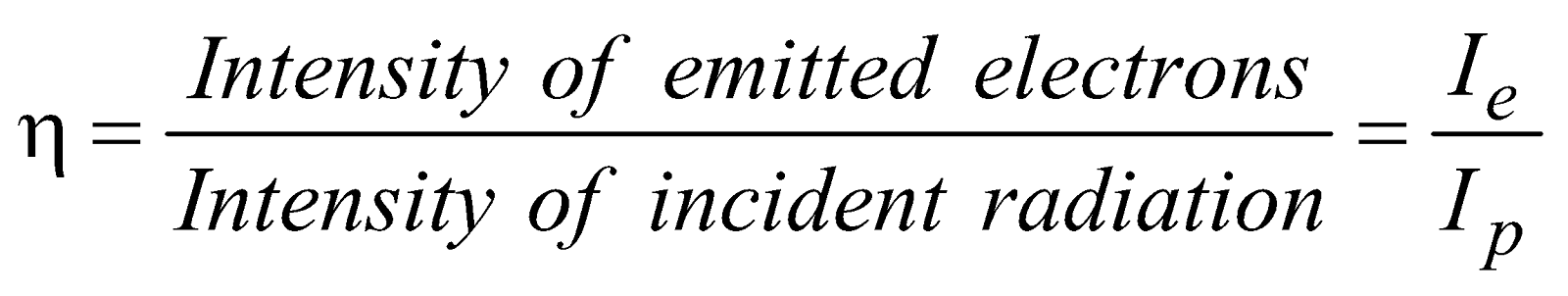
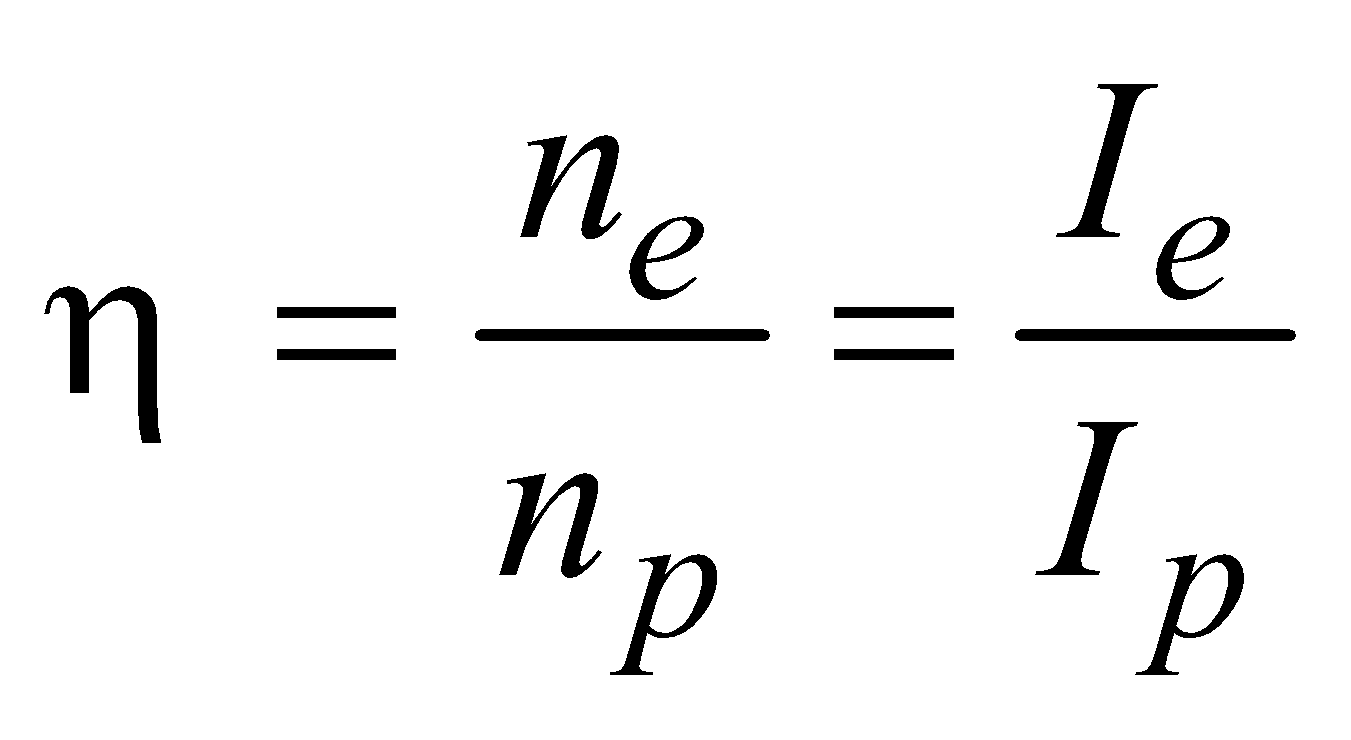
- Maximum velocity of emitted electrons
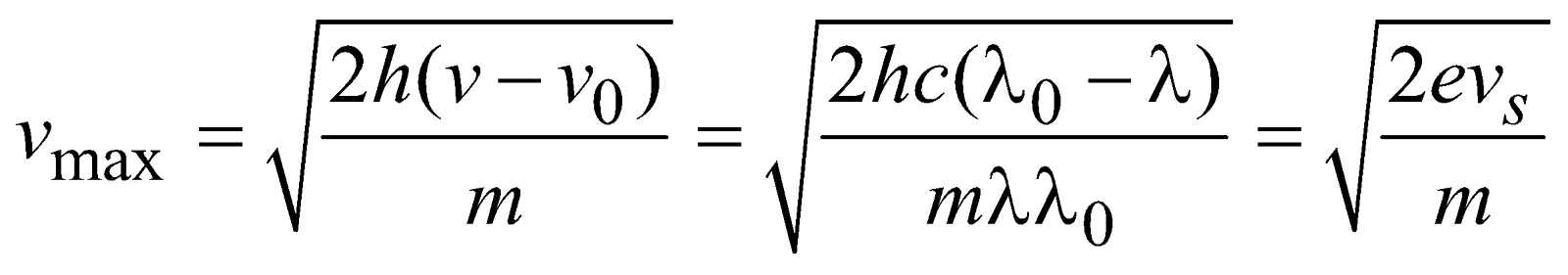
- Stopping potential
DE-BROGLIE EQUATION (DUAL NATURE OF MATTER)
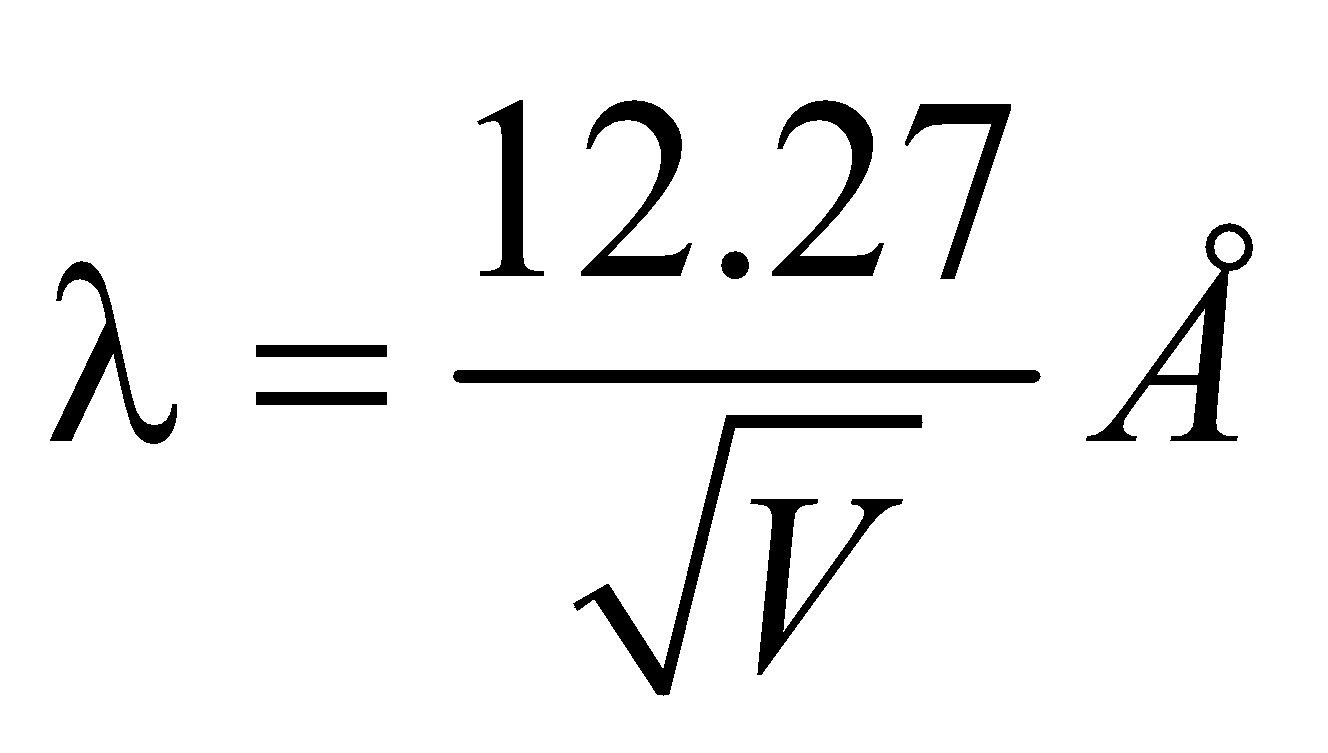
WAVELENGTH OF MATTER WAVES ASSOCIATED WITH ACCELERATED CHARGED PARTICLES
- For the charged particle
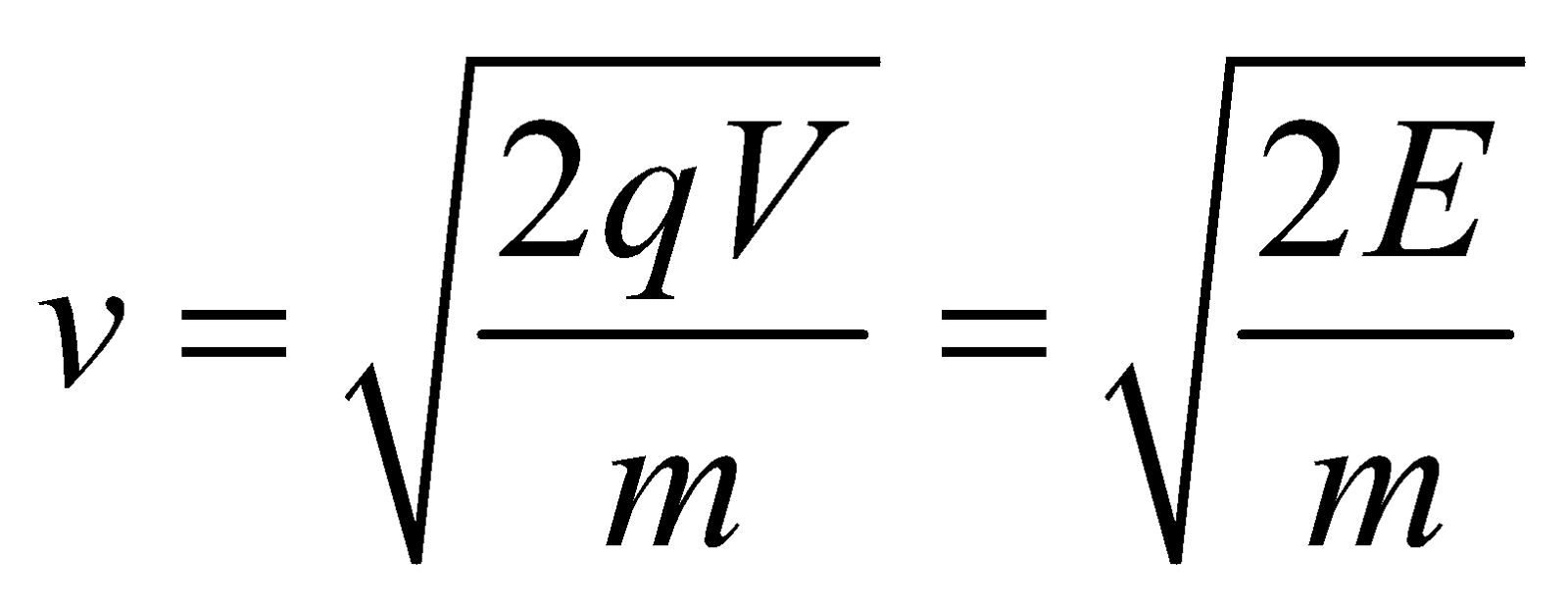
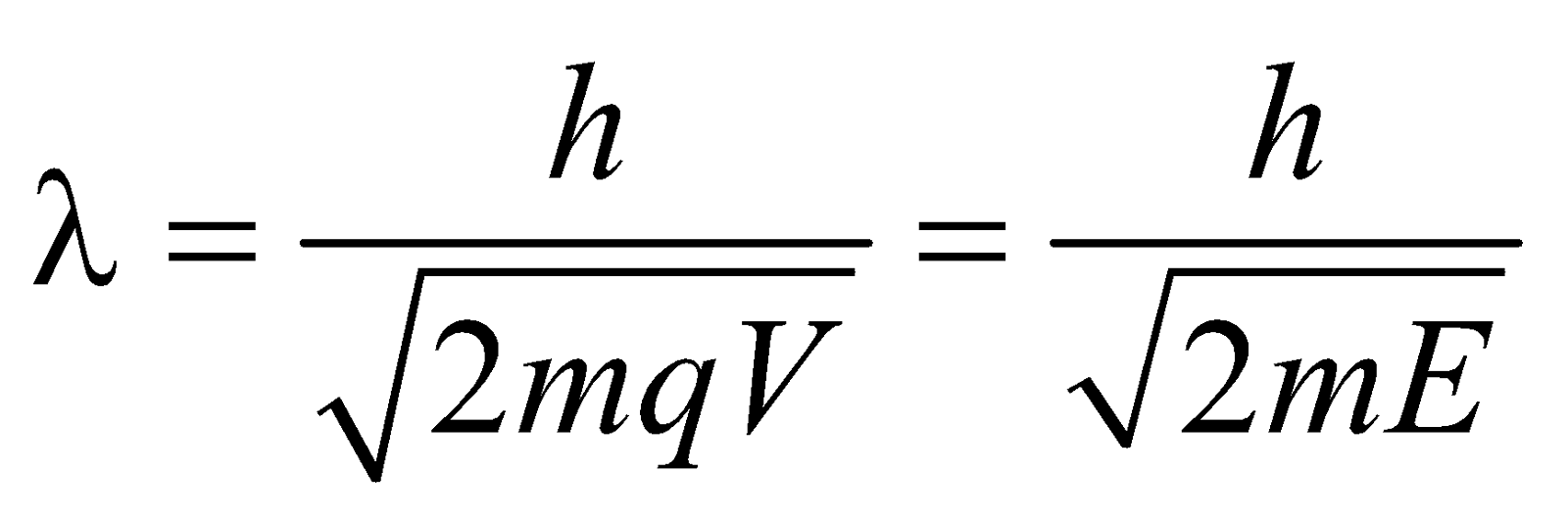
- For electron λe =
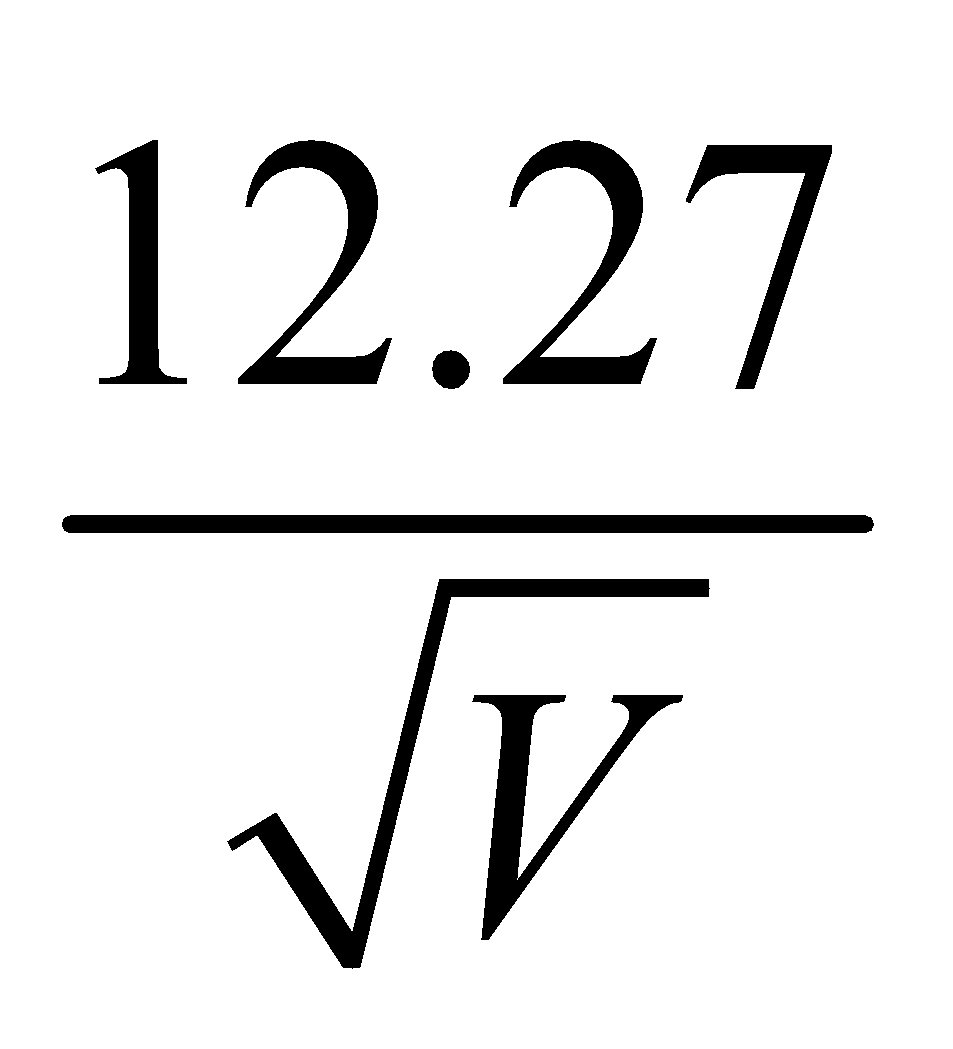 Å
Å - For proton λp =
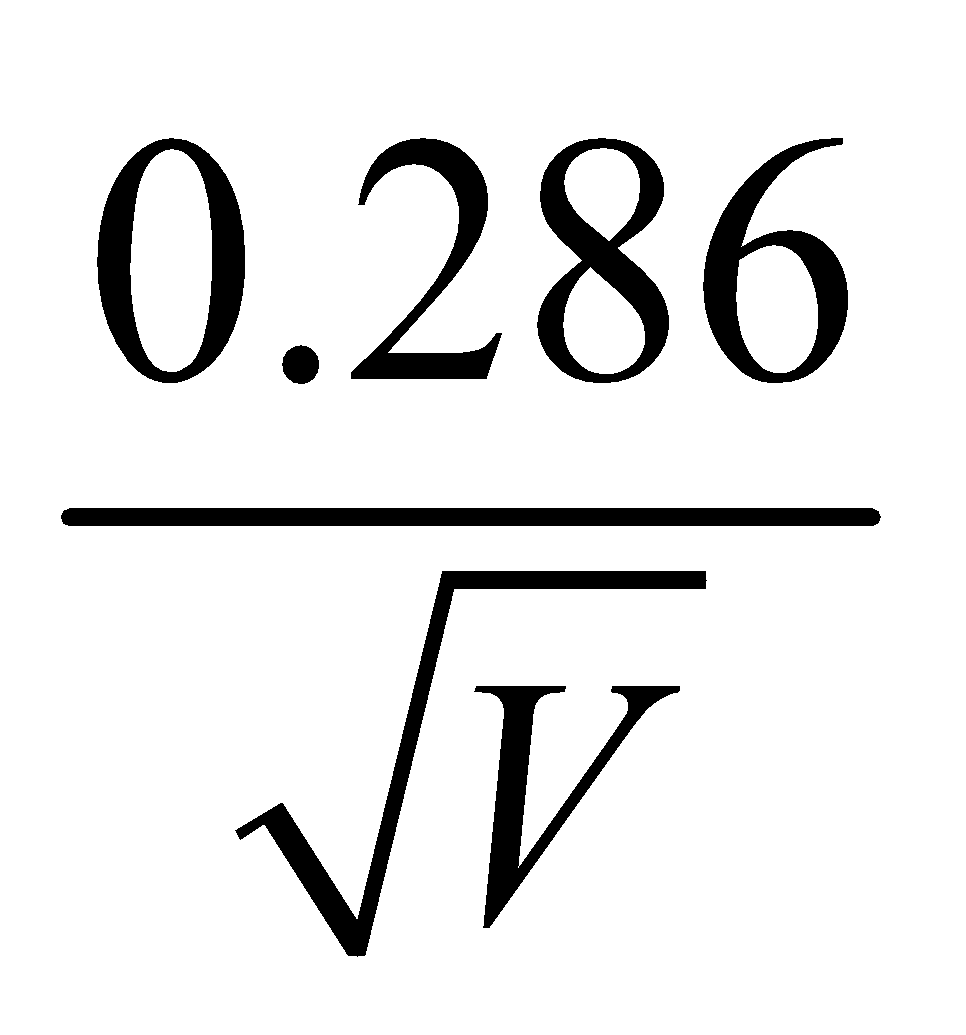 Å
Å - For alpha particle λα =
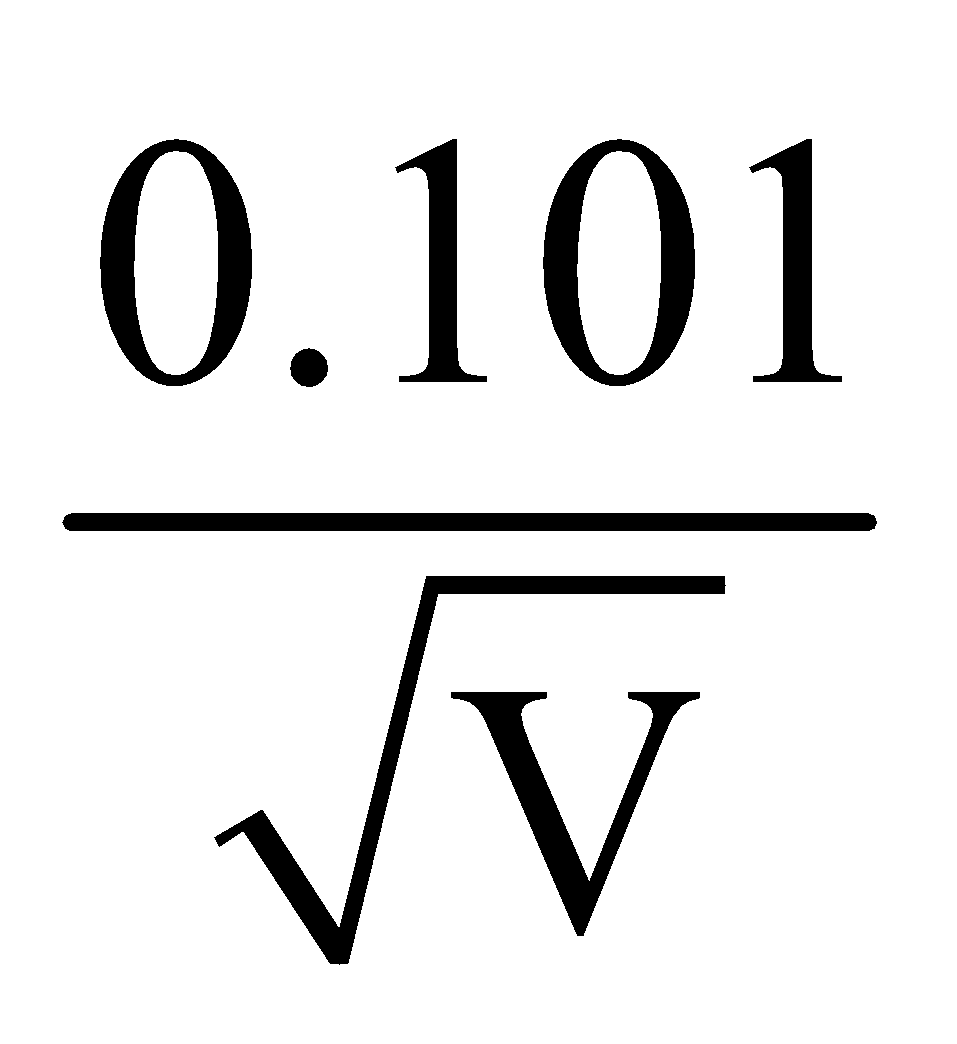 Å
Å - For deuteron λd =
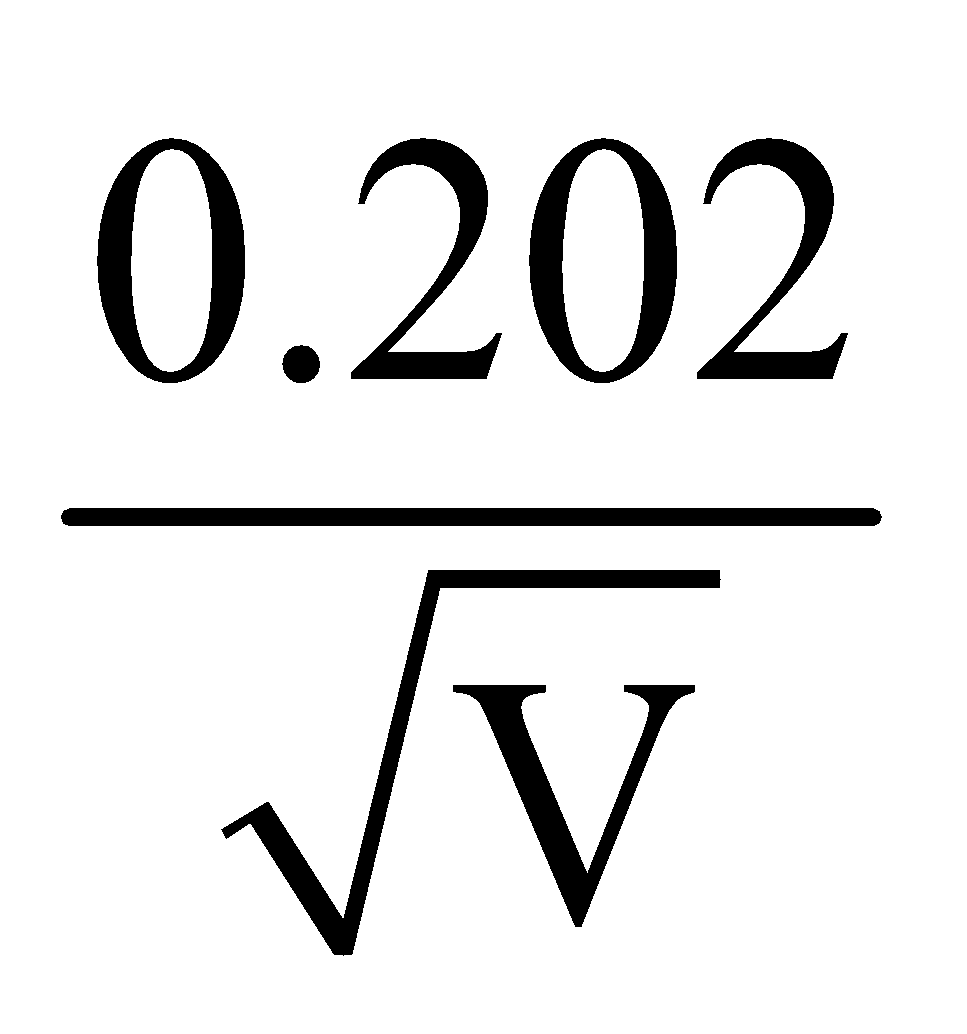 Å
Å
- For neutral particles (neutron, atom or molecule)
- If E is the energy of the particle, then,
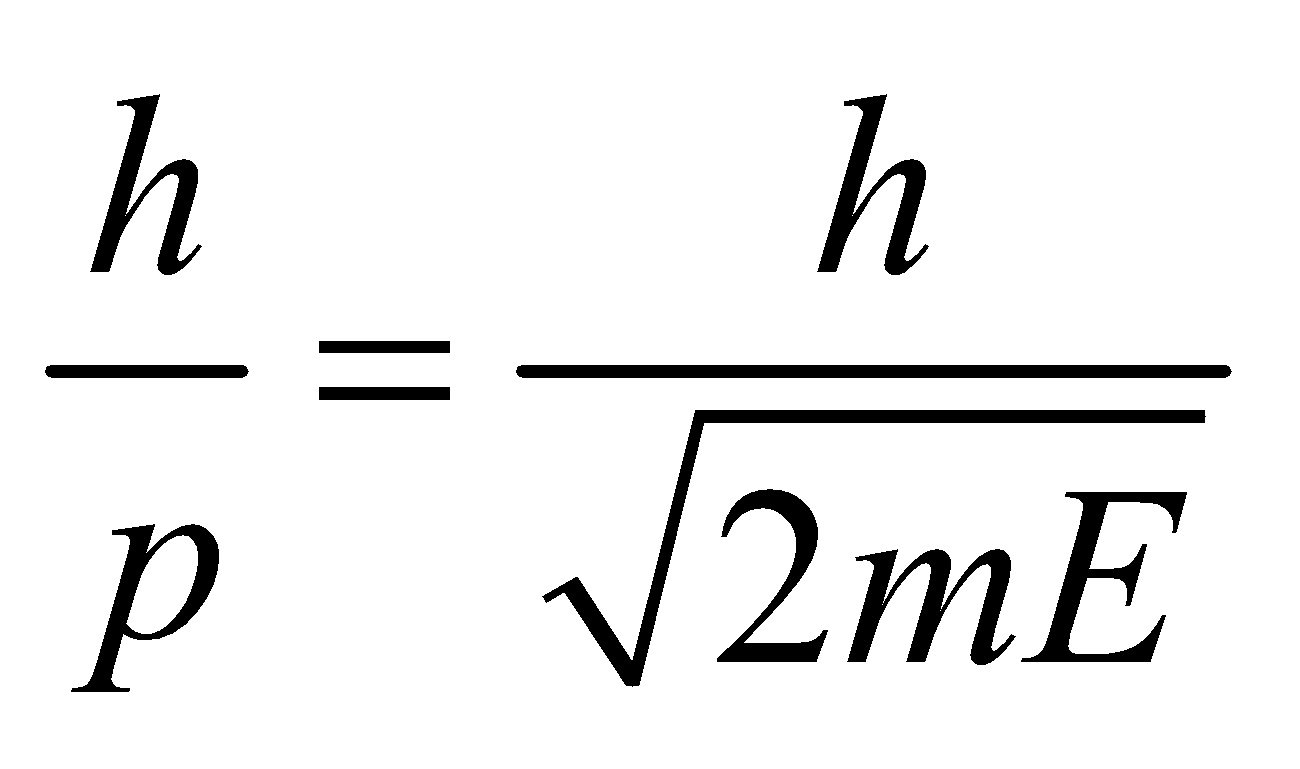
- If T is the temperature, then,
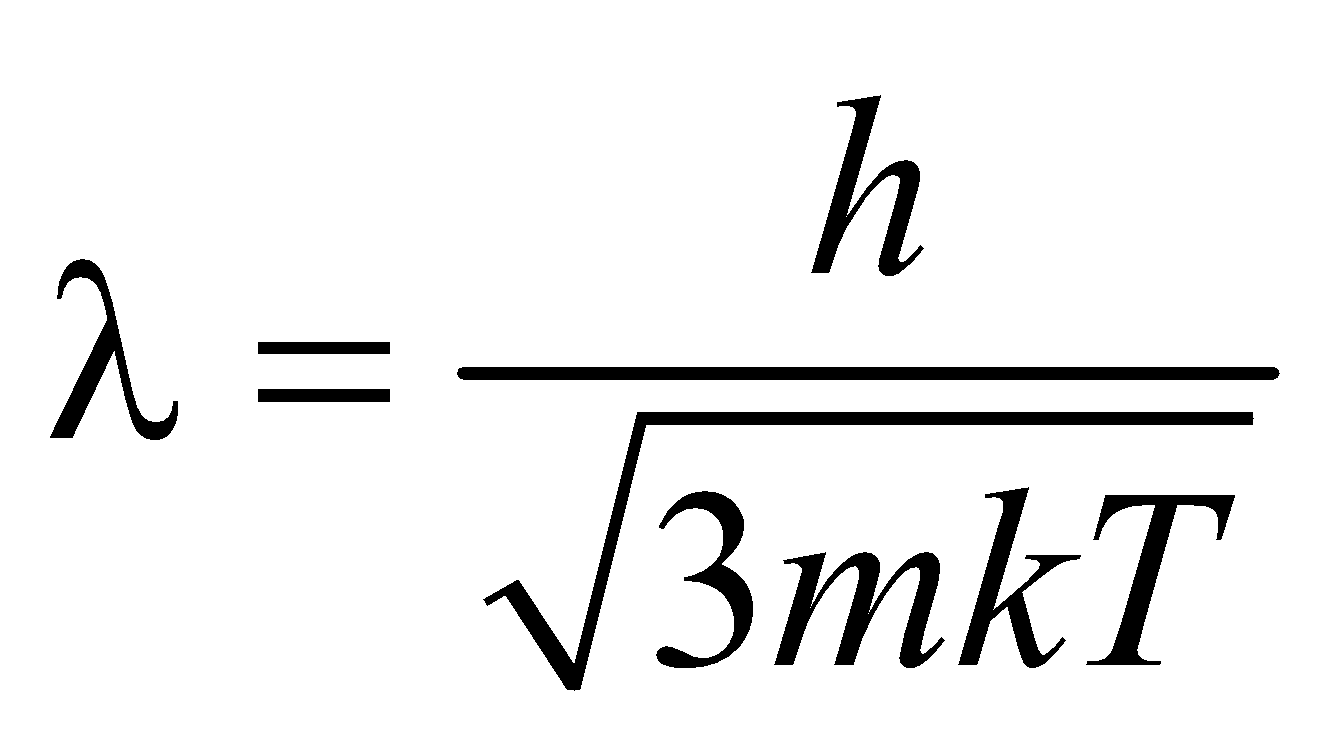
Dual nature of electron
DAVISSON-GERMER EXPERIMENT
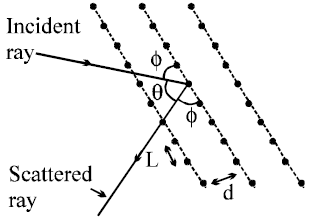
- According to Bohr’s quantum conditions :
- Matter waves associated with the electrons moving in an orbit are stationary waves.
- For the production of stationary waves in the orbit the circumference of the orbit should be integral multiple of wavelength of waves associated with the electron,
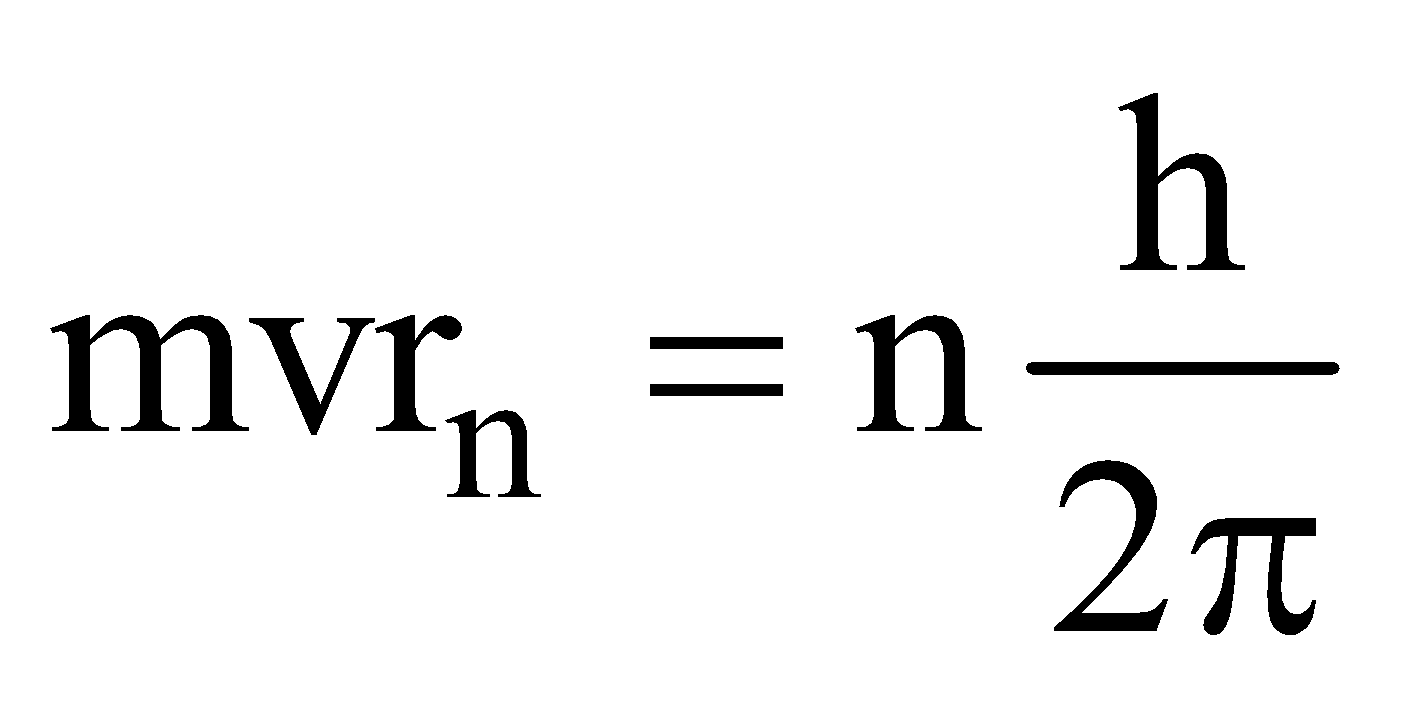
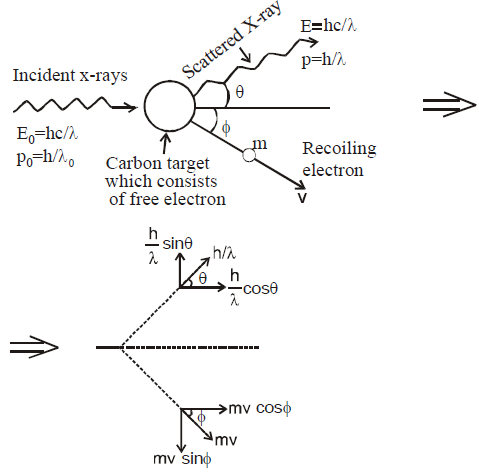
COMPTON EFFECT
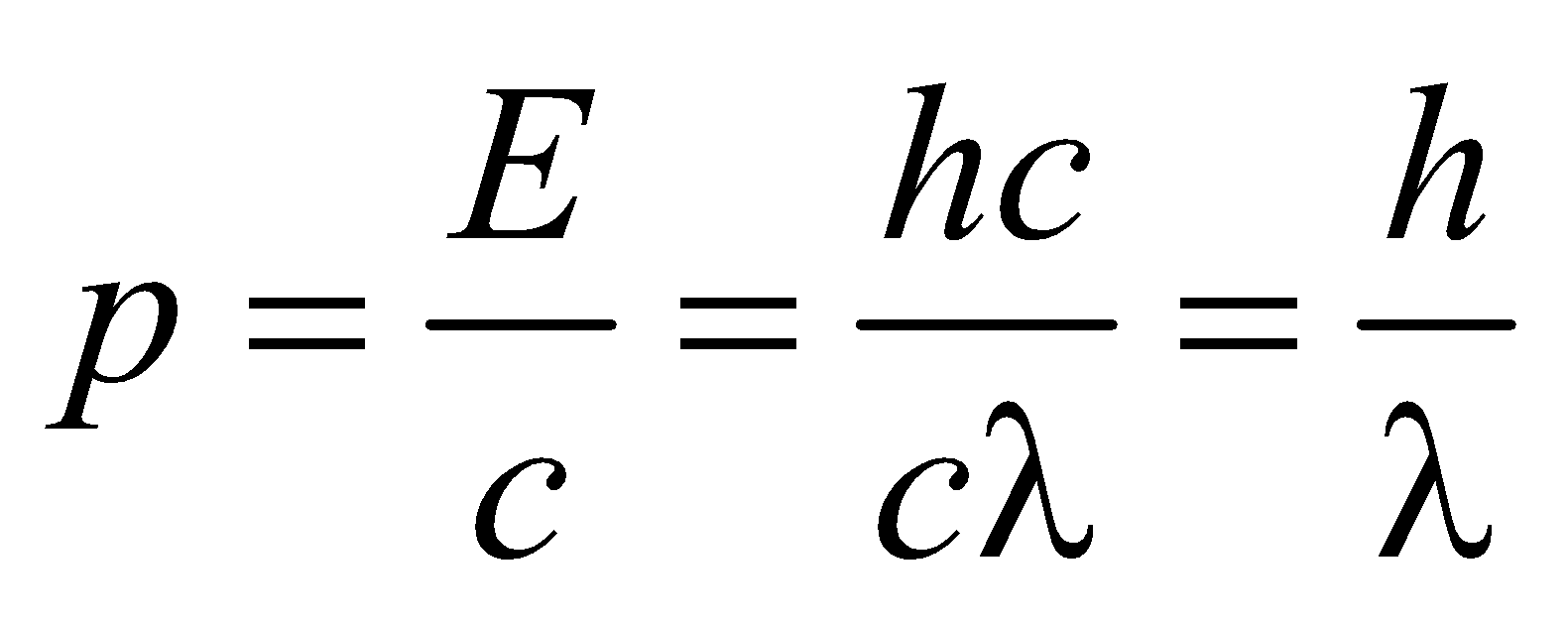 …(2)
…(2)
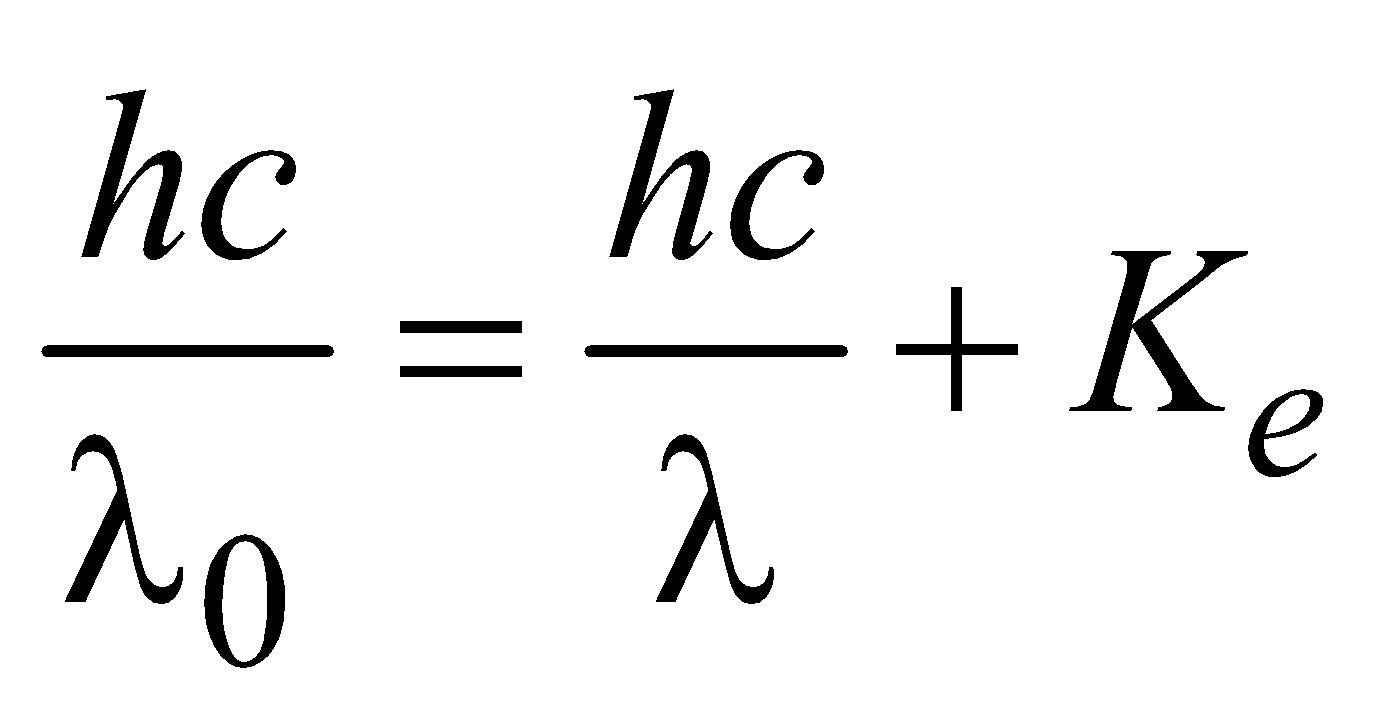 …(3)
…(3)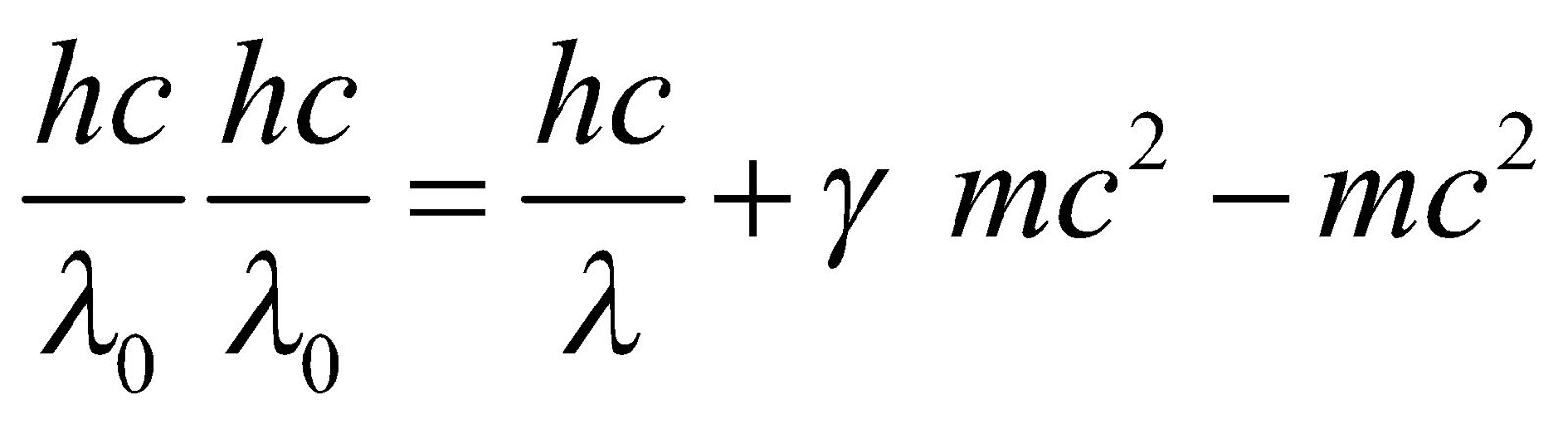 …(4)
…(4)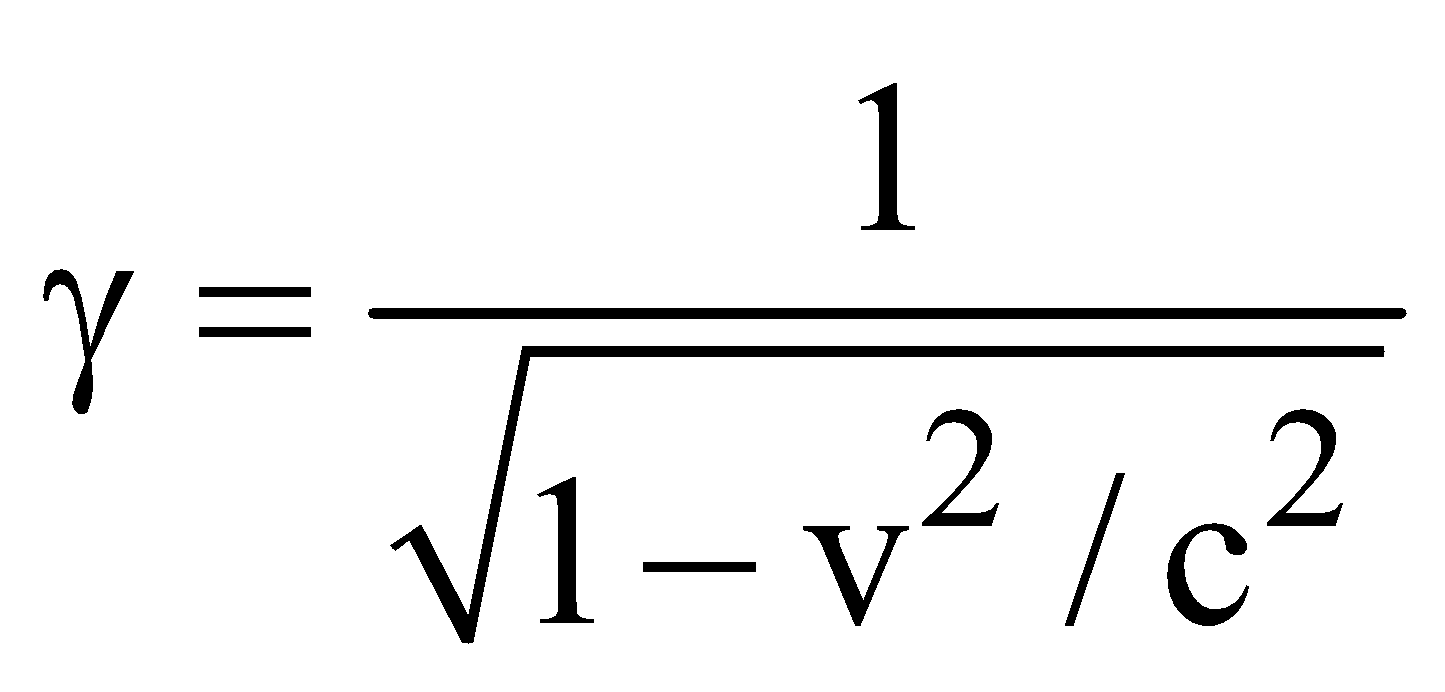
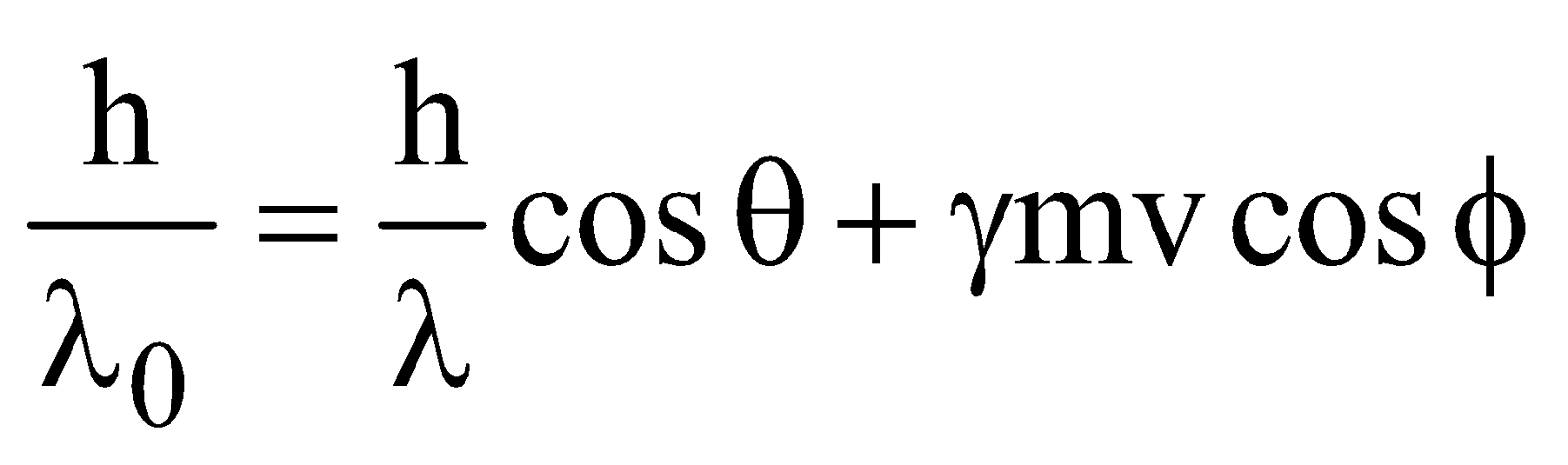 x-component …(5)
x-component …(5)
- The wave nature of light shows up in the phenomena of interference, diffraction and polarisation whereas photoelectric effect and Compton effect shows particle nature of light.
- The maximum kinetic energy of the photoelectrons varies linearly with the frequency of incident radiation but is independent of its intensity.
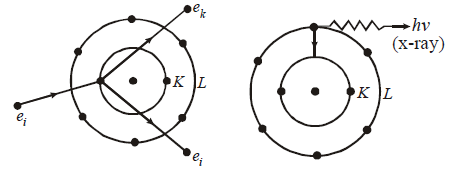
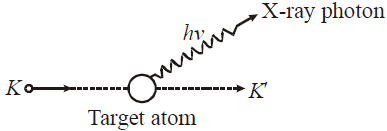
X-RAYS
- The X-rays were discovered by Prof. Roentgen, a German scientist in 1885. He was awarded Nobel Prize for this discovery in 1901. X-rays are electromagnetic waves.
- The modern apparatus for the production of X-rays was developed by Dr. Coolidge in 1913.
- X-rays are produced when fast moving electrons are suddenly stopped on a metal of high atomic number.
PROPERTIES OF X-RAYS
- They are not deflected by electric or magnetic field.
- They travel with the speed of light.
- There is no charge on X-rays.
- X-rays show both particle and wave nature.
- They are invisible.
CONTINUOUS AND CHARACTERISTIC X-RAYS
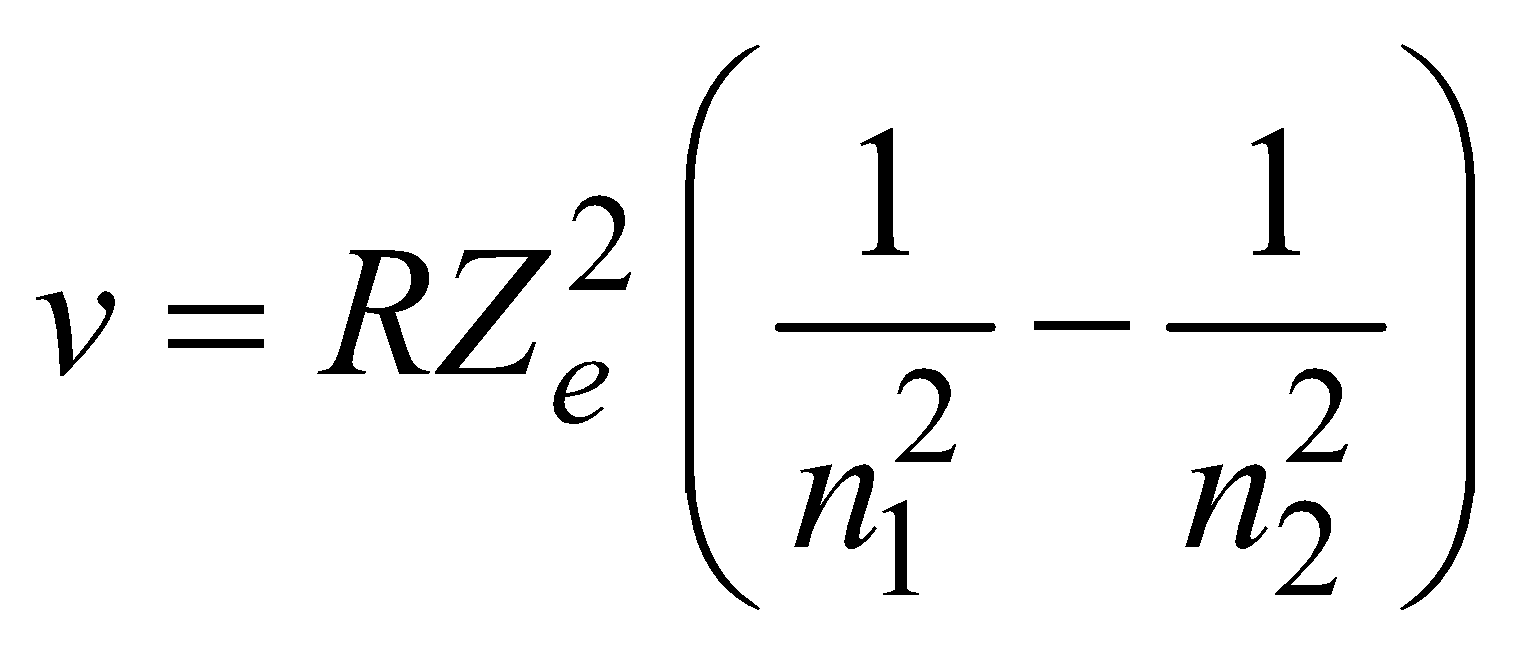
where R is constant and Ze is effective atomic number. Generally Ze is taken to be equal to Z – σ, where Z is proton number or atomic number of the element and σ is called the screening constant. Due to the presence of the other electrons. The charge of the nucleus as seen by the electron will be different in different shells.
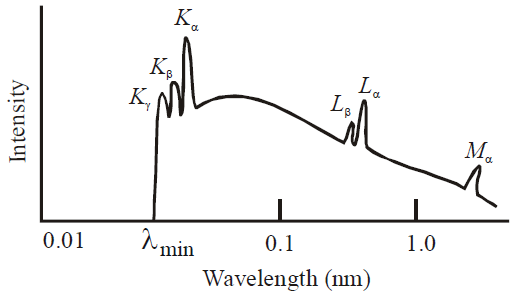
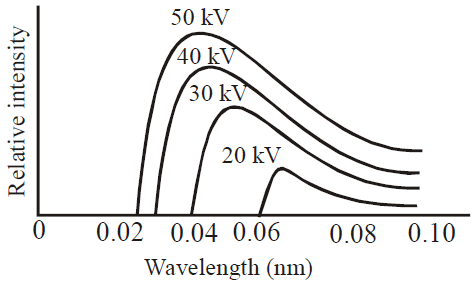
WAVELENGTH OF X-RAYS (DUANE HUNT LAW)
- When an electron is accelerated through a potential difference V then the energy acquired by electron
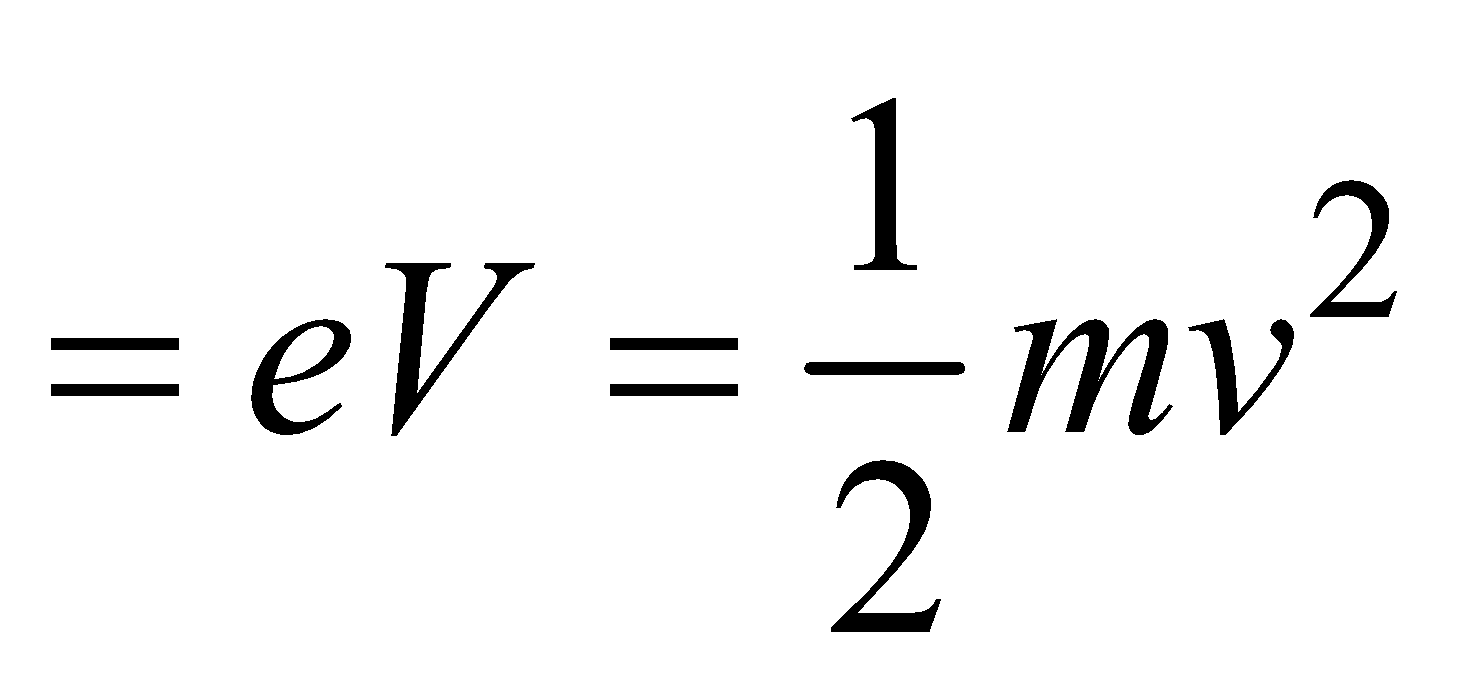
- When these high energy electrons fall on target T of high atomic number, then X-rays are produced, whose wavelength is given by
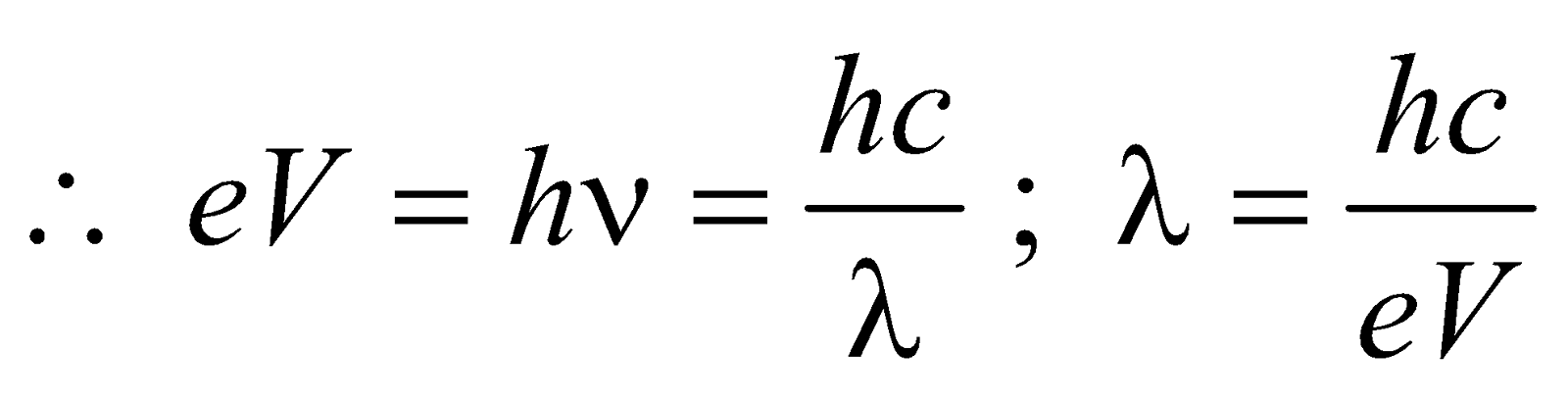
- The energy of X-rays of wavelength λ is
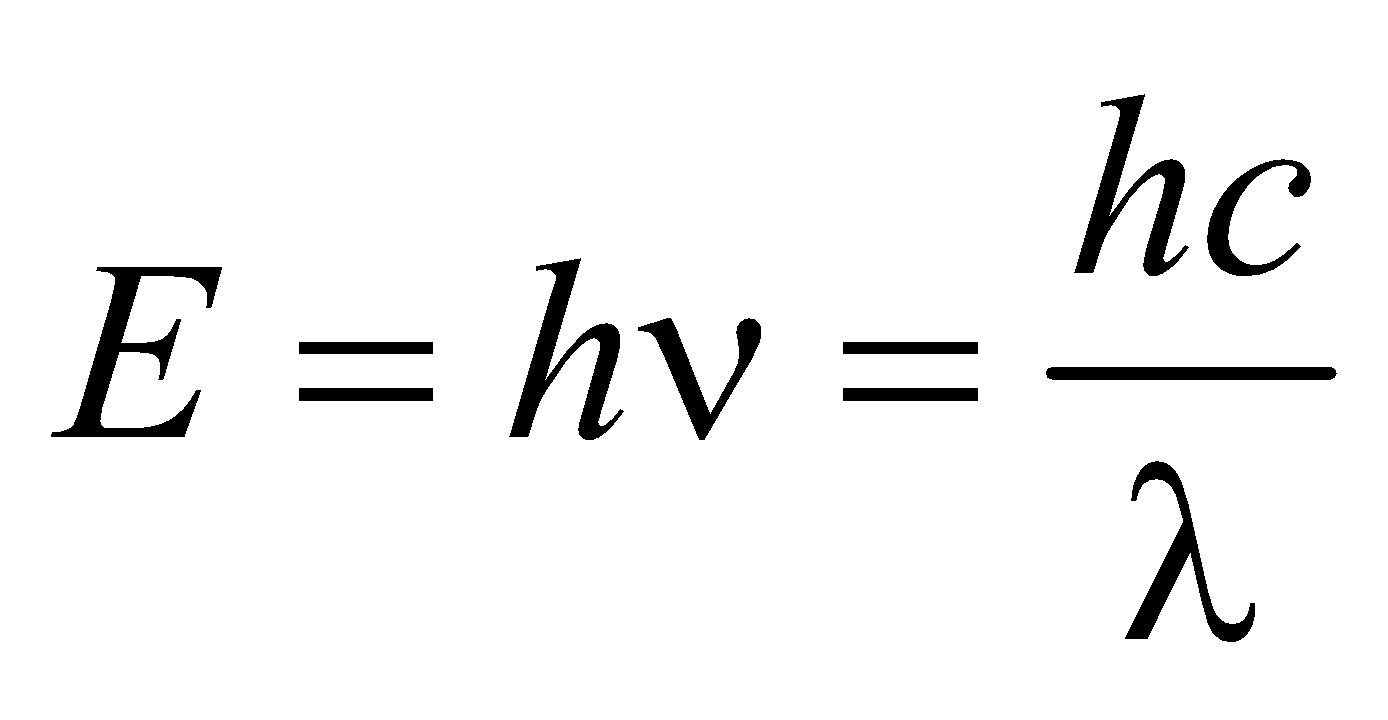
- The shortest wavelength of X-rays emitted is
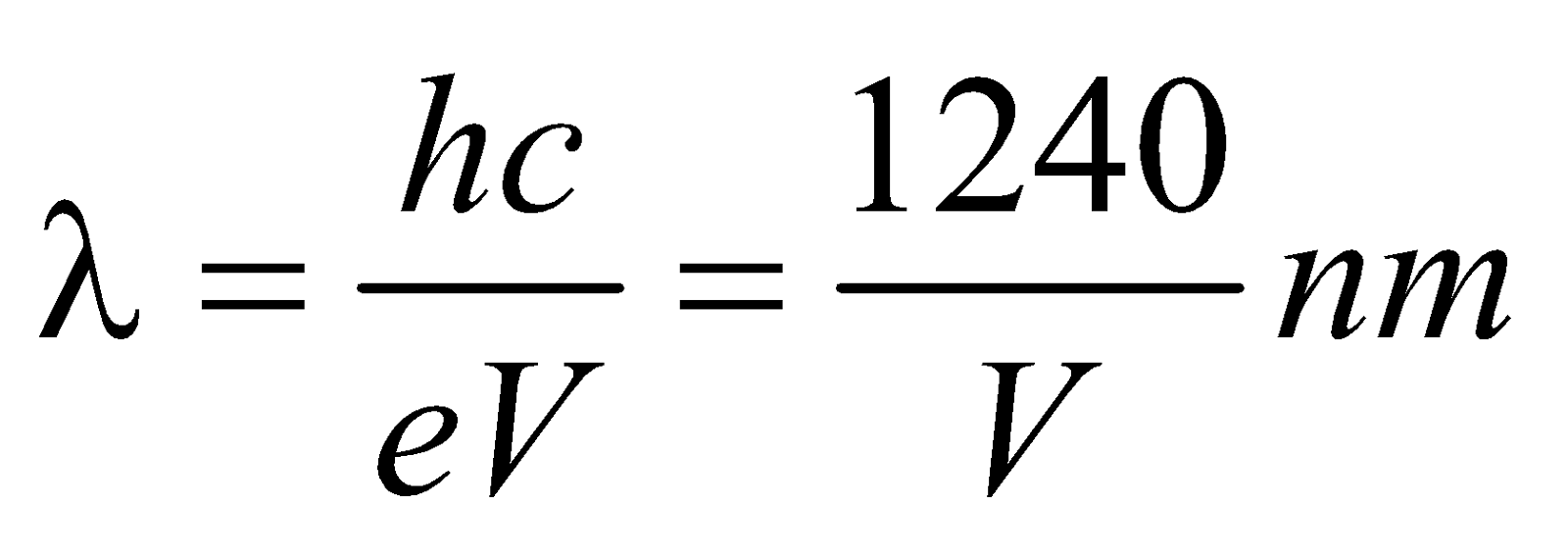 i.e.
i.e. 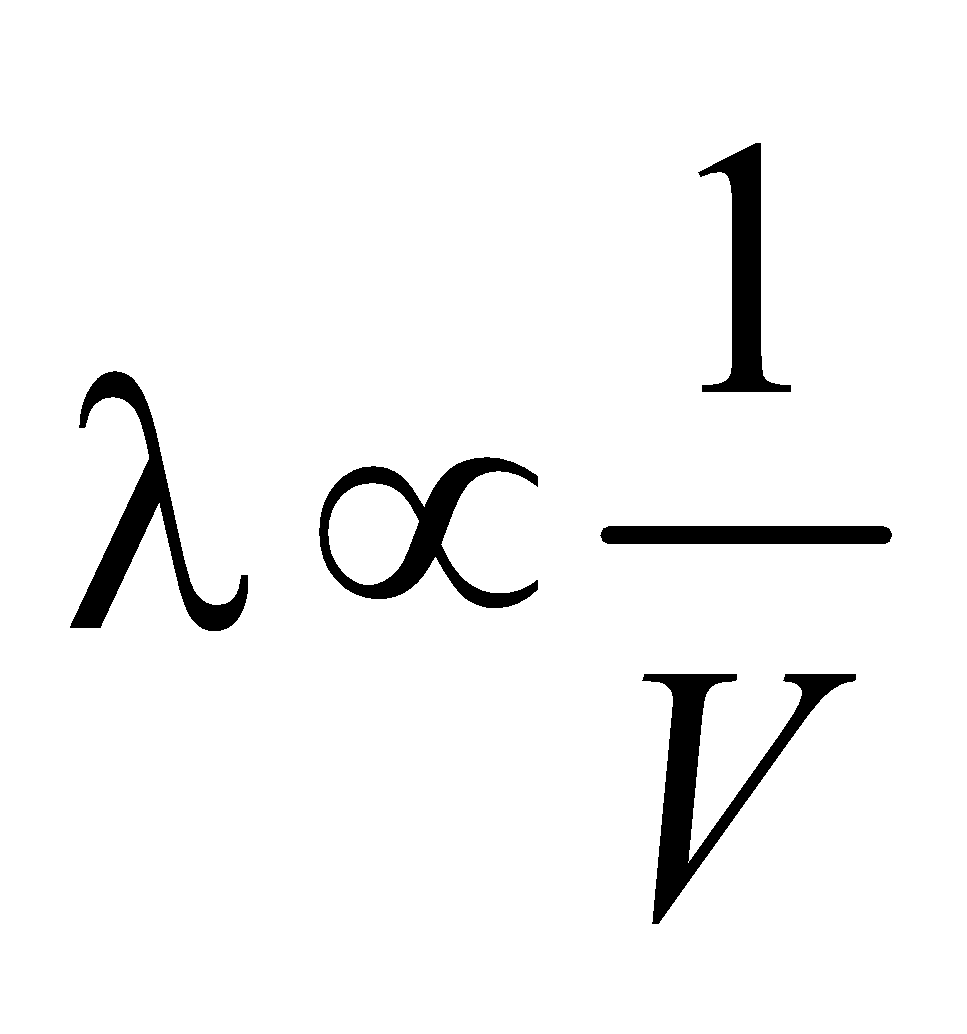
TYPES OF X-RAYS
- Hard X-rays : The X-rays of high frequency or low wavelength are said to be hard X-rays. They have higher penetrating power.
- Soft X-rays : The X-rays of longer wavelength are called soft X-rays.
MOSELEY’S LAW
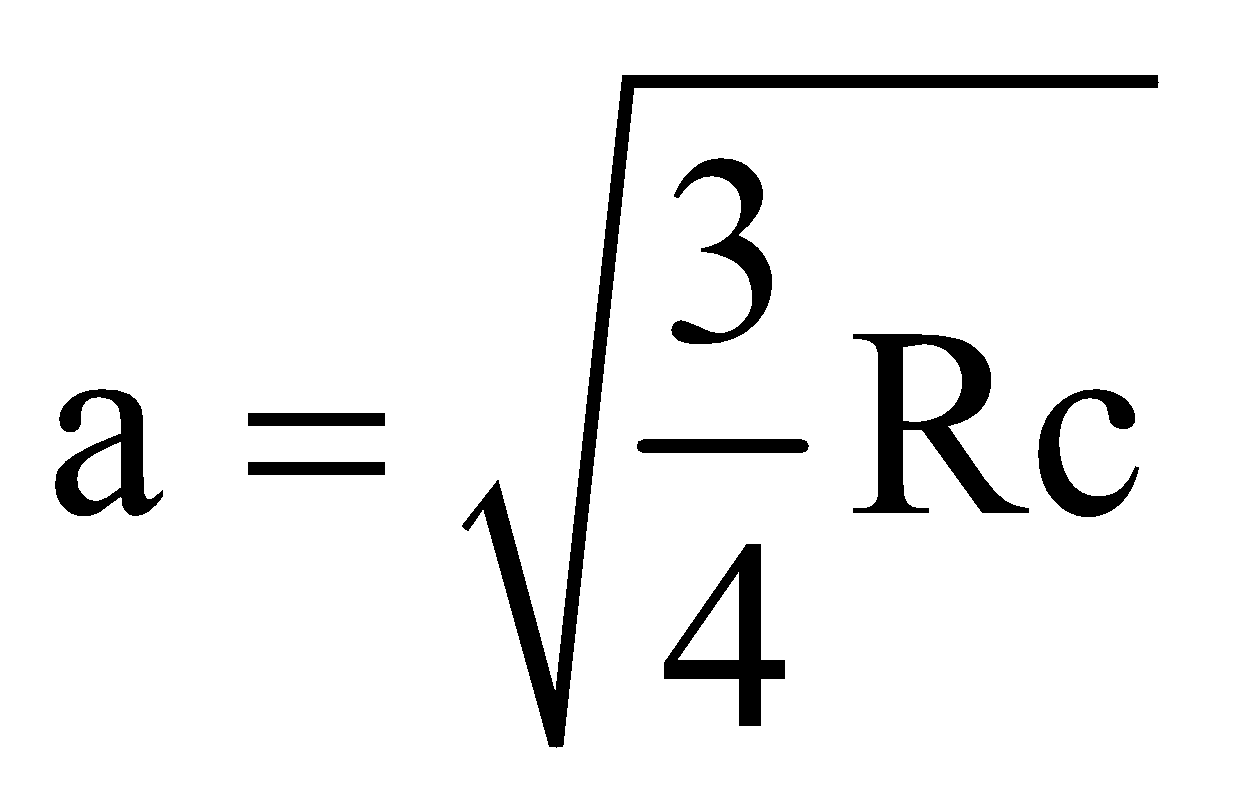 and b = 1
and b = 1ABSORPTION OF X-RAYS
- X-rays are absorbed by the materials according to the relation I = I0 e–μx, where μ is absorption coefficient and x is the thickness of the material. Here I is the intensity after penetrating the material through distance x and I0 is the initial intensity of the X-rays.
- The coefficient of absorption (μ) of the material is given by
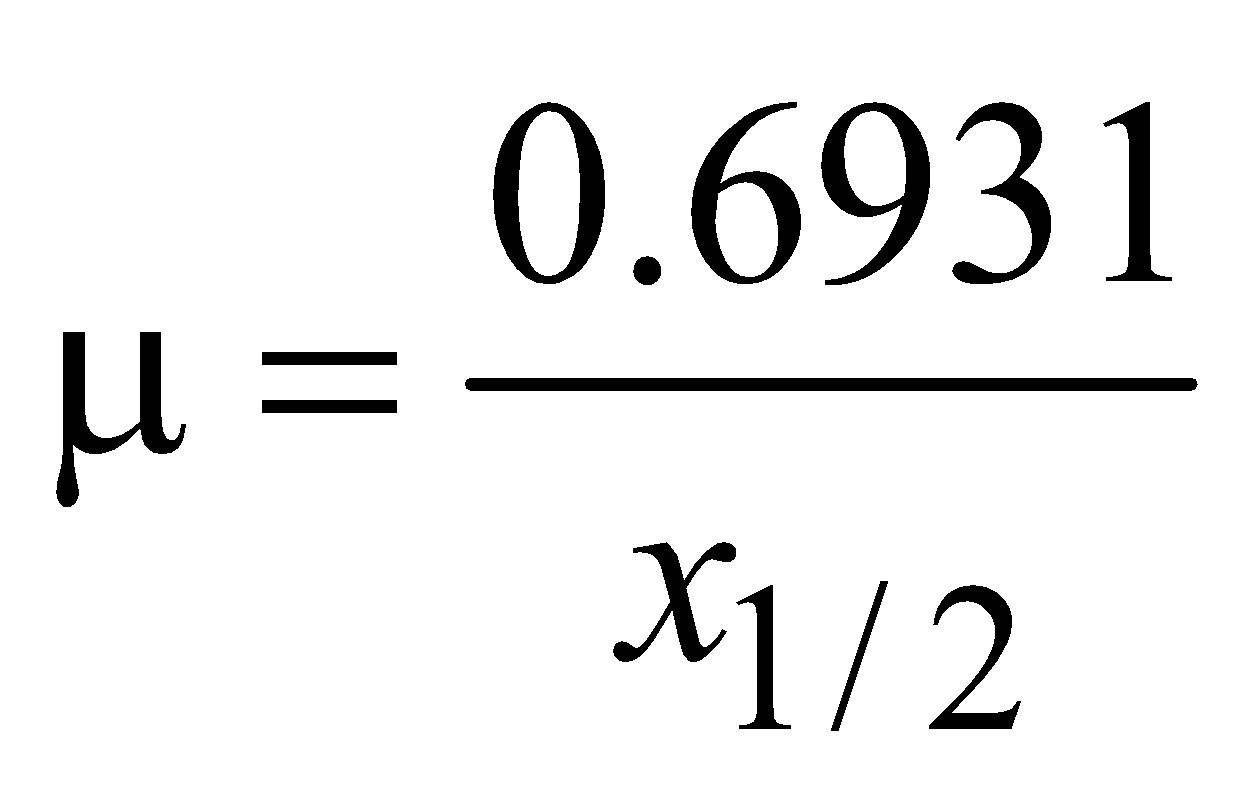
where x1/2 is the distance after traversing which the intensity of X-rays is reduced to half. - Absorption coefficient depends on the nature of material and wavelength of X-rays i.e. μ = cZ4 λ3.
- When quinine sulphate is illuminated with ultraviolet or violet light it gives out blue light. The fluorescence of barium sulphate as well as uranium oxide gives out green light when illuminated with ultraviolet or violet light.
- The house hold tubes are painted from inside with magnesium tungstate or zinc-beryllium silicate. They are fluorescent materials. The ultraviolet light generated inside the tube falls on the walls, where magnesium tungstate gives blue light and zinc beryllium silicate gives yellow orange light. The mixture of the two produces white light. If the inner side of the tube is painted with cadmium borate it gives fluorescence of pink light and when painted with zinc silicate, it gives fluorescence of green light.
- The fluorescence occurs as long as the material is illuminated.
- The stopping potential (and hence the maximum kinetic energy of emitted electrons) is independent of the intensity of light but that the saturation current (and hence the number of emitted photoelectrons) is proportional to the intensity.
- Photoelectric effect doesn’t take place below the threshold frequency for the photo metal used.
- In Compton effect, the change in wavelength is independent of incident photon as well as of the nature of the scatterer, but depends only on the angle of scattering (θ).
- The quantity
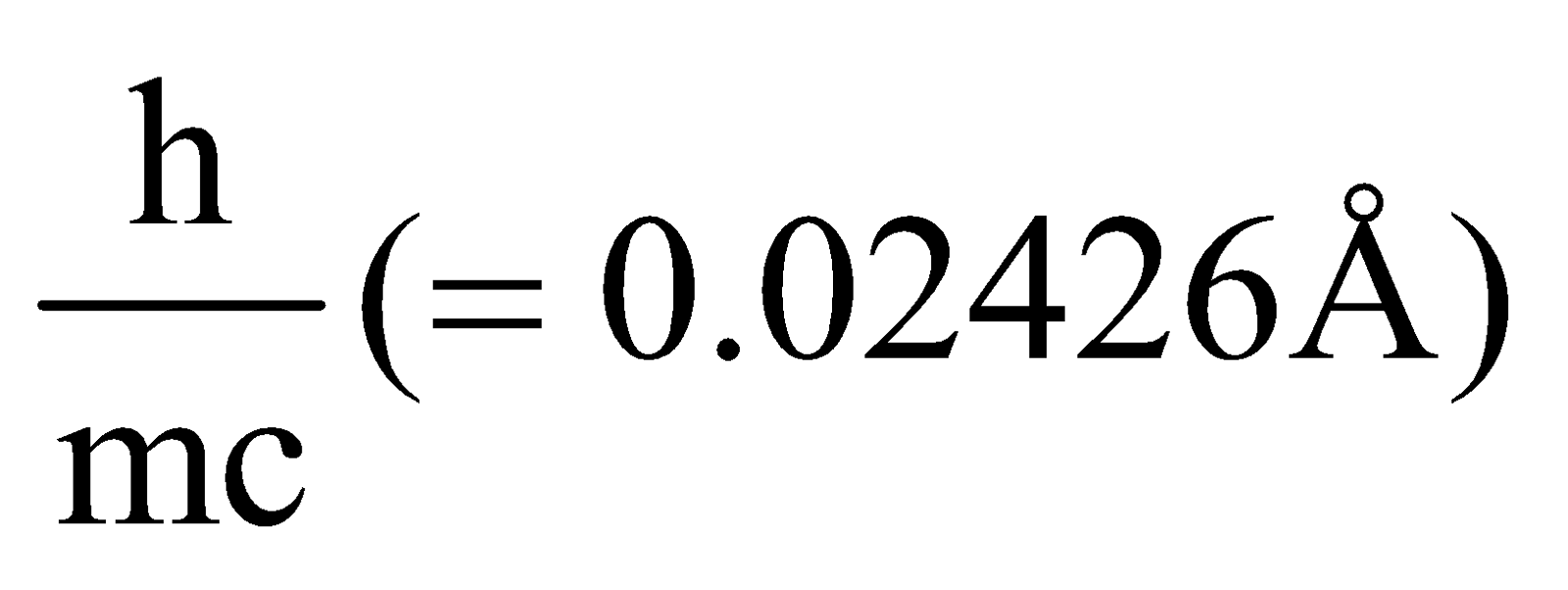 is called Compton wavelength.
is called Compton wavelength. - The maximum wavelength change possible in Compton effect is 0.05Å.
- Compton effect can’t be observed for visible light rays.
- In Compton effect, the direction of recoil electron is given by
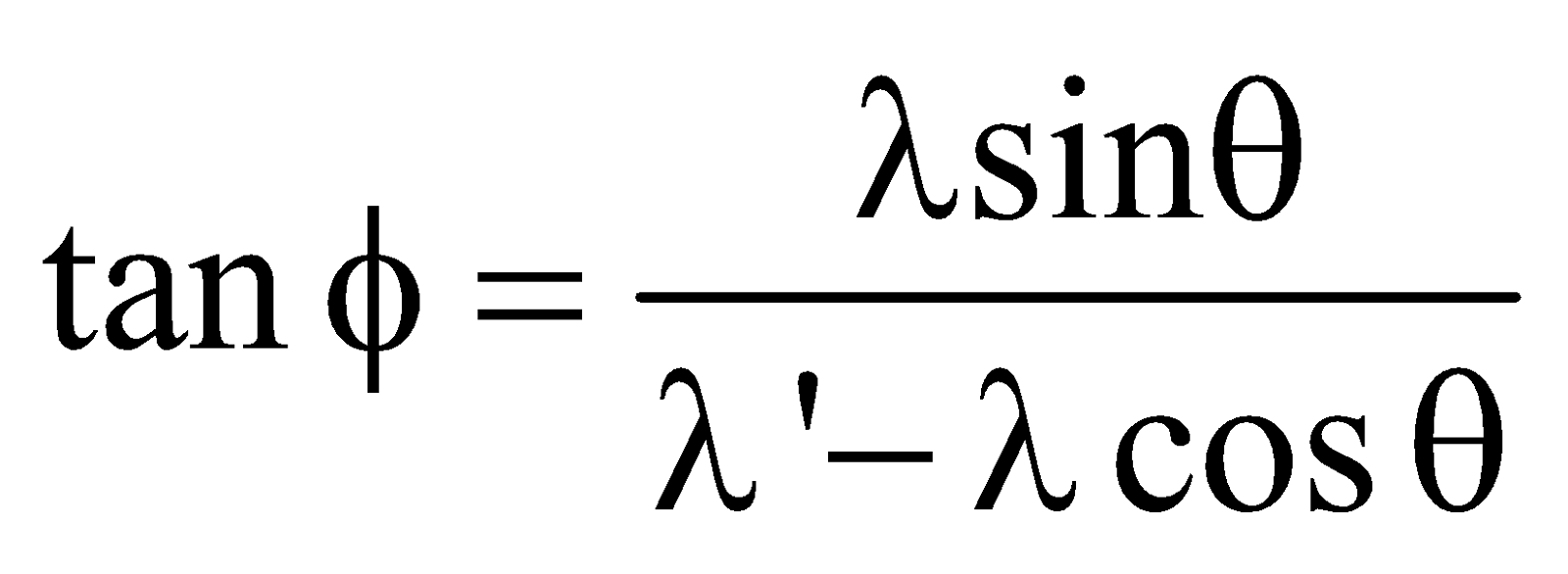
- The kinetic energy of recoil electron is given by
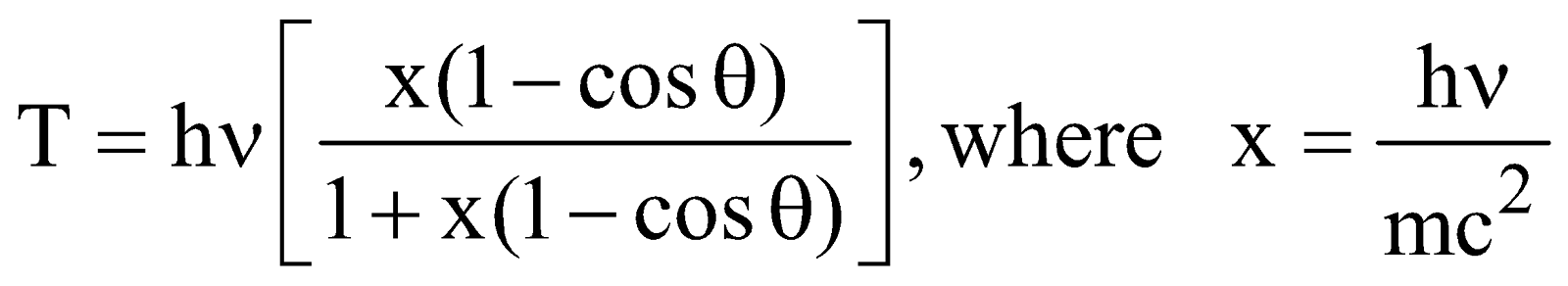
- de-Broglie wavelength of a particle of K.E., Ek is given by
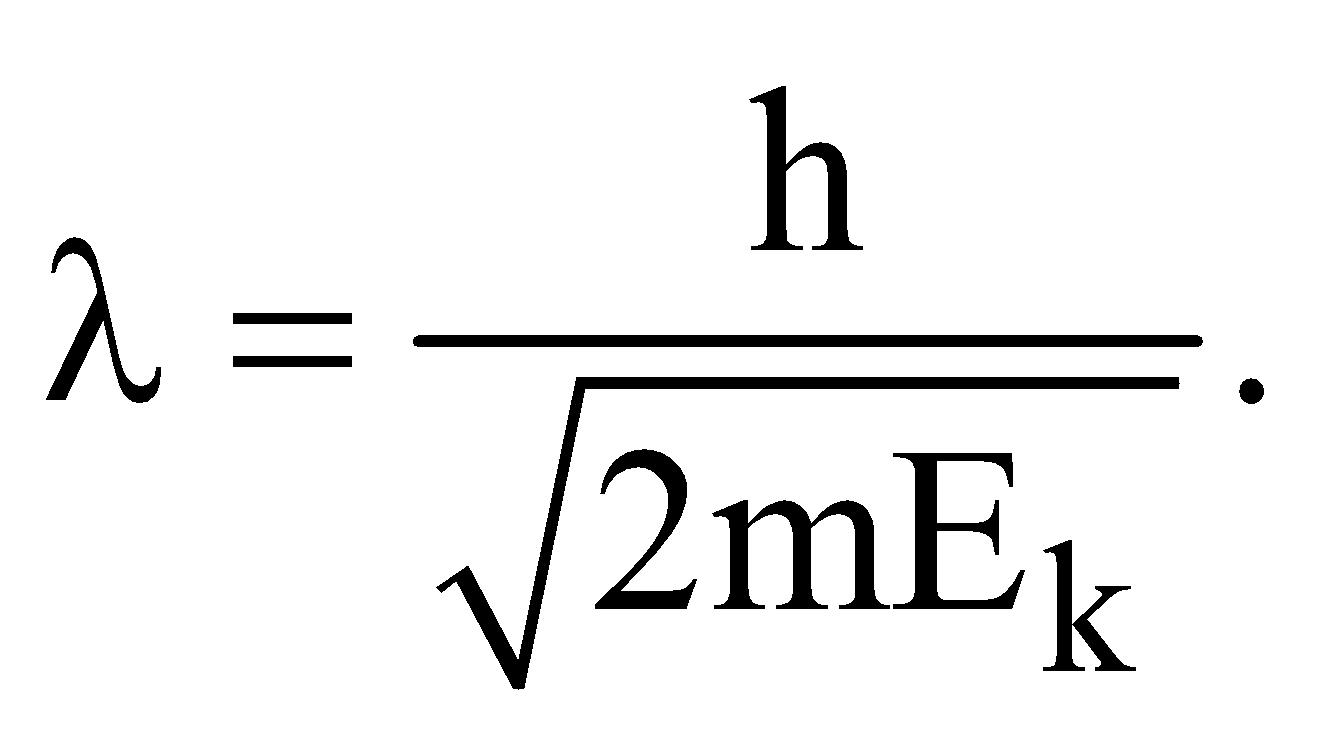
- de-Broglie wavelength for a charged particle with charge q and accelerated through a potential difference V is given by
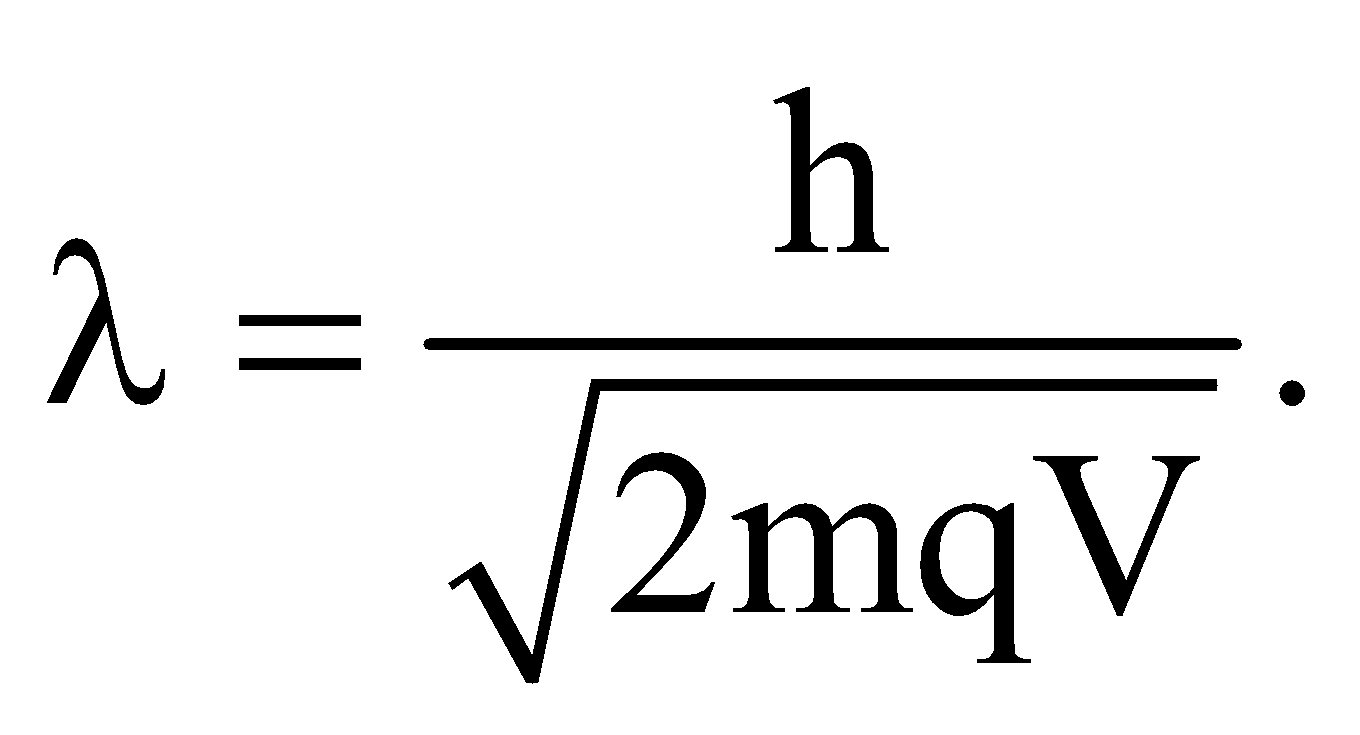
- de-Broglie wavelength of a material particle at temperature T is given by
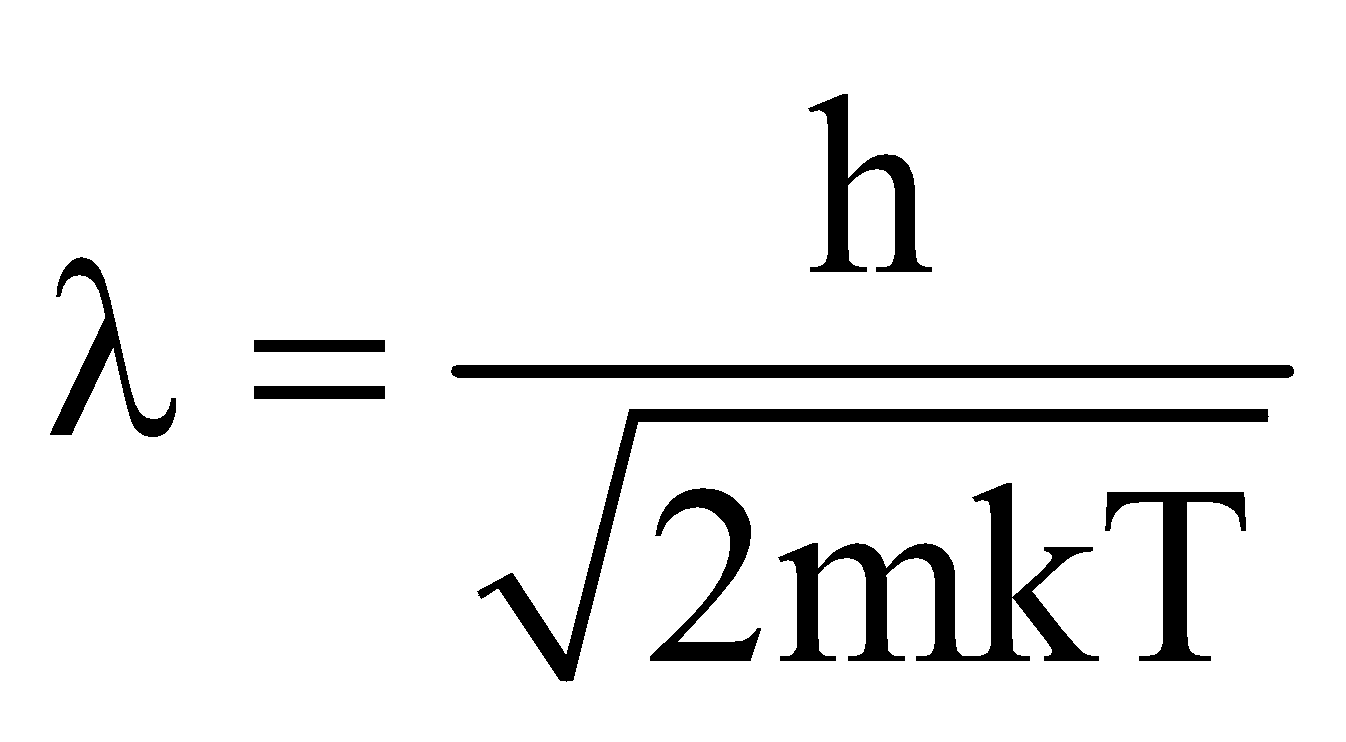 , where k is Boltzmann’s constant.
, where k is Boltzmann’s constant.APPLICATION OF X-RAYS
- Scientific applications : The diffraction of X-rays at crystals opened new dimension to X-rays crystallography. Various diffraction patterns are used to determine internal structure of crystals. The spacing and dispositions of atoms of a crystal can be precisely determined by using Bragg’s law : nλ = 2d sin θ.
- Industrial applications : Since X-rays can penetrate through various materials, they are used in industry to detect defects in metallic structures in big machines, railway tracks and bridges. X-rays are used to analyse the composition of alloys and pearls.
- In radiotherapy : X-rays can cause damage to the tissues of body (cells are ionized and molecules are broken). So X-rays damages the malignant growths like cancer and tumours which are dangerous to life, when is used in proper and controlled intensities.
- In medicine and surgery : X-rays are absorbed more in heavy elements than the lighter ones. Since bones (containing calcium and phosphorus) absorb more X-rays than the surrounding tissues (containing light elements like H, C, O), their shadow is casted on the photographic plate. So the cracks or fracture in bones can be easily located. Similarly intestine and digestive system abnormalities are also detected by X-rays.
Dual Nature of Electron
(1) In 1924, the French physicist, Louis de Broglie suggested that if light has electron, behaves both as a material particle and as a wave.
(2) This presented a new wave mechanical theory of matter. According to this theory, small particles like electrons when in motion possess wave properties.
(3) According to de-broglie, the wavelength associated with a particle of mass m, moving with velocity v is given by the relation λ = h/mv where h = Planck’s constant.
(4) This can be derived as follows according to Planck’s equation, E = hv = hc /λ ∴ v=c/λ(energy of photon (on the basis of Einstein’s mass energy relationship) E = mc2,
Equating both hc/λ = mc2 or λ = h/mc which is same as de-Broglie relation. (∴ mc = p)
(5) This was experimentally verified by Davisson and Germer by observing diffraction effects with an electron beam. Let the electron is accelerated with a potential of V than the Kinetic energy is
\(\frac{1}{2}mv^2=eV\)
or
\(m^2v^2=2meV\)
or
\(mv=\sqrt{2meV}=p\) momentum
\(\therefore \lambda =\frac{h}{p}=\frac{h}{\sqrt{2meV}}\)
(6) If Bohr’s theory is associated with de-Broglie’s equation then wavelength of an electron can be determined in bohr’s orbit and relate it with circumference and multiply with a whole number 2πr = nλ or λ = (2πr/2π) From de-Broglie equation, λ = (h/mv).
Thus h/mv = (2πr/n) or mvr = (nh/2π)
(7) The de-Broglie equation is applicable to all material objects but it has significance only in case of microscopic particles. Since, we come across macroscopic objects in our everyday life, de-broglie relationship has no significance in everyday life.
Heisenberg uncertainty principle
The Heisenberg uncertainty principle applied to position and momentum states that it is not possible to measure simultaneously the position and momentum of a particle with indefinite precision. This has nothing to do with imperfect measuring devices or experimental errors. It represents a fundamental property of nature. The uncertainty \( \Delta x \) in position and the uncertainty \( \Delta p \) in momentum are related by:
\(\Delta x\Delta p\geq \frac{h}{4\pi}\) where \(h\) is Planck’s constant.
This says that making momentum as accurate as possible makes position inaccurate, whereas accuracy in position results in inaccuracy in momentum. In particular, if one is made zero, the other has to be infinite.
Electron in a box’
As an application of the uncertainty principle, consider an electron confined in a region of size L. The electron can only move back and forth along a straight line of length L. Then the uncertainty in position must satisfy \(\Delta x\approx \frac{L}{2}\) and so the uncertainty in momentum must be:
\(\Delta p \approx \frac{h}{4\pi \Delta x}\approx \frac{h}{2\pi L}\)
The electron must then have a kinetic energy of:
\(E_k=\frac{p^2}{2m}\approx\frac{(\Delta p)^2}{2m} =\frac{h^2}{8\pi^2 mL^2}\)
We may apply this result to an electron in the hydrogen atom
The size of the region within which the electron is confined is about \(L\approx 10^{-10} m \). Then
\(L\approx 10^{-10}\)
or
\(E_k\simeq 4eV\)
which is in fact just about right for the electron’s kinetic energy. This shows that the uncertainty principle is an excellent tool for making approximate estimates for various quantities.
If we consider electron in Nucleus then \(L\approx 10^{-15} m \).
\(E_k\simeq 4 \times 10^{10} eV\) which is very to get confined in nucleus and hence electron cannot reside in nucleus.
Uncertainty in energy and time
The uncertainty principle also applies to measurements of energy and time. If the energy of a state is measured with an uncertainty \(\Delta E\) , then the lifetime of the state is of order \(\Delta t\) such that:
\(\Delta E\Delta t\geq \frac{h}{4\pi}\)
This is also applies to decaying particles, where \(\Delta E\) is the uncertainty in the measured value of the energy released and \(\Delta t\) is the lifetime of the particle.
ATOMS
THOMSON’S ATOMIC MODEL
- large scattering angle of α-particle
- origin of spectral lines observed in the spectrum of hydrogen atom
ALPHA-PARTICLE SCATTERING AND RUTHERFORD’S NUCLEAR MODEL OF ATOM
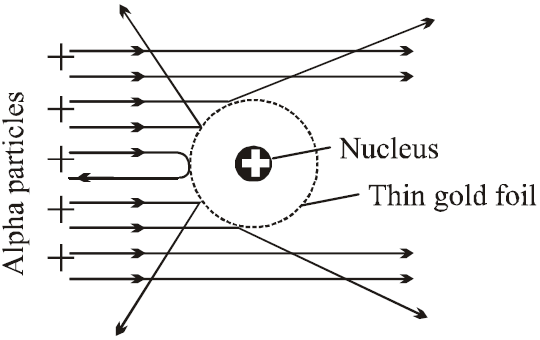
- Most of the α-particles went straight through the gold foil and produced flashes on the screen as if there were nothing inside gold foil. This suggests that the most part of the atom is empty.
- Few particles collided with the atoms of the foil which have scattered or deflected through considerable large angles. Very few particles even turned back towards source itself.
- The entire positive charge and almost whole mass of the atom is concentrated in small centre called a nucleus.
- The electrons revolving round the nucleus could not deflected the path of α-particles. This suggests that electrons are very light.
α-particles scattered at angle θ by a target,
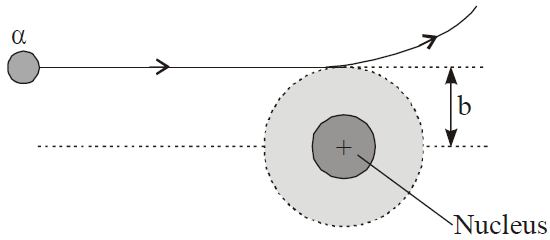
BOHR’S ATOMIC (HYDROGEN ATOM) MODEL
- The electron moves in circular orbits around the nucleus under the influence of coulombic force of attraction between the electron and the positively charged nucleus (as shown in figure below).
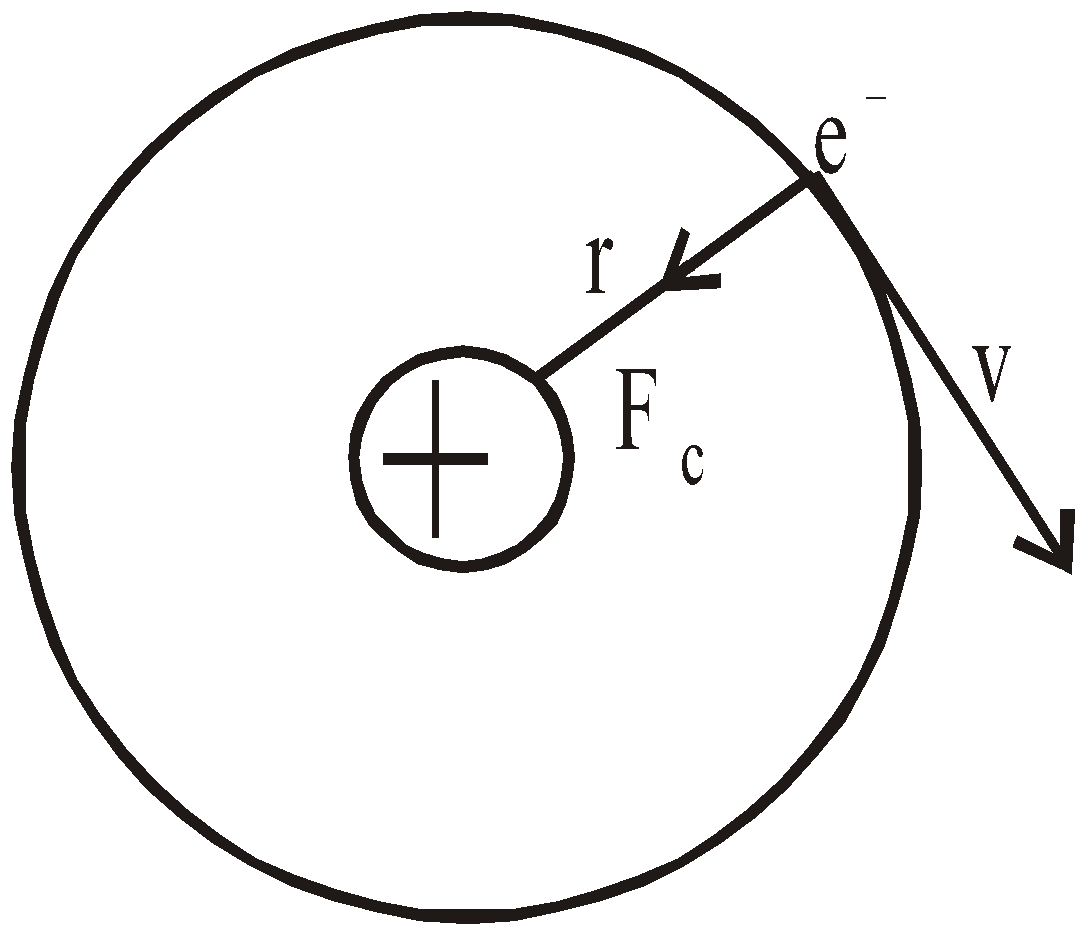
- The electron rotates about the nucleus in certain stationary circular orbits, for which the angular momentum of electron about the nucleus is an integral multiple of
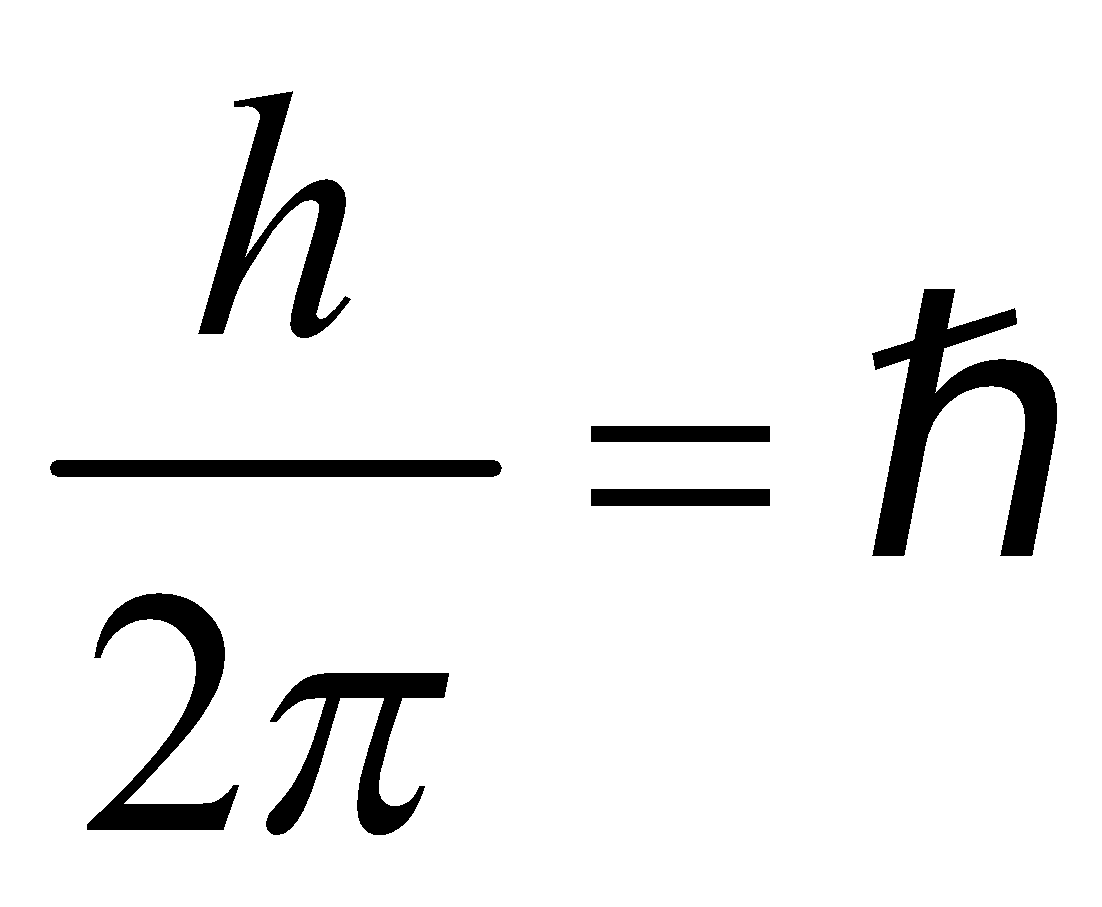 , where h is plank’s constant
, where h is plank’s constant
- When the electron is in one of its stationary orbits, it does not radiate energy, hence the atom is stable. These stationary orbits are called allowed orbits.
- The atom radiates energy when the electron “jumps” from one allowed stationery state to another. The frequency of radiation follows the condition
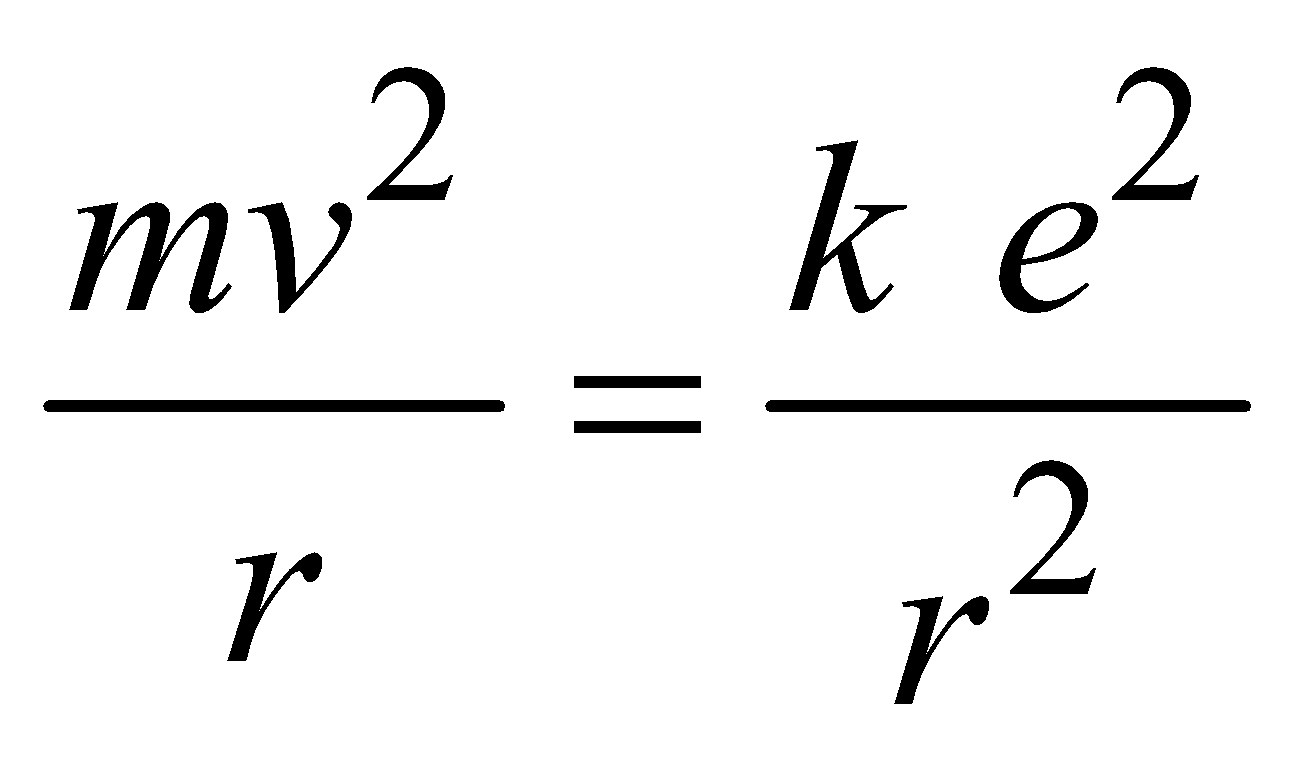 …(3)
…(3)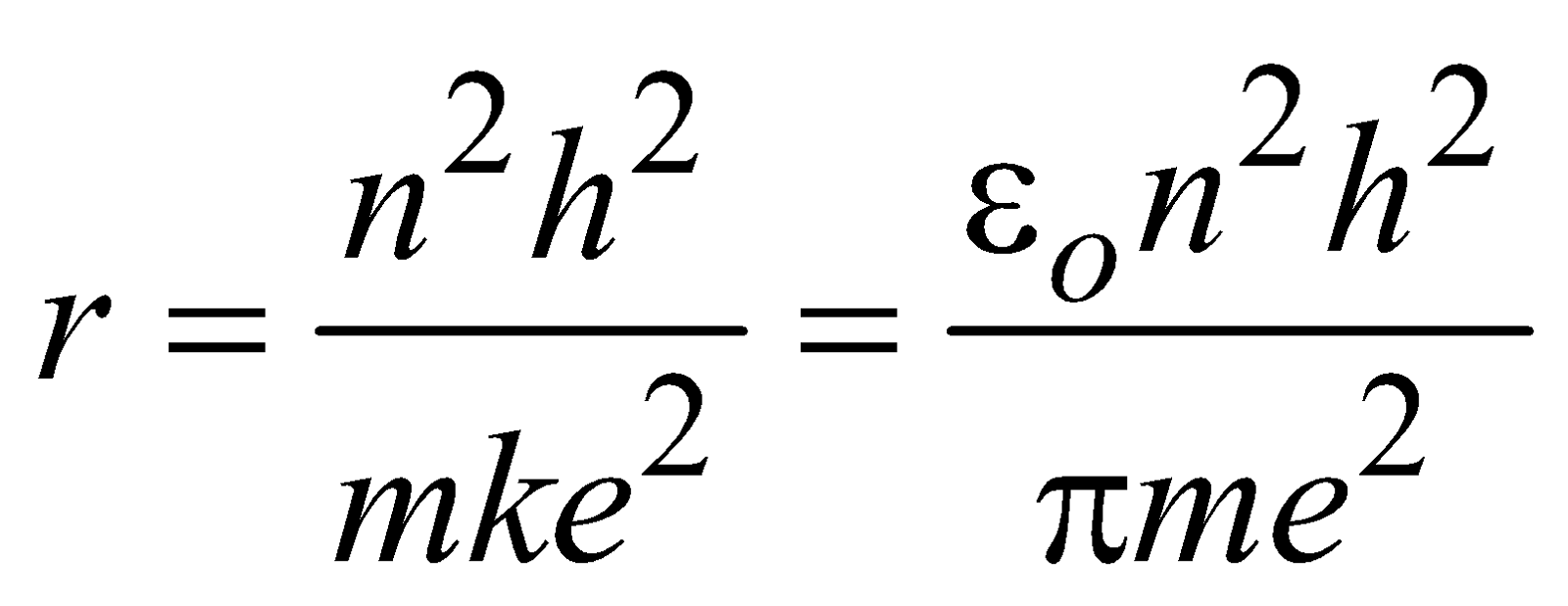 (where n = 1, 2, 3 …..) …(4)
(where n = 1, 2, 3 …..) …(4) 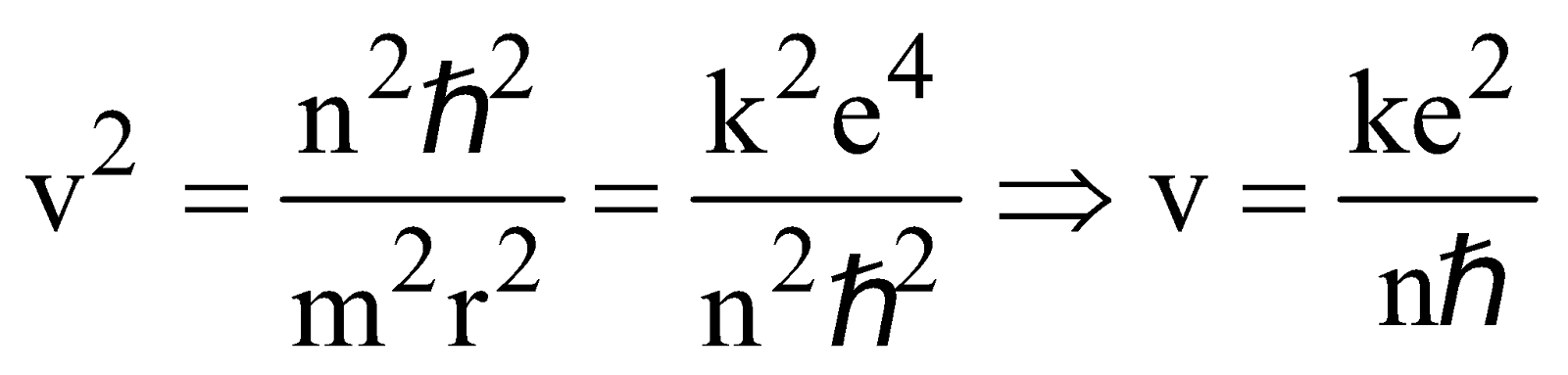
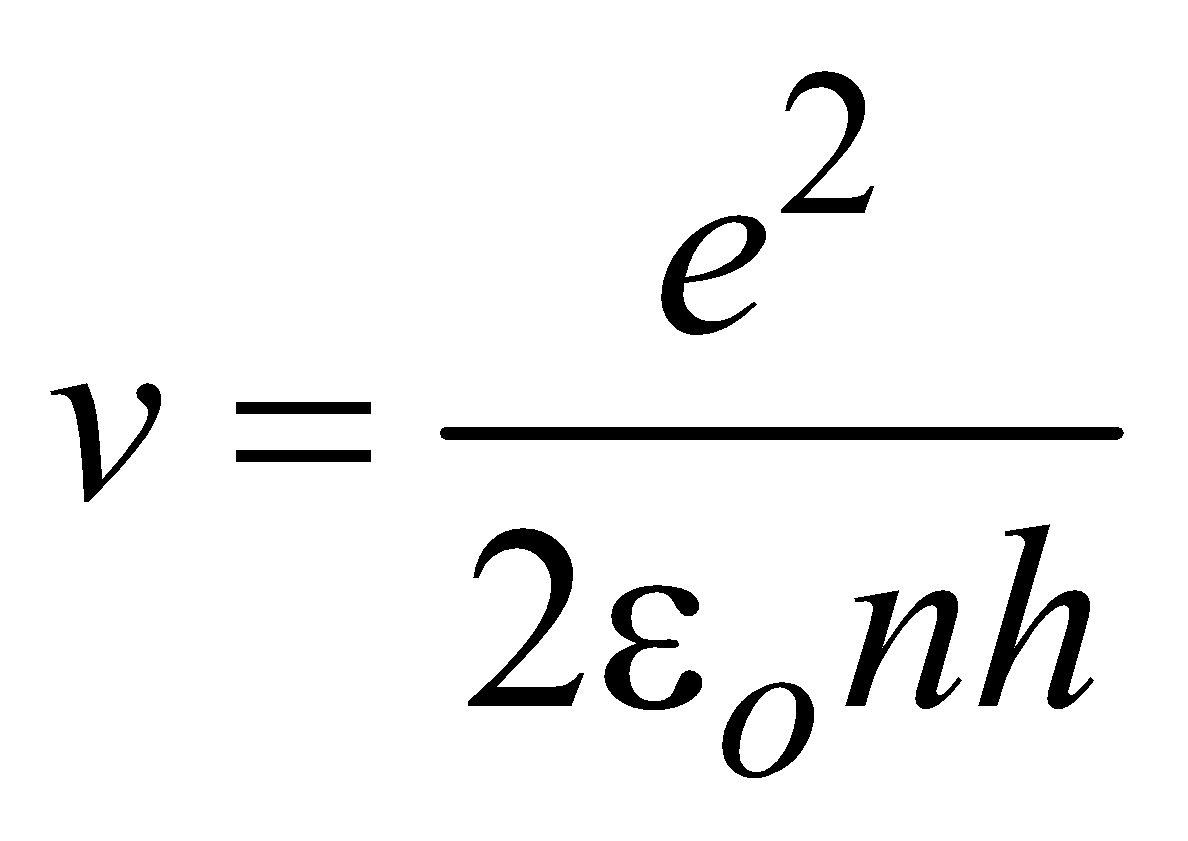
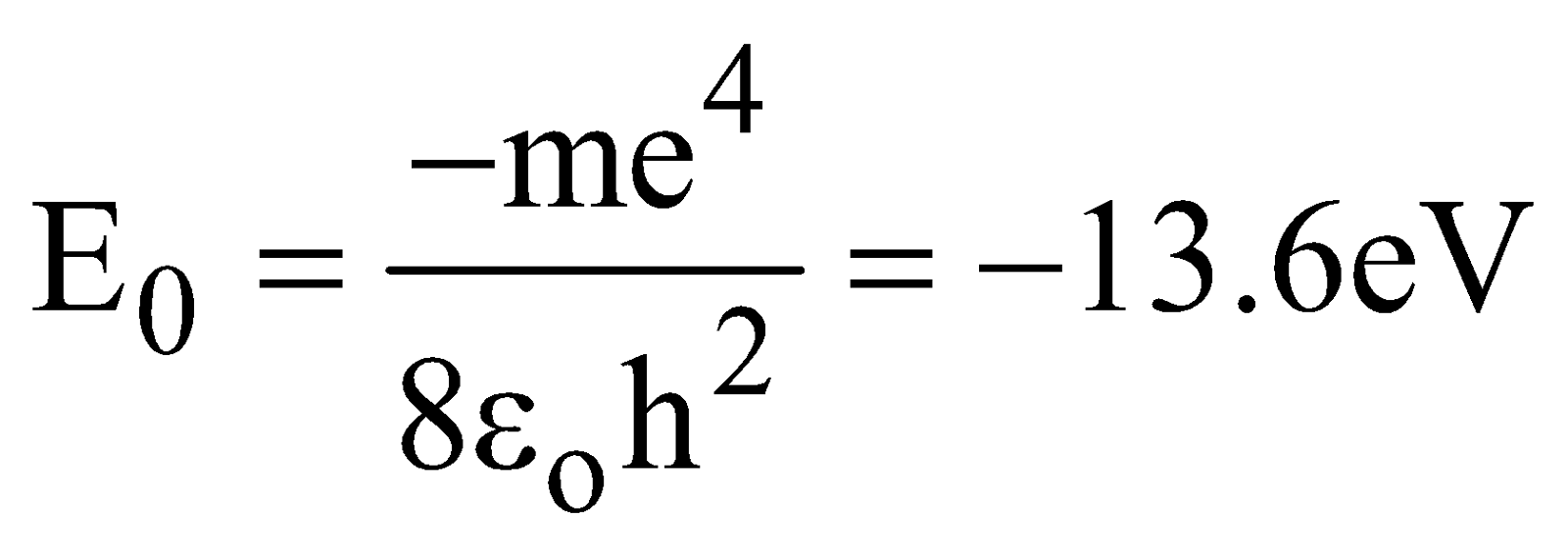
LIMITATIONS OF BOHR’S MODEL
- It could not explain the spectra of atoms containing more than one electron.
- There was no theoretical basis for selecting mvr to be an integral multiple of
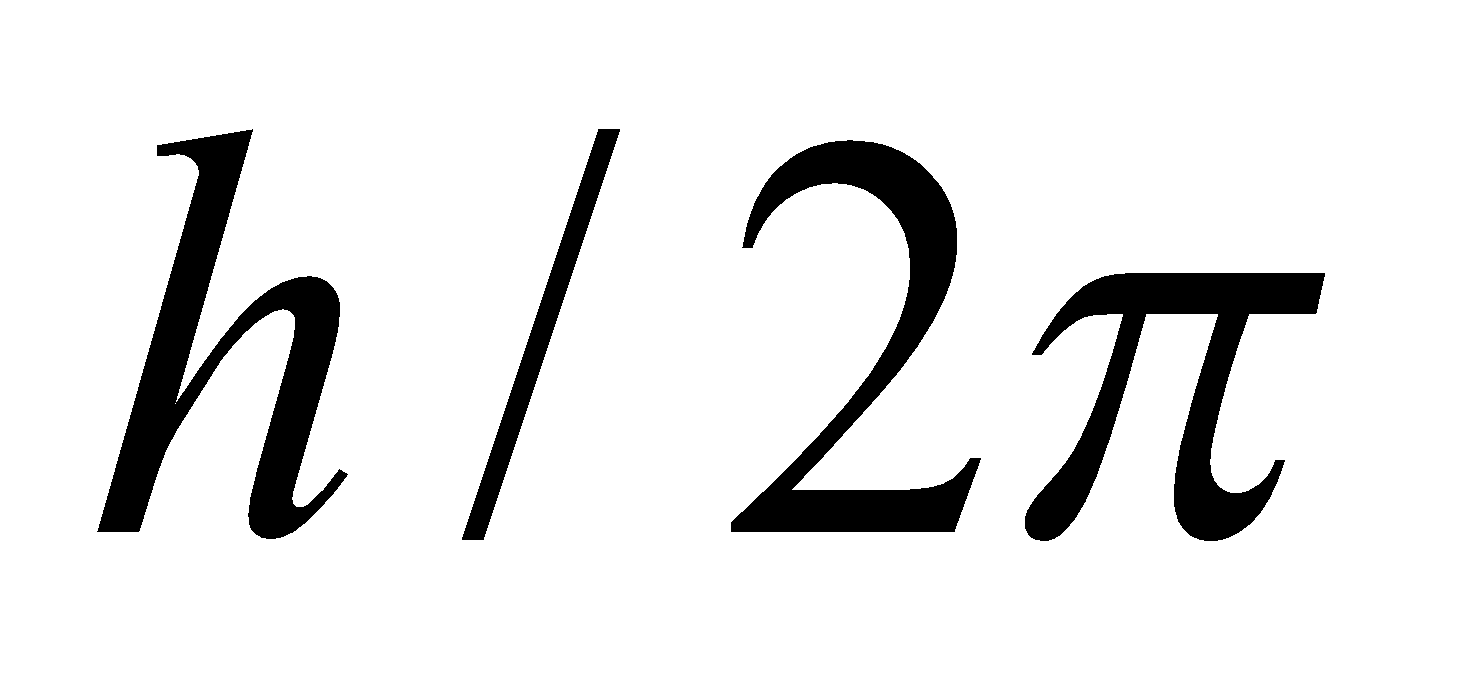 .
. - It involved the orbit concept which could not be checked experimentally.
- It could not explain Zeeman & Stark effect and fine lines of spectra.
- It was against de-Broglie concept and uncertainty principle.
- Total energy of electron = – Kinetic energy
- The reference level for potential energy has been taken as infinity
- The energy gap between two successive levels decreases as the value of n increases
- The radius difference between the successive orbit (or shells) increases as the value of n increases
- The velocity of electrons around the nucleus goes on decreasing as n increases
- The time period of the electron in an orbit
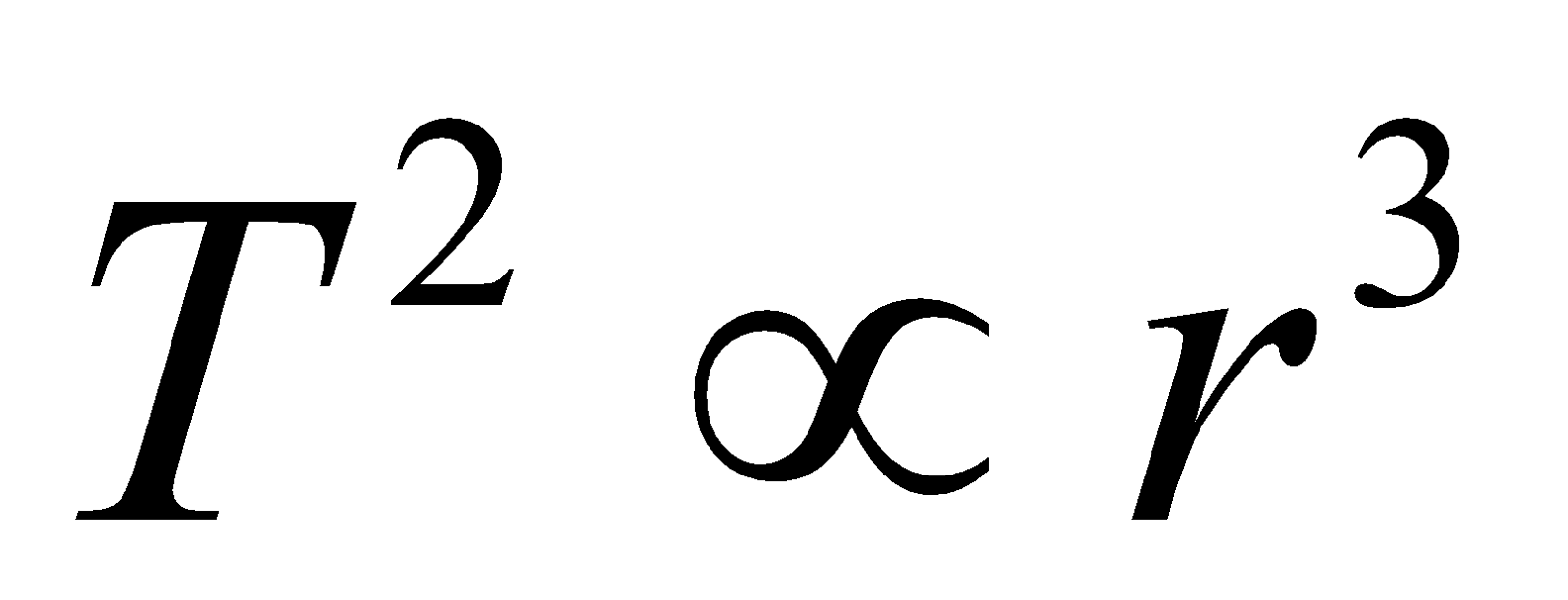
- Maximum number of spectral lines that can be emitted when an electron jumps from nth orbit is
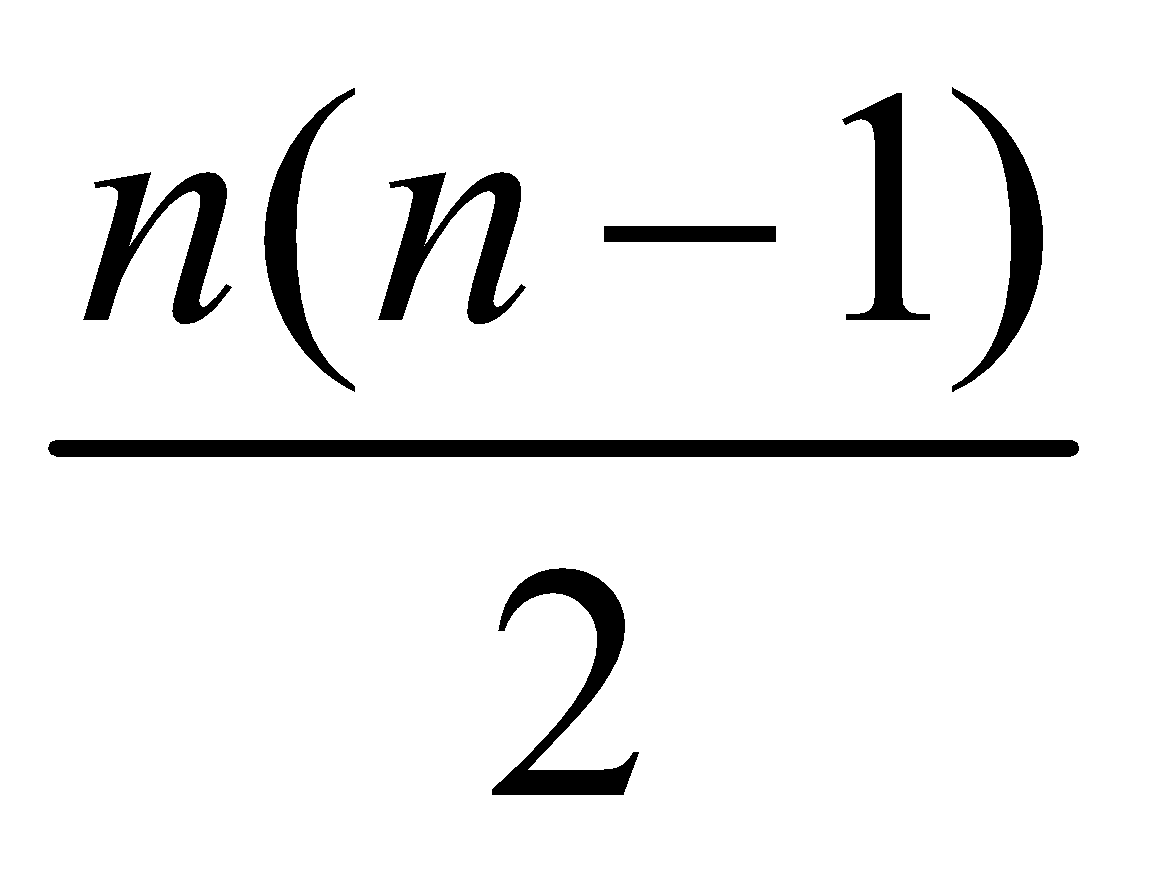
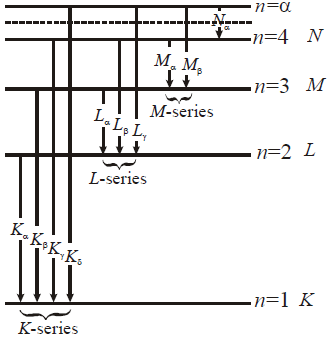
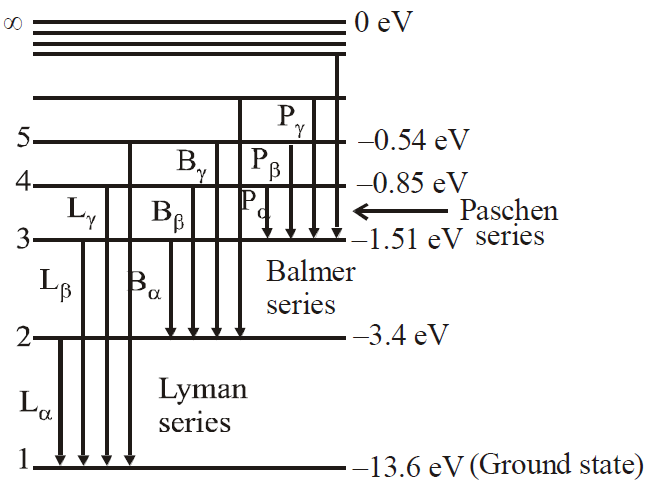
ENERGY LEVELS AND THE LINES SPECTRA OF HYDROGEN ATOM
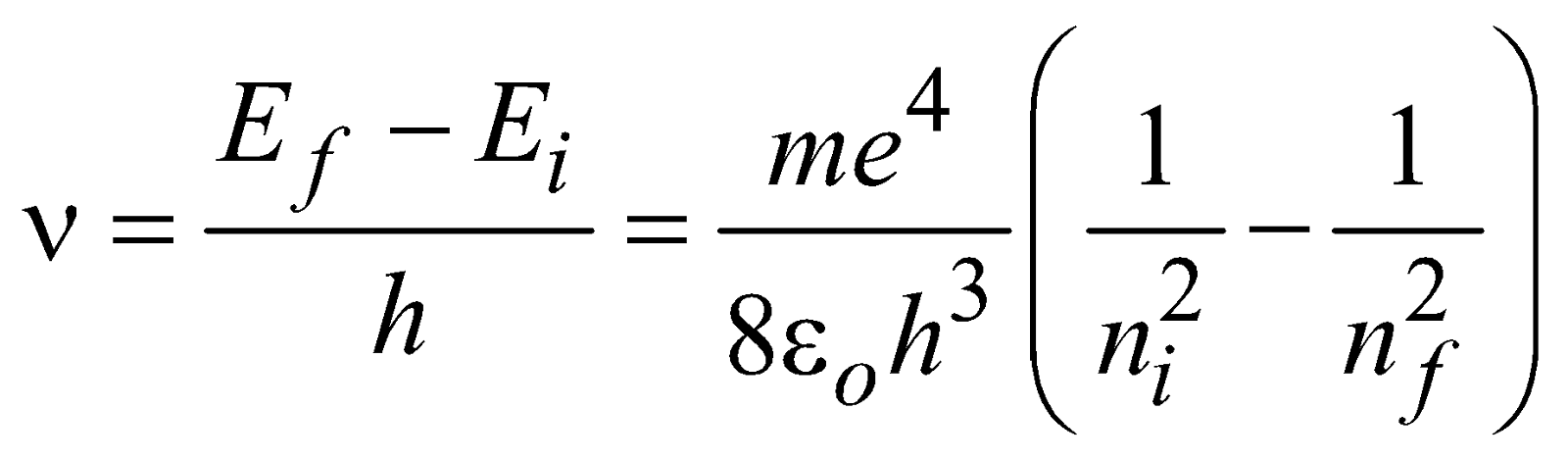 …(1)
…(1)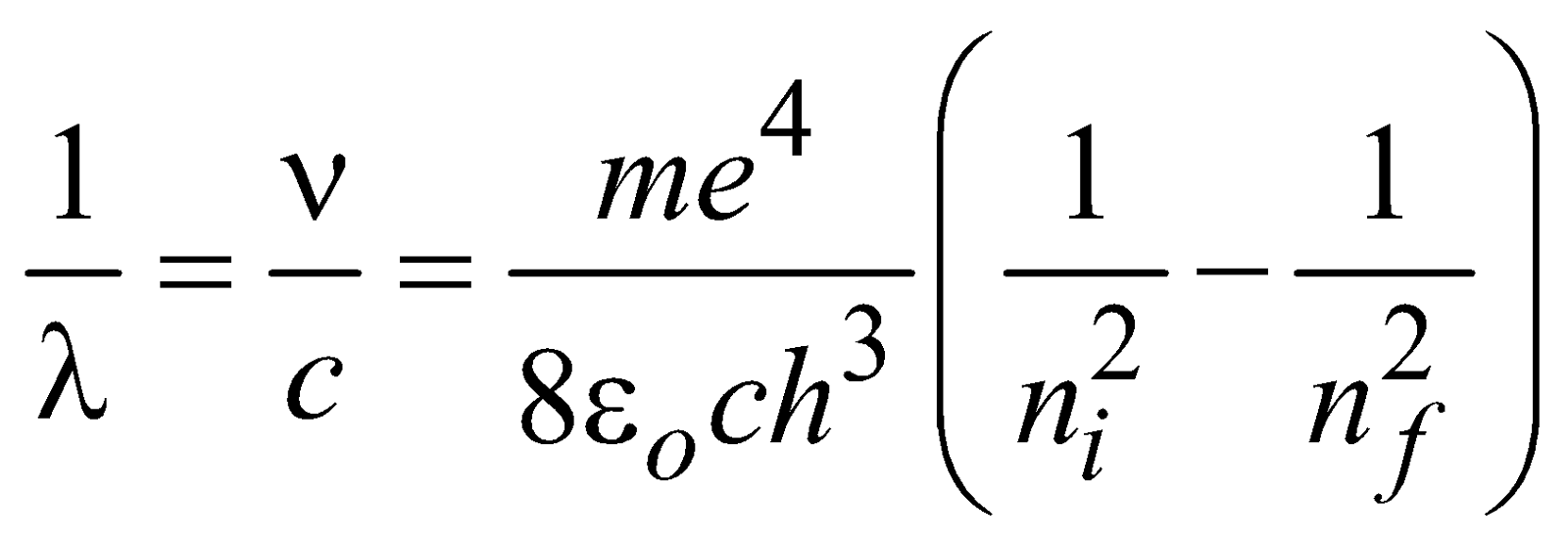
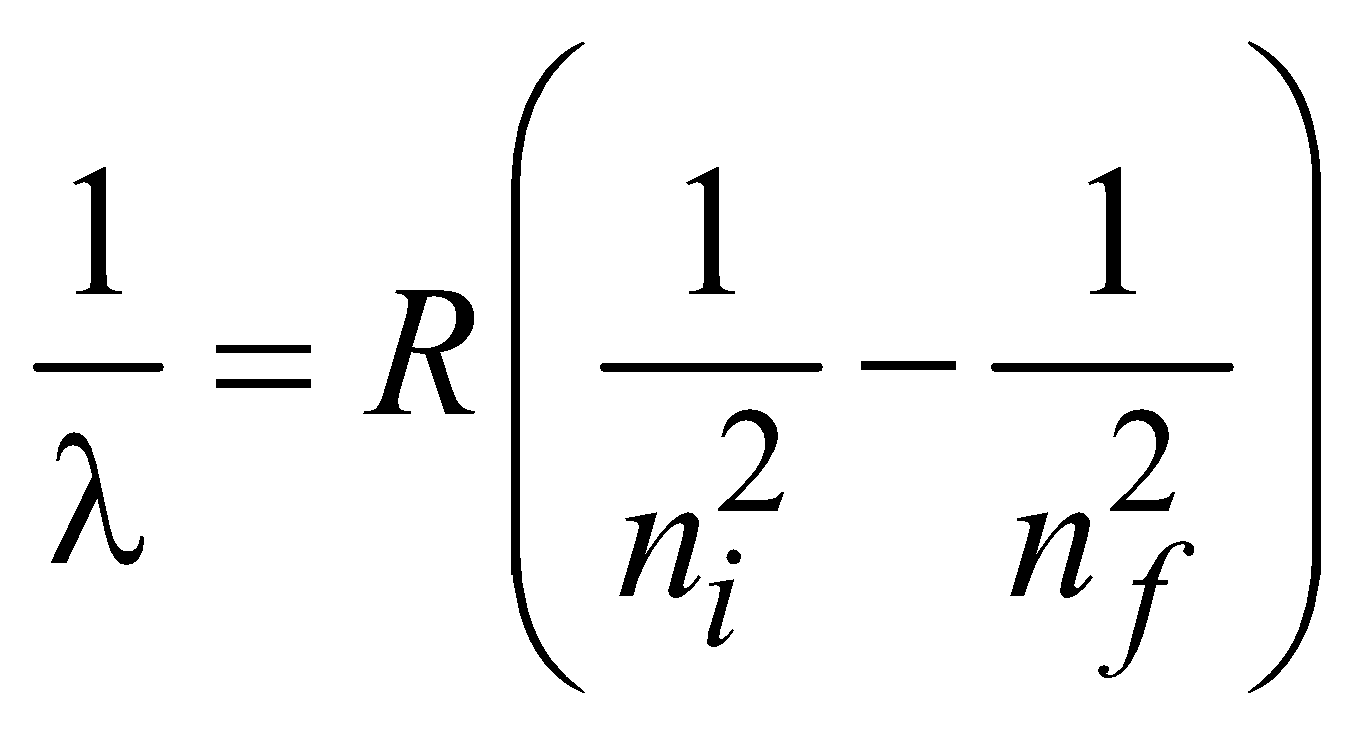 for hydrogen atom …(2)
for hydrogen atom …(2)- Lyman series ni = 1 & nf = 2, 3, 4……………
- Balmer series ni = 2, & nf = 3, 4, 5……………
- Paschen series ni = 3 & nf = 4, 5, 6…………..
- Brackett series ni = 4 & nf = 5, 6, 7……………
- P fund series ni = 5 & nf = 6, 7, 8……………
WAVELENGTH LIMITS IN VARIOUS SPECTRAL SERIES OF HYDROGEN ATOM
- For Lyman series (lies in ultraviolet region)
- For Balmer series (lies in visible region)
- For Paschen series (lies in infrared region)
- For Brackett series (lies in infrared region)
- For p-fund series (lies in infrared region)
Here
- The first line of Lyman series is when electron jumps from 2 → 1, It is also called α–line
- Energy of electrons in different orbits in an atom varies inversely with the square of the number of orbits. So, energy of electrons increases (decreases in negative) as the orbit becomes higher.
- If energy of a particular orbit is E for H-atom then its value for a H-like atom with atomic number Z is given by E’ = E × Z2.
- If the radius of a particular orbit of H-atom is R then its value for a H-like atom is given by
- If velocity of an electron in a particular orbit of H-atom be v then its value for H-like atom is given by
- If kinetic energy and potential energy of an electron in a particular orbit of H-atom be T and V respectively then their corresponding values for H-like atom are given by
T’ = T × Z2 and V’ = V× Z2.