7.1 Discrete energy and radioactivity
Essential Idea:
In the microscopic world energy is discrete.
Understandings:
- Discrete energy and discrete energy levels
- Transitions between energy levels
- Radioactive decay
- Fundamental forces and their properties
- Alpha particles, beta particles and gamma rays
- Half-life
- Absorption characteristics of decay particles
- Isotopes
- Background radiation
Applications and Skills:
- Describing the emission and absorption spectrum of common gases
- Solving problems involving atomic spectra, including calculating the wavelength of photons emitted during atomic transitions
- Completing decay equations for alpha and beta decay
- Determining the half-life of a nuclide from a decay curve
- Investigating half-life experimentally (or by simulation)
Data booklet reference:
- E = hf
- \(\lambda =\frac{hc}{E}\)
ATOMS
THOMSON’S ATOMIC MODEL
This model suggests an atom to be a tiny sphere of radius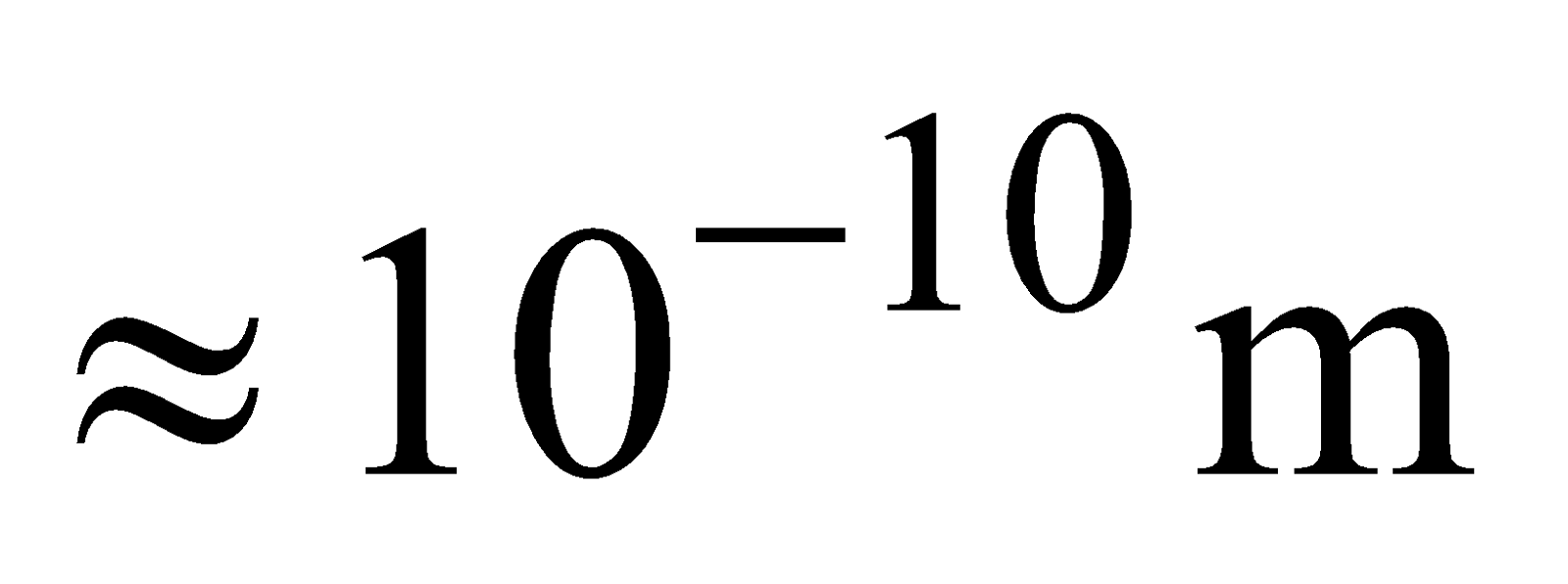 , containing the positive charge. The atom is electrically neutral. It contains an equal negative charge in the form of electrons, which are embedded randomly in this sphere, like seeds in a watermelon.
, containing the positive charge. The atom is electrically neutral. It contains an equal negative charge in the form of electrons, which are embedded randomly in this sphere, like seeds in a watermelon.
This model failed to explain
- large scattering angle of α-particle
- origin of spectral lines observed in the spectrum of hydrogen atom
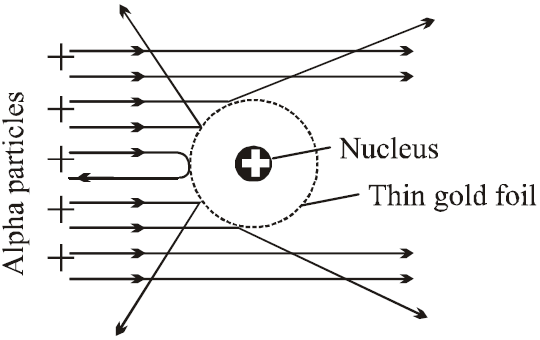
ALPHA-PARTICLE SCATTERING AND RUTHERFORD’S NUCLEAR MODEL OF ATOM
In Rutherford α- particle scattering experiment a very fine beam of α-particle passes through a small hole in the lead screen. This well collimated beam is then allowed to fall on a thin gold foil. While passing through the gold foil, α-particles are scattered through different angles. A zinc sulphide screen is placed out the other side of the gold foil, this screen is movable, so as to receive the α-particles, scattered from the gold foil at angles varying from 0 to 180°. When a α-particle strikes the screen, it produces a flash of light.
FINDINGS
- Most of the α-particles went straight through the gold foil and produced flashes on the screen as if there were nothing inside gold foil. This suggests that the most part of the atom is empty.
- Few particles collided with the atoms of the foil which have scattered or deflected through considerable large angles. Very few particles even turned back towards source itself.
CONCLUSIONS
- The entire positive charge and almost whole mass of the atom is concentrated in small centre called a nucleus.
- The electrons revolving round the nucleus could not deflected the path of α-particles. This suggests that electrons are very light.
In 1911 Rutherford, proposed a new type of model of the atom. According to this model, the positive charge of the atom, instead of being uniformly distributed throughout a sphere of atomic dimension is concentrated in a very small volume at its centre. This central core, called nucleus, is surrounded by clouds of electrons makes the entire atom electrically neutral.
According to Rutherford scattering formula, the number of
α-particles scattered at angle θ by a target,
α-particles scattered at angle θ by a target,
N ∝ cosec4 (θ/2)
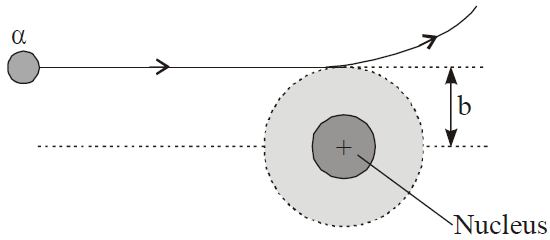
Impact parameter
Distance of closest approach
RESULT OF RUTHERFORD SCATTERING EXPERIMENT
Nucleus is central, massive, positively charged core, its size of the order of 10–15 m, number of electrons surrounding nucleus is such that atom is electrically neutral.
Unit for nuclear dimension measurement : 1 fermi = 10–15m.
BOHR’S ATOMIC (HYDROGEN ATOM) MODEL
In 1913 Bohr gave his atomic theory primarily to explain, the spectra of hydrogen and hydrogen-like atoms. His theory, contained a combination of views from Plank’s quantum theory, Einstein’s photon concept and Rutherford model of atom. The Bohr theory can explain, the atomic spectra of hydrogen atom and hydrogen-like ions such as He+, Li2+, Be3+…(one electron ions). But his theory failed to explain, the spectra of more complex atom and ions.
BASIC POSTULATES OF BOHR’S MODEL
- The electron moves in circular orbits around the nucleus under the influence of coulombic force of attraction between the electron and the positively charged nucleus (as shown in figure below).
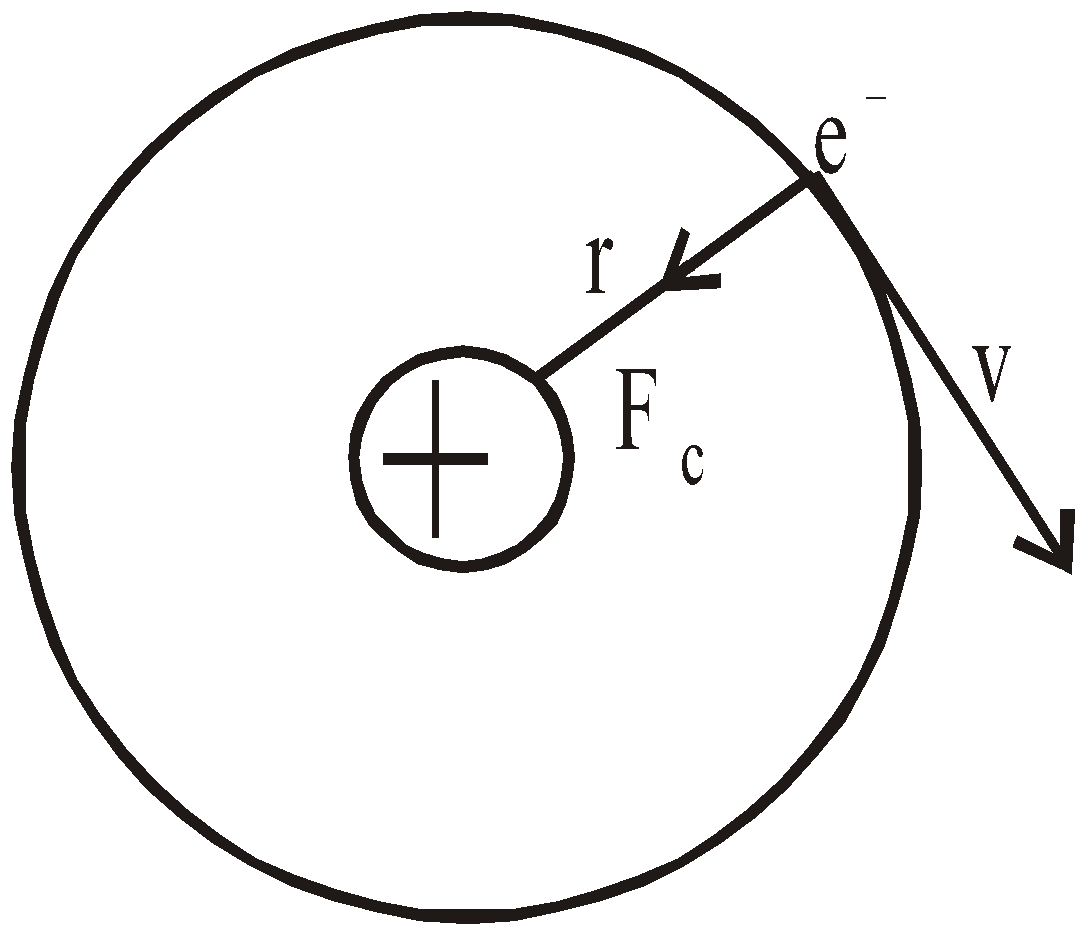
Bohr’s model of hydrogen atom
- The electron rotates about the nucleus in certain stationary circular orbits, for which the angular momentum of electron about the nucleus is an integral multiple of
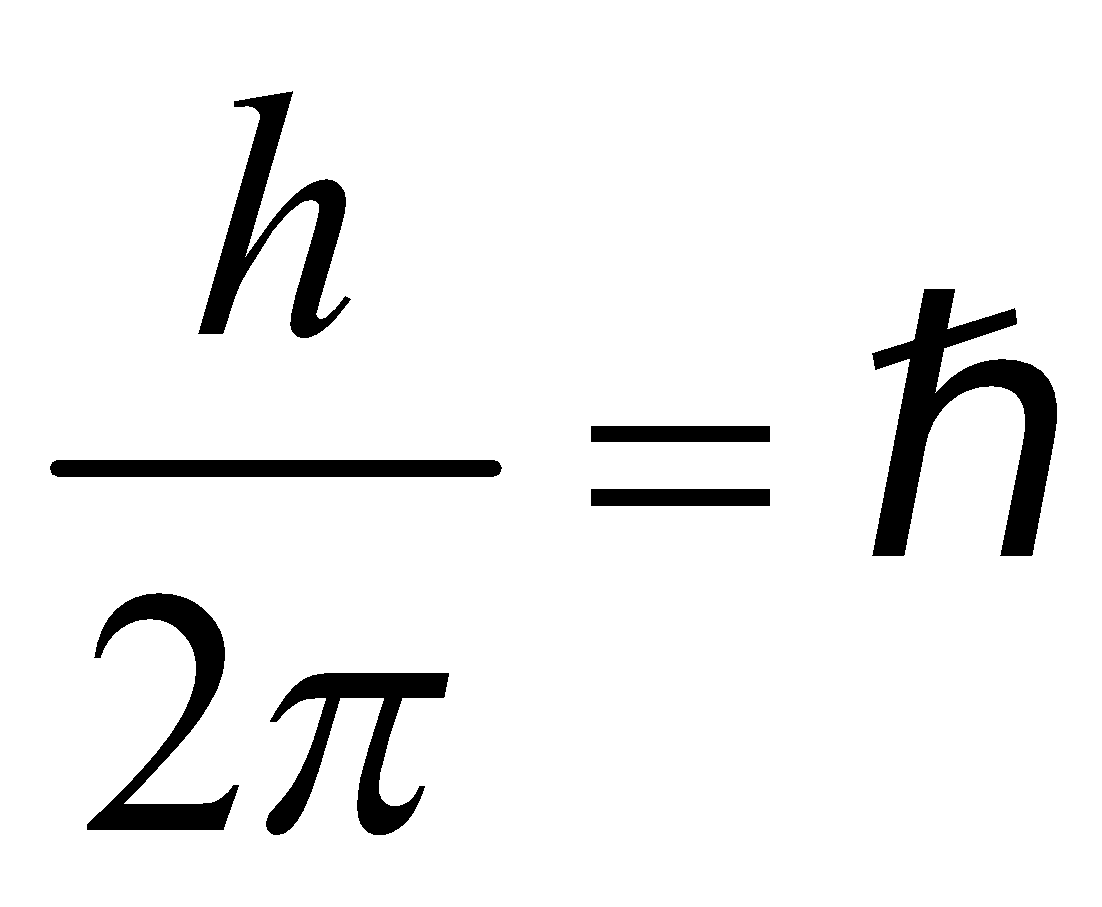 , where h is plank’s constant
, where h is plank’s constant
i.e., Angular Momentum, 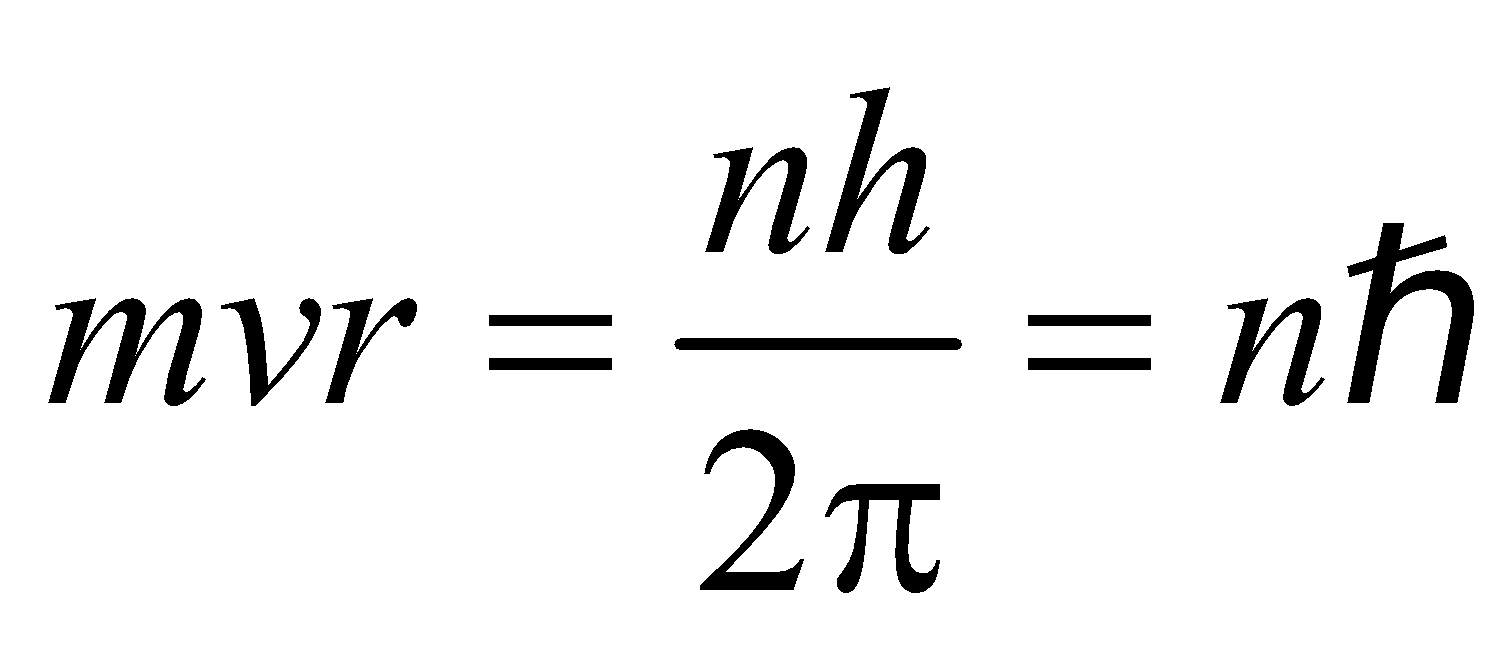 …(1)
…(1)
(where n = 1, 2, 3……… principal quantum number)
- When the electron is in one of its stationary orbits, it does not radiate energy, hence the atom is stable. These stationary orbits are called allowed orbits.
- The atom radiates energy when the electron “jumps” from one allowed stationery state to another. The frequency of radiation follows the condition
hν = Ei – Ef …(2)
Where Ei and Ef are total energies of initial and final stationary states. This difference in energy (Ei -Ef) between two allowed stationary states is radiated/absorbed in the form of a packet of electromagnetic energy (hν – one photon of frequency ν) called a photon.
Now we calculate the allowed energies of hydrogen atom,
For moving an electron in a circular orbit the required centripetal force is provided by the coulomb force of attraction which acts between nucleus [Ze+, here Z = 1 (atomic number) for hydrogen atom] & electron (e–),
i.e., 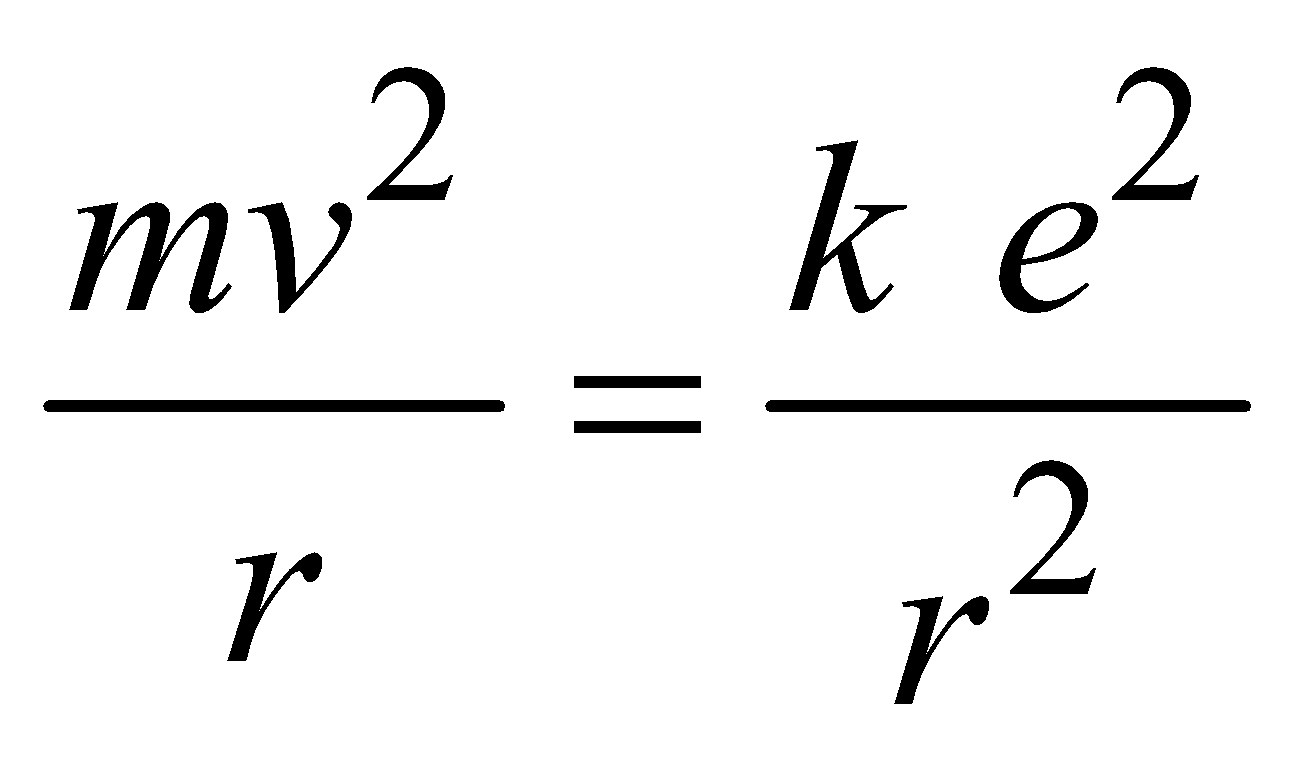 …(3)
…(3)
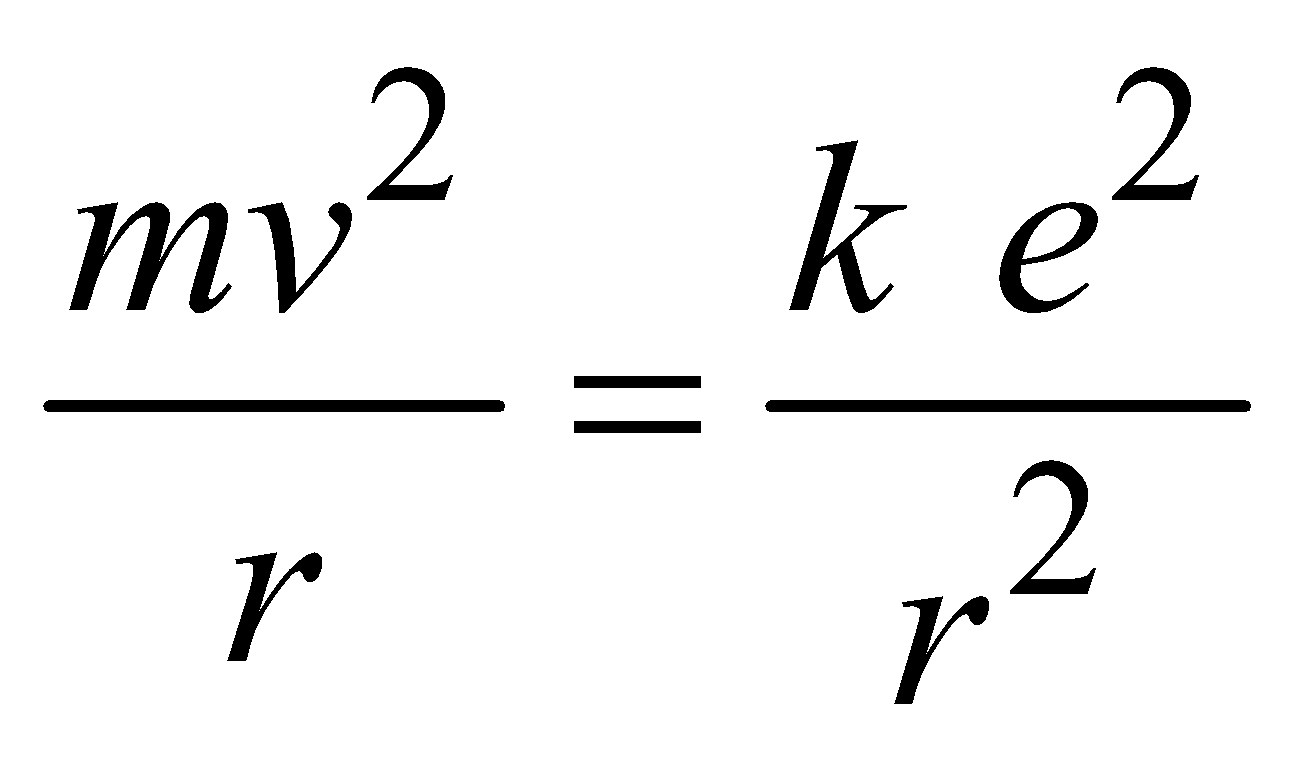 …(3)
…(3)where 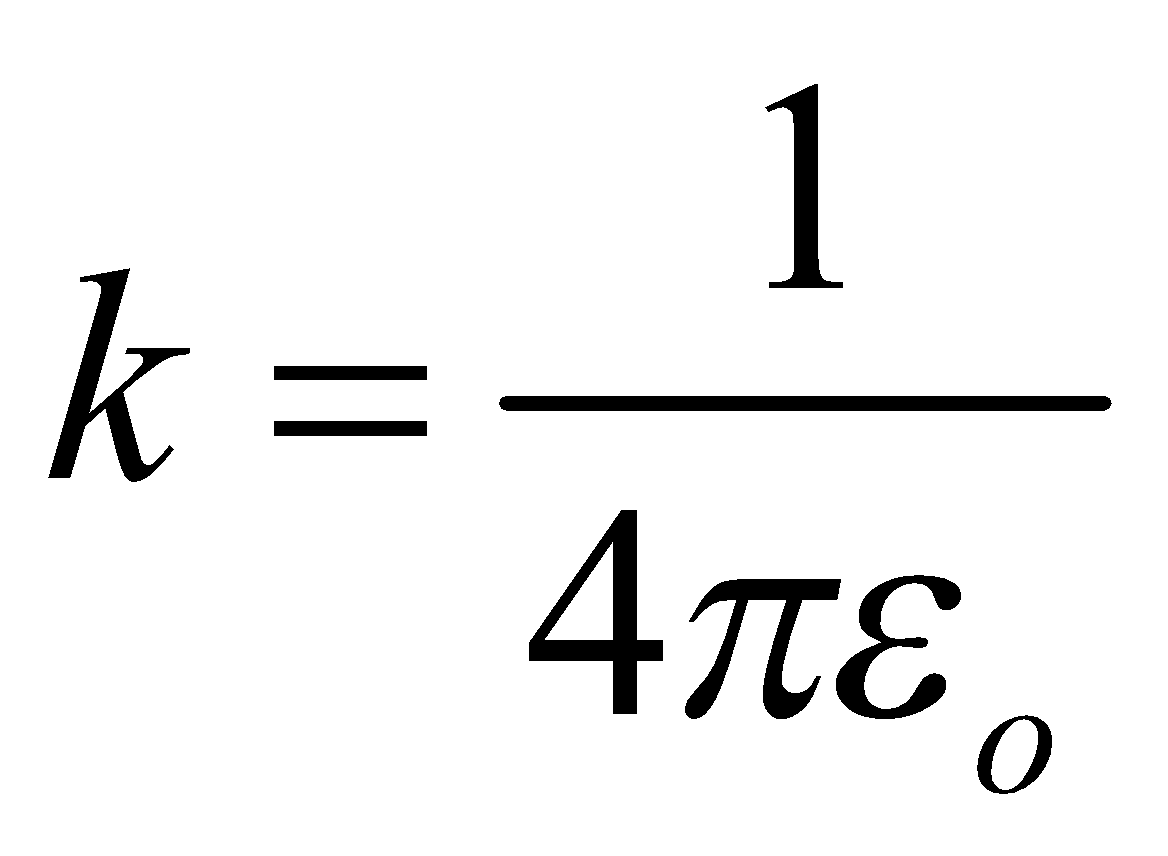 is electrostatic constant & εo is permittivity of free space.
is electrostatic constant & εo is permittivity of free space.
Eliminating v from eqn. (1) and (3) we obtain radius of nth orbit
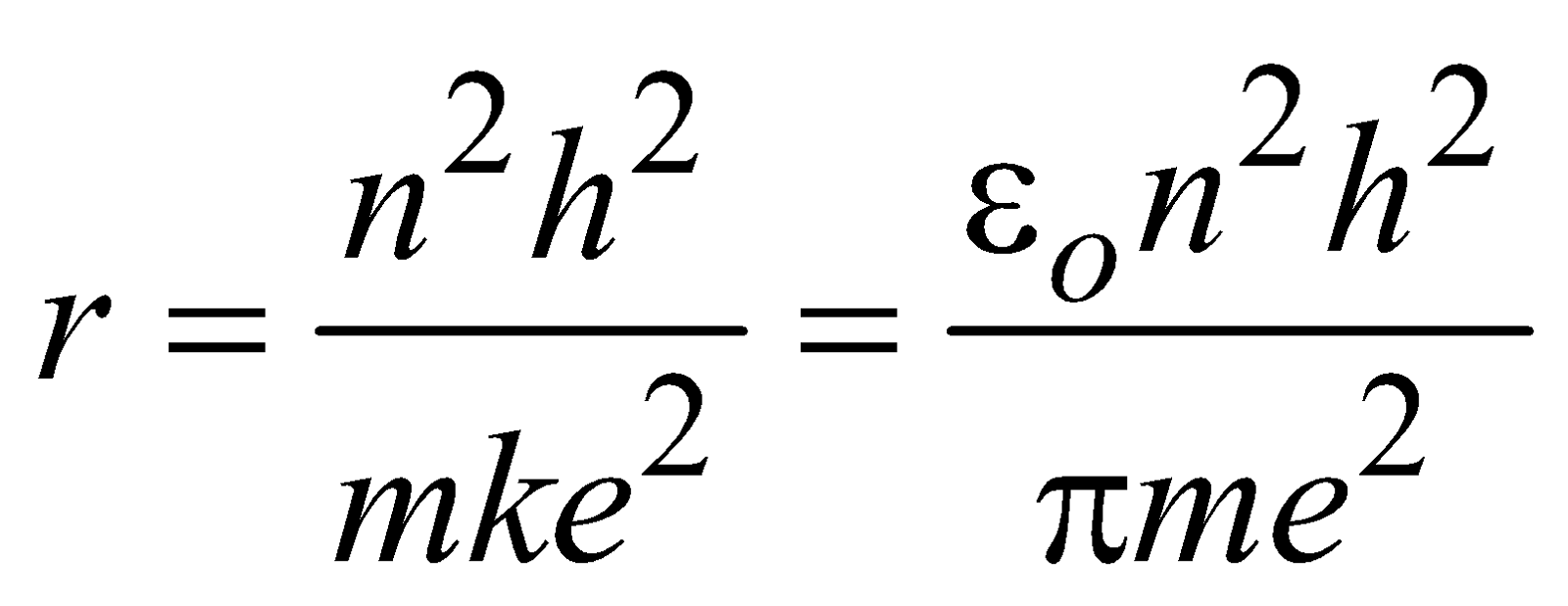 (where n = 1, 2, 3 …..) …(4)
(where n = 1, 2, 3 …..) …(4) Equation (4) gives the radii of various orbits (have discrete values).
The smallest radius (also called Bohr radius) corresponds to n = 1 is
⇒ r = 0.529 n2 Å for hydrogen atom and
r = 0.529 × 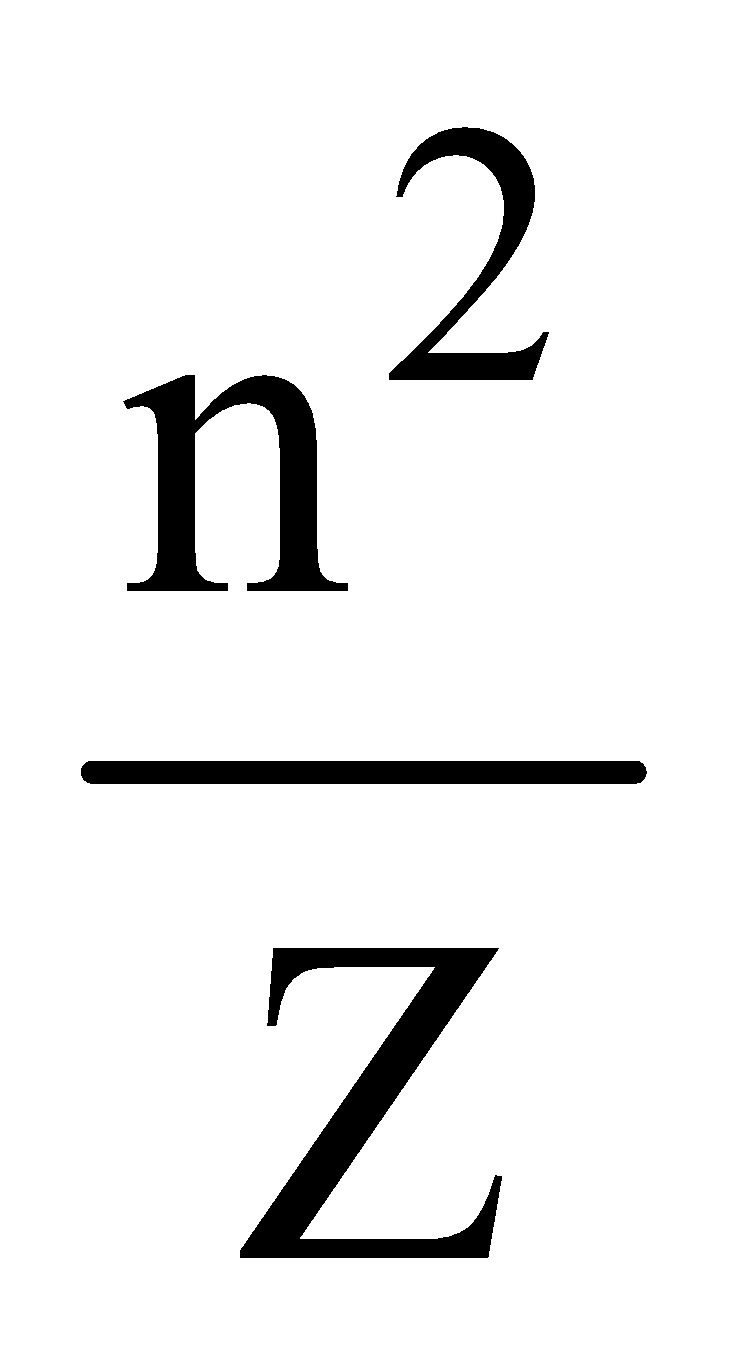 for hydrogen like ions.
for hydrogen like ions.
From equation (4) & (1) we obtain,
Velocity of electron in nth state
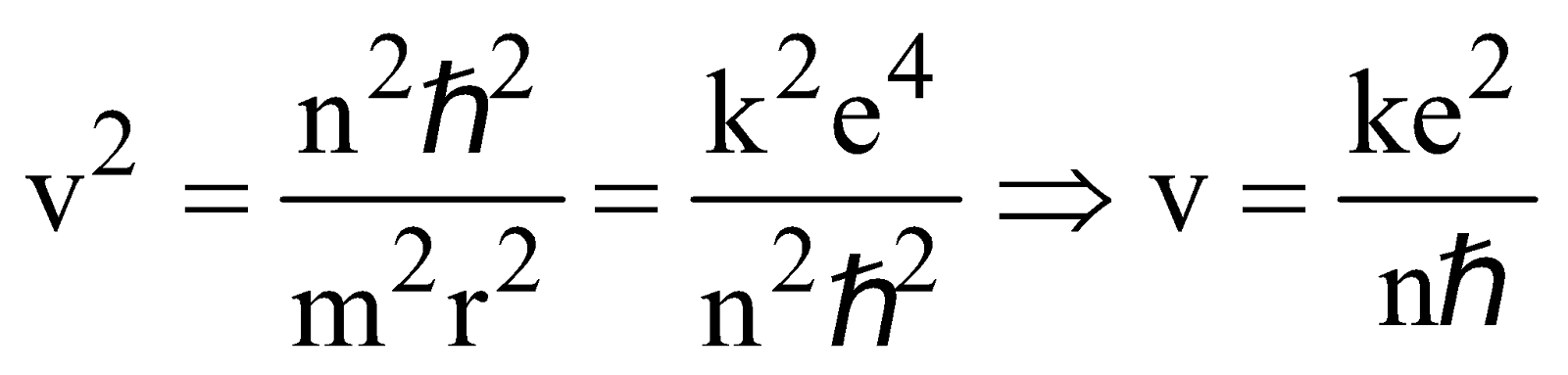
or 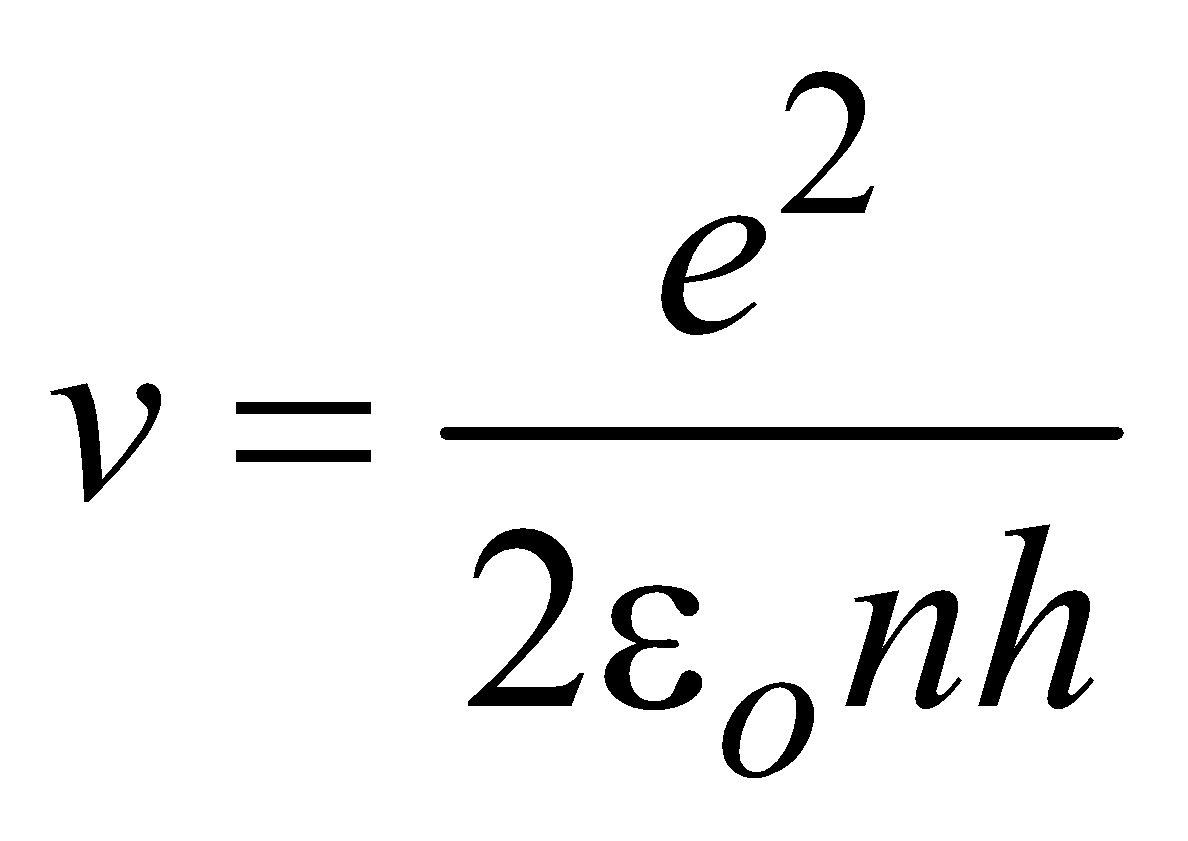
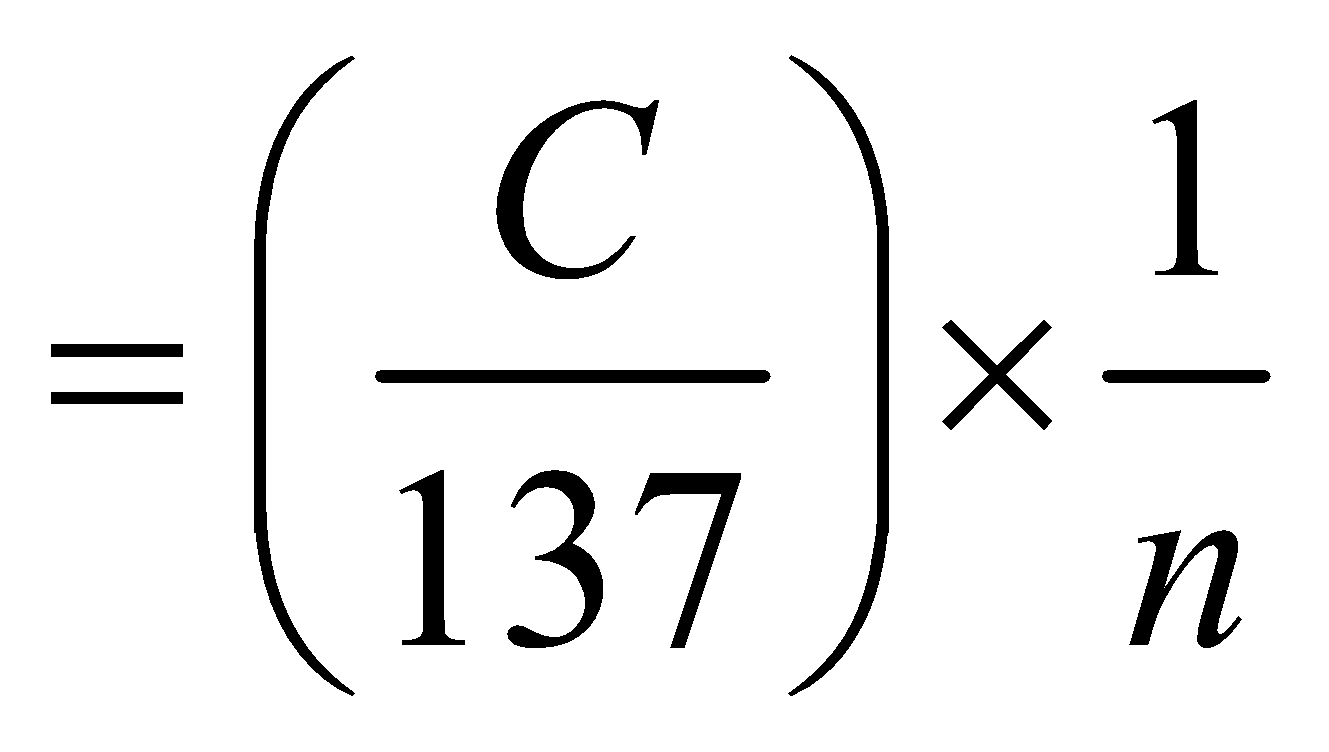 (for hydrogen atom ) …(6)
(for hydrogen atom ) …(6)
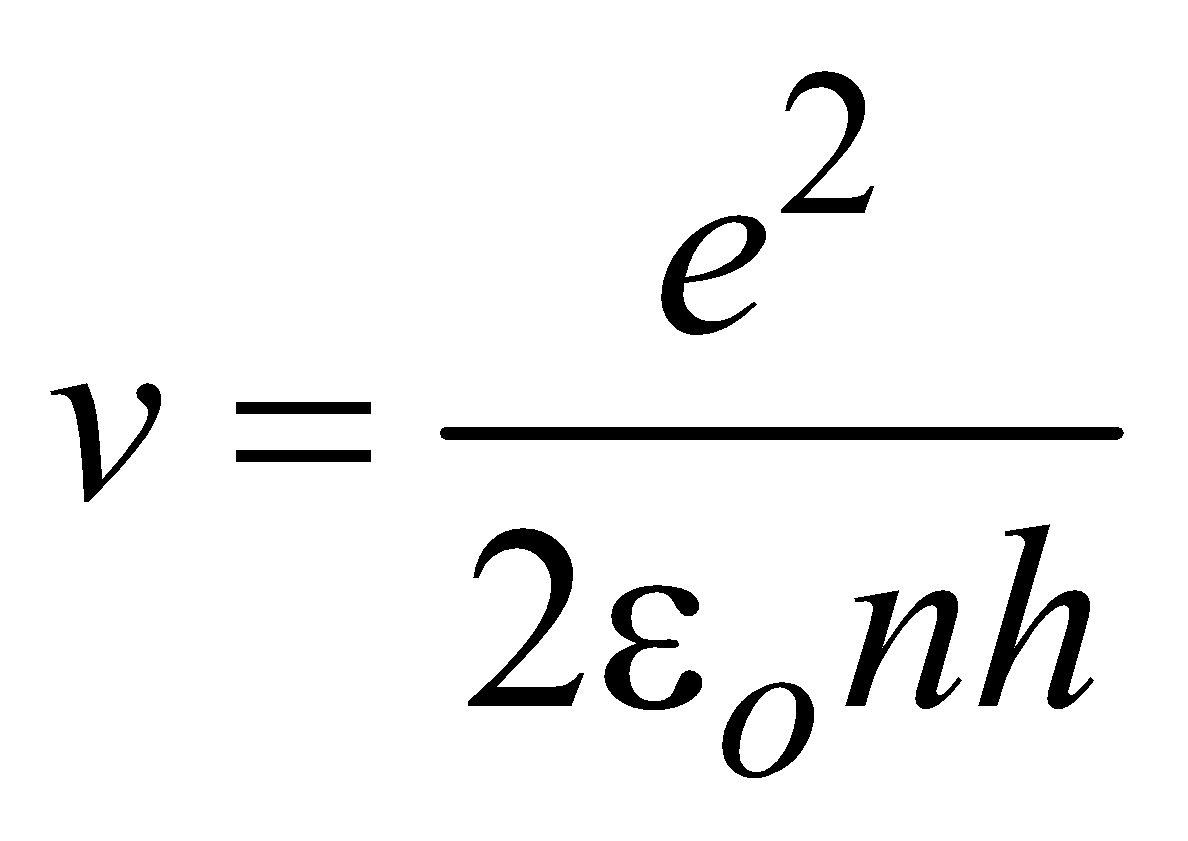
The total energy of electron is given by
E = K.E. + P.E. = Kinetic energy + Potential energy
(Allowed energy state)
After substituting numerical values in eqn.(7), we obtain
The lowest energy state, or ground state, corresponds to n = 1 is
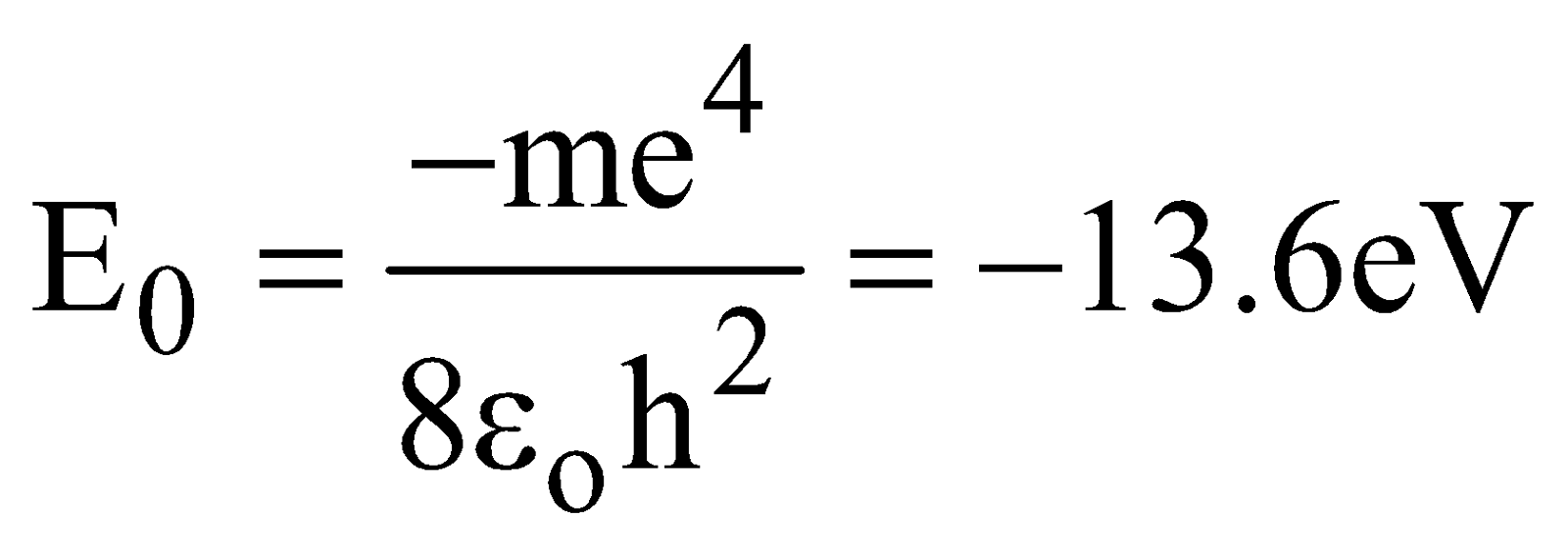
The next state corresponds to n = 2 i.e., first excited state has an energy, E = –3.4 eV
LIMITATIONS OF BOHR’S MODEL
- It could not explain the spectra of atoms containing more than one electron.
- There was no theoretical basis for selecting mvr to be an integral multiple of
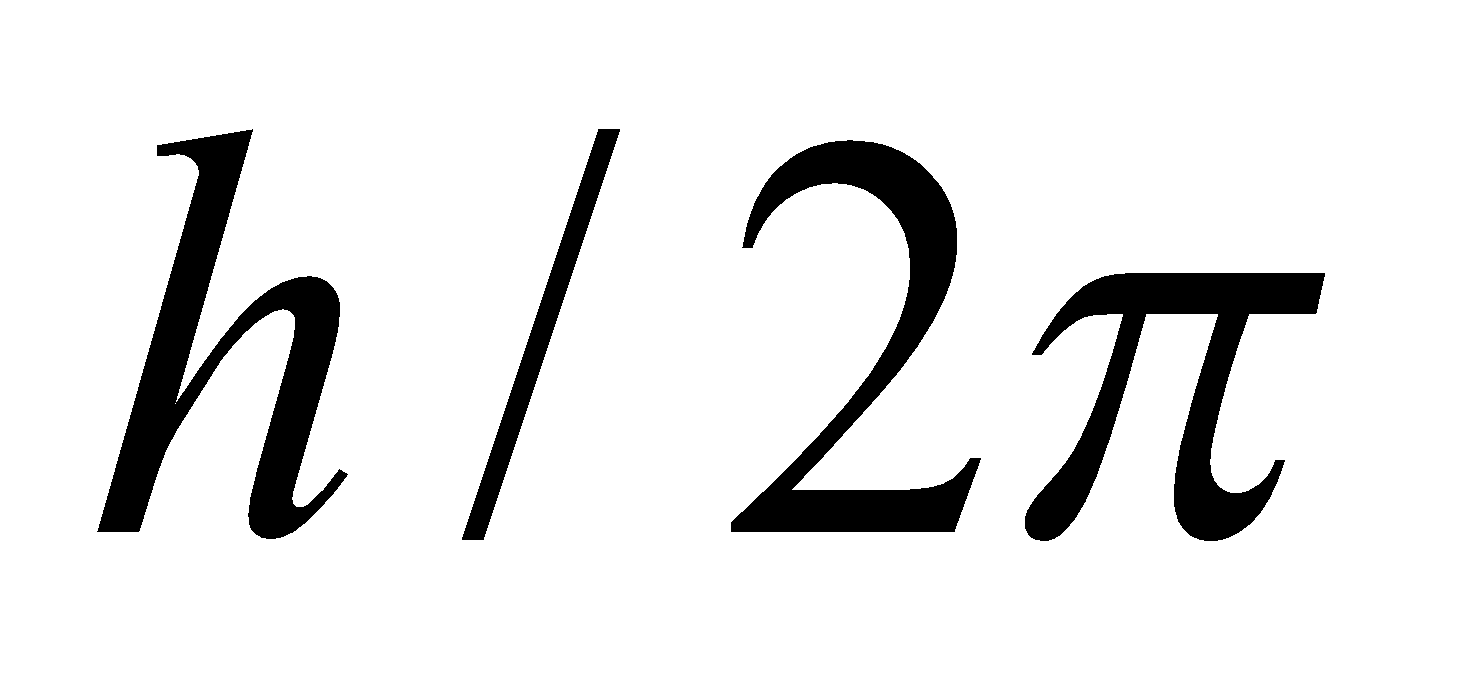 .
. - It involved the orbit concept which could not be checked experimentally.
- It could not explain Zeeman & Stark effect and fine lines of spectra.
- It was against de-Broglie concept and uncertainty principle.
KEEP IN MEMORY
- Total energy of electron = – Kinetic energy
- The reference level for potential energy has been taken as infinity
- The energy gap between two successive levels decreases as the value of n increases
- The radius difference between the successive orbit (or shells) increases as the value of n increases
- The velocity of electrons around the nucleus goes on decreasing as n increases
- The time period of the electron in an orbit
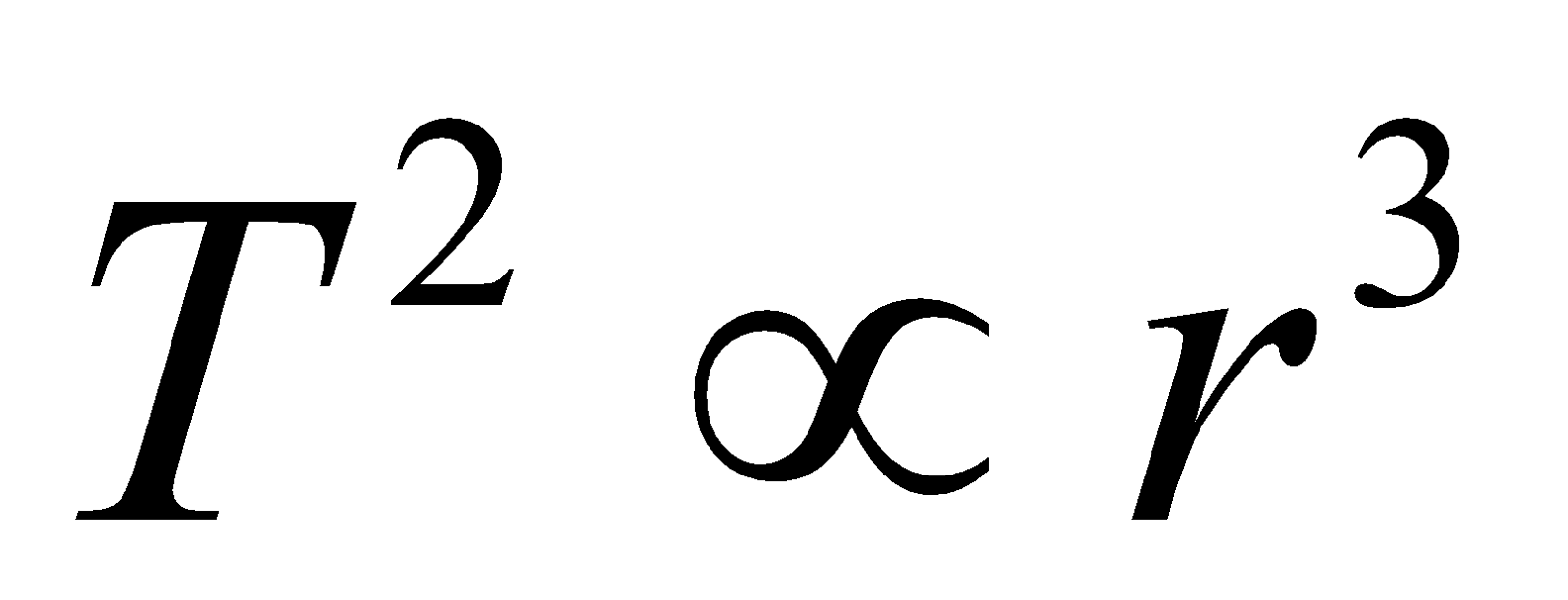
- Maximum number of spectral lines that can be emitted when an electron jumps from nth orbit is
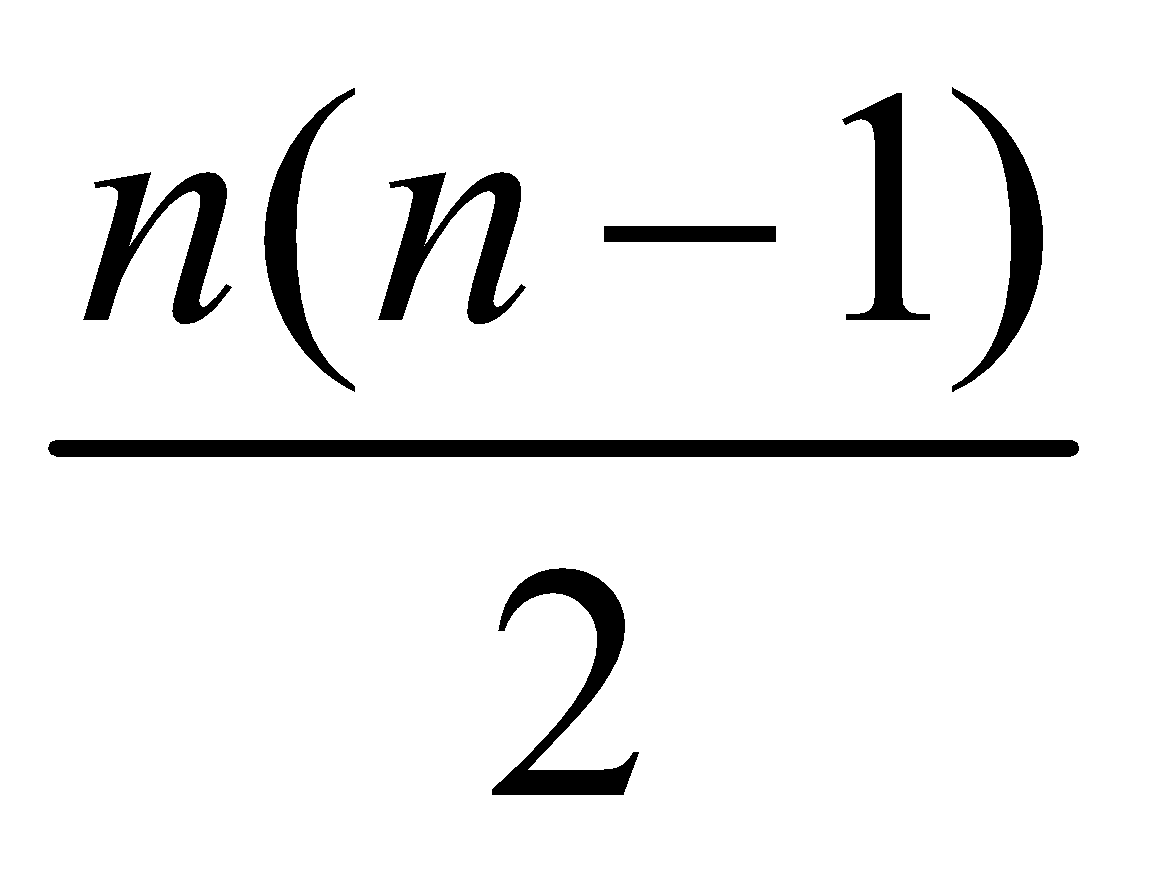
ENERGY LEVELS AND THE LINES SPECTRA OF HYDROGEN ATOM
An energy level diagram of the hydrogen atom is shown in figure. The upper most level corresponding to n→ \(\infty \) , represents the state for which the electron is completely removed from the atom.
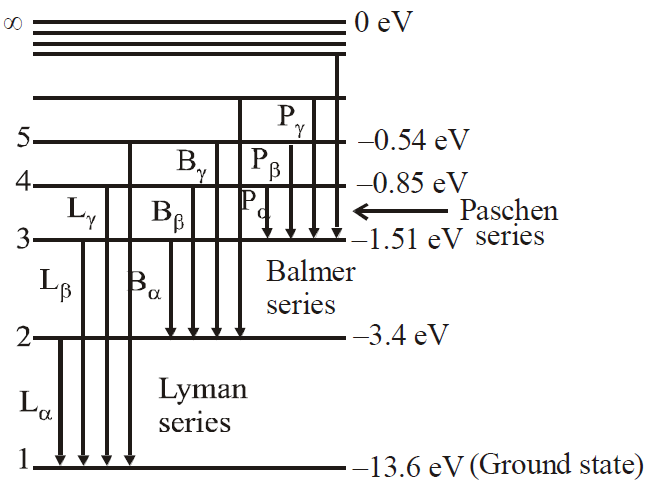
Some transitions for Lyman, Balmer & Paschen series are shown. The quantum numbers are at left & energies of levels are at right.
E = 0 for r = (Since n =
(Since n =  )
)
If the electron jumps from allowed state ni to allowed state nf, then frequency of emitted photon is given by
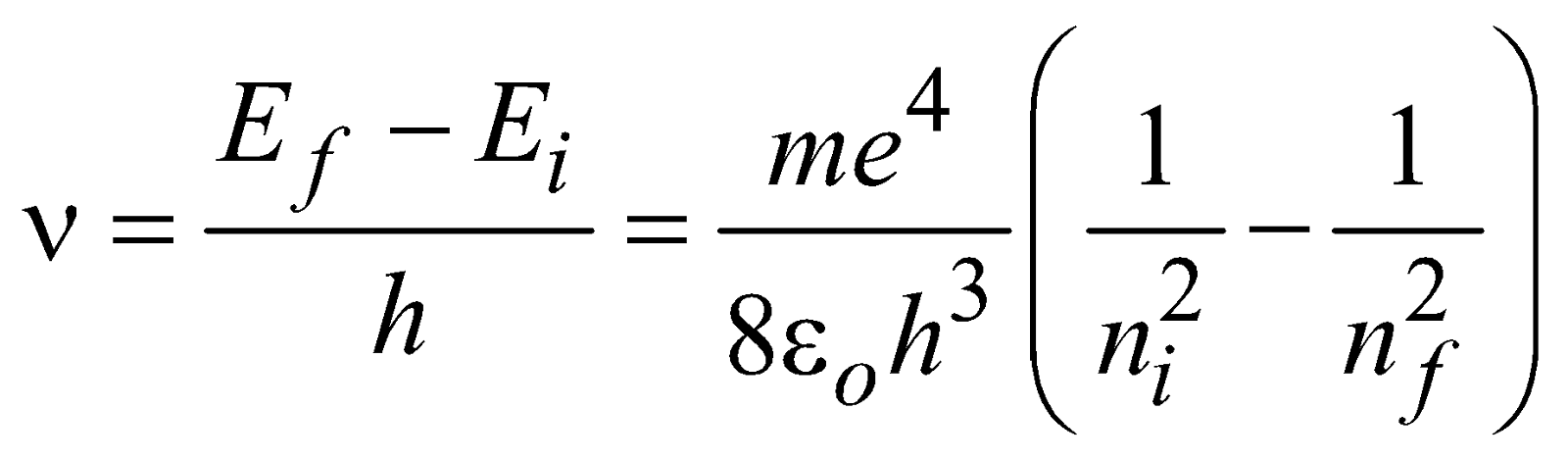 …(1)
…(1)and the wavelength of emitted photon is
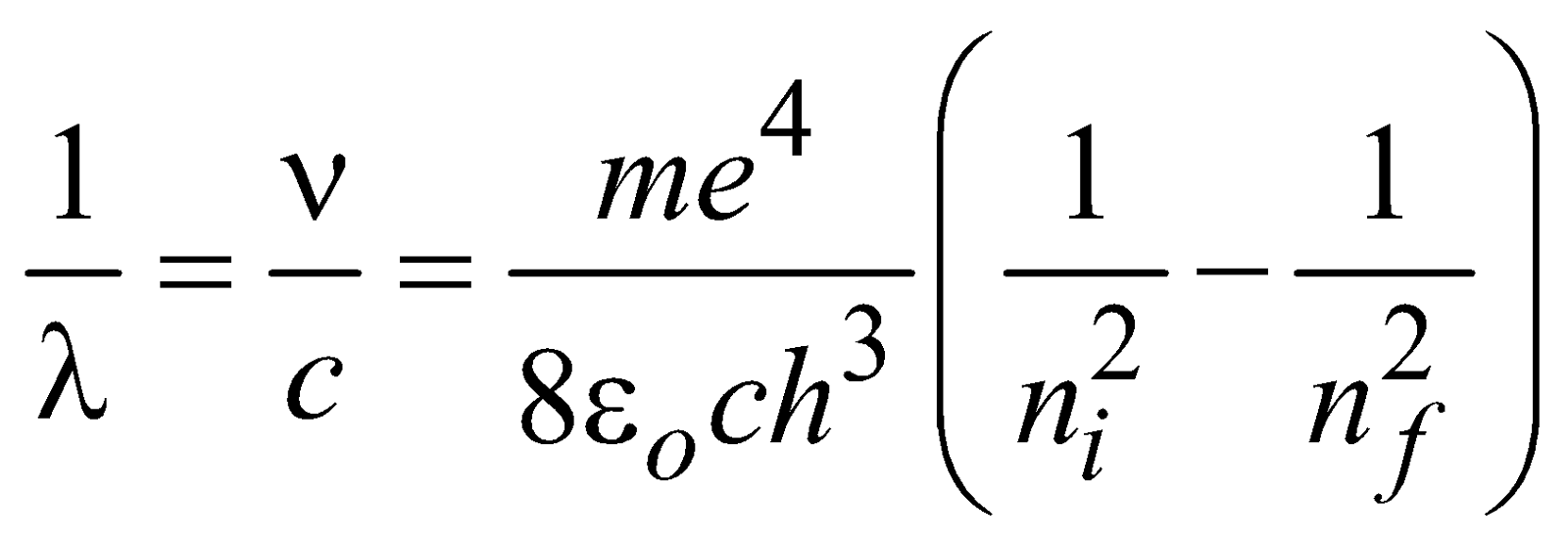
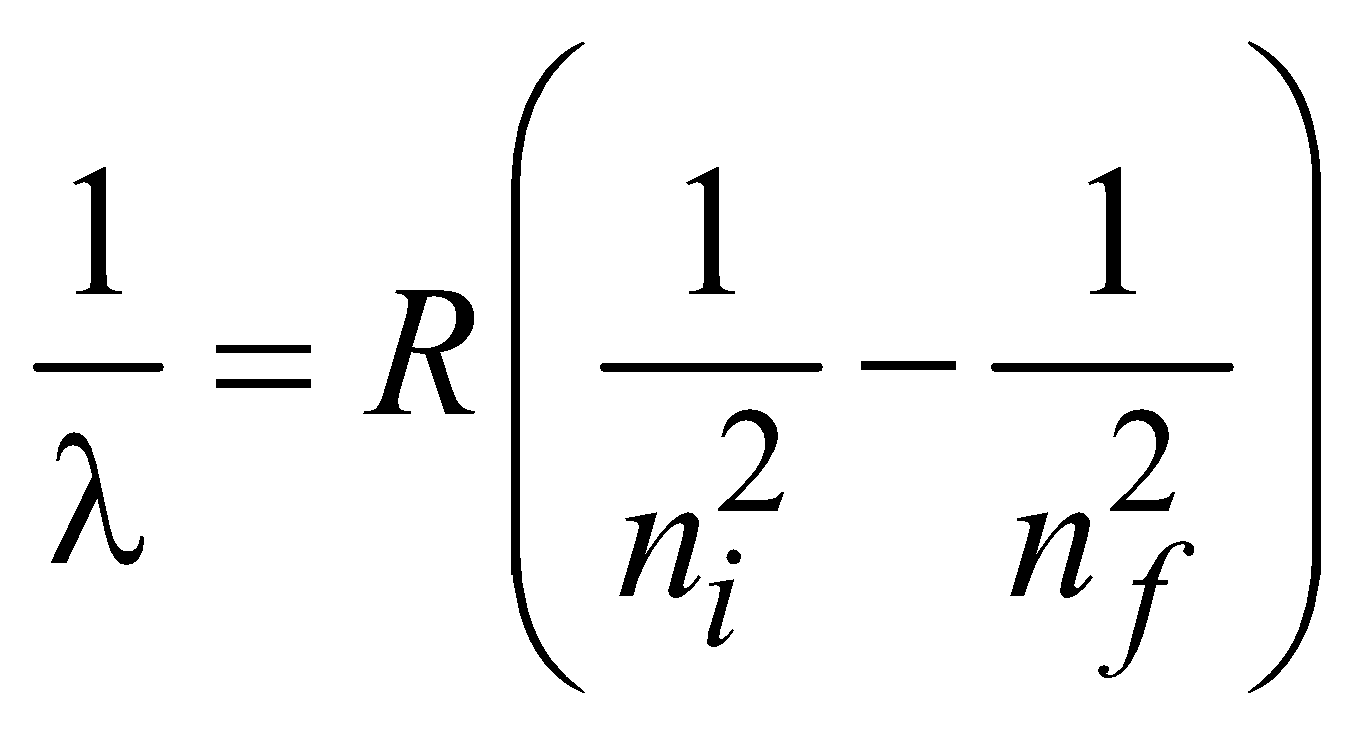 for hydrogen atom …(2)
for hydrogen atom …(2)and 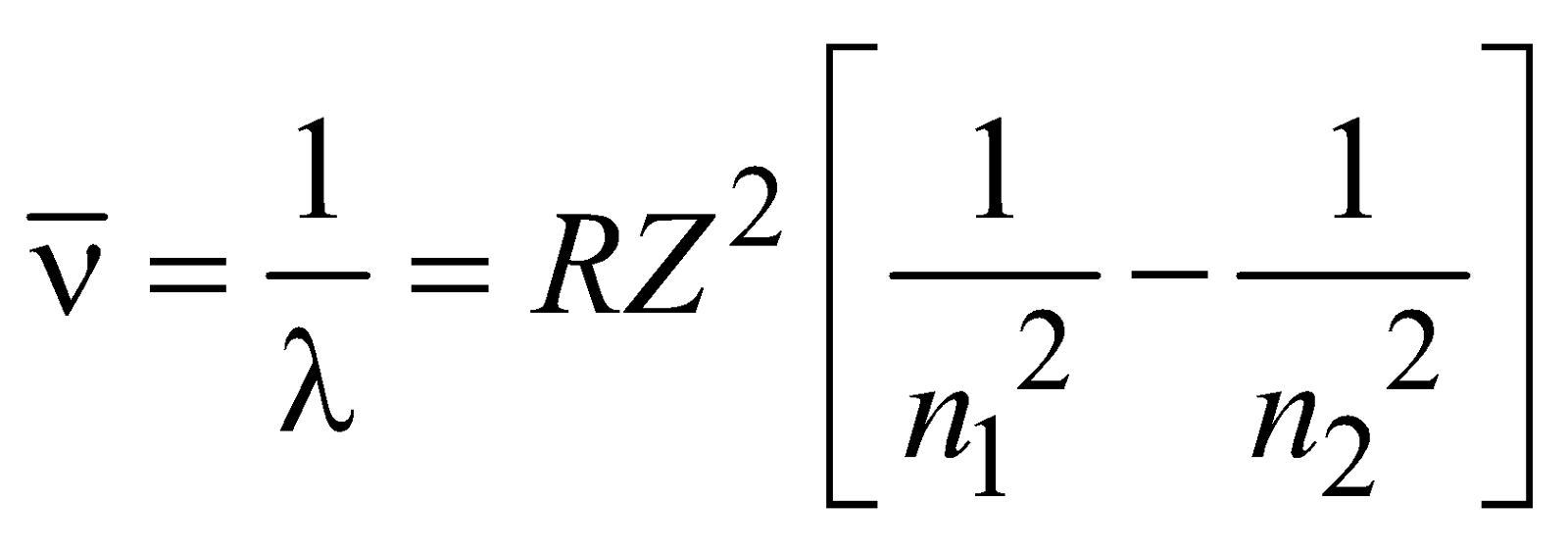 ( for H-like atoms)
( for H-like atoms)
where R = 1.096776 × 107m–1 is known as Rydberg constant. By using this expression we can calculate the wavelengths for various series (Lyman, Balmer…) in hydrogen spectrum, i.e.
- Lyman series ni = 1 & nf = 2, 3, 4……………
- Balmer series ni = 2, & nf = 3, 4, 5……………
- Paschen series ni = 3 & nf = 4, 5, 6…………..
- Brackett series ni = 4 & nf = 5, 6, 7……………
- P fund series ni = 5 & nf = 6, 7, 8……………
First three series of hydrogen atom are shown in figure.
But in practice, the value of Rydberg constant varies between 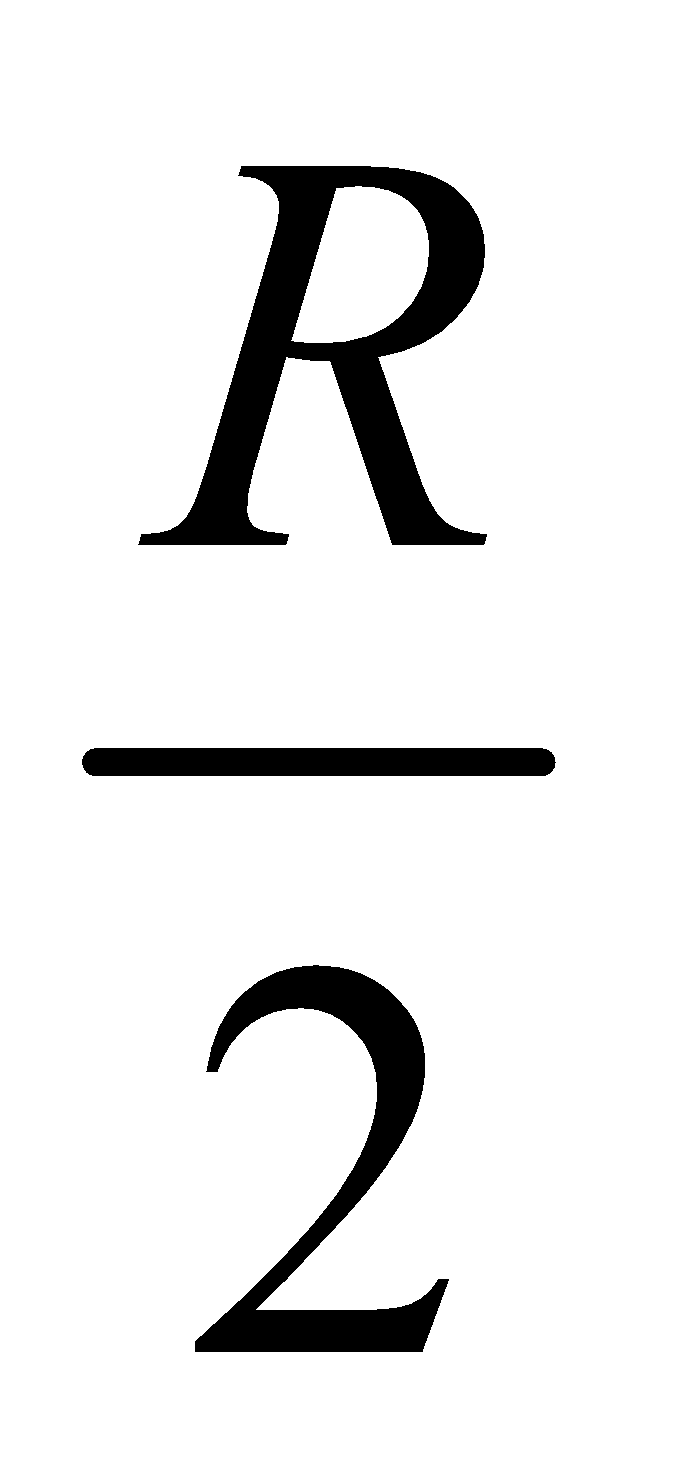 and R
and R
This is because in above calculations we assumed that electron revolves around a massive fixed nucleus of mass M. But in reality, the electron and nucleus each revolve round their common center of mass i.e., the motion of nucleus cannot be ignored. The correction for nuclear motion amounts to replacing electronic mass m by reduced mass μ which is defined as
So total energy by taking this correction is
If we are dealing with hydrogen like ions such as – He+, Li2+, Be3+, Be4+ (one electron ions), each can be considered as a system of two charges, the electron of mass m & charge –e & nucleus of mass M and charge +Ze, where Z is atomic number. The radii of circular orbits for these one electron ions can be written as
and the allowed energies are given by
WAVELENGTH LIMITS IN VARIOUS SPECTRAL SERIES OF HYDROGEN ATOM
- For Lyman series (lies in ultraviolet region)
Here 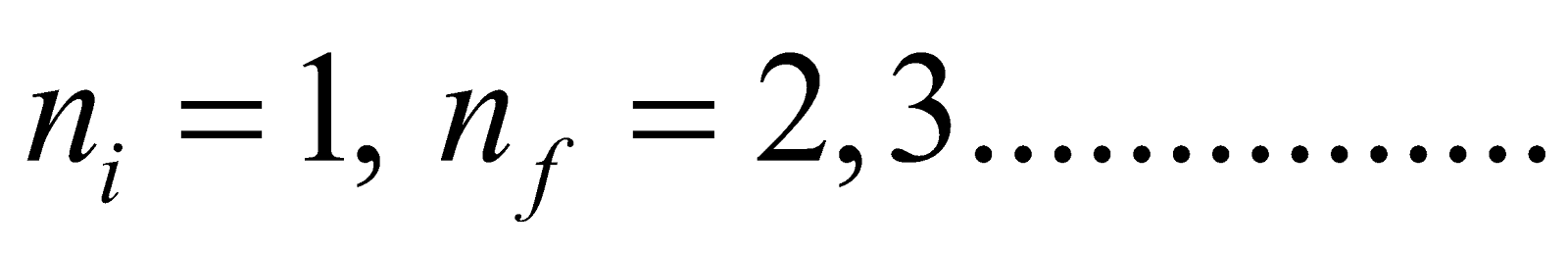
- For Balmer series (lies in visible region)
Here 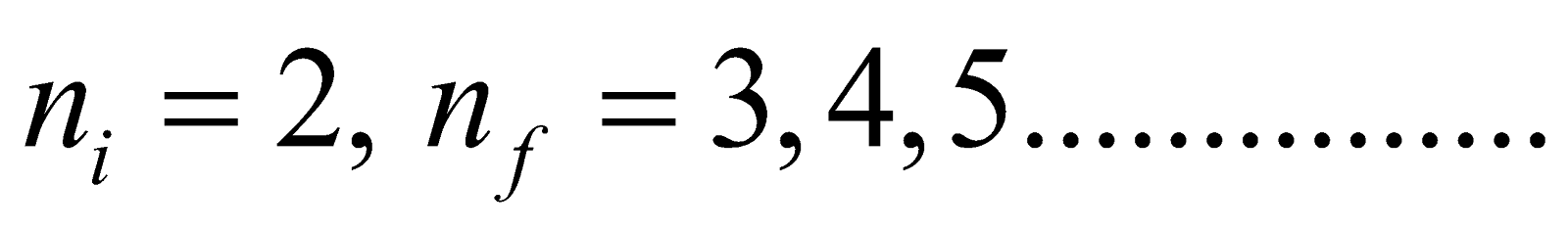
- For Paschen series (lies in infrared region)
Here 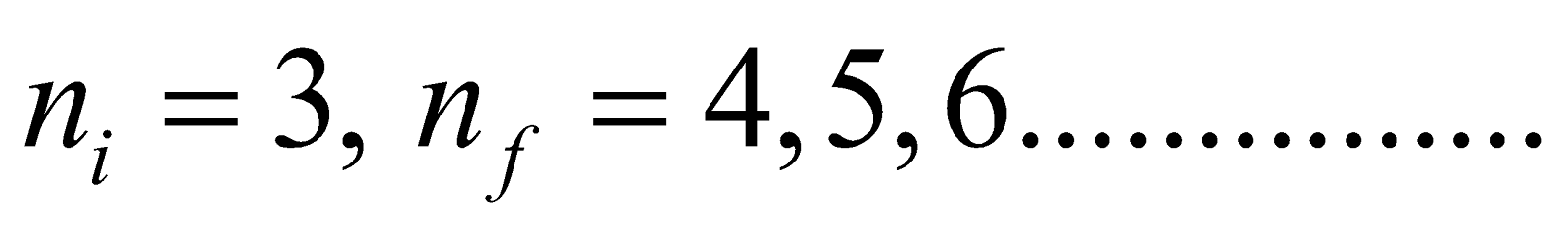
- For Brackett series (lies in infrared region)
Here 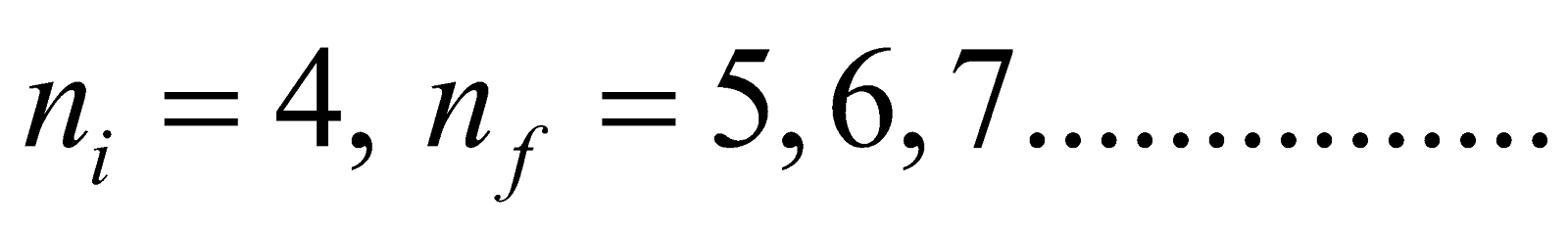
- For p-fund series (lies in infrared region)
Here
KEEP IN MEMORY
- The first line of Lyman series is when electron jumps from 2 → 1, It is also called α–line
The second line of lyman series is when electron jumps from 3 → 1, It is also called β–line
The limiting line of lyman series is when electron jumps from ∞ → 1
- Energy of electrons in different orbits in an atom varies inversely with the square of the number of orbits. So, energy of electrons increases (decreases in negative) as the orbit becomes higher.
- If energy of a particular orbit is E for H-atom then its value for a H-like atom with atomic number Z is given by E’ = E × Z2.
- If the radius of a particular orbit of H-atom is R then its value for a H-like atom is given by
- If velocity of an electron in a particular orbit of H-atom be v then its value for H-like atom is given by
v’= v × Z.
- If kinetic energy and potential energy of an electron in a particular orbit of H-atom be T and V respectively then their corresponding values for H-like atom are given by
T’ = T × Z2 and V’ = V× Z2.
COMMON DEFAULT
🗶 Incorrect. Bohr’s formula for spectral lines does not differentiate between isotopes. For example the first line of Lyman series in hydrogen and deuterium will have same wavelength because
✔ Correct. The value of R will be different for hydrogen and deuterium and therefore λ will be different for the two cases. In fact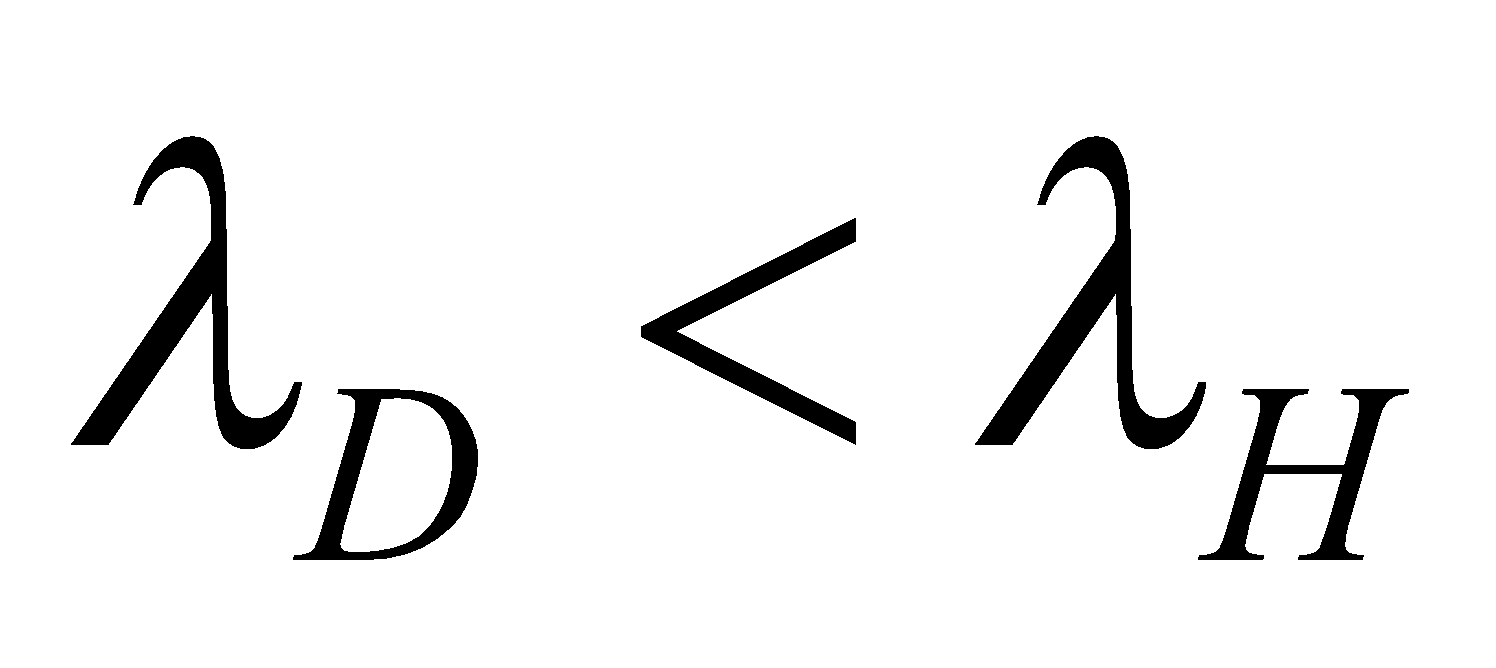
NUCLEI
SOME IMPORTANT FACTS ABOUT ATOMIC MASS, SIZE AND COMPOSITION OF NUCLEUS
- Proton was discovered by Goldstein
- Atomic mass unit
1.a.m.u = 1/12th of mass of C-12 isotope,
1 a.m.u = 1.660565 × 10–27 kg - Mass of a proton, mp = 1.0073 a.m.u = 1.6726 × 10–27 kg
- Chadwick’s experiment
Neutrons were detected.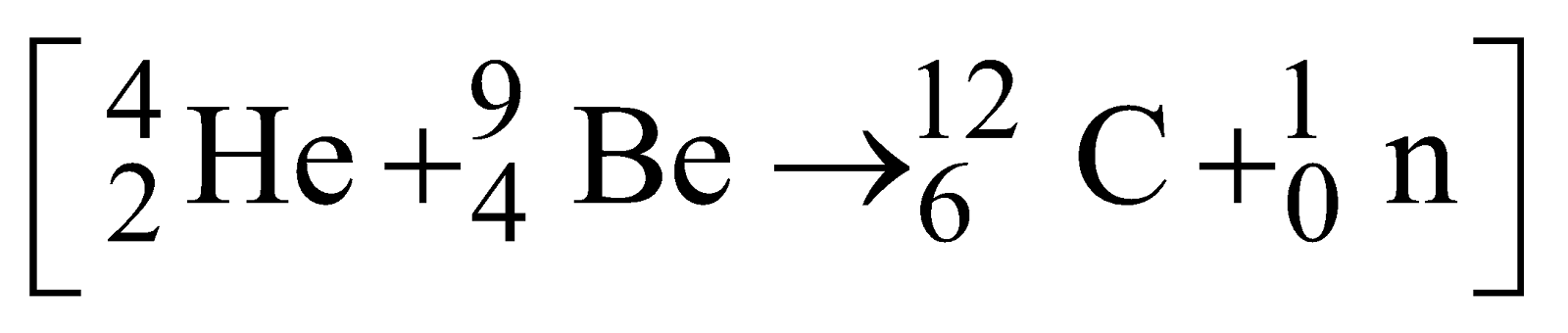
- Mass of neutron, mn = 1.00866 a.m.u = 1.6749 × 10–27 kg
- Mass of electron = 9.1 ×10–31 kg
- Mass number, A = total number of nucleons (neutrons + protons present in the nucleus of an atom)
- Atomic number, Z = number of protons = number of electrons
- Types of nuclei :
- Isotopes : The atoms of the element which have the same atomic number but different atomic mass numbers. e.g., 1H1, 1H2, 1H3 ; 8O16, 8O17, 8O18
- Isobars : The atoms of differents element which have the same atomic mass number but different atomic numbers. e.g., 6C14, 7N14, 18Ar40, 20Ca40 etc.
- Isotones : The nuclides which contain the same number of neutrons e.g., 2H23, 2He24, 2Be59, 5Be510 etc.
- Isomers : having same mass number, same atomic number but different radioactive properties.
- Rest mass of nucleus is less than sum of rest masses of constituent nucleons, the difference is called mass defect.
- Size of the nucleus : Radius of nucleus, R = R0 A1/ 3 where R0 = 1.1 × 10–15 m.
- Nuclear density of all elements ~ 1017 kg m–3.
MASS ENERGY AND NUCLEAR BINDING ENERGY
Einstein’s mass energy equivalence i.e., E = mc2 gives :
and 1MeV = 1.6 × 10–13 J
BINDING ENERGY
Binding energy of a nucleus is the energy with which nucleons are bound in the nucleus. It is measured by the work required to be done to separate the nucleons an infinite distance apart from the nucleus, so that they may not interact with one another.
Total 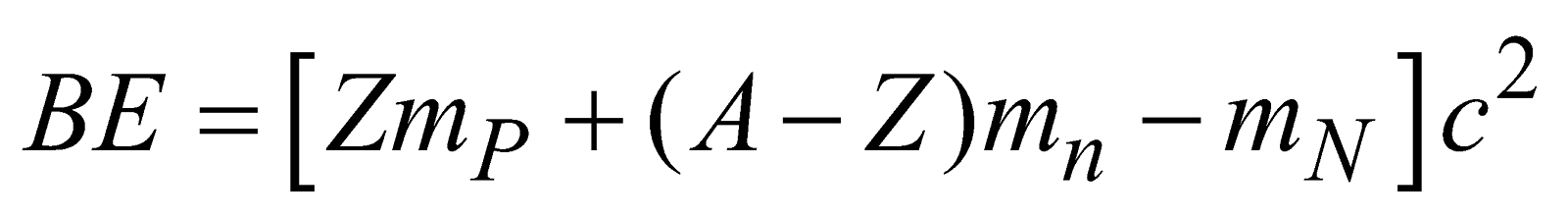
mp = mass of proton; mn = mass of neutron
mN = mass of nucleons (protons + neutrons)
Z = Atomic number
A = atomic mass
Binding Energy per Nucleon
The binding energy per nucleon of a nucleus is the average energy required to extract a nucleon from the nucleus.
Binding energy per nucleon
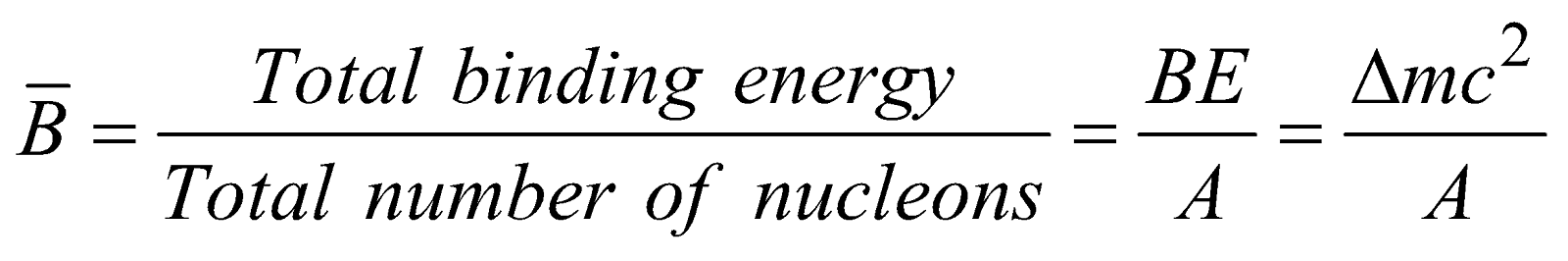
The graph of binding energy per nucleon with mass number A is as shown below.
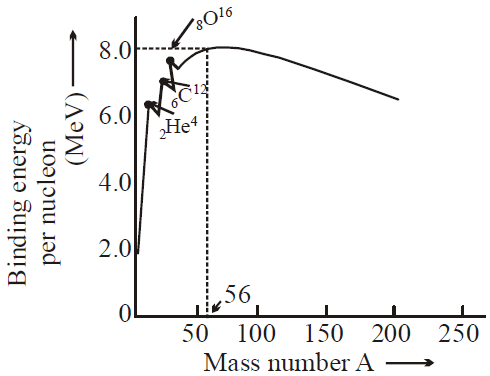
Binding energy per nucleon gives a measure of stability of nucleus. More is binding energy per nucleon more is the stability of nucleus. Binding energy per nucleon is small for lighter nuclei
i.e. 1H1, 1H2 etc.
For A < 28 at A = 4n the curve shows some peaks at 2He4, 4Be8, 6C16, 8O16, 10Ne20, 12Mg24 .
This represents extra stability of these elements with respect to their neighbours.
KEEP IN MEMORY
- A nuclide is a specific nucleus of an atom characterised as ZXA where A = mass number and Z = atomic number.
- Binding energy per nucleon is nearly 8.4 MeV for nuclei in the range of mass number 40 to 120.
- Binding energy is highest in Fe56.( 8.8 MeV)
- Binding energy curve predicts :
- Fission : Breaking up of a heavy nucleus (A > 200) into two nuclei of approximately equal size, and release of energy.
- Fusion : Lighter nuclei ( A < 20) combine together to form heavier nucleus and release of energy.
- BE/ A varies by less than 10% above A = 10 suggests that each nucleon interacts with its neighbouring nucleon only.
- For A > 56, BE/A decreases because of the destabilising effect of long-range coulombic force.
NUCLEAR FORCE
It is the force acts in the nucleus between the nucleons and is responsible for binding the nucleon.
CHARACTERISTICS OF NUCLEAR FORCE
- It is a short range force effective only in range 10–15 m
- It is charge independent. It acts between proton-proton, proton-neutron and neutron – neutron.
- It is not a central force.
- It is spin dependent.
- It is 1038 times stronger than gravitational force and 102 times stronger than electric force.
- The main cause of nuclear force is the exchange of π− mesons between nucleus
RADIOACTIVITY
It is the spontaneous disintegration of the heavy nucleus of an atom. It occurs without external provocation.
There are three main types of radioactive radiations.
- α-rays (i.e., Helium nuclei or α – particles)
- β-rays (i.e., electron or positron or β – particles)
- γ-rays (photons or gamma radiations)
It is a process by which an unstable nuclei achieves stability. This process is not affected by
- chemical combination
- changing physical environment other than nuclear bombardment
FEATURES OF RADIOACTIVITY
- It is a statistical process.
- When a nucleus undergoes alpha or beta decay, its atomic number and mass number changes (in β-decay only atomic number changes) & it transforms into a new element.
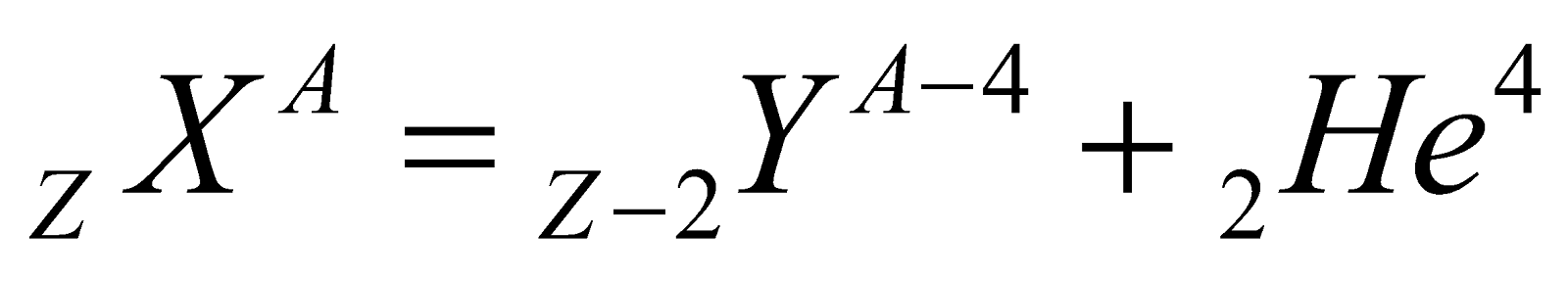 (α-particle), it means that by emission of alpha particle (α-particle), it loses 2 units of charge and 4 units of mass.
(α-particle), it means that by emission of alpha particle (α-particle), it loses 2 units of charge and 4 units of mass.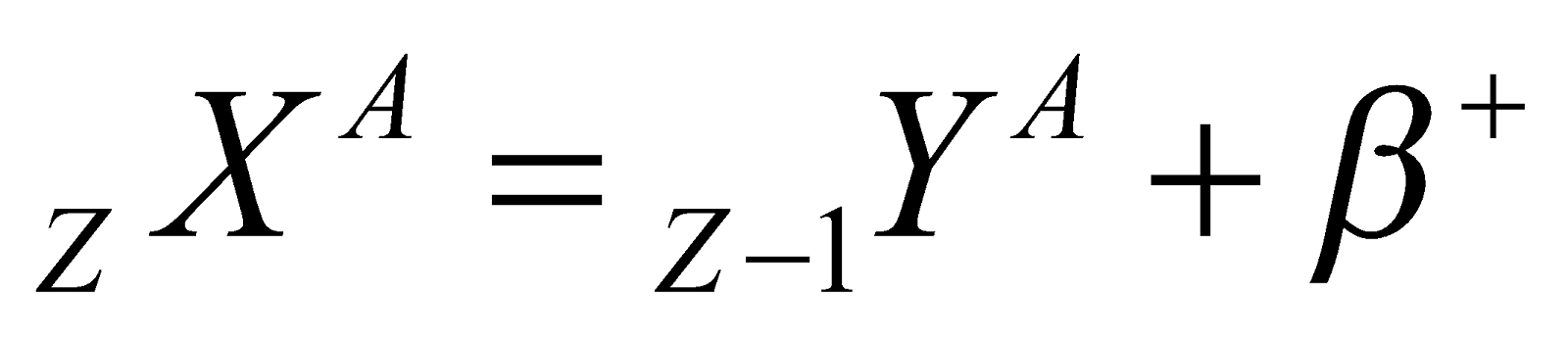 (positron). It means that by emission of beta particle (β+-particle), nucleus loses one unit of charge. It is surprising to note that a nucleus does not contain β+ then how is it emitted. Reason : During a β+ particle(i.e., positron) decay, a protron converts into a neutron
(positron). It means that by emission of beta particle (β+-particle), nucleus loses one unit of charge. It is surprising to note that a nucleus does not contain β+ then how is it emitted. Reason : During a β+ particle(i.e., positron) decay, a protron converts into a neutron
A β– particle (i.e., electron) decays, when inside the nucleus a neutron converts into a proton i.e.,
Since β−particle is an electron (or positron), so the loss of mass in this decay is negligible.
In β+decay the daughter element is one place forward in the periodic table.
- When a nucleus emits a gamma ray, neither the mass nor the charge of the nucleus changes
i.e., 
The gamma ray(γ-ray) is photon & it carries away some energy from the nucleus & nucleus returns from excited state(unstable state) to ground state (stable state)
α and β-particles are not emitted simultaneously.
γ rays are emitted after the emission of α and β-particle. α, β and γ-rays are known as Becquerel rays.
The energy spectrum in the case of β-particles is continuous but that of α and γ-rays is a line spectrum. This means that β particles are emitted with any amount of kinetic energy.
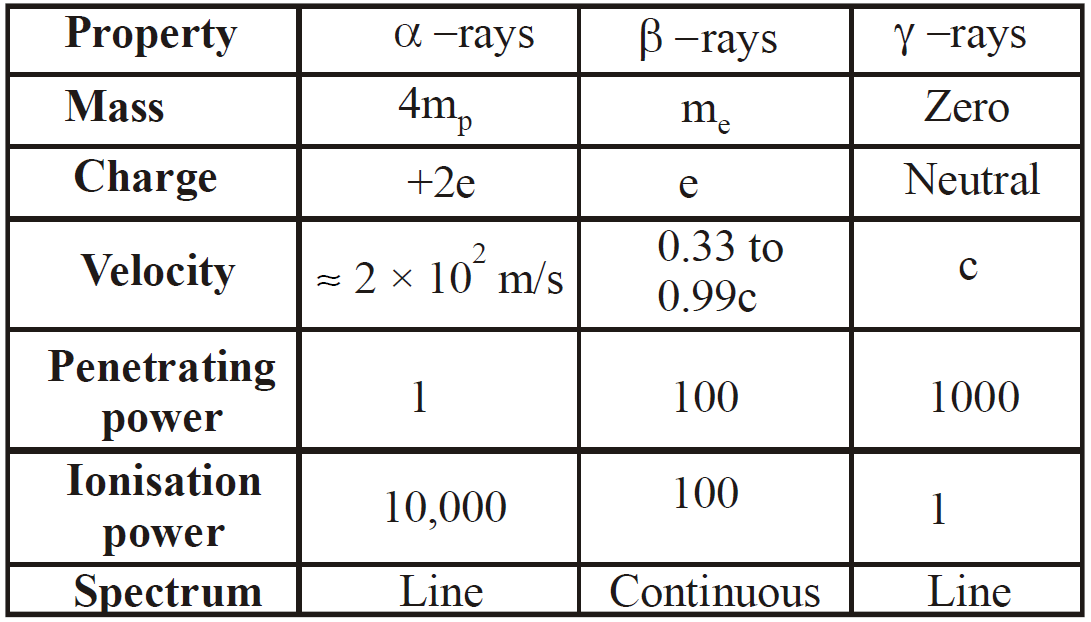
PROPERTIES OF α, β & γ-RAYS
(A) PROPERTIES OF α−RAYS
- It is a positively charged particle & contains a charge of 3.2 × 10–19 coulomb (exactly double the charge of electron).
- The mass of α-particles is 6.645 × 10–27kg (It is equal to mass of a helium nucleus). Actually α-particle is nucleus of helium, hence it is called doubly ionised helium.
- They (α-particles) get deflected in both electric & magnetic fields.
- The velocity of α-particle is very less than the velocity of light i.e.,
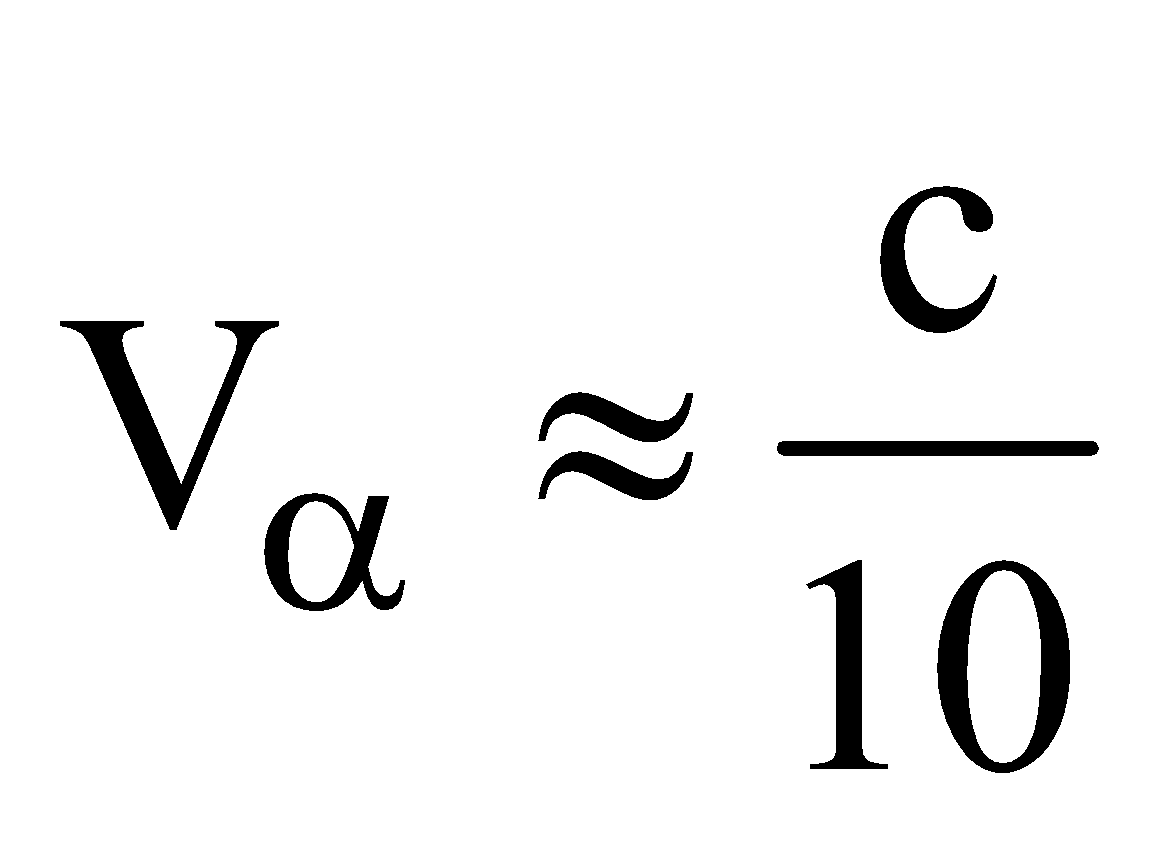 , where c is velocity of light.
, where c is velocity of light. - The range of α-particle in air depends on radioactive substance.
- The ionisation power of α-particle is higher than both β (100 times of β & 10,000 times of γ) and γ particle.
- The penetrating power of α particle is lowest (in comparison to β & γ particles). It is 1/100 times of β-particles & 1/10,000 times of γ-rays.
- The α-particles can produce fluorescence in barium platinocyanide and zinc sulphide.
- They show little effect on photographic plate.
- They show heating effect on stopping.
(B) PROPERTIES OF β-RAYS OR β-PARTICLES
- The beta particles (i.e., β– or β+) may be positive & negative particle & contain
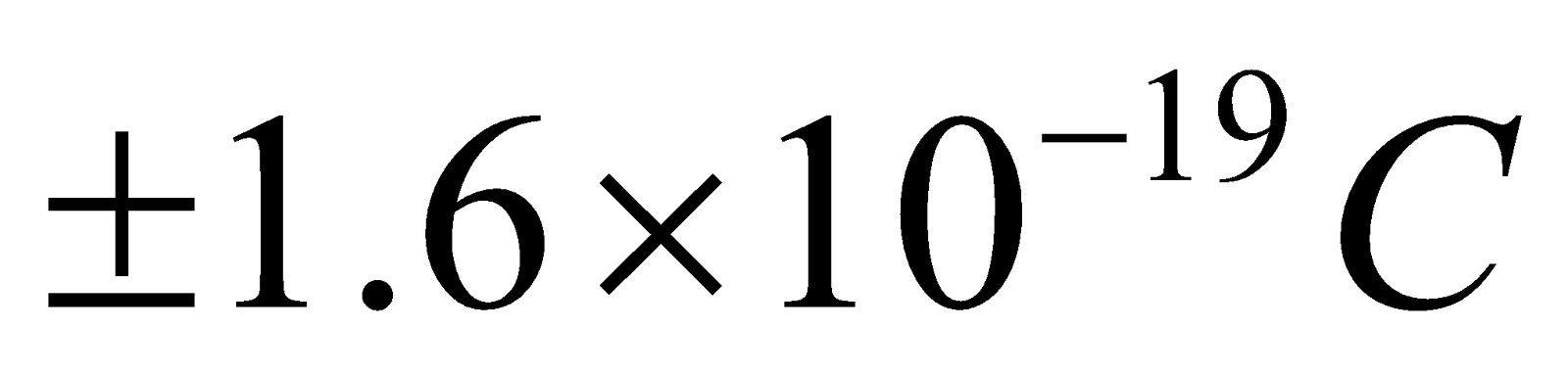 of charge. Actually β– is electron & β+ is positron.
of charge. Actually β– is electron & β+ is positron. - They get deflected in both electric & magnetic field.
- The velocity of β-particle varies between 0.01c to .99c, where c is velocity of light.
- The mass of β particle is relativistic, because its velocity is comparable to velocity of light
- They have both ionisation & penetration power. Ionisation power less than α-particle and penetration power more than α-particle.
- They produce fluorescence on barium platinocyanide & zinc sulphide.
(C) PROPERTIES OF γ-RAYS (OR GAMMA RADIATION)
- They are electromagnetic waves as x-rays.
- They are not deflected in electric & magnetic field, it means that they are chargeless.
- The velocity of γ-particle is equal to velocity of light.
- The ionisation power of gamma rays is less than β & α rays but penetration power more than β and α-rays.
- The γ-particles are emitted from the nucleus, while X-rays are obtained, when electron goes from one state to another in an atom.
- When γ-rays photon strikes nucleus in a substance, then it gives rise to a phenomenon of pair production i.e.,
The minimum energy of γ-rays required for this phenomena is 1.02 MeV, because the rest mass energy of 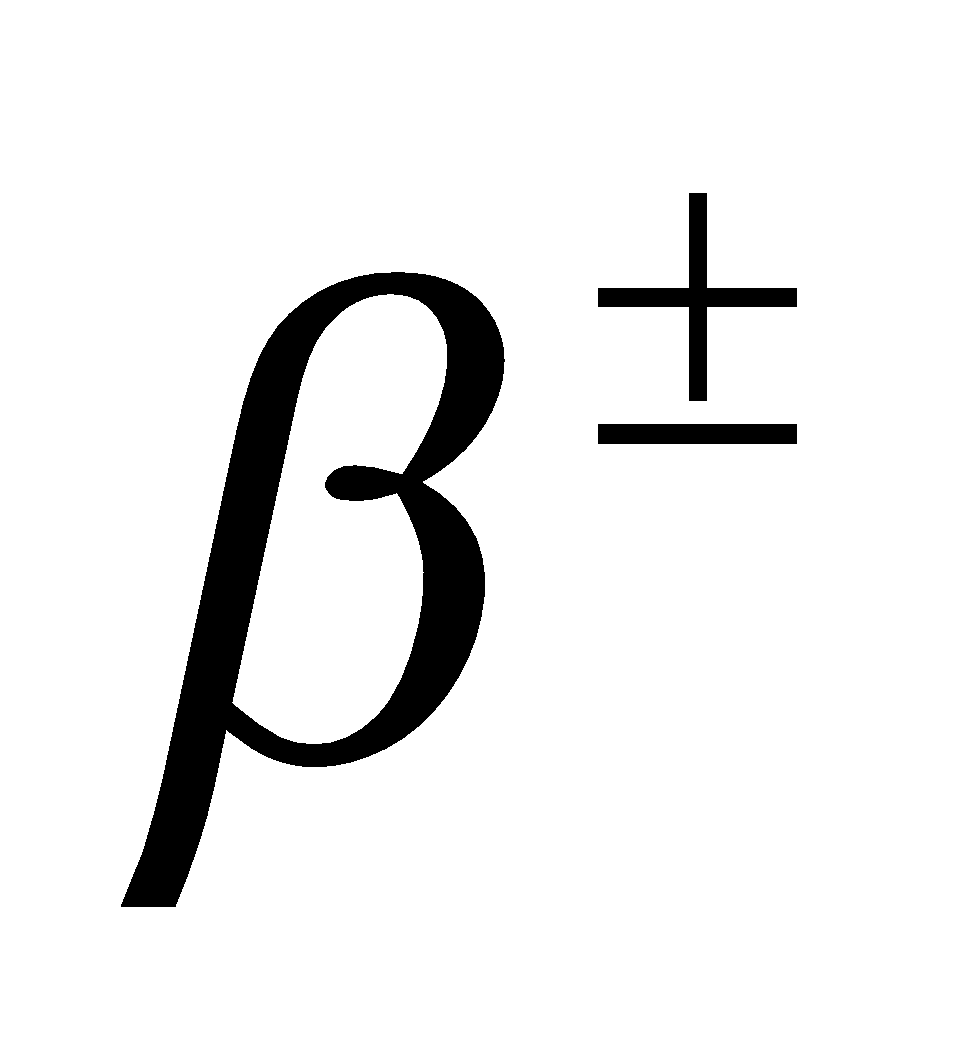 particle is 0.51 MeV.
particle is 0.51 MeV.
RUTHERFORD AND SODDY LAW FOR RADIOACTIVE DECAY
It states that ”at any time the rate at which particular decay occurs in a radioactive substance is proportional to number of radioactive nuclei present.”
If N is the number of nuclei at any time t & at t + dt time, it decrease to N-dN then the rate of decay of these nuclei is 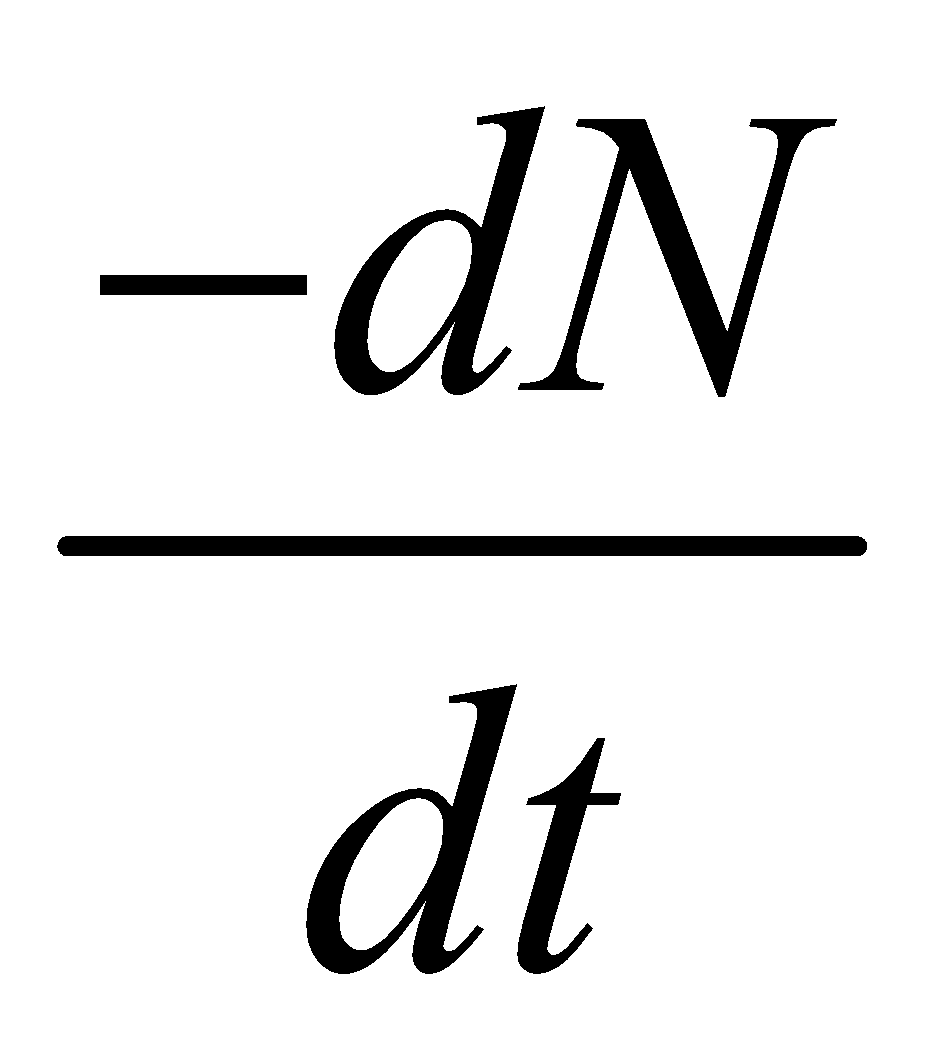 (negative sign comes because N decreases as t increases). So according to Rutherford & Sodi,
(negative sign comes because N decreases as t increases). So according to Rutherford & Sodi,
Where λ is decay constant (i.e., probability per unit time for a nucleus to decay) and it is constant for a particular nuclei, but different for different nuclei. By integration of equation (1) w.r. to time we get
N = No e–λt …(2)
where No is the number of nuclei at t = 0.
Activity : The number of decays per unit time or decay rate is called activity(R)
The S.I. unit of R is becquerel,
1 becquerel = 1 Bq = 1 decay/sec and 1 curie = 1 Ci = 3.7 × 1010 decay/sec
The other unit of radioactivity is rutherford.
1 rutherford = 106 decay/sec
⇒ 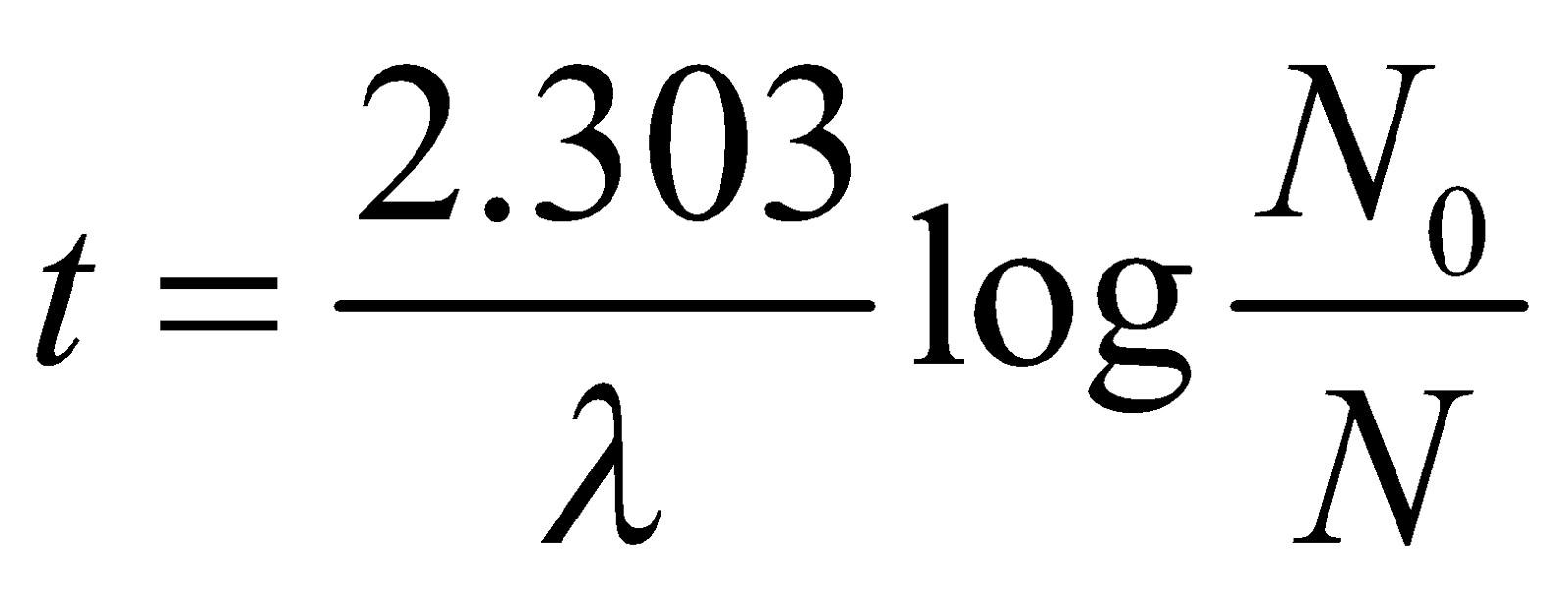
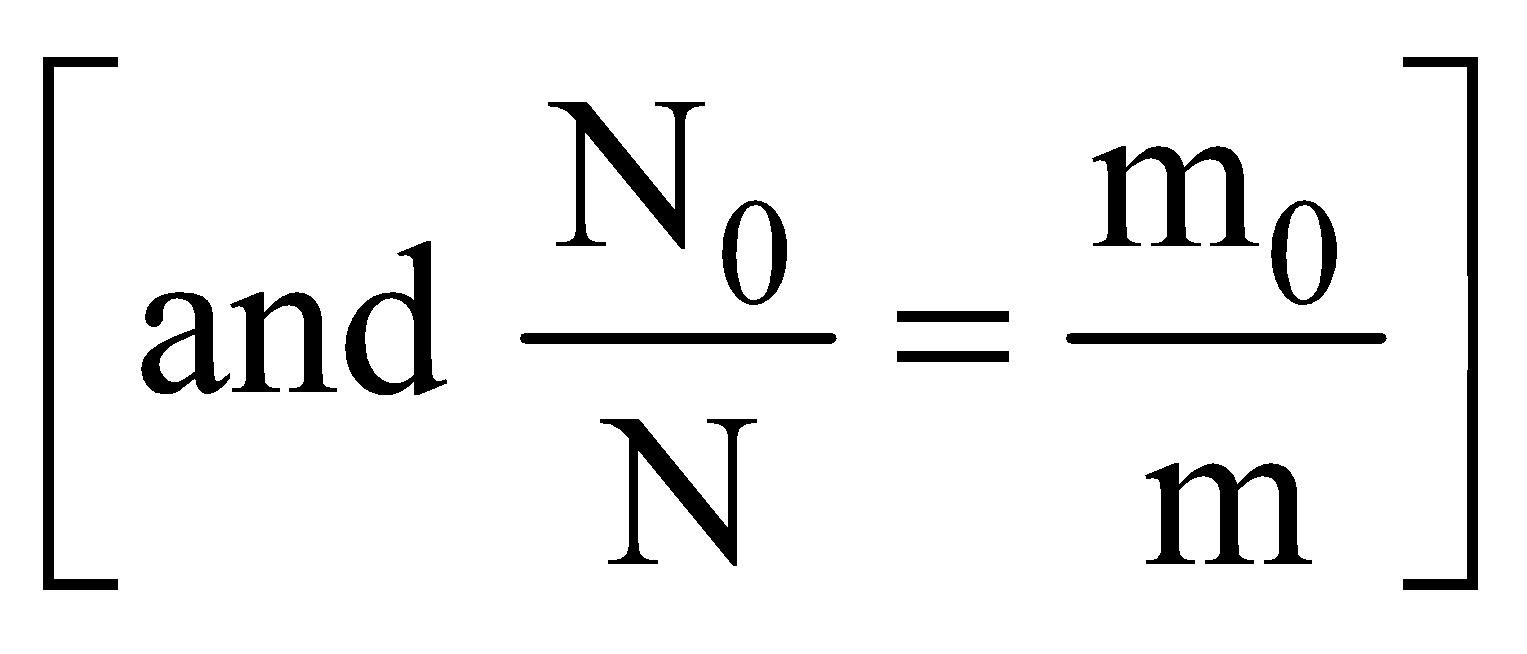
m0 = mass at t =0 and m = mass at t = t
COMMON DEFAULT
🗴 Incorrect. Since β-particles (electrons) are emitted from the nucleus shows that electrons exist in nucleus
✓ Correct. β-particle cannot exists in nucleus. It is created and ejected at once at the time of β-decay. β-particle cannot exist in the nucleus because its wavelength is greater than the size of nucleus
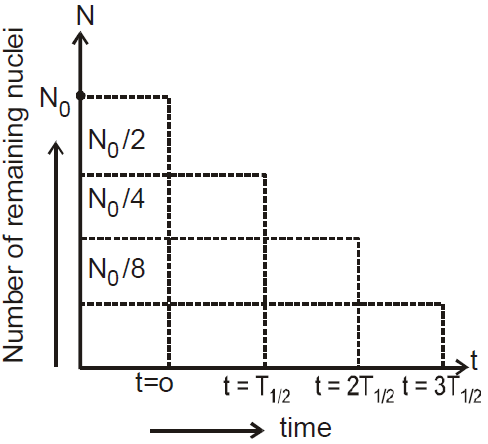
HALF-LIFE OF A RADIOACTIVE SUBSTANCE
Half-life of a substance is the time, it takes for half of a given number of radioactive nuclei to decay
Let at = T1/2
 then by eq. (2)
then by eq. (2)
Also 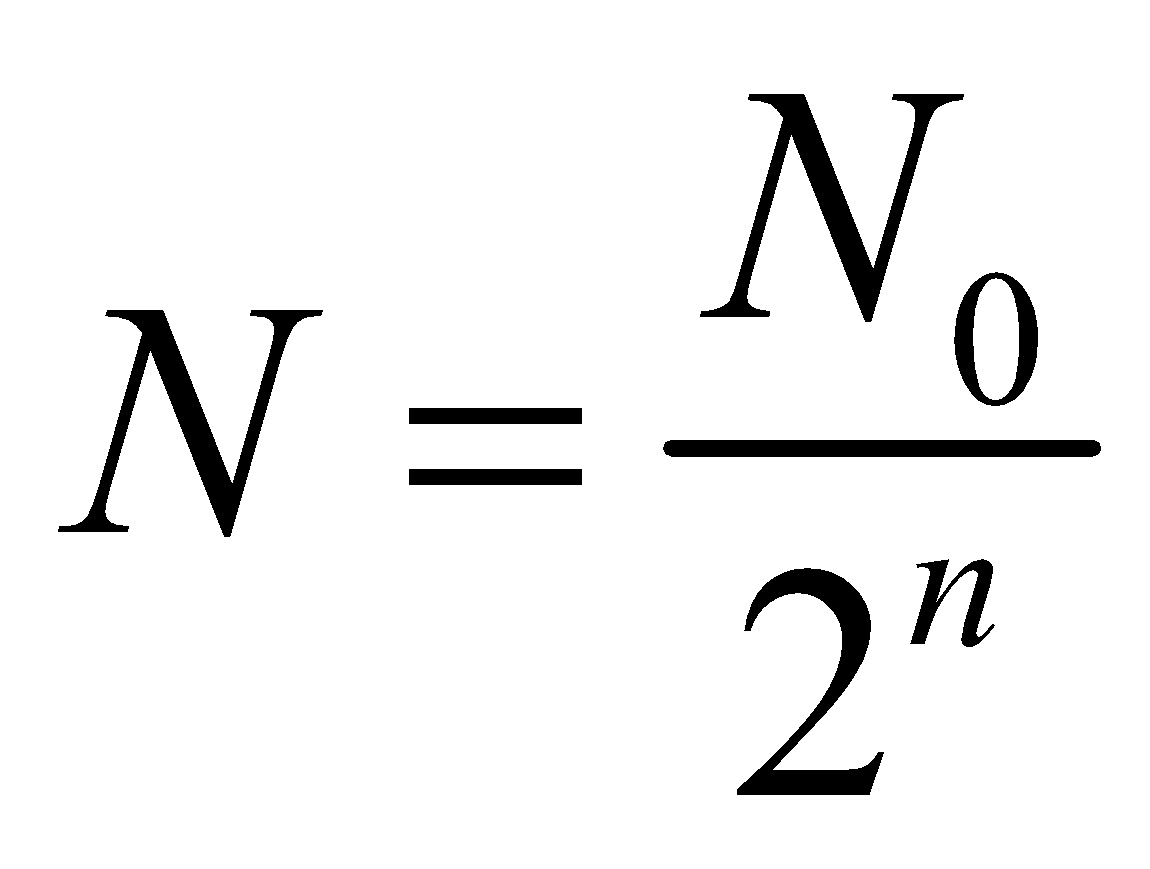 for n half-lives
for n half-lives
⇒  where m0 is mass of radioactive substance at t = 0 and m is mass at t = t.
where m0 is mass of radioactive substance at t = 0 and m is mass at t = t.
MEAN LIFE OF A RADIOACTIVE SUBSTANCE
Mean life (average life) τ is defined as the average time the nucleus survive before it decays.
It is given as : 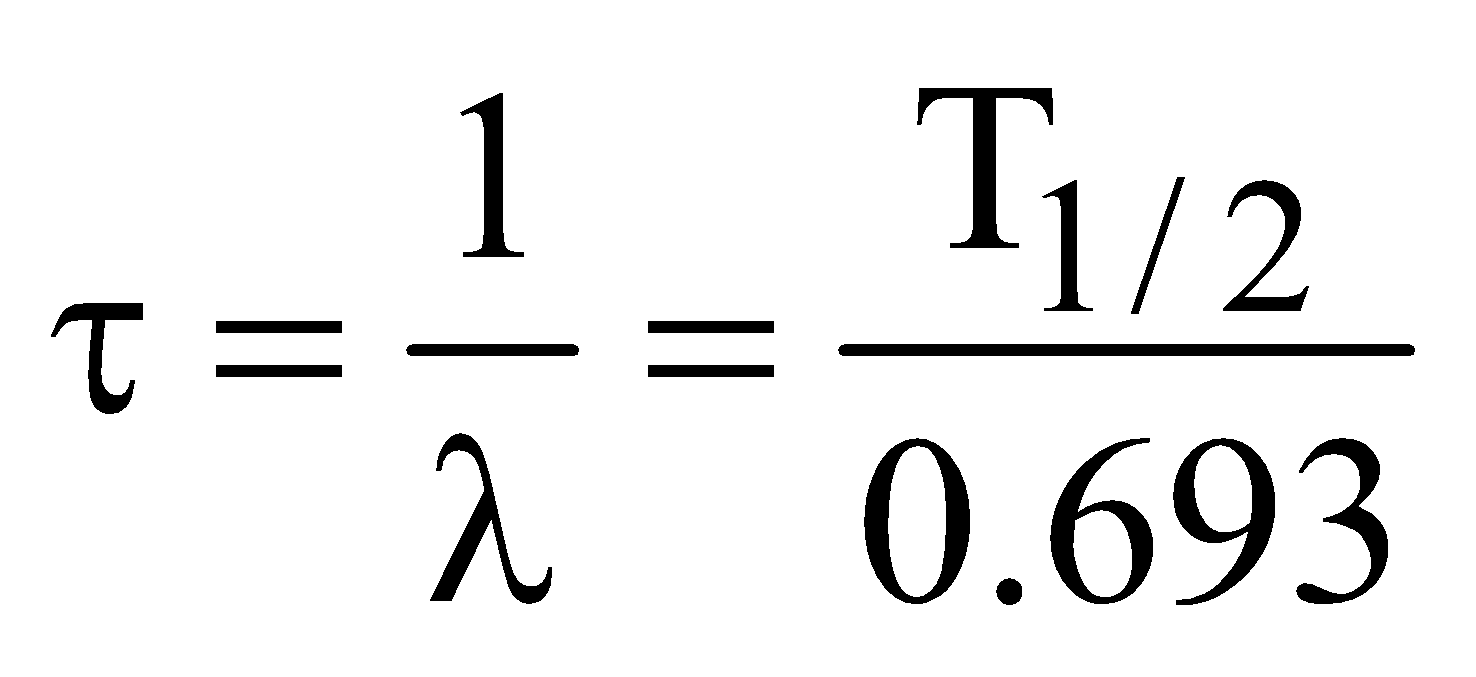
The equivalent  and τ for two nuclei A and B,
and τ for two nuclei A and B,
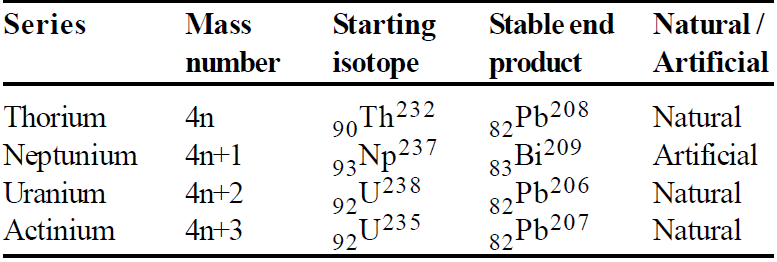
RADIOACTIVE SERIES
The heavy nuclides change their mass number by α decay and atomic number by α and β decay.
They can decay to stable end products by four paths. The four paths have mass numbers given as 4n, 4n + 1, 4n + 2, 4n + 3 where n is integer.
Last element of series is stable and has a decay constant zero.
There are four radioactive series :
Uranium 92U238 → 82Pb206
(Half life 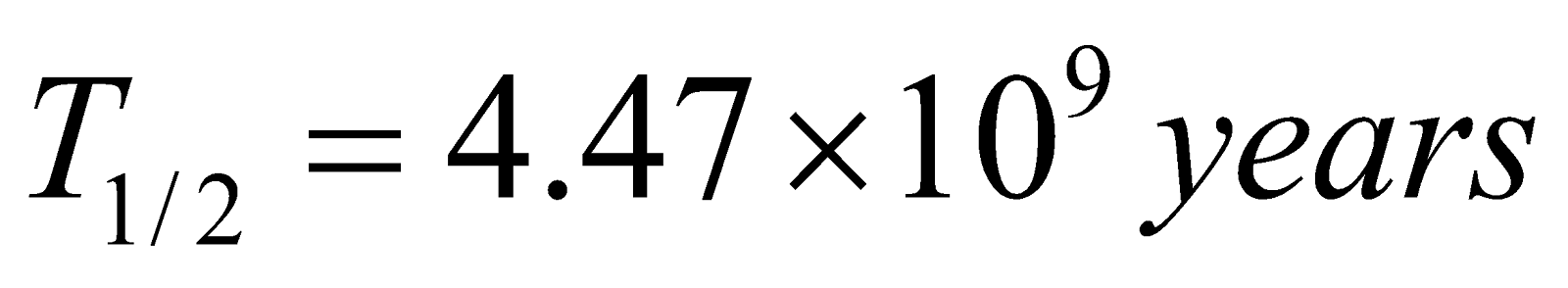 )
)
Actinium (natural) 92U235 → 82Pb207
(Half life 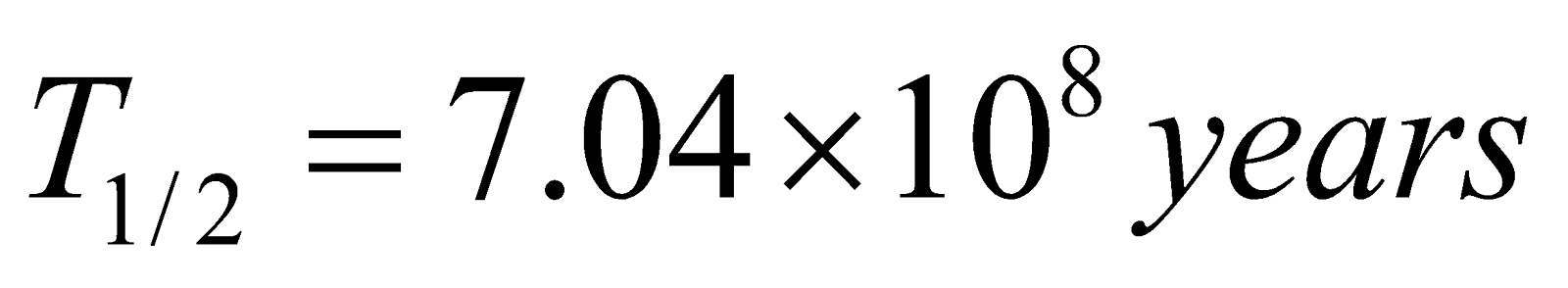 )
)
Thorium 92Th232 → 82Pb208
(Half life 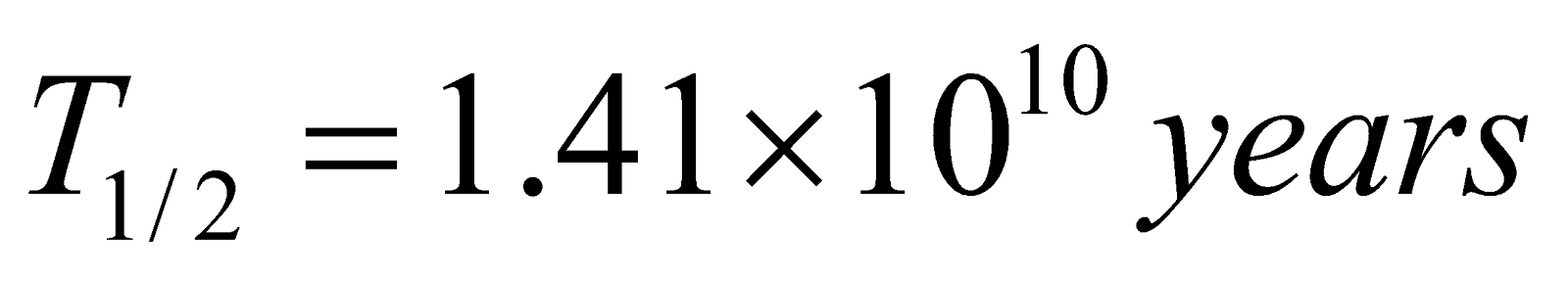 )
)
Neptunium 93Nb237 → 83Bi209
(Half life 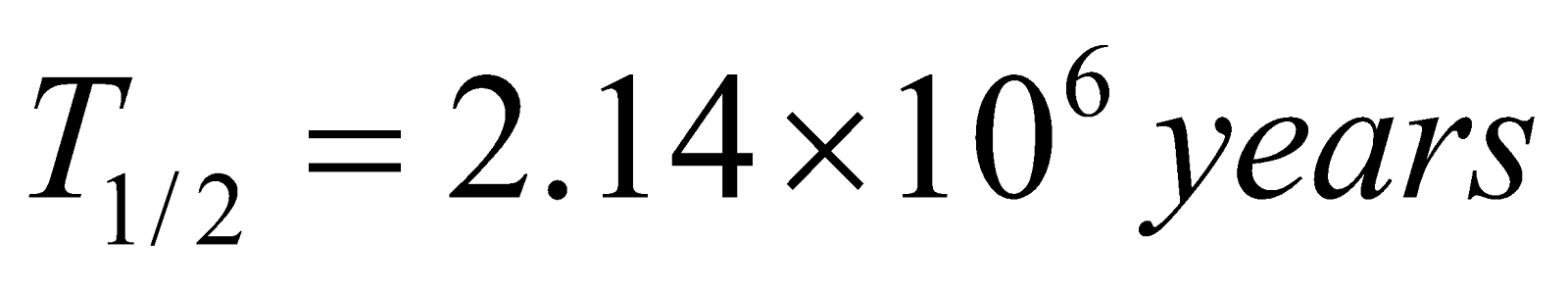 )
)
But only first three series occur in nature & fourth one is artificial.
RADIOACTIVE EQUILIBRIUM
When the rate of formation of daughter nuclei becomes equal to rate of its decay then this is called as state of radioactive equilibrium
NA λA = NB λB = ………… or 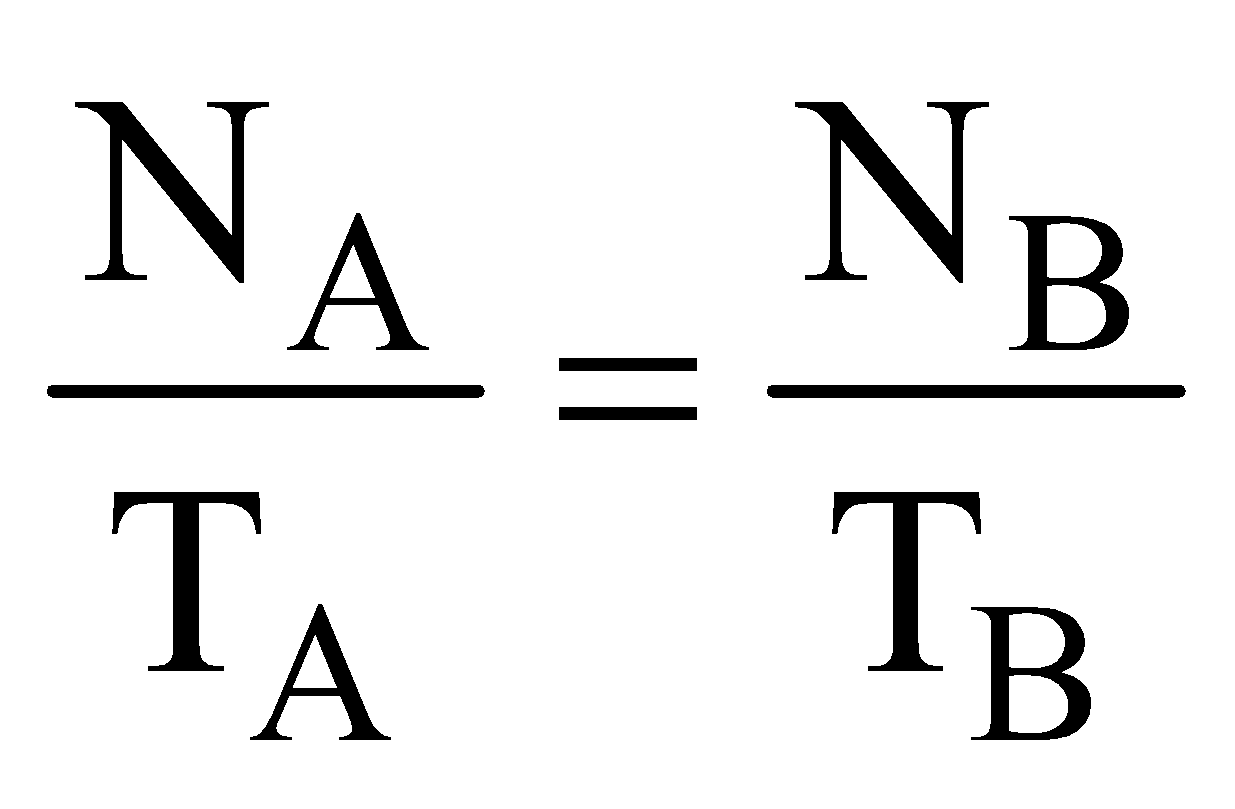 = …………
= …………
CARBON DATING
Carbon dating is the process of determination of time interval which has passed by making use of radioactive decay of a sample containing radioactive substance (6C14). It helps in calculating age of geological specimens like rocks, biological specimens likes bones of animals or trunk of trees and age of earth. The isotope of carbon 6C14 is radioactive. It is formed in atmosphere by bombardment of nitrogen atoms with cosmic rays
7N14 + 0n1 → 6C14 + 1H1
The 6C14 combines with oxygen to form carbon dioxide which is absorbed by plants so concentration of 6C14 is constant with time. The living plants and animals have a fixed ratio of 6C14 to ordinary carbon 6C12. When a plant or animal dies the content of 6C14 decreases while that of 6C12 remains constant. The ratio of two indicates the time that has passed since death of plant or animal. The time interval is calculated from the laws of radioactive disintegration
where No is number of 6C14 nuclei at time of death, λ is decay constant of 6C14 and N is number of 6C14 nuclei currently present in sample.
KEEP IN MEMORY
- Specific activity is the activity of 1 gram of material.
- Geiger Muller Counter is used for detecting α and β particles.
- Cloud chamber is used for detecting radioactive radiations and for determining their paths, range and energy.
- Baryon number
B = 1, for a neutron and a proton. - Lepton number (L)
L = 1 for electron, and neutrino
L = –1 for positron and antineutrino.
- Radioactive isotope
- Iodine-131 For detecting the activity of thyroid gland
- Chromium-51 To locate the exact position of haemorrhage
- Phosphorus-32 In agriculture
- C–14 Carbon dating, Photosynthesis in plants
- Co60 Cancer treatment
- Na24 For circulation of blood
NUCLEAR REACTION
Nuclear reaction obeys following conservation laws :
- Charge conservation
- Conservation of linear momentum
- Conservation of angular momentum
- Conservation of energy (Rest mass energy + K.E.)
Standard way of representing a nuclear reaction
For a nuclear reaction
Standard way 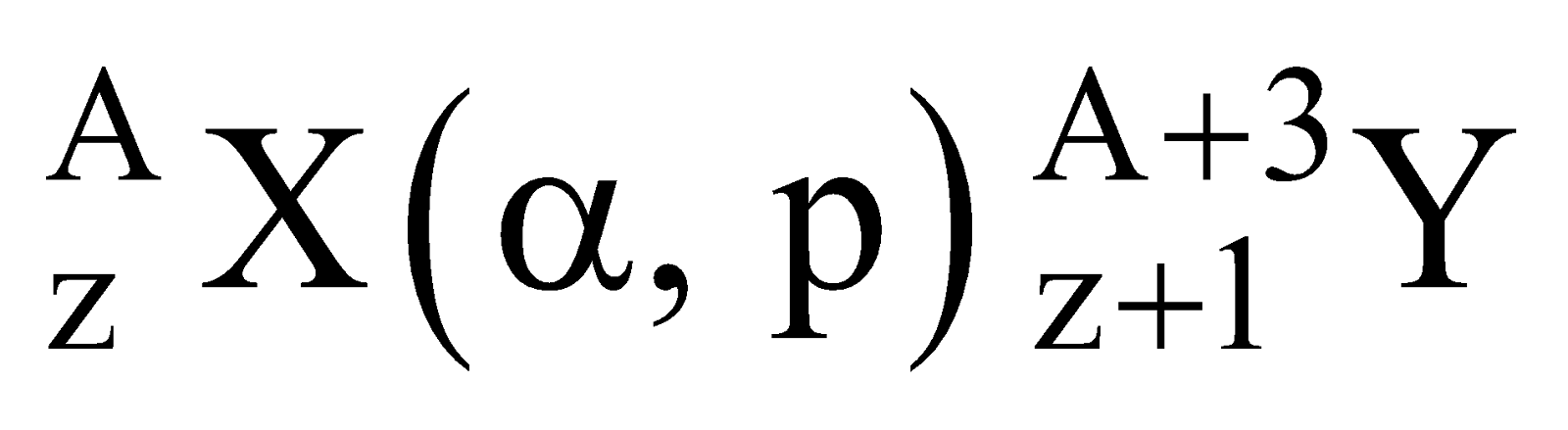
NUCLEAR FISSION (BY OTTO HAHN AND STRASSMANN)
Nuclear fission is the disintegration of a heavy nucleus upon bombardment by a projectile, such that the heavy nucleus splits up into two or more segments of comparable masses with an enormous release of energy.
The most of the energy released is by the mode of kinetic energy of fission segment.
Uncontrolled Chain Reaction : It is the principle of atom bomb (destructive use). The number of fission in this case goes on increasing at a tremendous rate leading to the creation of a huge amount of energy in a very small time.
The number of fissions in this case is maintained constant.
Nuclear reactor has been devised for this purpose.
The main parts of nuclear reactor are
- Nuclear fuel : U233, U235, Pu239 etc.
- Moderator : Graphite, heavy water (D2O). To slow down the neutrons (or slow down the nuclear reaction).
- Control rods : (Cadmium, boron). To absorb excess neutrons. It controls the chain reaction.
- Coolant : (water etc). To remove the heat produced in the core to heat exchanger for production of electricity.
The reaction of controlled chain reactor is also called critical reaction.
Critical mass : It is the minimum amount of fissionable material required to carry out fission reaction. It is 10 kg for 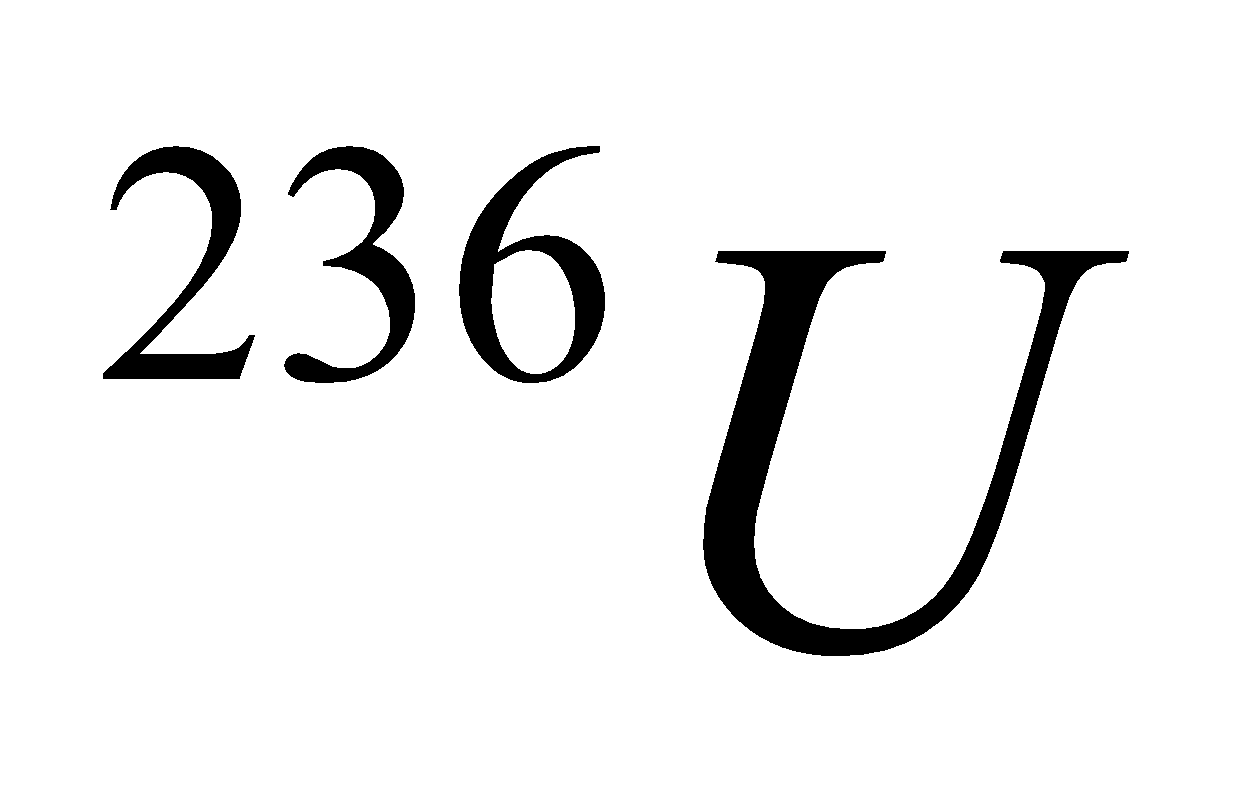
Reproduction factor K 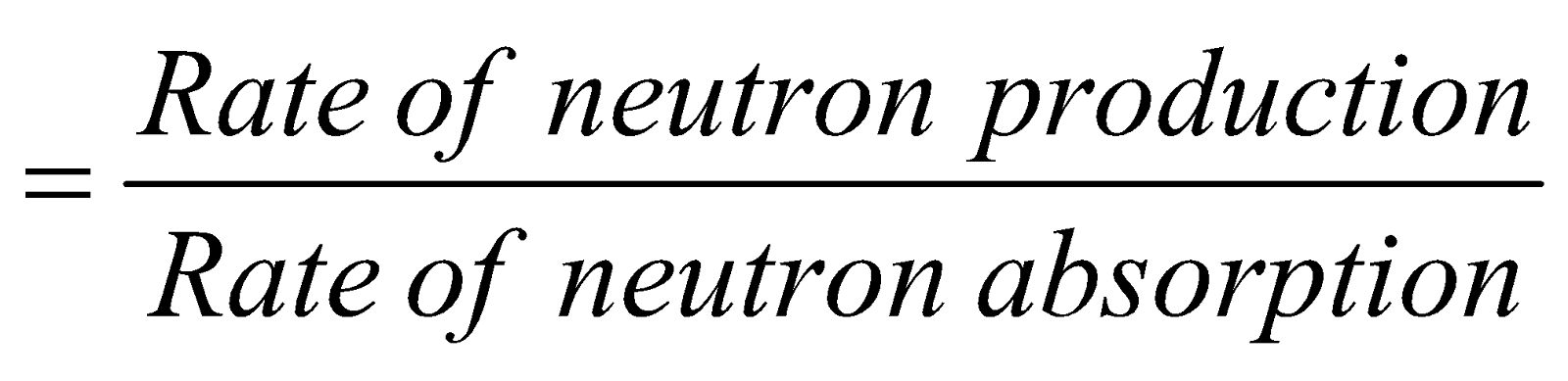
k = 1 for controlled reaction
Breeder reactor :It converts U238 non-fissionable to a fissionable material Pu239 or U235.
NUCLEAR FUSION
Nuclear fusion is the fusion of two or more light nuclei to form a heavy nucleus with a release of huge amount of energy.
For a nuclear fusion to take place, very high temperature is required to overcome the coulombic repulsive forces acting between the nuclei. It is the principle of hydrogen bomb.
The nuclear fusion reaction, which is the source of the energy of sun/ star are proton-proton cycle.
Stars with mass 0.4 to 2.5 solar mass produce energy by carbon-nitrogen cycle. Stars with lower mas produce energy by proton-proton cycle.
NUCLEAR HOLOCAUST
It is the name given to large scale destruction which will be created upon the use of piled up nuclear weapons. It is believed that if the existing nuclear weapons are used, then the radioactive waste will hang like a cloud in the earth’s atmosphere. This cloud will be capable to absorb solar radiation due to which these radiation will not reach earth. This would result to a long nuclear winter.
RADIATION HAZARDS
The γ-radiations are highly energetic and causes pathological and genetic damage.