AP Chemistry: 3.13 Beer-Lambert Law - Exam Style questions with Answer- MCQ

AP PhysicsAP Calculus AP ChemistryAP Biology

Questions

\(Fe^{3+}aq+KSCN_{(s)}\rightarrow FeSCN^{2+}(aq)+K^{+}(aq)\)

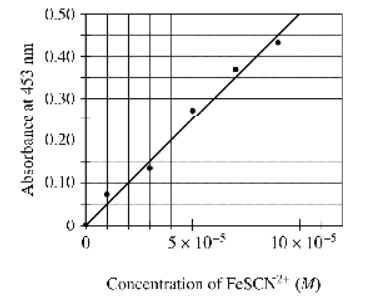
To determine the moles of \(Fe^{3+}(aq)\) in a 100. mL sample of an unknown solution, excess \(KSCN_{s}\) is added to convert all the \(Fe^{3+}(aq)\) into the dark red species \(FeSCN^{2+}(aq)\) , as represented by the equation above. The absorbance of \(FeSCN^{2+}(aq)\) at different concentrations is shown in the graph above. If the absorbance of the mixture is 0.20 at 453 nm, how many moles of \(Fe^{3+}(aq)\) were present in the 100. mL sample? (Assume that any volume change due to adding the \(KSCN_{s}\) is negligible.)
(A) \(4\times10 ^{-4}\) mol
(B) \(3\times10 ^{-4}\) mol
(C) \(4\times10 ^{-4}\) mol
(D) \(3\times10 ^{-4}\) mol

▶️Answer/Explanation

Ans: C

\(\begin{aligned} & A=\varepsilon c l \\ & A=(\varepsilon l) C \\ & y \quad \mathrm{~m} x \\ & \varepsilon l=\text { slope } \\ & \text { Here slope }=\frac{0.29 .0}{5 \times 10^5-0} \\ &=\frac{0.29}{5 \times 10^5} \\ & \text { So, } \\ & \varepsilon l=0.058 \times 10^{-5} \frac{\mathrm{L}}{\mathrm{mol}} \\ & \varepsilon(1 \mathrm{~cm})=0.058 \times 10^{-5} \frac{\mathrm{L}}{\mathrm{mol~\mathrm{cm}}} \end{aligned}\)

\(\begin{aligned} & \text { For Absorbance }=0.20 \\ & \text { Concentration = ?} \\ & A=\varepsilon l c \\ & 0.20=\left(0.058 \times 10^{-5}\right) \cdot \frac{\text { no. of moles }}{\text { volume }} \\ & 0.20=\left(0.058 \times 10^{-5}\right) \cdot \frac{\text { no. of moles }}{100 \mathrm{~mL}} \\ & \frac{0.20 \times 100 \times 10^{-3}}{0.058 \times 10^{-5}}=\text { no. of moles } \\ & \text { no. of moles }=3.5 \times 10^{-4} \mathrm{~mol} \approx 4 \times 10^{-4} \\ & \end{aligned}\)

Question

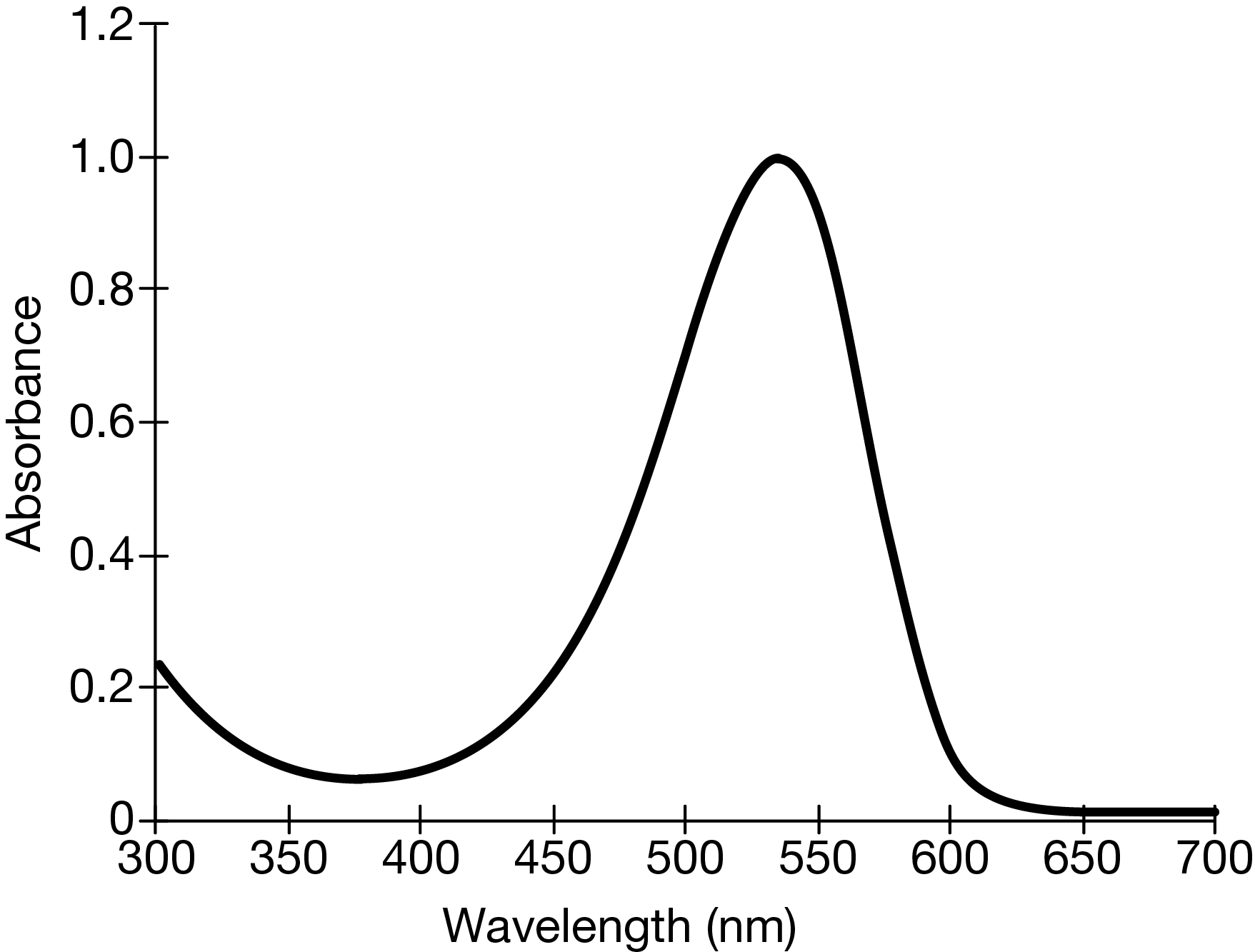
The absorption spectrum of a certain red dye is shown above. If a student analyzing the same concentration of this dye neglected to wipe fingerprints off the cuvette before placing it in the spectrophotometer, how would the absorption curve be affected?

A The peak of the curve would be higher because more light would be absorbed.

B The peak of curve would be lower because less light would be absorbed.

C The peak of the curve would be shifted to the left because less light would be absorbed.

D The peak of the curve would be shifted to the right because more light would be absorbed.

▶️Answer/Explanation

Ans: A

Fingerprints scatter light, so less light would pass through the solution and reach the detector inside the instrument. Less light detected implies more light absorbed. Therefore the peak of the curve would be higher, erroneously indicating that the absorbance is larger than it really is.

Question

A student measures the absorbance of a solution containing \(FeSCN^{2+}\) ions using a spectrophotometer. The cuvette used by the student has two frosted walls and two transparent walls. The student properly orients the cuvette so that the path of the light goes through the transparent sides of the cuvette when calibrating the spectrophotometer. How will the measured absorbance of the \(FeSCN^{2+}\) be affected if the student incorrectly orients the cuvette so that the path of the light is through the frosted sides of the cuvette?

A The measured absorbance of the \(FeSCN^{2+}\) solution will not be affected.

B The measured absorbance of the \(FeSCN^{2+}\) solution will be higher than the actual absorbance.

C The measured absorbance of the \(FeSCN^{2+}\) solution will be lower than the actual absorbance.

D The effect on the measured absorbance of the \(FeSCN_2\) solution depends on the concentration of the \(FeSCN^{2+}\) solution.

▶️Answer/Explanation

Ans: B

The measured absorbance of the \(FeSCN^{2+}\) solution will be higher than the actual absorbance. Some of the light will be scattered/reflected by the frosted surfaces of the cuvette; thus, less light will reach the detector in the spectrophotometer, making it appear as if the sample had absorbed more light.

Question

A student uses a spectrophotometer to analyze a solution of blue food dye. The student first rinses a cuvette with distilled water. Then the student adds the blue dye solution to the cuvette, forgetting to rinse the cuvette with the blue dye solution first. The student places the cuvette in the spectrophotometer and measures the absorbance of the solution. Assuming that some distilled water droplets were still in the cuvette when the blue dye solution was added, how would the measured absorbance be affected?

A The measured absorbance would be too low, because the distilled water left in the cuvette would slightly dilute the solution.

B The measured absorbance would be too low, because the distilled water would change the optimum wavelength of absorbance.

C The measured absorbance would be too high, because the water would allow more light to pass through the cuvette.

D The measured absorbance would be too high, because the distilled water would also absorb some light.

▶️Answer/Explanation

Ans: A

The dilution of the dye solution would lower the concentration of food dye. Less dye in the solution means less absorbance of light; thus the measured absorbance would be too low.