AP Chemistry: 3.4 Ideal Gas Law - Exam Style questions with Answer- MCQ

AP PhysicsAP Calculus AP ChemistryAP Biology

Questions

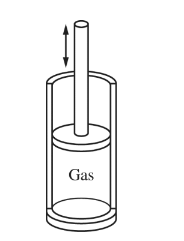
A mixture of two gases, 0.01 mol of$ C_{4}H_{10}$(g) and 0.065 mol of O2(g), is pumped into a cylinder with a movable piston, as shown above. The mixture, originally at $200^{\circ}$ C and 1.0 atm, is sparked and the reaction represented below occurs.
2 $C_{ 4}H_{10}(g) + 13 O_{2}$(g) \rightarrow 8$ CO_{2}(g) + 10 H_{2}$O(g)
Which of the following is true after the product gases return to the original temperature and pressure, and why will the change occur? (Assume all gases behave ideally.)
(A) The piston will be higher than its original position, because the cylinder will contain a greater number of gas molecules.
(B) The position of the piston will be unchanged, because the total mass of the gases in the cylinder does not change.
(C) The position of the piston will be unchanged, because the temperature and pressure of the contents of the cylinder remain the same.
(D) The piston will be lower than its original position, because the product molecules are smaller than the reactant molecules.

▶️Answer/Explanation

Ans: A

Initial mixture: $0.01 \, \text{mol} \, \text{C}_4\text{H}_{10}(g)$ and $0.065 \, \text{mol} \, \text{O}_2(g)$
Initial temperature: $200^\circ \text{C} = 473 \, \text{K}$
Initial pressure: $1.0 \, \text{atm}$
Balanced chemical reaction: $2\text{C}_4\text{H}_{10}(g) + 13\text{O}_2(g) \rightarrow 8\text{CO}_2(g) + 10\text{H}_2\text{O}(g)$

After the reaction, the product gases ($8\text{CO}_2(g) + 10\text{H}_2\text{O}(g)$) return to the original temperature ($473 \, \text{K}$) and pressure ($1.0 \, \text{atm}$).

According to the ideal gas law: $PV = nRT$

Since the temperature and pressure remain constant, the volume occupied by the gases ($V$) will be directly proportional to the total number of moles of gas ($n$).

Let’s calculate the total number of moles before and after the reaction:

Before the reaction:
Total moles $=0.01 |, \text{mol} \, \text{C}_4\text{H}_{10} +0.065|, \text{mol} \, \text{O}_2=0.075 |, \text{mol}$

After the reaction:
Total moles $=8\,\text{mol} \,\text{CO}_2+10 \,\text{mol} \, \text{H}_2\text{O} =18 \, \text{mol}$

Since the total number of moles increases after the reaction ($18 \,\text{mol} >0.075 \,\text{mol}$), the volume occupied by the gases will also increase at constant temperature and pressure.

Therefore, the correct option is (A) The piston will be higher than its original position because the cylinder will contain a greater number of gas molecules.

Question

A 1.0 L sample of a pure gas is found to have a lower pressure than that predicted by the ideal gas law. The best explanation for the observation is that the molecules of the gas

(A) have a combined volume that is too large to be considered negligible when compared to the volume of the container
(B) have a low molecular mass and therefore do not strike the container walls with as much force as expected
(C) are attracted to each other and do not exert as much force on the container walls as they would if they had no mutual attractions
(D) are attracted to the sides of the container and strike the container walls with more force than expected

▶️Answer/Explanation

Ans:C

The deviation from the ideal gas law can occur due to various factors, including the size of gas molecules, intermolecular forces, and the conditions under which the gas is being measured.

Option A suggests that the molecules have a combined volume that is too large to be negligible. In reality, gases are assumed to consist of point-like particles with negligible volume, according to the ideal gas law. When the size of gas molecules becomes significant compared to the volume of the container, the assumption of negligible volume breaks down, and the behavior of the gas deviates from ideal. Therefore, option A could be a valid explanation for the observed deviation from the ideal gas law.

Option B suggests that the low molecular mass of the gas results in fewer collisions with the container walls. However, the ideal gas law doesn’t depend on the molecular mass of the gas; it assumes that gas molecules have mass and move randomly, regardless of their mass.

Option C suggests that the gas molecules are attracted to each other, resulting in fewer collisions with the container walls. This phenomenon is characteristic of real gases, where intermolecular forces affect the behavior of the gas. When gas molecules experience attractive forces, they are less likely to collide with the container walls with the same force as in an ideal gas.

Option D suggests that the gas molecules are attracted to the sides of the container and strike the container walls with more force than expected. This scenario is less likely because attractive forces typically result in fewer collisions with the container walls, leading to lower pressure than expected by the ideal gas law.

Considering the options, option A (the combined volume of gas molecules is not negligible) or option C (the molecules are attracted to each other and do not exert as much force on the container walls) seem more plausible explanations for the observed deviation from the ideal gas law. However, given that real gases often experience both volume effects and intermolecular forces, option C is a more direct explanation for the lower pressure observed. So, the best explanation for the observed deviation is:

(C) The molecules are attracted to each other and do not exert as much force on the container walls as they would if they had no mutual attractions.

Question

A balloon filled with 0.25 mol of He(g) at 273 K and 1 atm is allowed to rise through the atmosphere. Which of the following explains what happens to the volume of the balloon as it rises from ground level to an altitude where the air temperature is 220 K and the air pressure is 0.1 atm?
(A) The volume will increase because the decrease in air pressure will have a greater effect than the decrease in temperature.
(B) The volume will remain unchanged because of the counteracting effects of the decrease in temperature and the decrease in air pressure.
(C) The volume will decrease because the decrease in temperature will have a greater effect than the decrease in air pressure.
(D) It cannot be determined whether the volume of the balloon will increase, decrease, or remain the same without knowing the initial volume of the balloon.

▶️Answer/Explanation

Ans:A

To determine what happens to the volume of the balloon as it rises from ground level to an altitude where the air temperature is 220 K and the air pressure is 0.1 atm, we can apply the ideal gas law equation:

\[ PV = nRT \]

Since the amount of helium gas ($ n $) and the gas constant ($ R $) remain constant, we can rewrite the ideal gas law as:

\[ \frac{P_1}{T_1} = \frac{P_2}{T_2} \]

Where:
$ P_1 $ and $ T_1 $ are the initial pressure and temperature, respectively,
$ P_2 $ and $ T_2 $ are the final pressure and temperature, respectively.

Substituting the given values, we get:

\[ \frac{1 \, \text{atm}}{273 \, \text{K}} = \frac{0.1 \, \text{atm}}{220 \, \text{K}} \]

Solving for the final volume ($ V_2 $), we get:

\[ V_2 = \frac{P_1 \times V_1 \times T_2}{P_2 \times T_1} \]

Given that $ P_1 = 1 \, \text{atm} $, $ T_1 = 273 \, \text{K} $, $ P_2 = 0.1 \, \text{atm} $, and $ T_2 = 220 \, \text{K} $, we can calculate the final volume ($ V_2 $).

When we plug in the values, we get:

\[ V_2 = \frac{1 \times V_1 \times 220}{0.1 \times 273} \]

\[ V_2 = \frac{2200}{27.3} \times V_1 \]

\[ V_2 \approx 80.52 \times V_1 \]

This means the final volume ($ V_2 $) will be approximately $80.52$ times the initial volume ($ V_1 $). Since $80.52$ is much greater than $1$, it indicates that the volume of the balloon will increase significantly as it rises to the altitude with lower temperature and pressure.

Therefore, the correct answer is:

(A) The volume will increase because the decrease in air pressure will have a greater effect than the decrease in temperature.

Questions

The ideal gas law best describes the properties of which of the following gases at $^{\circ }C$ and 1 atm?
(A) $PH_{3}$
(B) $HBr$
(C) $SO_{2}$
(D) $N_{2}$

▶️Answer/Explanation

Ans: D

The ideal gas law, $PV = nRT$, where $P$ is pressure, $V$ is volume, $n$ is the number of moles, $R$ is the ideal gas constant, and $T$ is temperature in Kelvin, best describes gases under conditions where the gas particles are far apart and there are no intermolecular forces between them.

At $^{\circ }C$ and 1 atm, gases behave most ideally when they are at high temperatures and low pressures. This means that they are less likely to deviate from ideal gas behavior.

Among the options provided, nitrogen ($N_{2}$) is most likely to behave like an ideal gas at $^{\circ }C$ and 1 atm, as it consists of diatomic molecules and has weak intermolecular forces. So, the correct answer is (D) $N_{2}$.

Questions

When 4.0 L of $He_{g}$, 6.0 L of $N_{2(g)}$), and 10. L of $Ar_{(g)}$, all at 0°C and 1.0 atm, are pumped into an evacuated 8.0 L rigid container, the final pressure in the container at $0^{\circ }C$ is
(A) 0.5 atm
(B) 1.0 atm
(C) 2.5 atm
(D) 4.0 atm

▶️Answer/Explanation

Ans: C

To solve this problem, we need to use the ideal gas law: $ PV = nRT $, where $ P $ is the pressure, $ V $ is the volume, $ n $ is the number of moles, $ R $ is the universal gas constant, and $ T $ is the absolute temperature.

Given information:
Volume of $ \text{He(g)} $ = 4.0 L
Volume of $ \text{N}_2(\text{g}) $ = 6.0 L
Volume of $ \text{Ar(g)} $ = 10.0 L
Temperature = 0°C = 273.15 K
Pressure = 1.0 atm
Final volume of the container = 8.0 L

Calculate the number of moles of each gas using the ideal gas law.

\[ n = \frac{PV}{RT} \]
\[ R = 0.08206 \, \text{L atm mol}^{1} \text{ K}^{1} \]

For $ \text{He(g)} $:
\[ n(\text{He}) = \frac{(1.0 \, \text{atm} \times 4.0 \, \text{L})}{(0.08206 \, \text{L atm mol}^{1} \text{ K}^{1} \times 273.15 \, \text{K})} = 0.178 \, \text{mol} \]

For $ \text{N}_2(\text{g}) $:
\[ n(\text{N}_2) = \frac{(1.0 \, \text{atm} \times 6.0 \, \text{L})}{(0.08206 \, \text{L atm mol}^{1} \text{ K}^{1} \times 273.15 \, \text{K})} = 0.267 \, \text{mol} \]

For $ \text{Ar(g)} $:
\[ n(\text{Ar}) = \frac{(1.0 \, \text{atm} \times 10.0 \, \text{L})}{(0.08206 \, \text{L atm mol}^{1} \text{ K}^{1} \times 273.15 \, \text{K})} = 0.445 \, \text{mol} \]

Calculate the total number of moles in the final container.

\[ n(\text{total}) = n(\text{He}) + n(\text{N}_2) + n(\text{Ar}) \]
\[ n(\text{total}) = 0.178 \, \text{mol} + 0.267 \, \text{mol} + 0.445 \, \text{mol} = 0.890 \, \text{mol} \]

Calculate the final pressure in the container using the ideal gas law.

\[ P = \frac{n(\text{total}) \times RT}{V} \]
\[ P = \frac{0.890 \, \text{mol} \times 0.08206 \, \text{L atm mol}^{1} \text{ K}^{1} \times 273.15 \, \text{K}}{8.0 \, \text{L}} \]
\[ P = 2.5 \, \text{atm} \]

Therefore, the correct answer is (C) 2.5 atm.

Question

A gaseous air‑fuel mixture in a sealed car engine cylinder has an initial volume of $600. milliliters$ at $1.0 atmosphere$ . To prepare for ignition of the fuel, a piston moves within the cylinder, reducing the volume of the air‑fuel mixture to $50. milliliters$ at constant temperature. Assuming ideal behavior, what is the new pressure of the air‑fuel mixture?

A About

0.083 atmosphere

, because the initial volume of the gas mixture was 12 times larger than its final volume.

B About

12 atmospheres

, because the volume of the gas mixture decreased by a factor of 12.

C About

120. atmospheres

, because the initial volume of the gas mixture was 120 times larger than its final volume.

D About

550. atmospheres

, because the change in the volume of the gas mixture was

550. milliliters

▶️Answer/Explanation

Ans:B

For a gas or gas mixture that behaves ideally, pressure and volume are inversely proportional. Therefore, since $n$ and $T$ remained constant, a 12-fold decrease in volume should result in a 12-fold increase in pressure.

Question

At $10. degrees Celsius$ , $20. grams$ of oxygen gas exerts a pressure of $2.1 atmospheres$ in a rigid, $7.0 Liter$ cylinder. Assuming ideal behavior, if the temperature of the gas was raised to $40. degrees Celsius$ , which statement indicates the new pressure and explains why?

1.9 atmospheres

, because the pressure

P

decreases by the proportion $\frac{283}{313}$

2.3 atmospheres

, because the pressure

P

increases by the proportion $\frac{313}{283}$

0.52 atmosphere

, because the pressure

P

decreases by the proportion $\frac{10}{40}$

10 over 40

8.4 atmospheres

, because the pressure

P

increases by the proportion $\frac{40}{10}$

▶️Answer/Explanation

Ans: B

Rearranging the ideal gas law equation yields the equation $P=\frac{nRT}{V}$

Since the number of moles of oxygen $(n)$ , the gas constant $(R)$ , and the volume $(V)$ are all constant in this case, the relationship reduces to $P = k T$ , where $T$ is the absolute temperature (in kelvins). Therefore, increasing the temperature to 313 $K$ from 283 $K$ results in a pressure that is larger by the factor $\frac{313}{283}$

Question

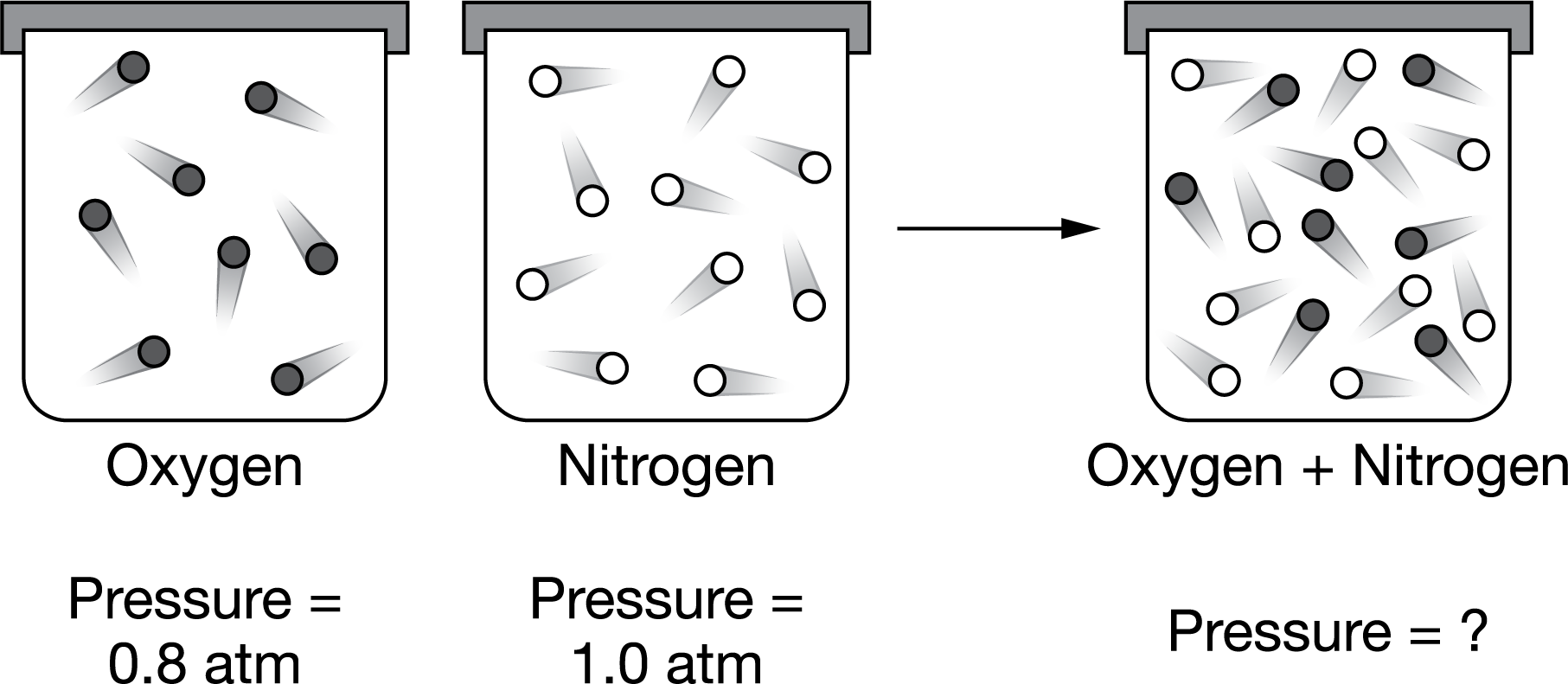
Two sealed, rigid $5.0 Liters$ containers each contain a gas at the same temperature but at a different pressure, as shown above. Also shown are the results of transferring the entire contents of container 1 to container 2. No gases escape during the transfer. Assuming ideal behavior, which statement is correct regarding the total pressure of the gases after they are combined?

A The total pressure of the gases in the mixture is the sum of the initial pressures of oxygen gas and nitrogen gas because pressure only depends on the total amount of gas when volume and temperature are held constant.

B The total pressure of the gases in the mixture is lower than the sum of the initial pressures of oxygen and nitrogen because some of the energy of the particles will be lost due to an increase in the number of collisions.

C The total pressure of the gases in the mixture is higher than the sum of the initial pressures of oxygen and nitrogen because of the intermolecular forces that develop between oxygen and nitrogen molecules.

D The total pressure of the gases in the mixture cannot be determined because the actual value of the temperature is not given.

▶️Answer/Explanation

Ans: A

Under conditions of constant $T$ and $V$ , the pressure of a gas or a mixture of gases only depends on the total number of moles of gas, regardless of the identity of the gas. From the ideal gas law, thus $P$ is directly proportional to $n$ , since $R$ , $T$ , and $V$ are constant. Since the total amount of gas in the mixture is the sum of the original amounts of each gas, meaning that the total pressure of the gas mixture is simply the sum of the initial pressures of each gas.

Question

Under which of the following conditions of temperature and pressure will $H_2$ gas be expected to behave most like an ideal gas’?

(A)50 K and 0.10 atm

(B)50 K and 5.0 atm

(D) 500 K and 50 atm

▶️Answer/Explanation

Ans:C