AP Chemistry: 3.5 Kinetic Molecular Theory - Exam Style questions with Answer- MCQ

AP PhysicsAP Calculus AP ChemistryAP Biology

Questions

As a sample of $KNO_3$(s) is stirred into water at 25°C, the compound dissolves endothermically. Which of the following best helps to explain why the process is thermodynamically favorable at 25°C?
(A) All endothermic processes are thermodynamically favorable.
(B) Stirring the solution during dissolution adds the energy needed to drive an endothermic process.
(C) Dissolving the salt decreases the enthalpy of the system.
(D) Dissolving the salt increases the entropy of the system.

▶️Answer/Explanation

>Ans: D

The correct answer is (D) Dissolving the salt increases the entropy of the system.

For a process to be thermodynamically favorable at a given temperature, the total entropy change (AStotal) must be positive. The total entropy change is the sum of the entropy change due to the process itself
(ASsystem) and the entropy change due to the transfer of heat between the system and the surroundings (ASsurroundings).

In the case of the endothermic dissolution of KNO3(s) in water at 25C, the following considerations apply:

(A) All endothermic processes are thermodynamically favorable: This statement is incorrect. Both exothermic and endothermic processes can be thermodynamically favorable or unfavorable, depending on the
entropy change.

(B) Stirring the solution during dissolution adds the energy needed to drive an endothermic process: This statement is incorrect. Stirring may facilitate the dissolution process by increasing the rate of mixing,
but it does not provide the energy required for the endothermic process.

(C) Dissolving the salt decreases the enthalpy of the system: This statement is incorrect for an endothermic process. Endothermic processes involve an increase in the enthalpy of the system.

(D) Dissolving the salt increases the entropy of the system: This statement is correct. When a solid salt dissolves in water, the ions become more disordered and dispersed, resulting in an increase in entropy
(ASsystem > o). Additionally, the absorption of heat from the surroundings during the endothermic process also contributes to an increase in the entropy of the surroundings (ASsurroundings >0).

The increase in total entropy (AStotal = ASsystem + ASsurroundings) is what makes the endothermic dissolution process thermodynamically favorable at 25C, despite the increase in enthalpy.

Questions

A sealed 10.0 L flask at 400 K contains equimolar amounts of ethane and propanol in gaseous form.
Which of the following statements concerning the average molecular speed of ethane and propanol is true?
(A) The average molecular speed of ethane is less than the average molecular speed of propanol.
(B) The average molecular speed of ethane is greater than the average molecular speed of propanol.
(C) The average molecular speed of ethane is equal to the average molecular speed of propanol.
(D) The average molecular speeds of ethane and propanol cannot be compared without knowing the total pressure of the gas mixture.

▶️Answer/Explanation

Ans: A

To compare the average molecular speeds of ethane and propanol, we can use the formula for the average molecular speed, which is given by:

\[ \text{Average molecular speed} = \sqrt{\frac{3RT}{M}} \]

where:

$ R $ is the gas constant,
$ T $ is the temperature in Kelvin,
$ M $ is the molar mass of the gas.

Since both ethane and propanol are in gaseous form, they behave ideally, and we can use this formula.

Given that the temperature ($ T $) is the same for both gases and that they contain equimolar amounts, we only need to compare their molar masses ($ M $).

The molar mass of ethane is approximately 30 g/mol, and the molar mass of propanol is approximately 60 g/mol.

Since the molar mass of propanol is greater than that of ethane, propanol molecules have a greater mass compared to ethane molecules. According to the formula for average molecular speed, a greater molar mass results in a lower average molecular speed.

So, the correct answer is:

(A) The average molecular speed of ethane is less than the average molecular speed of propanol.

Question

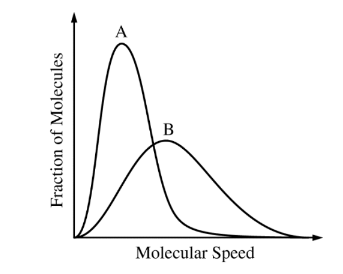
The Maxwell-Boltzmann distributions of molecular speeds in samples of two different gases at the same temperature are shown above. Which gas has the greater molar mass?
(A) Gas A
(B) Gas B
(C) Both gases have the same molar mass.
(D) It cannot be determined unless the pressure of each sample is known.

Answer/Explanation

Ans:A

The Maxwell-Boltzmann distribution curve of molecular speeds is inversely proportional to the molar mass of the gas. Therefore, the gas with the slower distribution curve, which is shifted more towards the left side of the graph, has the greater molar mass. In the given graph, Gas A has the slower distribution curve, indicating that it has the greater molar mass compared to Gas B.

Question

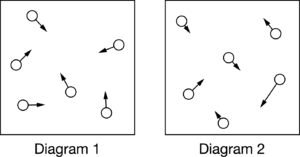
The diagrams above use arrows to represent the speed of a gas particle. Which of the diagrams best represents the speed of the particles of a gas at a fixed temperature, and why?

A Diagram 1, because all the particles have the same speed.

B Diagram 1, because the particles are moving in different directions.

C Diagram 2, because the particles have a net kinetic energy of zero.

D Diagram 2, because the particles have a variety of different speeds.

▶️Answer/Explanation

Ans: D

Based on kinetic molecular theory, gas particles have a distribution of speeds that is dependent on the temperature, which is represented in diagram 2.

Question

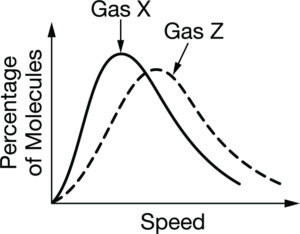
The two gas samples represented in the graph above are at the same temperature. Which of the following statements about the gases is correct?

A The molecules of gas $Z$ have a higher average kinetic energy than the molecules of gas $X$ .

B There are fewer molecules in the sample of gas $Z$ than in the sample of gas $X$ .

C Gas $Z$ has a smaller molar mass than gas $X$ .

D Gas

Z

has a greater molar mass than gas

X

▶️Answer/Explanation

Ans:C

Gases at the same temperature have the same average kinetic energy of their molecules. Since KE $=\frac{1}{2}m_Xv_Y^2=\frac{1}{2}m_Zv_Z^2$ $K E = \frac{1}{2} m_{X} v_{X}^{2} = \frac{1}{2} m_{Z} v_{Z}^{2}$ , the gas with the higher average molecular speed has the lower molar mass $m_X/v_Z=v_Z^2/v_X^2$ . The curve for gas $Z$ shows that the molecules have a higher average speed than the molecules in gas $X$ , so gas $Z$ has a smaller molar mass.

Question

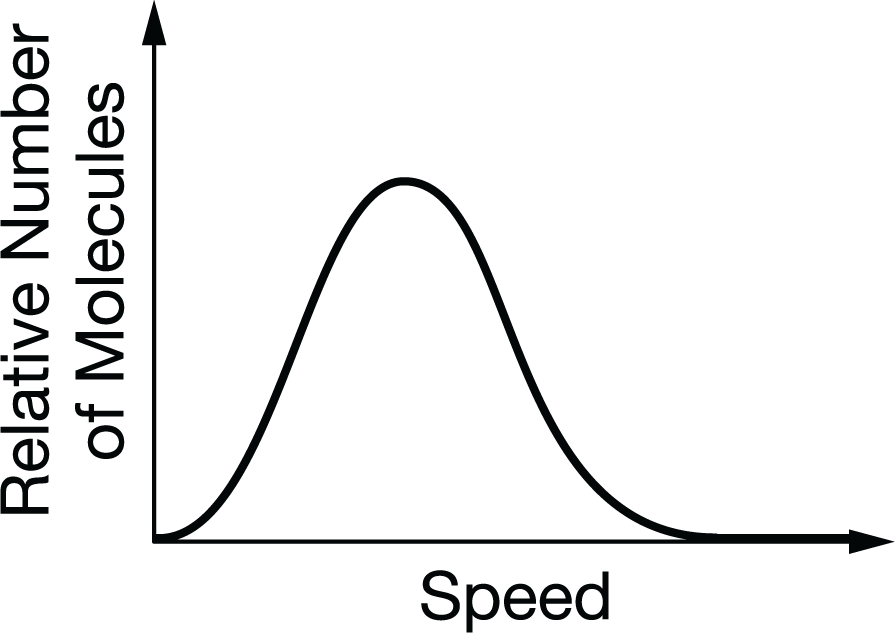
The diagram above shows the distribution of speeds for a sample of $O 2, gaseous$ . Which of the following graphs shows the distribution of speeds for the same sample at a higher temperature (dashed line) ?

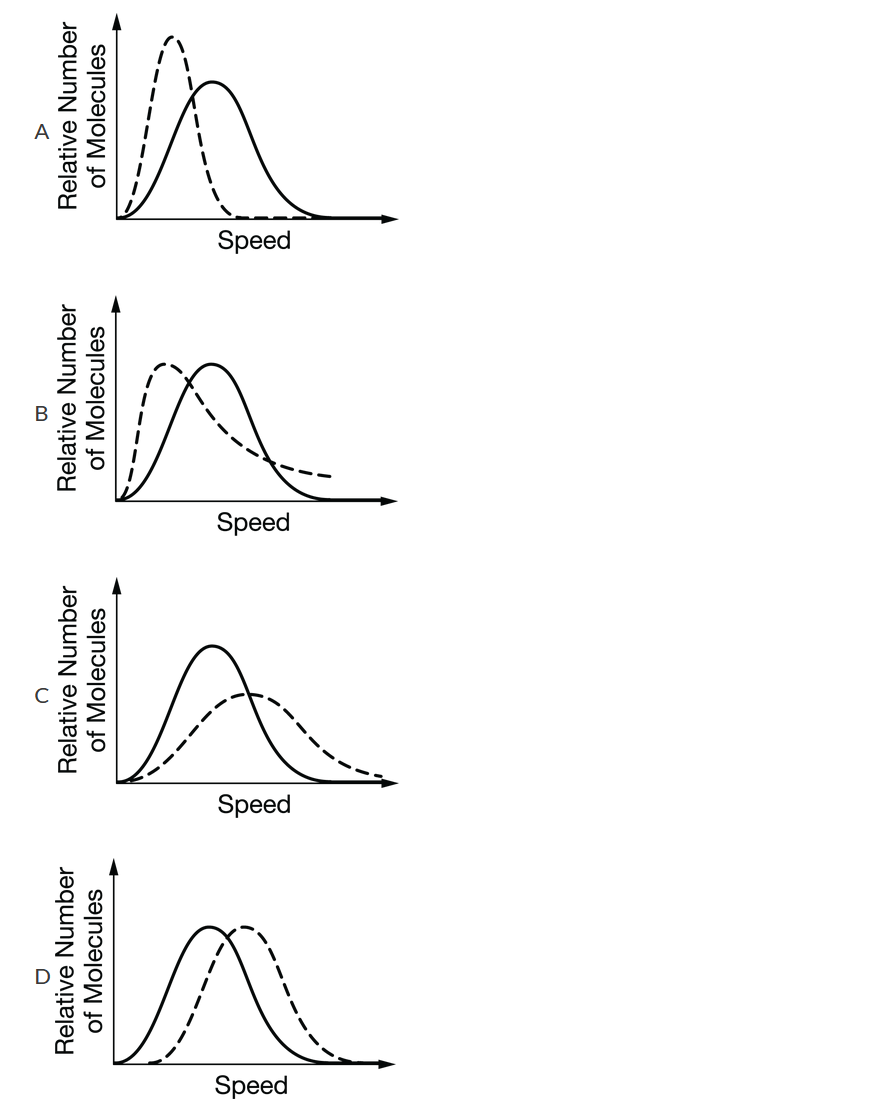
▶️Answer/Explanation

Ans: C

When the temperature increases, the average speed of the gas molecules increases. The peak is to the right of the original peak, and the relative number of molecules at the highest speeds is greater.

Question

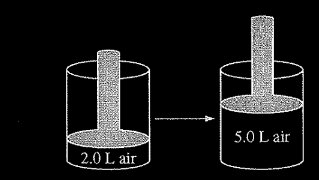
The volume of a sample of air in a cylinder with a movable piston is 2.0 L at a pressure $P_1$ , as shown in the diagram above. The volume is increased to 5.0 L as the temperature is held constant. The pressure of the air in the cylinder is now $P_2$. What effect do the volume and pressure changes have on the average kinetic energy of the molecules in the sample?

(A)The average kinetic energy increases.

(B)The average kinetic energy decreases.

(C)The average kinetic energy stays the same.

(D) It cannot be determined how the kinetic energy is affected without knowing

▶️Answer/Explanation

Ans:C

Refer to the foll0wing.

The table below contains information about particles is samples of four different gases at 273 K. The (A) greatest in container I samples are in four identical rigid containers (B) greatest in container 2 numbered 1 through 4.

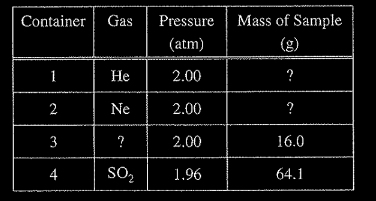
Question

Under the conditions given, consider containers 1, 2, and 4 only. The average speed of the gas particles is

(A) greatest in container 1

(B) greatest in container 2

(D) the same in containers 1, 2, and 4

▶️Answer/Explanation

Ans:A