Questions
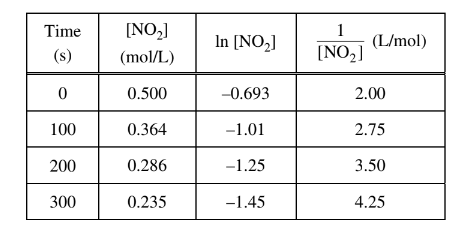
The data from a study of the decomposition of \(NO_2\)(g) to form NO(g) and \(O_2\)(g) are given in the table above. Which of the following rate laws is consistent with the data?
(A) Rate = \(k[NO_{2}]\)
(B) Rate=\(k[NO_{2}]^{2}\)
(C) Rate=\(K\frac{1}{[NO_{2}]}\)
(D) Rate= \(K\frac{1}{[NO_{2}]^{2}}\)
▶️Answer/Explanation
Ans: A
To determine the rate law from the given data, we can utilize the integrated rate laws for first-order and second-order reactions.
For a first-order reaction, the integrated rate law is:
\[ \ln{[\text{NO}_2]} = -kt + \ln{[\text{NO}_2]_0} \]
For a second-order reaction, the integrated rate law is:
\[ \frac{1}{[\text{NO}_2]} = kt + \frac{1}{[\text{NO}_2]_0} \]
Comparing the given data with the integrated rate laws, we can identify the order of the reaction.
Looking at the data, when the concentration of \(NO_2\) decreases, the natural logarithm of \(NO_2\) increases linearly with time. This behavior is consistent with a first-order reaction.
Therefore, the rate law for a first-order reaction is:
\[ \text{Rate} = k[\text{NO}_2]\]
So, the correct answer is: (A) Rate =\(k[NO_{2}]\)
Question
\(2NOBr(g)\rightarrow 2NO(g)+Br_{2}(g)\)
The equation above represents an elementary step in a chemical reaction. Which of the following is the correct expression for the rate law of the elementary step?
(A) Rate=k[NOBr]^{\frac{1}{2}}
(B) Rate=k[NOBr]
(C) Rate= \(k[NOBr]^{2}\)
(D) Rate= \(k[NO]^{2}[Br_{2}]\)
▶️Answer/Explanation
Ans:C
The given equation is:
\[ 2NOBr(g) \rightarrow 2NO(g) + Br_2(g) \]
From the balanced equation, we can see that the reactant is \(NOBr\). The stoichiometric coefficient of \(NOBr\) in the balanced equation is 1. Therefore, the rate law expression will depend on the concentration of \(NOBr\).
However, this is a bimolecular reaction, meaning two molecules of \(NOBr\) are involved in the rate-determining step. Therefore, the rate law expression will include \(NOBr\) raised to the power of 2.
So, the correct expression for the rate law of the elementary step is:
(C) Rate = \(k[NOBr]^2\)
Questions
\(N_{2}O_{4(g)}\rightleftharpoons 2NO_{2(g)}\) \(K_{p}=3.0 at 70^{\circ C}\)
colorless brown
A mixture of \(NO_{2(g)}\) and \(N_{2}O_{4(g)}\) is placed in a glass tube and allowed to reach equilibrium at \(70^{\circ C}\), as represented above. If \(P_{N_{2}O_{4}}\) is 1.33 atm when the system is at equilibrium at 70 \(70^{\circ C}\) , what is \(P_{NO_{2}}\)?
(A) 0.44 atm
(B) 2.0 atm
(C) 2.3 atm
(D) 4.0 atm
▶️Answer/Explanation
Ans: B
\[
\mathrm{N}_2 \mathrm{O}_4(\mathrm{~g}) ; 2 \mathrm{NO}_2(9)
\]
At Equilibrium the relation between partial pressure and \(\mathrm{kp}\) is
\[
\begin{gathered}
k_p=\frac{\left(P\left[\mathrm{NO}_2\right]\right)^2}{P\left[\mathrm{~N}_2 \mathrm{O}_4\right]} \\
k_P=3.0& P\left[\mathrm{~N}_2 \mathrm{O}_4\right]=1.33 \mathrm{~atm}
\end{gathered}
\]
Put the values of \(\mathrm{Kp}\) and \(P\left[\mathrm{~N}_2 \mathrm{O}_4\right]\) in above \(\varepsilon_{2 n}\)
\[
\begin{aligned}
3 & =\frac{\left(P\left[\mathrm{NO}_2\right]\right)^2}{1.33} \\
3.99 & =\left(P\left[\mathrm{NO}_2\right]\right)^2 \\
P\left[\mathrm{NO}_2\right] & =1.99749 \text { atm } \\
P\left[\mathrm{NO}_2\right] & \approx 2 \mathrm{~atm} \quad \text { (Approximate) }
\end{aligned}
\]
Question
\(2X+Y_2→X_2Y_2\)
A chemist is studying the reaction between the gaseous chemical species X and \(Y_2\), represented by the equation above. Initial rates of reaction are measured at various concentrations of reactants. The results are recorded in the following table.
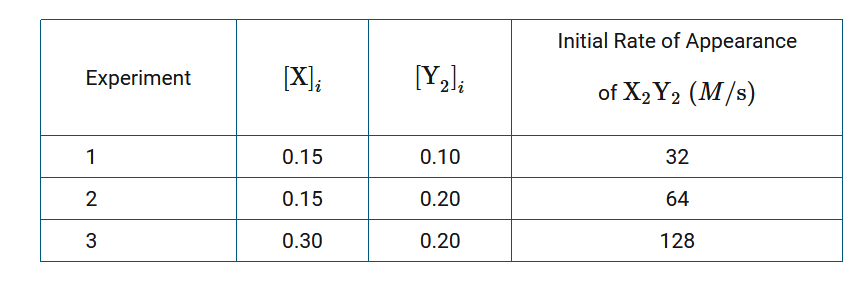
Given the information in the table above, which of the following is the experimental rate law?
A Rate=\(k[X][Y_2]\)
B Rate=\(k[X]^2[Y_2]\)
C Rate=\(k[X][Y_2]^2\)
D Rate=\(k[X]^2[Y_2]^2\)
▶️Answer/Explanation
Ans: A
Comparing experiment 1 with experiment 2, a doubling of \([Y_2]_i\) while keeping \([X]_i\) constant resulted in a doubling of the reaction rate. Thus, the reaction is first order with respect to \(Y_2\). A similar comparison of experiment 2 with experiment 3 reveals that the reaction is first order with respect to X. Thus, the exponent of the concentrations of reactants in the rate law are both equal to 1.
Question
\(2X+Y_2→X_2Y_2\)
A chemist is studying the reaction between the gaseous chemical species X and \(Y_2\), represented by the equation above. Initial rates of reaction are measured at various concentrations of reactants. The results are recorded in the following table.

Given the information in the table above, which of the following is the experimental rate law?
A Rate=\(k[X][Y_2]\)
B Rate=\(k[X]^2[Y_2]\)
C Rate=\(k[X][Y_2]^2\)
D Rate=\(k[X]^2[Y_2]^2\)
▶️Answer/Explanation
Ans: A
Comparing experiment 1 with experiment 2, a doubling of \([Y_2]_i\) while keeping \([X]_i\) constant resulted in a doubling of the reaction rate. Thus, the reaction is first order with respect to \(Y_2\). A similar comparison of experiment 2 with experiment 3 reveals that the reaction is first order with respect to X. Thus, the exponent of the concentrations of reactants in the rate law are both equal to 1.
Question
\(2X+Y_2→X_2Y_2\)
A chemist is studying the reaction between the gaseous chemical species X and \(Y_2\), represented by the equation above. Initial rates of reaction are measured at various concentrations of reactants. The results are recorded in the following table.

Based on the information above, determine the initial rate of disappearance of X in experiment 1.
A 16M/s
B 32M/s
C 64M/s
D 128M/s
▶️Answer/Explanation
Ans: C
The initial rate of disappearance of X is equal to twice the initial rate of appearance of X2Y2 and given by the following:
\((\frac{\Delta [X]}{\Delta t})=-2\times(\frac{\Delta[X2Y2]}{\Delta t})\)=2×(initial rate of reaction)=2×32M/s=64M/s.
The negative sign indicates that the concentration of X is decreasing
Question
\(CH_3I+NaOH→CH_3OH+NaI\)
The rate of the reaction represented by the chemical equation shown above is expressed as rate \(=k[CH_3I][NaOH]\) . Based on this information, which of the following claims is correct?
A The reaction will proceed at a slower rate with increasing temperature.
B The rate of the reaction will double when the concentrations of both \(CH_3I\) and NaOH are doubled.
C The rate of the reaction will double if the concentration of \(CH_3I\) is doubled while keeping the concentration of NaOH constant.
D A larger amount of \(CH_3OH\) will be produced if the concentrations of \(CH_3I\) and NaOH are halved.
▶️Answer/Explanation
Ans: C
Based on the information given, doubling the concentration of \(CH_3I\) while keeping the concentration of NaOH constant will double the rate of the reaction. Based on collision theory, the rate is faster as a result of the increased frequency of collisions when the concentration is increased.
Question.
\(NO_{2}(g) + CO(g) → NO(g) + CO_{2}\)(g)
The reaction between \(NO_{2}\)(g) and CO(g) is represented above. The elementary steps of a proposed reaction mechanism are represented below. Step 1: 2 \(NO_{2}(g) → NO(g) + NO_{3}(g) \)Step 2: \(NO_{3}(g) + CO(g) → NO_{2}(g) + CO_{2}(g) \)(slow) (fast) Which of the following is the rate law for the overall reaction that is consistent with the proposed mechanism?
(A) Rate = k\( [NO_{2}][CO]\)
(B) Rate = k\( [NO_{2}]^{2}\)
(C) Rate = k\( [NO_{3}][CO]\)
(D) Rate = k\( [NO_{2}][NO][CO]\)
▶️Answer/Explanation
Ans:B
Question

The data from a study of the decomposition of \(NO_2\)(g) to form NO(g) and \(O_2\)(g) are given in the table above. Which of the following rate laws is consistent with the data?
(A) Rate = \(k[NO_{2}]\)
(B) Rate=\(k[NO_{2}]^{2}\)
(C) Rate=\(K\frac{1}{[NO_{2}]}\)
(D) Rate= \(K\frac{1}{[NO_{2}]^{2}}\)
▶️Answer/Explanation
Ans:B