Question
\(2N_2O_5(g)→4NO_2(g)+O_2(g)\)
For the reaction represented by the equation above, the concentration of \(N_2O_5\) was measured over time. The following graphs were created using the data.
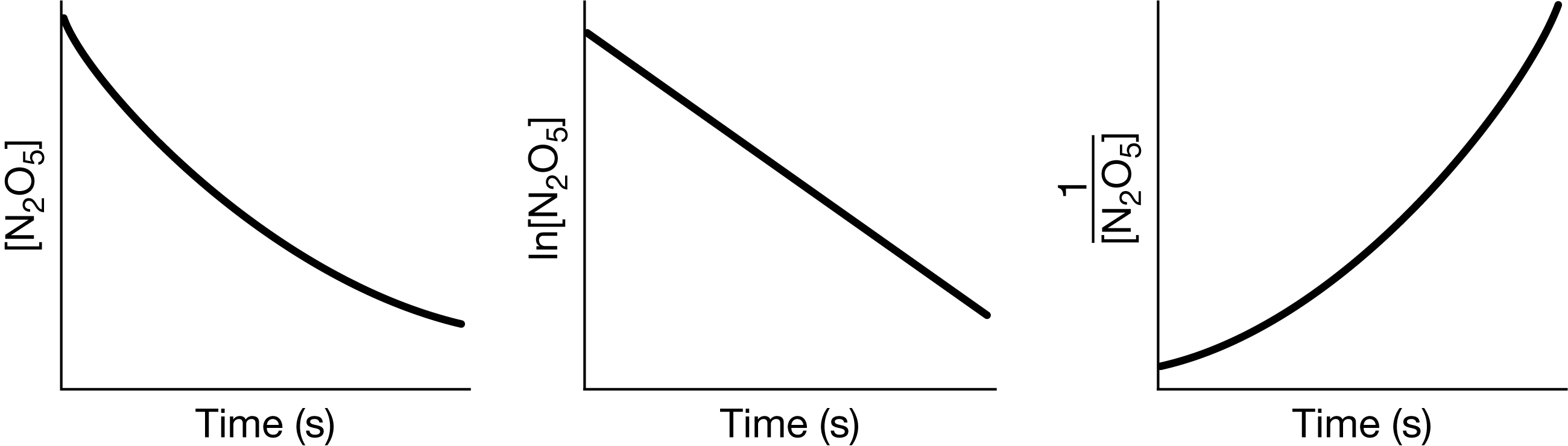
For the reaction represented by the equation above, the concentration of \(N_2O_5\) was measured over time. The following graphs were created using the data. Based on the graphs above, what is the order of the reaction with respect to \(N_2O_5\)?
A Zeroth order
B First order
C Second order
D Third order
▶️Answer/Explanation
Ans:B
For a first-order reaction, graphing \(ln[N_2O_5]\) versus time produces a straight line.
Question
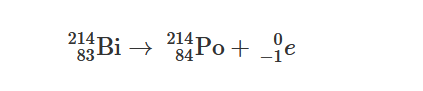
Bismuth-214 undergoes first-order radioactive decay to polonium-214 by the release of a beta particle, as represented by the nuclear equation above. Which of the following quantities plotted versus time will produce a straight line? (n = the number of moles in the sample)
A \(n_{Bi}\)
B \(n_{Po}\)
C \(ln(n_{Bi})\)
D \(\frac{1}{n_{Bi}}\)
▶️Answer/Explanation
Ans:C
Because the reaction is a first-order radioactive decay, a plot of \(n_{Bi}\) versus time would produce a straight line.
Question
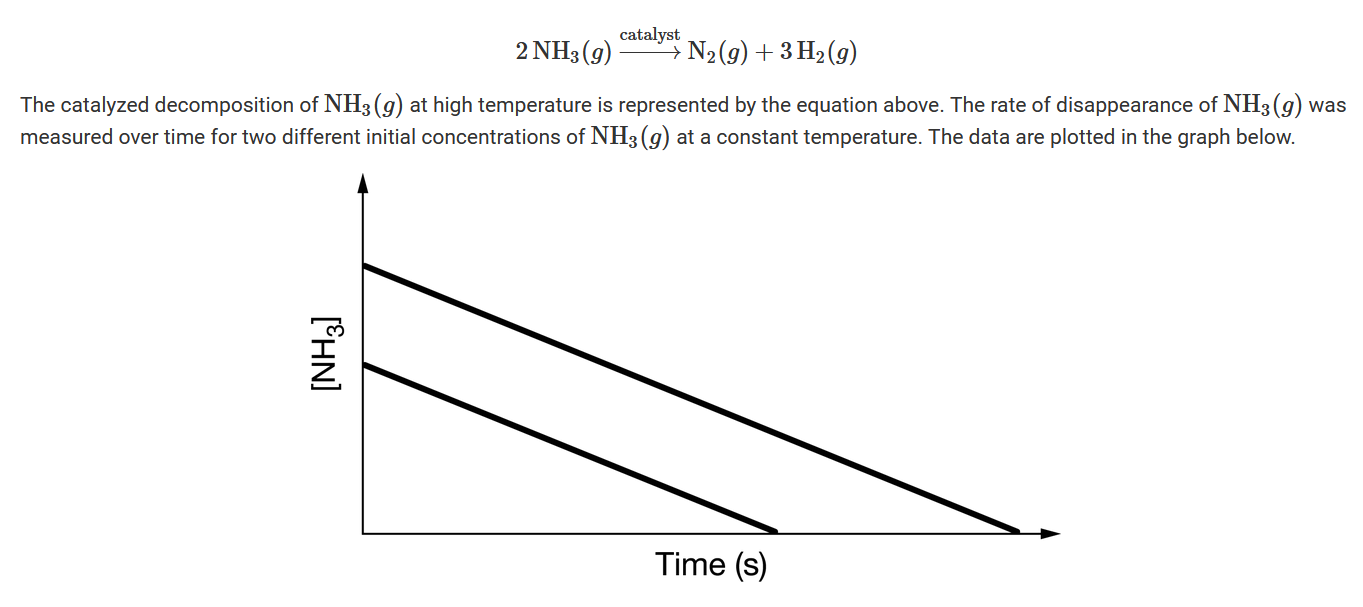
On the basis of the data in the graph, which of the following best represents the rate law for the catalyzed decomposition of \(NH_3\)(g)?
A Rate\(=k\)
B Rate\(=k[NH_3]\)
C Rate\(=k[NH_3]^2\)
D Rate\(=k[N_2][H_2]\)
▶️Answer/Explanation
Ans:A
The plots of \([NH_3]\) versus time for the two different initial concentrations of ammonia are straight lines with identical slopes. The slope is equal to \(\frac{\Delta[NH3]}{\Delta t}\), which is constant and equal to the rate of reaction. In other words, the rate is independent of \([NH_3]\), and the reaction is zeroth order with rate=k.
Refer to the following.
\(5 H_2O_2(aq) + 2 MnO_{4} ̄(aq) + 6 H^{+}(aq) \rightarrow 2 Mn^{2+}(aq) + 8 H_{2}O(l) + 5 O_{2}(g)\)
In a titration experiment,\( H_{2}O_{2}(aq)\) reacts with aqueous\( MnO_4^{+}(aq) \)as represented by the equation above. The dark purple \(KMnO_{4}\) solution is added from a buret to a colorless, acidified solution of\( H_{2}O_{2}\)(aq) in an Erlenmeyer flask. (Note: At the end point of the titration, the solution is a pale pink color.)
Question
At a certain time during the titration, the rate of appearance of \(O_2\)(g) was \(1.0 × 10^{-3}\) mol/(L·s). What was the rate of disappearance of \(MnO_4^{-}\) at the same time?
(A) 6.0 ×\( 10^{-3}\) mol/(L.s)
(B) 4.0 ×\( 10^{-3}\) mol/(L.s)
(C)\( 6.0 × 10^{-4}\) mol/(L.s)
(D) 4.0 x 10 mol/(L.s)
▶️Answer/Explanation
Ans:D