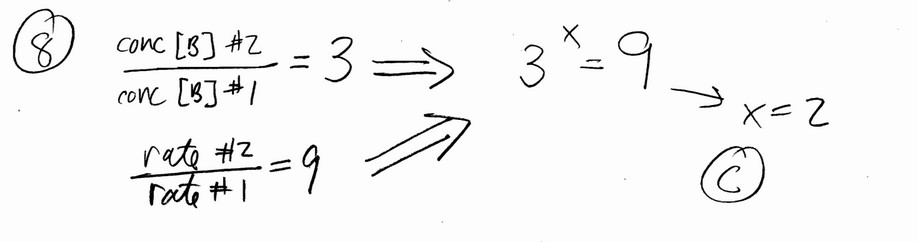Question
X → Products
A student studied the kinetics of the reaction represented above by measuring the concentration of the reactant, X, over time. The data are plotted in the graph below.

Which of the following procedures will allow the student to determine the rate constant, k, for the reaction?
(A) Plot ln [X] versus time and determine the magnitude of the slope.
(B) Plot \(\frac{1}{[X]}\) versus time and determine the magnitude of the slope.
(C) Run another trial of the experiment with a different initial concentration, plot the data on the same graph, and see where the curves intersect.
(D) Run another trial of the experiment at a different temperature, plot the data on the same graph, and see where the curves have the same slope.
▶️Answer/Explanation
Ans:A
If you look closely, you can see that, after every 20 minutes, the concentration is halved.
t [x] (m)
0 1.0
20 0.5
40 0.25
60 0.125
Half life of the reaction is 20 min. It is a first order reaction. For a first order reaction: ln [X] = ln [X]o – kt ln[X] vs time graph is a straight line which has a slope of -k. Rate constant (k) = magnitude of ln[X]-vs slope of ln[X] vs time graph.
To determine the rate constant k, for the reaction, (A) Plot plot ln [X] versus time and determine the magnitude of the slope.
Questions

Based on the information above, which of the following expressions represents the equilibrium constant, K, for the reaction represented by the equation below?
\(La^{3+}+CO_{3}^{2}\leftrightharpoons LaCO_{3}^{+}\)
(A) K=\((K_{1}),(K_{a}),(K_{w})\)
(B) K= \(\frac{(K_{1})(K_{a})}{(K_{w})}\)
(C) K=\(\frac{(K_{1} }{(K_{a})(K_{w}))}\)
(D) K =\(\frac{(K_{1})(K_{w})}{(K_{a})}\)
▶️Answer/Explanation
Ans: D
Given:
1. \( \text{La}^{3+} + \text{OH}^- + \text{HCO}_3^- \rightleftharpoons \text{LaCO}_3^+ + \text{H}_2\text{O} \) ( \( K_1 \) )
2. \( \text{HCO}_3^- \rightleftharpoons \text{H}^+ + \text{CO}_3^{2-} \) ( \( K_2 = K_a \) )
3. \( \text{H}_2\text{O} \rightleftharpoons \text{H}^+ + \text{OH}^- \) ( \( K_w \) )
To obtain the desired reaction, we combine the first and second reactions:
\[ \text{La}^{3+} + \text{CO}_3^{2-} + \text{H}_2\text{O} \rightleftharpoons \text{LaCO}_3^+ + \text{OH}^- + \text{H}^+ \]
Multiplying the equilibrium constant expressions:
\[ K_1 \times K_a = \frac{[\text{LaCO}_3^+][\text{H}_2\text{O}]}{[\text{La}^{3+}][\text{OH}^-][\text{HCO}_3^-]} \times \frac{[\text{H}^+][\text{CO}_3^{2-}]}{[\text{HCO}_3^-]} \]
\[ = \frac{[\text{LaCO}_3^+][\text{H}^+][\text{CO}_3^{2-}]}{[\text{La}^{3+}][\text{OH}^-]} \]
To eliminate \( [\text{OH}^-] \), we use \( K_w \):
\[ K_w = [\text{H}^+][\text{OH}^-] \]
\[ [\text{OH}^-] = \frac{K_w}{[\text{H}^+]} \]
Substituting into the previous expression:
\[ K_1 \times K_a = \frac{[\text{LaCO}_3^+][\text{H}^+][\text{CO}_3^{2-}]}{[\text{La}^{3+}][\frac{K_w}{[\text{H}^+]}]} \]
\[ = \frac{[\text{LaCO}_3^+][\text{H}^+]^2[\text{CO}_3^{2-}]}{[\text{La}^{3+}]K_w} \]
For the desired reaction \( \text{La}^{3+} + \text{CO}_3^{2-} \rightleftharpoons \text{LaCO}_3^+ \), we have:
\[ K = \frac{[\text{LaCO}_3^+]}{[\text{La}^{3+}][\text{CO}_3^{2-}]} \]
Therefore,
\[ K = \frac{(K_1 \times K_a \times [\text{H}^+]^2)}{K_w} \]
The correct answer is thus \( (D) \) \( K = \frac{(K_1 \times K_w)}{K_a} \).
Question
Step 1: \(H_2O_2+I^−→IO^−+H_2O\)
Step 2: \(H_2O_2+IO^−→H_2O+O_2+I^−\)
The mechanism for a chemical reaction is shown above. Which of the following statements about the overall reaction and rate laws of the elementary reactions is correct?
A The chemical equation for the overall reaction is \(2H_2O_2+I^−→ 2H_2O+O_2+I^−\) , and the rate law for elementary step 2 is rate=\(k[H_2O_2][IO^−]\) .
B The chemical equation for the overall reaction is \(H_2O_2+IO^−→ H_2O+O_2+I^−\) , and the rate law for elementary step 2 is rate=\(k[H_2O_2]^2[IO^−]\) .
C The chemical equation for the overall reaction is \(2H_2O_2→2H_2O+O_2\) , and the rate law for elementary step 1 is rate=\(k[H_2O_2][I^−]\) .
D The chemical equation for the overall reaction is \(2H_2O_2→2H_2O+O_2\) , and the rate law for elementary step 1 is rate=\(k[H_2O_2]^2\).
▶️Answer/Explanation
Ans:C
Once all the elementary steps are added and simplified, the resulting equation is \(2H_2O_2→2H_2O+O_2\). Because a rate law for an elementary step can be based on the stoichiometric coefficients of the reactants in that step, the rate law for elementary step 1 is rate=\(k[H_2O_2][I^−]\), and the rate law for elementary step 2 is rate=\(k[H_2O_2][IO^−]\).
Question
Step 1: \(N_2O_5→NO_2+NO_3\) (slow)
Step 2: \(NO_2+NO_3→NO_2+NO+O_2\) (fast)
Step 3: \(NO+N_2O_5→3NO_2\) (fast)
A proposed reaction mechanism for the decomposition of N2O5(g) is shown above. Based on the proposed mechanism, which of the following correctly identifies both the chemical equation and the rate law for the overall reaction?
A The chemical equation for the overall reaction is \(NO+N_2O_5→3NO_2\) , and the rate law is rate=\(k[NO][N_2O_5]\).
B The chemical equation for the overall reaction is \(2N_2O_5(g)→4NO_2(g)+O_2(g)\) , and the rate law is rate=\(k[N_2O_5]\).
C The chemical equation for the overall reaction is \(2N_2O_5(g)→4NO_2(g)+O_2(g)\) , and the rate law is rate=\(k[N_2O_5]^2 \).
D The chemical equation for the overall reaction is \(N_2O_5(g)+NO(g)+NO_3(g)→4NO_2(g)+O_2(g)\) , and the rate law is rate=\(k[N_2O_5][NO][NO_3]\).
▶️Answer/Explanation
Ans:B
When the elementary steps are added and simplified, the net chemical equation for the overall reaction is 2N2O5(g)→4NO2(g)+O2(g) . Because step 1 is the slowest (rate-determining) step, rate=\([N_2O_5]\).
Question
Step 1: ? (slow)
Step 2: \(NO_2(g)+F(g)→NO_2F(g)\) (fast)
Overall: 2 \(NO_2(g)+F_2(g)→2NO_2F(g)\)
The overall reaction represented above is proposed to take place through two elementary steps. Which of the following statements about the chemical equation for step 1 and the rate law for the overall reaction is correct?
A The chemical equation for step 1 is \(NO_2(g)+F_2(g)→NO_2F(g)+F(g)\) , and the rate law for the overall reaction is rate=\(k[NO_2][F_2]\).
B The chemical equation for step 1 is \(NO_2(g)+F(g)→NO_2F(g)+F_2(g)\) , and the rate law for the overall reaction is rate=\(k[NO_2][F]\).
C The chemical equation for step 1 is \(2NO_2(g)+F_2(g)→2NO_2F(g)\) , and the rate law for the overall reaction is rate=\(k[NO_2][F]\).
D The chemical equation for step 1 is \(3NO_2(g)+F_2(g)+F(g)→3NO_2F(g)\), and the rate law for the overall reaction is rate=\(k[NO_2]^2[F_2]\).
▶️Answer/Explanation
Ans: A
The chemical equations for the two elementary steps should add up to give the net equation for the overall reaction. Based on the chemical equations for step 2 and the overall reaction, the chemical equation for step 1 is \(NO_2(g)+F_2(g)→NO_2F(g)+F(g)\). Because step 1 is the slow (rate-determining) step, the rate law for the overall reaction is set by the stoichiometry of step 1 and is equal to rate=\(k[NO_2][F_2]\).
Question
For the elementary reaction
\(NO_3 + CO \rightarrow NO_2 + CO_2\)
the molecularity of the reaction is __________, and the rate law is rate = __________.
A) 4, \(k[NO_3][CO][NO_2][CO_2]\)
B) 2, \(k[NO_3][CO]/[NO_2][CO_2]\)
C) 4, \(k[NO_2][CO_2]/[NO_3][CO]\)
D) 2, \(k[NO_2][CO_2]\)
E) 2, \(k[NO_3][CO]\)
▶️Answer/Explanation
Ans: E

Question
The kinetics of the reaction below were studied and it was determined that the reaction rate increased by a
factor of 9 when the concentration of B was tripled. The reaction is __________ order in B.
\(A + B \rightarrow P\)
A) zero B) first C) second D) third E) one-half
▶️Answer/Explanation
Ans: C