Question
A 50.0 g sample of Feat 100°C is added to 500.0 mL of water at 35°C in a perfectly insulated container. Which of the following statements is true?
(A) The temperature of the water will decrease.
(B) The temperature change of the Fe will have the same magnitude as the temperature change of the water.
(C) The heat energy lost by the Fe will be less than the heat energy gained by the water.
(D) The heat energy lost by the Fe will be equal to the heat energy gained by the water
▶️Answer/Explanation
.Ans:D
When the iron is added to the water, heat will transfer from the iron to the water until thermal equilibrium is reached.
\[ q = mc\Delta T \]
For iron (\( Fe \)):
\[ m_{Fe} = 50.0 \, \text{g} \]
\[ c_{Fe} = 0.449 \, \text{J/(g°C)} \] (specific heat capacity of iron)
\[ \Delta T_{Fe} = T_{\text{final, Fe}} – T_{\text{initial, Fe}} = T_{\text{final, Fe}} – 100°C \]
For water:
\[ m_{\text{water}} = 500.0 \, \text{g} \]
\[ c_{\text{water}} = 4.18 \, \text{J/(g°C)} \] (specific heat capacity of water)
\[ \Delta T_{\text{water}} = T_{\text{final, water}} – T_{\text{initial, water}} = T_{\text{final, water}} – 35°C \]
Now, let’s calculate the heat lost by the iron and gained by the water:
\[ q_{Fe} = m_{Fe} \times c_{Fe} \times \Delta T_{Fe} \]
\[ q_{\text{water}} = m_{\text{water}} \times c_{\text{water}} \times \Delta T_{\text{water}} \]
Since energy is conserved, \( q_{Fe} = -q_{\text{water}} \).
Now, let’s analyze each statement:
(A) The temperature of the water will decrease.
True. Since heat transfers from the iron to the water, the temperature of the water will decrease.
(B) The temperature change of the Fe will have the same magnitude as the temperature change of the water.
False. The temperature change of the iron (\( \Delta T_{Fe} \)) will be different from the temperature change of the water (\( \Delta T_{\text{water}} \)) because the specific heat capacities are different.
(C) The heat energy lost by the Fe will be less than the heat energy gained by the water.
False. The heat energy lost by the iron will be equal in magnitude but opposite in sign to the heat energy gained by the water.
(D) The heat energy lost by the Fe will be equal to the heat energy gained by the water.
True. This statement is consistent with the principle of conservation of energy. The heat lost by the iron will be equal in magnitude but opposite in sign to the heat gained by the water.
Therefore, the correct answer is:(D).
Question
\(AgNO_{3}(aq)+NaCl(aq) \rightarrow AgCl(s)+NaNO_{3}\)(aq)
In an experiment a student mixes a 50.0 mL sample of 0.100 M \(AgNO_{3}\)(aq) with a 50.0 mL sample of 0.100 M NaCl(aq) at 20.0°C in a coffee-cup calorimeter. Which of the following is the enthalpy change of the precipitation reaction represented above if the final temperature of the mixture is 21.0°C? (Assume that the total mass of the mixture is 100. g and that the specific heat capacity of the mixture is 4.2 J/(g °C).)
(A) \(−84 kJ/mol_{rxn}\)
(B) \(−0.42 kJ/mol_{rxn}\)
(C) \(0.42 kJ/mol_{rxn}\)
(D) \(84 kJ/mol_{rxn}\)
▶️Answer/Explanation
Ans:C
Given:
Mass of the solution (\(m\)) = 100.0 g
Specific heat capacity of the solution (\(c\)) = 4.2 J/(g°C)
Change in temperature (\(\Delta T\)) = 1.0°C
Using the equation:
\[ q = m \times c \times \Delta T \]
\[ q = (100.0 \, \text{g}) \times (4.2 \, \text{J/(g°C)}) \times (1.0 \, \text{°C}) \]
\[ q = 420 \, \text{J} \]
To convert from joules to kilojoules:
\[ \Delta H = \frac{420 \, \text{J}}{1000 \, \text{J/kJ}} = 0.42 \, \text{kJ} \]
So, the enthalpy change of the precipitation reaction is indeed \(0.42 \, \text{kJ}\).
The correct answer is indeed:
(C) \(0.42 \, \text{kJ/mol}_{\text{rxn}}\)
Questions
When 5.0 g of \(NH^{4}ClO_{4(s)}\) is added to 100. mL of water in a calorimeter, the temperature of the solution formed decreases by 3.0\(^{\circ }C\). If 5.0 g of \(NH^{4}ClO_{4(s)}\) is added to 1000. mL of water in a calorimeter initially at 25.0\(^{\circ }C\), the final temperature of the solution will be approximately
(A) 22.0\(^{\circ }C\)
(B) 24.7\(^{\circ }C\)
(C) 25.3\(^{\circ }C\)
(D) 28.0\(^{\circ }C\)
▶️Answer/Explanation
Ans: B
Given:
When \(5.0 \, \text{g}\) of \(NH_4ClO_4(s)\) is added to \(100 \, \text{mL}\) of water, the temperature of the solution decreases by \(3.0^\circ C\).
The question asks about the final temperature when \(5.0 \, \text{g}\) of \(NH_4ClO_4(s)\) is added to \(1000 \, \text{mL}\) of water initially at \(25.0^\circ C\).
We can assume that the heat of solution for \(NH_4ClO_4(s)\) is an endothermic process, meaning that the dissolution absorbs heat from the surroundings, causing the temperature of the solution to decrease.
Since the temperature change is proportional to the amount of heat absorbed or released, and the heat of solution is a constant for a given compound, we can use the following relationship:
\[
\frac{\text{Temperature change for 100 mL of water}}{\text{Temperature change for 1000 mL of water}} = \frac{100 \, \text{mL}}{1000 \, \text{mL}} = \frac{1}{10}
\]
Therefore, the temperature change for \(1000 \, \text{mL}\) of water will be one-tenth of the temperature change for \(100 \, \text{mL}\) of water.
Given:
Temperature change for \(100 \, \text{mL}\) of water = \(-3.0^\circ C\)
Temperature change for \(1000 \, \text{mL}\) of water = \((-3.0^\circ C) \times \frac{1}{10} = -0.3^\circ C\)
Initial temperature of the solution = \(25.0^\circ C\)
Final temperature of the solution = Initial temperature + Temperature change
Final temperature of the solution = \(25.0^\circ C – 0.3^\circ C = 24.7^\circ C\)
Question

The graph above shows the changes in temperature recorded for the 2.00 L of H2O surrounding a constant-volume container in which a 1.00 g sample of benzoic acid was combusted. Assume that heat was not absorbed by the container or lost to the surroundings, that the density of H2O is 1.00g/mL, and that the specific heat capacity of H2O is about 4.2J/g⋅°C. Based on this information, estimate how much heat was released from the combustion of the benzoic acid sample.
A 0.013kJ
B 25kJ
C 180kJ
D 210kJ
▶️Answer/Explanation
Ans:B
The heat released from the combustion of benzoic acid was absorbed by the water and can be calculated by q=mcΔT . Estimating from the graph that the temperature change for the water was about 3.0°C and using 2000g as the mass of the water gives q=(2000g)×(4.2J/g⋅°C)×3.0°C=25,200 J, which is approximately equal to 25kJ.
Question

For an experiment, a 20.0 g piece of \(Al\) was placed inside an insulated cup filled with 40.0 g of \(H_2O\). The data are given in the table above. Assuming no heat is absorbed by the container or the surroundings, which of the following equations provides the correct mathematical relationship for the transfer of heat q between \(Al\) and \(H_2O\)?
A \(−q_{Al}=10\times q_{H_2O}\)
B \(−q_{Al}=5\times q_{H_2O}\)
C \(−q_{Al}=2\times q_{H_2O}\)
D \(−q_{Al}=q_{H_2O}\)
▶️Answer/Explanation
Ans:D
Since heat is only transferred between Al and \(H_2O\), based on the law of conservation of energy, the amount of thermal energy (heat) released by Al must equal the amount of heat absorbed by \(H_2O\) , or \(−q_{Al}=q_{H_2O}\).
Question
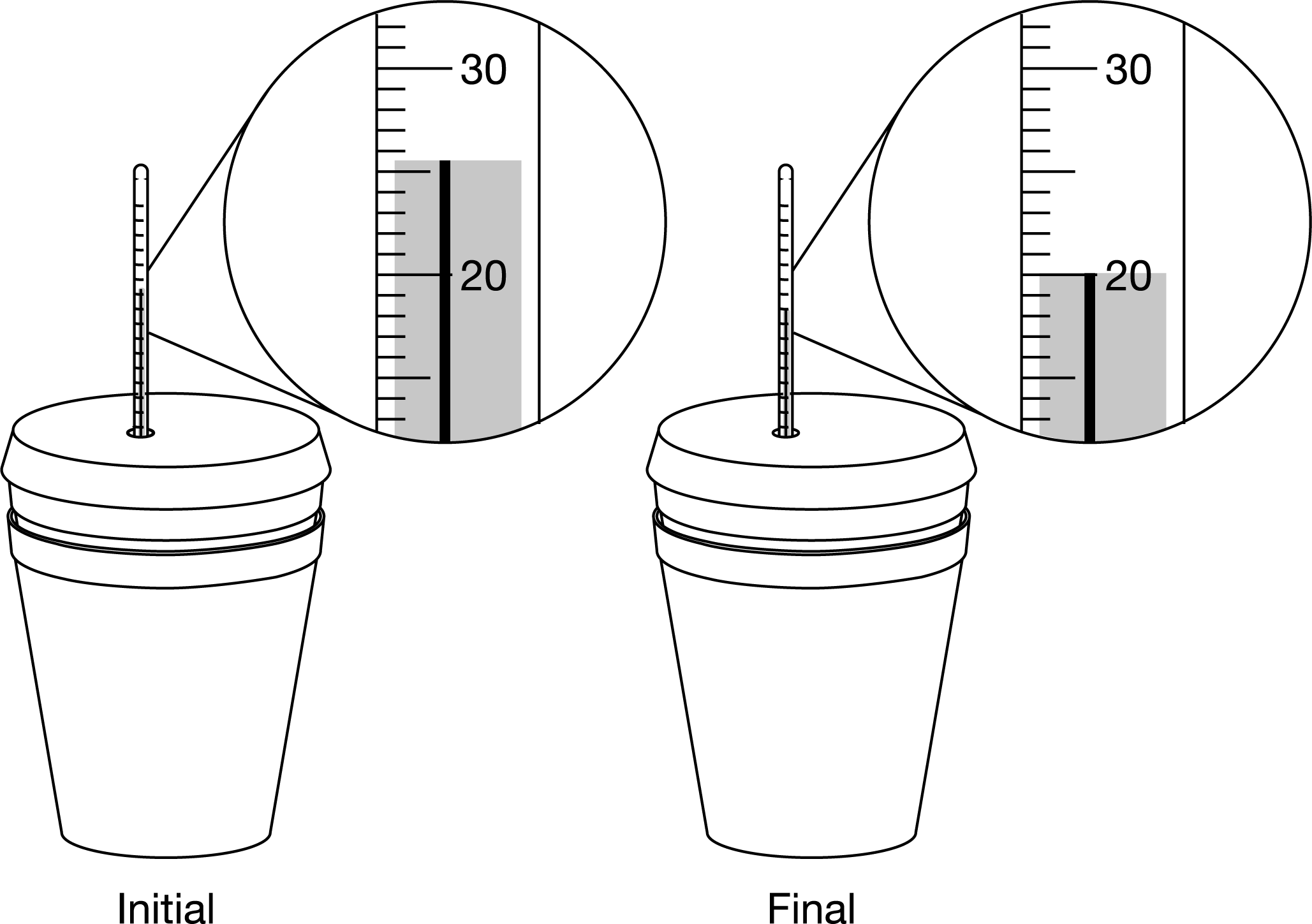
A student dissolves 8.00 g of \(NH_4NO_3\)(s) in 100. g of \(H_2O(l)\) in a coffee-cup calorimeter. Based on the initial and final temperatures of the mixture in degrees Celsius shown in the diagram above the laboratory setup, what is the calculated ΔTof the water reported to the appropriate number of significant figures?
A −5.500°C
B −5.50°C
C −5.5°C
D −6°C
▶️Answer/Explanation
Ans:C
Based on the scale of the thermometer, the temperature can be read to the nearest marked gradation, or if possible, halfway between. Because the initial temperature reading is 25.5°C
and the final temperature reading is 20.0°C, the reported change in temperature with the correct number of significant figures is 5.5°C.
Question
Refer to the following graph, which shows the heating curve for methane, \(CH_4\)
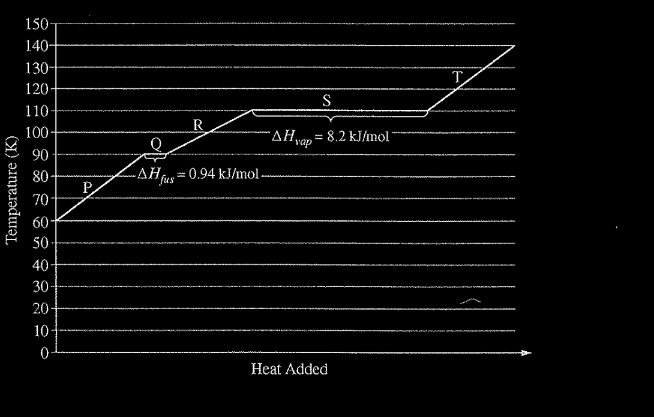
How much energy is required to melt 64 g of methane at 90 K? (The molar mass of methane is 16 g/mol.)
(A) 0.24 kJ
(B) 3.8 kJ
(C) 33 kJ
(D) 60. kJ
▶️Answer/Explanation
Ans:B
Question
\(NaOH(aq)+HCl(aq) \rightarrow NaCl(aq)+H_{2}O(l)\)
To determine the concentration of a NaOH(aq) solution, a student titrated a 50. mL sample with 0.10 M HCl(aq). The reaction is represented by the equation above. The titration is monitored using a pH meter, and the experimental results are plotted in the graph below.
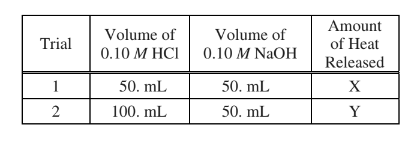
A student conducted an experiment to determine \(\Delta H^{\circ}_{rxn}\) the reaction between HCl(aq) and NaOH(aq). The student ran two trials using the volumes of HCl(aq) and NaOH(aq) indicated in the table above, and determined the amount of heat released. Which of the following best explains the relationship between X and Y?
(A) Y = 2X, because the volume of HCl(aq) used in trial 2 is twice the volume used in trial 1.
(B) Y = X, because the number of moles of acid and bas reacting with each other is the same in both trials.
(C) \(Y=\frac{2X}{3}\),because the heat is distributed over more particles in trial 2 than in trial 1.
(D) The relationship between X and Y cannot be predicted.
▶️Answer/Explanation
Ans:D