Questions
\(X_{2}+Y_{2}(g)\rightleftharpoons 2XY(g) k_{c}=3.0\)
A mixture of\( X_{2}\)(g), \(Y_2\)(g), and XY(g) is placed in a previously evacuated, rigid container and allowed to reach equilibrium at a constant temperature, as shown above. Which of the following sets of initial concentrations would lead to the formation of more product as the system moves toward equilibrium?

▶️Answer/Explanation
Ans: A
To determine which set of initial concentrations would lead to the formation of more product as the system moves toward equilibrium, we need to consider Le Chatelier’s Principle.
Given the equilibrium reaction:
\[X_{2} + Y_{2}(g) \rightleftharpoons 2XY(g) \]
The equilibrium constant \(Kc\) is given as \(3.0\).
When the system is at equilibrium, the ratio of the concentrations of products to reactants should equal \(Kc\):
\[ \frac{[\text{XY}]^2}{[\text{X}_2][\text{Y}_2]} = K_c \]
Given the initial concentrations, we can calculate the reaction quotient \(c\) for each set of initial concentrations and compare it to \(Kc\) to determine which set will favor the formation of more product.
(A)
\[ Q_c = \frac{(0.20)^2}{(0.40)(0.40)} = 0.25 \]
(B)
\[ Q_c = \frac{(0.90)^2}{(0.30)(0.30)} = 9.00 \]
(C)
\[ Q_c = \frac{(0.30)^2}{(0.15)(0.15)} = 4.00 \]
(D)
\[ Q_c = \frac{(0.20)^2}{(0.10)(0.10)} = 4.00 \]
Comparing the values of \(Q_c\) to \(K_c = 3.0\):
For set (A): \(Q_c < K_c\)
For set (B): \(Q_c > K_c\)
For set (C): \(Q_c > K_c\)
For set (D): \(Q_c > K_c\)
According to Le Chatelier’s Principle, if \(Q_c\) is less than \(K_c\), the reaction will shift to the right to reach equilibrium, favoring the formation of more product. Therefore, set (A) will lead to the formation of more product as the system moves toward equilibrium.
Question
\(H_{2}(g)+I_{2}(g)\rightleftharpoons 2HI(g)\) \( K_{c}=50.at 600^{\circ}C\)
Equimolar samples of each of three gases, \(H_2\)(g), \(I_2\)(g), and HI(g), are introduced into a 3.0 L container that is heated to 600°C. According to the information above, which of the following will occur as the system approaches equilibrium?
(A) More \(H_2\)(g) will be produced because Q > Kc .
(B) More \(I_2\)(g) will be produced because Q < Kc .
(C) More HI(g) will be produced because Q <\( K_c\) .
(D) No change will occur because Q = \(K_c\) .
▶️Answer/Explanation
Ans:C
The correct answer is More HI(g) will be produced because Q < (K_c).
The reaction quotient Q is calculated in the same way as the equilibrium constant K, but Q can be calculated at any point in time, not just at equilibrium. For the reaction \(H_{2}(g)+I_{2}(g)\rightleftharpoons 2HI(g)\), the expression for Q is:
\[Q = \frac{[HI]^2}{[H_{2}][I_{2}]}\]
Given that equimolar samples of (H_{2}), (I_{2}), and HI are introduced into the container, the initial concentrations of each species are the same. Therefore, Q = 1.
Since (K_c) for the reaction at 600°C is 50, which is greater than Q (Q < (K_c)), the reaction will shift to the right to reach equilibrium. This means more HI(g) will be produced. Therefore, option C is correct.
Question
\[
\mathrm{Li}_3 \mathrm{~N}(s)+2 \mathrm{H}_2(g) \rightleftarrows \mathrm{LiNH}_2(s)+2 \mathrm{LiH}(s) \quad \Delta H^{\circ}=-192 \mathrm{~kJ} / \mathrm{mol}_{r x n}
\]
Because pure \(\mathrm{H}_2\) is a hazardous substance, safer and more cost effective techniques to store it as a solid for shipping purposes have been developed. One such method is the reaction represented above, which occurs at \(200^{\circ} \mathrm{C}\).
The amount of\( H_2\)(g) present in a reaction mixture at equilibrium can be maximized by
(A) increasing the temperature and increasing the pressure by decreasing the volume
(B) increasing the temperature and decreasing the pressure by increasing the volume
(C) decreasing the temperature and increasing the pressure by decreasing the volume
(D) decreasing the temperature and decreasing the pressure by increasing the volume
▶️Answer/Explanation
Ans:C
\[ \mathrm{Li}_3 \mathrm{~N}(s) + 2 \mathrm{H}_2(g) \rightleftarrows \mathrm{LiNH}_2(s) + 2 \mathrm{LiH}(s) \]
This reaction involves the decomposition of lithium amide (\( \mathrm{Li}_3 \mathrm{N} \)) and the formation of lithium imide (\( \mathrm{LiNH}_2 \)) and lithium hydride (\( \mathrm{LiH} \)).
From the stoichiometry of the reaction, we can see that \( 2 \) moles of \( H_2(g) \) are consumed to form the products. According to Le Chatelier’s Principle, to maximize the amount of \( H_2(g) \) present in the equilibrium mixture, we need to shift the equilibrium to the left, favoring the formation of more reactants.
Now, let’s analyze the given options:
(A) Increasing the temperature and increasing the pressure by decreasing the volume: This would likely favor the forward reaction according to Le Chatelier’s Principle because the forward reaction is endothermic (heat is absorbed). Therefore, this option would not maximize the amount of \( H_2(g) \) present in the equilibrium mixture.
(B) Increasing the temperature and decreasing the pressure by increasing the volume: Increasing the temperature would favor the endothermic reaction, but decreasing the pressure would not favor the formation of more reactants because there are fewer moles of gas on the reactant side compared to the product side. So, this option would also not maximize the amount of \( H_2(g) \) present.
(C) Decreasing the temperature and increasing the pressure by decreasing the volume: Decreasing the temperature would favor the exothermic reaction (the reverse reaction), and increasing the pressure by decreasing the volume would favor the side with fewer moles of gas molecules, which is the reactant side in this case. This option would shift the equilibrium to the left, favoring the formation of more \( H_2(g) \). Therefore, this option seems promising.
(D) Decreasing the temperature and decreasing the pressure by increasing the volume: Similar to option (B), decreasing the pressure would not favor the formation of more reactants, so this option would not maximize the amount of \( H_2(g) \) present.
Therefore, the correct answer is:
(C) Decreasing the temperature and increasing the pressure by decreasing the volume.
Questions
\(3O_{2(g)}\leftrightharpoons 2O_{3(g)}\) \( K_{c}=1.8\times 10^{-56}\) at 570 K
For the system represented above, [\(O_{2}\)] and [\(O_{3}\)] initially are 0.150 mol/L and 2.5 mol/L respectively. Which of the following best predicts what will occur as the system approaches equilibrium at 570 K?
(A) The amount of \(O_{3(g)}\) will increase, because Q < Kc.
(B) The amount of \(O_{3(g)}\) will decrease, because Q < K.
(C) The amount of \(O_{3(g)}\) will increase, because Q > Kc.
(D) The amount of \(O_{3(g)}\) will decrease, because Q > Kc.
▶️Answer/Explanation
Ans: D
To solve this problem, we need to calculate the reaction quotient (Q) using the given initial concentrations of \( O_2 \) and \( O_3 \), and then compare \( Q \) with the equilibrium constant (\( K_c \)) to predict the direction of the reaction.
The reaction quotient, \( Q \), is given by:
\[ Q = \frac{{[O_3]^2}}{{[O_2]^3}} \]
Substituting the given initial concentrations, we get:
\[ Q = \frac{{(2.5 \, \text{mol/L})^2}}{{(0.150 \, \text{mol/L})^3}} \]
\[ Q = \frac{{6.25}}{{0.003375}} \]
\[ Q = 1852.78 \]
Since \( Q > K_c \) (1852.78 > \( 1.8 \times 10^{-56} \)), the system is not at equilibrium, and the reaction will proceed in the reverse direction to achieve equilibrium.
Therefore, the correct answer is: (D) The amount of \( O_3(g) \) will decrease, because \( Q > K_c \).
The system will consume \( O_3 \) and produce \( O_2 \) to decrease the concentration of \( O_3 \) and increase the concentration of \( O_2 \) until \( Q = K_c \) at equilibrium.
Question
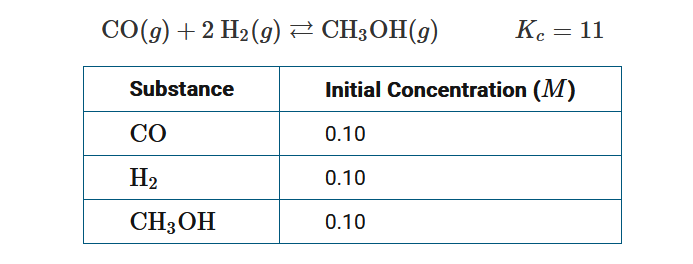
The table lists the initial concentrations of each substance in the system represented by the equation above at a given temperature. Which of the following best predicts what will occur as the system approaches equilibrium?
A The rate of the reverse reaction will be less than the rate of the forward reaction, and additional \(CH_3OH\)(g) will be consumed because \(K_c<Q_c\) .
B The rate of the reverse reaction will be greater than the rate of the forward reaction, and additional \(CH_3OH\)(g) will be consumed because \(K_c<Q_c\) .
C The rate of the forward reaction will be less than the rate of the reverse reaction and, additional \(CH_3OH\)(g) will be produced because \(K_c<Q_c\) .
D The rate of the forward reaction will be greater than the rate of the reverse reaction, and additional \(CH_3OH\)(g) will be produced because \(K_c<Q_c\).
▶️Answer/Explanation
Ans:B
\(Q_c=\frac{[CH_3OH]}{[CO][H_2]^2}=\frac{(0.10)}{(0.10)(0.10)^2}=100\) , and when \(K_c<Q_c\), the rate of the reverse reaction will be greater than the rate of the forward reaction, resulting in the net consumption of CH3OH(g) until equilibrium is reached.
Question
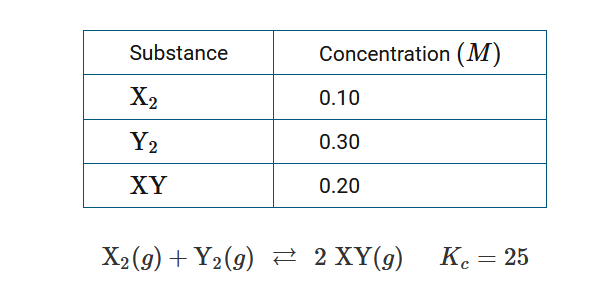
The chemical reaction shown above took place inside a rigid container at constant temperature. The table provides the concentrations of reactants and products at some point during the reaction. Based on this information, which of the following explains whether or not the reaction has reached equilibrium, and why?
A The reaction is not at equilibrium because \(Q_c>K_c\) ; the forward reaction is favored in order to form more XY .
B The reaction is not at equilibrium because \(Q_c<K_c\) ; the reverse reaction is favored in order to form more \(X_2\) and \(Y_2\) .
C The reaction is not at equilibrium because \(Q_c<K_c\) ; the forward reaction is favored in order to form more XY .
D The reaction is at equilibrium because \(Q_c=K_c\) ; the amount of \(X_2\), \(Y_2\) and XY will remain the constant.
▶️Answer/Explanation
Ans:C
The expressions for \(Q_c\) and \(K_c\) are similar: \(Q_c=\frac{[XY]^2}{[X_2][Y_2]}=\frac{(0.20)^2}{(0.10)(0.30)}\)≈1.3. When \(Q_c<K_c\), the reaction is not at equilibrium and will favor the forward reaction to form additional XY.
Question
\(COCl_2(g)\)⇄\(CO(g)+Cl_2(g)\)
At a given temperature, the system represented by the chemical equation above is at equilibrium inside a rigid container. Which of the following explains how the system will restore equilibrium, based on the correct relationship between Q and K, after a certain amount of \(Cl_2\)(g) is added?
A Since \(Q=\frac{[Cl2][CO]}{[COCl_2]}\) , \(Q>K\) when \(Cl_2\)(g) is added to the system; the system will restore equilibrium by producing more \(COCl_2(g)\) .
B Since \(Q=\frac{[Cl2][CO]}{[COCl_2]}\) , \(Q<K\) when \(Cl_2\)(g) is added to the system; the system will restore equilibrium by producing more \(CO(g)\) .
C Since \(Q=\frac{[COCl_2]}{[Cl2][CO]}\) , \(Q>K\) when \(Cl_2\)(g) is added to the system; the system will restore equilibrium by producing more \(COCl_2(g)\) .
D Since \(Q=\frac{[COCl_2]}{[Cl2][CO]}\) , \(Q>K\) when \(Cl_2\)(g) is added to the system; the system will restore equilibrium by producing more \(CO(g)\) .
▶️Answer/Explanation
Ans:A
Based on the mathematical expression for Q , \(Q=\frac{[Cl2][CO]}{[COCl_2]}\), the addition of \(Cl_2\) increases the numerator in this ratio, which increases the magnitude of Q overall. When \(Q>K\), the system will restore equilibrium by increasing the rate of the reverse reaction in the equilibrium and more \(COCl_2\) will be produced.
Question
\(PC1_3(g) + Cl_2(g) \rightleftharpoons PCl_{5}(g)\) \( K_{c} 6.5\)
36. At a certain point in time, a 1.00 L rigid reaction vessel contains 1.5 mol of PCl,(g), 1.0 mol of \(Cl_2\)(g), and 2.5 mol of\( PCl_5\)(g). Which of the following describes how the measured pressure in the reaction vessel will change and why it will change that way as the reaction system approaches equilibrium at constant temperature?
(A) The pressure will increase because \(Q< K_c\)
(B) The pressure will increase because \(Q > K_c\)
(C) The pressure will decrease because \(Q< K_c\)
(D) The pressure will decrease because \(Q > K_c\)
▶️Answer/Explanation
Ans:C
Question
\(3O_{2}(g)\rightleftharpoons 2O_{3}(g) \) \(K_{c}=1.8\times 10^{-56}\)at 570k
For the system represented above, [\(O_{2}\)] and \([O_{3}]\) initially are 0.150 mol/L and 2.5 mol/L respectively. Which of the following best predicts what will occur as the system approaches equilibrium at 570 K?
(A) The amount of\( O_{3}\)(g) will increase, because Q<K
(B) The amount of \(O_{3}\)(g) will decrease, because Q<K
(C) The amount of \(O_{3}\)(g) will increase, because Q> K
(D) The amount of \(O_{3}\)(g) will decrease, because Q>K
▶️Answer/Explanation
Ans:C