Question
\(HCHO_{2}(aq)+H_{2}O(l)\rightleftharpoons H_{3}O^{+}(aq)+CHO_{2}^{-}(aq)\)
\(HCHO_2\)(aq), a weak acid (K = \(2 × 10^{−4})\) a , dissociates in water according to the equation above. Which of the following provides the best estimate of the pH of 0.5 M \(HCHO_2\)(aq) and identifies the species at the highest concentration (excluding\( H_2O)\) in the solution?

▶️Answer/Explanation
Ans:D
The dissociation of a weak acid in water can be represented as follows:
\[ HA(aq) \rightleftharpoons H^{+}(aq) + A^{-}(aq) \]
The equilibrium constant expression for this reaction is:
\[ K_a = \frac{[H^{+}][A^{-}]}{[HA]} \]
Given that \( K_a = 2 \times 10^{-4} \) and the initial concentration of \( HCHO_2 \) is 0.5 M, we can set up the following table to represent the concentrations of the species at equilibrium:
\[
\begin{array}{lccc}
& \text{Initial Concentration} & \text{Change in Concentration} & \text{Equilibrium Concentration} \\
HCHO_2 & 0.5 & -x & 0.5 – x \\
H^{+} & 0 & +x & x \\
CHO_2^{-} & 0 & +x & x \\
\end{array}
\]
Substituting these into the \( K_a \) expression gives:
\[ 2 \times 10^{-4} = \frac{x^2}{0.5 – x} \]
Assuming that \( x << 0.5 \), we can approximate \( 0.5 – x \approx 0.5 \), which simplifies the equation to:
\[ x = \sqrt{2 \times 10^{-4} \times 0.5} \approx 0.01 \]
The \( H^{+} \) ion concentration is equal to \( x \), so the pH of the solution is \( -\log[H^{+}] = -\log(0.01) = 2 \).
Since \( HCHO_2 \) is a weak acid, it does not fully dissociate in water. Therefore, at equilibrium, the concentration of \( HCHO_2 \) will be higher than the concentrations of \( H^{+} \) and \( CHO_2^{-} \). Thus, the species at the highest concentration (excluding \( H_2O \)) in the solution is \( HCHO_2 \).
Question
The pH of a solution made by combining 150.0 mL of 0.10 M KOH(aq) with 50.0 mL of 0.20 M\( HBr(aq)\) is closest to which of the following?
(A) 2
(B) 4
(C) 7
(D) 12
▶️Answer/Explanation
Ans:D
To find the pH of the resulting solution, we need to first determine the moles of \( OH^{-} \) and \( H^{+} \) ions produced by the reaction between \( KOH \) and \( HBr \).
From the given concentrations and volumes, we can calculate the moles of each species:
For \( KOH \):
\[
\text{Moles of } OH^{-} = \text{Molarity} \times \text{Volume} = 0.10 \, \text{M} \times 0.150 \, \text{L} = 0.015 \, \text{mol}
\]
For \( HBr \):
\[
\text{Moles of } H^{+} = \text{Molarity} \times \text{Volume} = 0.20 \, \text{M} \times 0.050 \, \text{L} = 0.010 \, \text{mol}
\]
Since \( KOH \) and \( HBr \) react in a 1:1 ratio according to the balanced equation:
\[ KOH(aq) + HBr(aq) \rightarrow KBr(aq) + H_2O(l) \]
Therefore, the moles of \( OH^{-} \) in excess are \( 0.015 \, \text{mol} – 0.010 \, \text{mol} = 0.005 \, \text{mol} \).
We then convert the excess moles of \( OH^{-} \) to \( \text{pOH} \):
\[ \text{pOH} = -\log(\text{OH}^-) = -\log(0.005 \, \text{M}) \]
\[ \text{pOH} \approx 2.3 \]
Finally, we can find the pH using the relation:
\[ \text{pH} + \text{pOH} = 14 \]
\[ \text{pH} = 14 – \text{pOH} = 14 – 2.3 \]
\[ \text{pH} \approx 11.7 \]
Since the closest option is 12, the correct answer is: (D) 12
Question
\(HN0_{2}(aq)\rightleftharpoons H^{+}N0_{2}^{-}(aq)\) \(K_{a}=4.0\times 10^{-4}\)
On the basis of the information above, what is the approximate percent ionization of \(HNO_{2}\) in a 1.0 M\( HNO_{2}\)(aq) solution?
(A) 0.00040%
(B) 0.020%
(C) 0.040%
(D) 2.0%
▶️Answer/Explanation
Ans:D
To find the percent ionization of \(HNO_2\) in a 1.0 M \(HNO_2(aq)\) solution, we need to use the given equilibrium constant (\(K_a\)) and the initial concentration of \(HNO_2\).
The equilibrium constant \(K_a\) is given as \(4.0 \times 10^{-4}\).
For a weak acid like \(HNO_2\), the percent ionization is low, so we can assume that the concentration of the ionized species (\(H^+\) and \(NO_2^-\)) is much smaller than the initial concentration of \(HNO_2\). This assumption allows us to use the approximation:
\([H^+] = [NO_2^-] = x\) (let’s call this the ionization concentration)
\([HNO_2] \approx 1.0\) M (the initial concentration)
Substituting these values into the equilibrium constant expression:
\[ K_a = \frac{[H^+][NO_2^-]}{[HNO_2]} \]
\[ 4.0 \times 10^{-4} = \frac{x^2}{1.0} \]
Solving for \(x\):
\[ x^2 = 4.0 \times 10^{-4} \]
\[ x = \sqrt{4.0 \times 10^{-4}} = 0.02 \text{ M} \]
This means that the ionization concentration \([H^+] = [NO_2^-] = 0.02\) M.
To find the percent ionization, we divide the ionization concentration by the initial concentration and multiply by 100:
\[ \text{Percent ionization} = \left( \frac{0.02 \text{ M}}{1.0 \text{ M}} \right) \times 100\% = 2\% \]
Therefore, the correct answer is (D) 2.0%.
Question
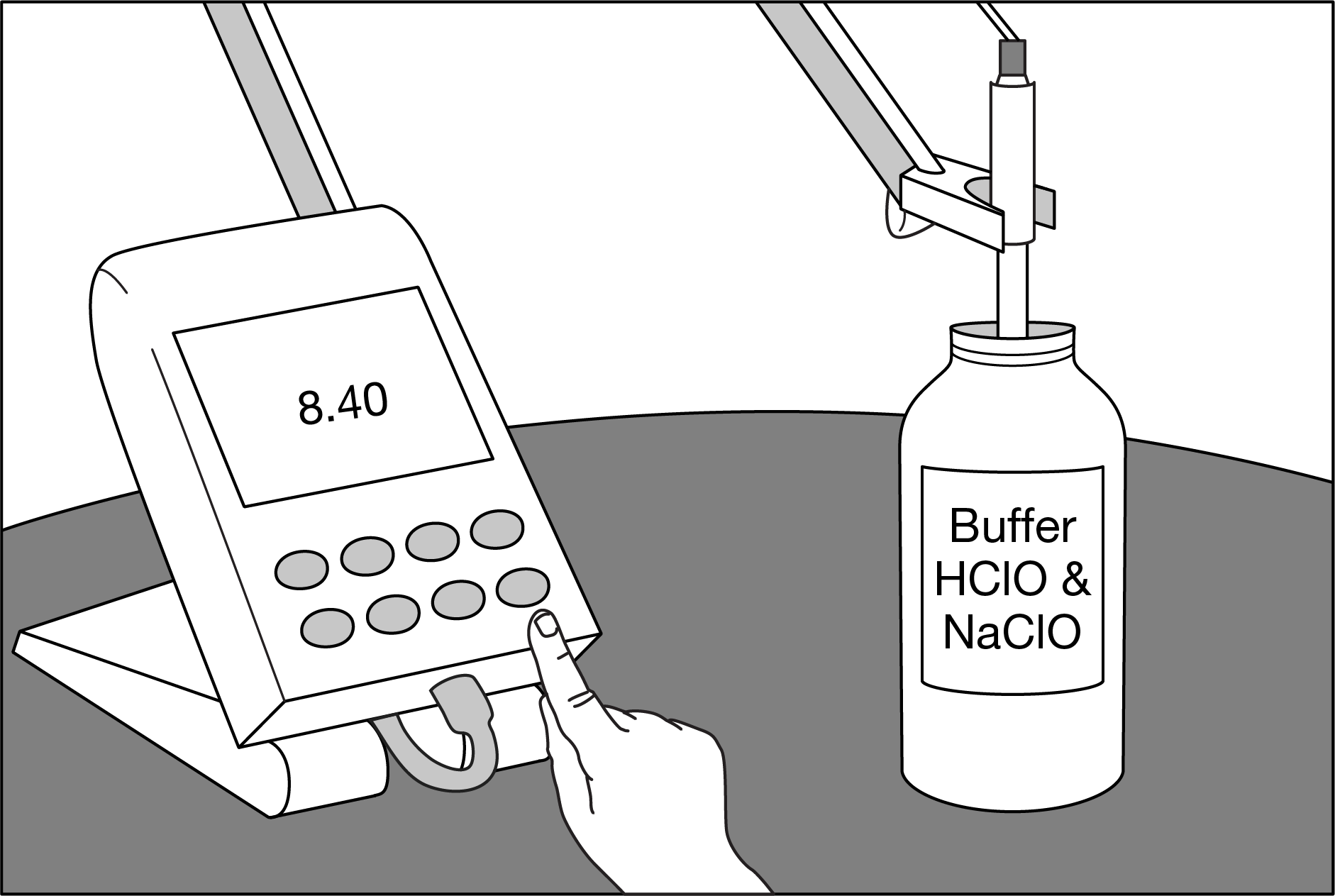
A student measures the pH of a 0.0100M buffer solution made with \(HClO\) and \(NaClO\), as shown above. The \(pK_a\) of \(HClO\) is 7.40 at 25°C. Based on this information, which of the following best compares the relative concentrations of \(ClO^−\) and \(HClO\) in the buffer solution?
A \([ClO^−]=[HClO]\)
B \( [ClO^−]>[HClO]\)
C \([ClO^−]<[HClO]\)
D It is not possible to compare the concentrations without knowing the \(pK_b\) of \(ClO^−\).
▶️Answer/Explanation
Ans:B
\( [ClO^−]>[HClO]\). When the \(pH>pK_a\), the base form has a higher concentration than the acid form.
Question
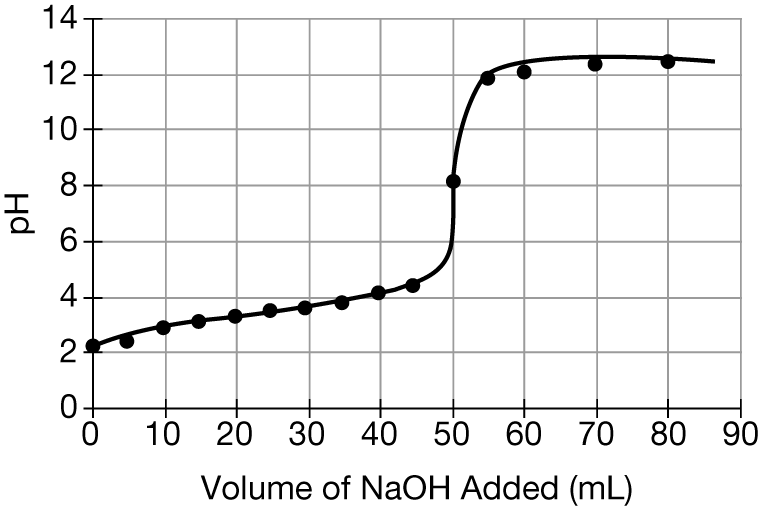
\(HCNO\) is a weak acid with a \(pK_a\) value of 3.5. The graph above shows the results of a titration of an aqueous solution of \(HCNO\) with 0.100M \(NaOH\). Based on the results, the concentration of \(CNO^−\) is greater than the concentration of \(HCNO\) at which of the following pH values?
A 2.0
B 3.0
C 3.5
D 4.0
▶️Answer/Explanation
Ans:D
When the \(pH>pK_a\), the base form has a higher concentration than the acid form. This is true at pH 4.0, which is greater than the \(pK_a\) value of 3.5.
Question
▶️Answer/Explanation
Ans:B
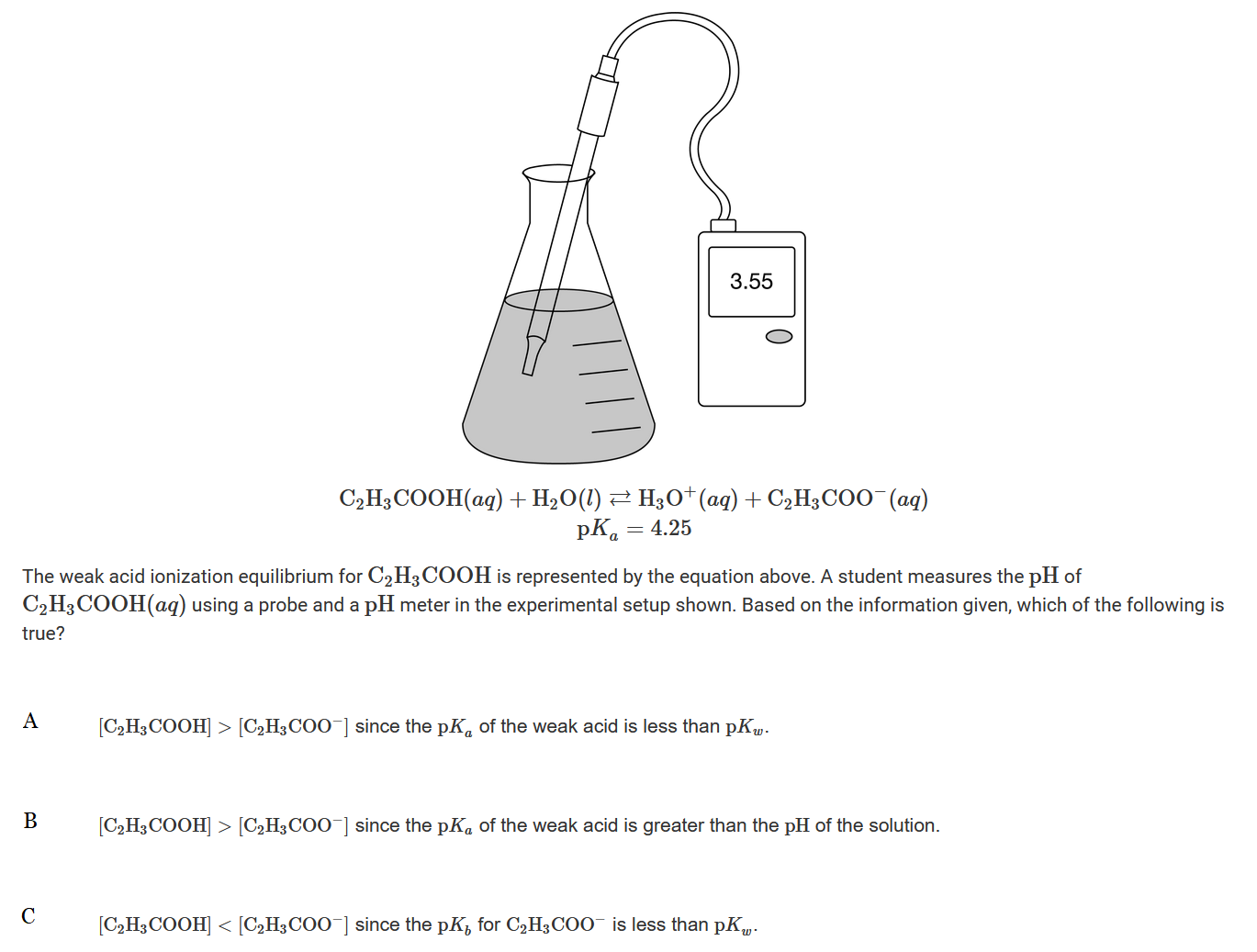
When \(pH<pK_a\) , the acid form, \(C_2H_3COOH\), has a higher concentration than the base form, \(C_2H_3COO^−\). This is true because 3.55<4.25.
Question
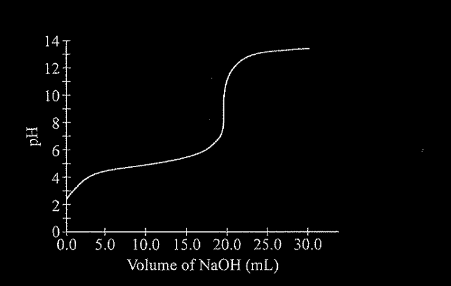
Data collected during the titration of a 20.0 mL sample of a 0.10 M solution of a monoprotic acid with a solution of NaOH of unknown concentration are plotted in the graph above. Based on the data, which of the following are the approximate pK of the acid and the molar concentration of the NaOH?
\(pK_{a}\) [NaOH]
(A) 4.7 0.050 M
(B) 4.7 0.10 M
(C) 9.3 0.050 M
(D) 9.3 0.10 M
▶️Answer/Explanation
Ans:B
Question
\(HN0_{2}(aq)\rightleftharpoons H^{+}N0_{2}^{-}(aq)\) \(K_{a}=4.0\times 10^{-4}\)
On the basis of the information above, what is the approximate percent ionization of \(HNO_{2}\) in a 1.0 M\( HNO_{2}\)(aq) solution?
(A) 0.00040%
(B) 0.020%
(C) 0.040%
(D) 2.0%
▶️Answer/Explanation
Ans:C