Questions

The process of dissolution of NaCl(s) in \(H_{2}O_{(l)}\) is represented in the diagram above. Which of the following summarizes the signs of \( \bigtriangleup H^{\circ }\) and \( \bigtriangleup S^{\circ }\) for each part of the dissolution process?

▶️Answer/Explanation
Ans: A
Breaking solvent-solvent interactions:
In the dissolution process, the water molecules (solvent) initially have strong hydrogen bonding interactions with each other. When a solute like NaCl is added, these solvent-solvent interactions need to be broken to accommodate the solute particles. Breaking these strong intermolecular forces is an endothermic process (\(\Delta H^\circ > 0\)), as energy needs to be absorbed to overcome the attractive forces. Additionally, breaking the ordered structure of water molecules leads to an increase in disorder or entropy (\(\Delta S^\circ > 0\)).
Breaking solute-solute interactions:
In the solid state, NaCl ions are held together by strong ionic bonds. When NaCl dissolves, these ionic bonds need to be broken, which requires energy input, making it an endothermic process (\(\Delta H^\circ > 0\)). Moreover, separating the ions from their ordered crystal lattice increases the disorder or entropy (\(\Delta S^\circ > 0\)).
Forming solute-solvent interactions:
After the solvent-solvent and solute-solute interactions are broken, the solute ions (\(Na^+\) and \(Cl^-\)) interact with the water molecules (solvent) to form new solute-solvent interactions. These new interactions involve ion-dipole attractions and hydrogen bonding, which are exothermic processes (\(\Delta H^\circ < 0\)), releasing energy. However, the formation of these interactions results in a more ordered system, decreasing the entropy (\(\Delta S^\circ < 0\)).
Therefore, option (A) correctly summarizes the signs of \(\Delta H^\circ\) and \(\Delta S^\circ\) for each part of the dissolution process, where both breaking solvent-solvent and solute-solute interactions are endothermic (\(\Delta H^\circ > 0\)) and increase entropy (\(\Delta S^\circ > 0\)), while forming solute-solvent interactions is exothermic (\(\Delta H^\circ < 0\)) and decreases entropy (\(\Delta S^\circ < 0\)).
Question

The chemical equation above represents the formation of \(SeF_6(g)\) from its elements, and the table provides the approximate values of S° for Se(s) and \(SeF_6(g)\). Based on the data, which of the following mathematical expressions can be used to correctly calculate S° for \(F_2(g)\) ?
A \(S^{\circ}=[−337+314−42]J/(mol⋅K)\)
B \(S^{\circ}=−[−337−314+42]J/(mol⋅K)\)
C \(S^{\circ}=\frac{1}{3}[−337+314−42]J/(mol⋅K)\)
D \(S^{\circ}=\frac{1}{3}[−337−314+42]J/(mol⋅K)\)
▶️Answer/Explanation
Ans:D
For the reaction ΔS°=−337J/(molrxn⋅K) , and ΔS°=Σ(moles of substance×S°)products−Σ(moles of substance×S°)reactants. If x=S° for \(F_2(g\)) then, \(−337J/(mol_{rxn}⋅K)=[314−(42+3x)]J/(mol⋅K)\). Solving for x,
S°\(=−13[−337−314+42]J/(mol⋅K)\) for \(F_2(g)\).
Question
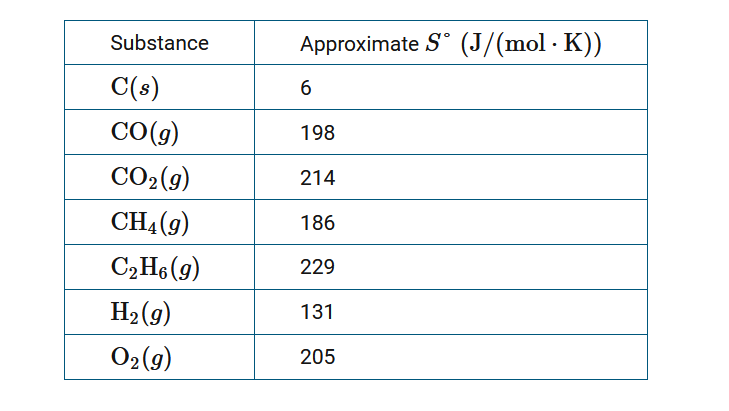
The table above provides approximate S° values for several substances. Based on the information, which of the following reactions has the largest increase in entropy, ΔS°?
A \(2C(s)+O_2(g)→2CO(g)\)
B \(C(s)+O_2(g)→CO_2(g)\)
C \(C(s)+2H_2(g)→CH_4(g)\)
D \(2C(s)+3H_2(g)→C_2H_6(g)\)
▶️Answer/Explanation
Ans:A
ΔS° for a reaction is calculated using ΔS°=Σ(moles of substance×S°)products−Σ(moles of substance×S°)reactants. Using the values given: for reaction A, ΔS°\(=[(2×198)−(2×6)−205]\) ; for reaction B, ΔS°\(=[214−6−205]\) ; for reaction C, \(ΔS°=[186−(2×131)−6]\); and for reaction D, \(ΔS°=[229−(2×6)−(3×131)]\). A quick look at the mathematical expressions shows that reaction A has the largest positive value of ΔS° and hence, the largest increase in entropy.
Question

The chemical equation above represents the combustion of glucose, and the table provides the approximate standard absolute entropies, S°, for some substances. Based on the information given, which of these equations can be used to calculate an approximate value of S° for \(H_2O(g)\)?
A \(S^{\circ}=[900+209+205−214]J/(mol⋅K)\)
B \(S^{\circ}=\frac{1}{6}[900+209+(6×205)−(6×214)]J/(mol⋅K)\)
C \(S^{\circ}=\frac{1}{6}[[−900−(6×214)+209+(6×205)]J/(mol⋅K)\)
D \(S^{\circ}=[−900−214+209+205]J/(mol⋅K)\)
▶️Answer/Explanation
Ans:B
The entropy change for the reaction is given by ΔS°\(_{rxn}\)=Σ(moles of substance×S°)\(_{products}\)−Σ(moles of substance×S°)\(_{reactants}\) . Using x to represent S° for \(H_2O(g)\),
\(900J/(mol_{rxn}⋅K)=(6×214)+6x−[209+(6×205)]J/(mol⋅K)\). Solving for x gives, x=S°\(=16[900+209+(6×205)−(6×214)]J/(mol⋅K)\).
Question
Which of the following equations represents a reaction for which the standard entropy change is positive \( \Delta S^{\circ}> 0\)?
(A)\(3O_{2}(g)\rightarrow 2O_{3}\)
(B)\(2H_{2}(g)+O_{2}\rightarrow 2H_{2}O\)(l)
(C)\(CaCO_{3}(s)\rightarrow CaO(s)+CO_{2}(g)\)
(D)\(I_{2}(g)+2K(s)\rightarrow 2Kl(s)\)
▶️Answer/Explanation
Ans:C
Question
\(C(diamond) \rightarrow C(graphite)\) \( \Delta G^{\circ}=-2.9KJ/MOL_{rxn}\)
Which of the following best explains why the reaction represented above is not observed to occur at room temperature?
(A) The rate of the reaction is extremely slow because of the relatively small value of\( \Delta G^{\circ}\) for the reaction.
(B) The entropy of the system decreases because the carbon atoms in graphite are less ordered than those in diamond.
(C) The reaction has an extremely large activation energy due to strong three-dimensional bonding among carbon atoms in diamond.
(D) The reaction does not occur because it is not thermodynamically favorable.
▶️Answer/Explanation
Ans:C