Question
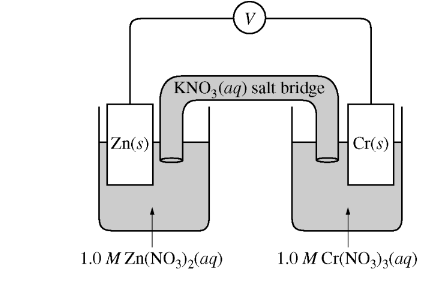
The standard reduction potentials for the half-reactions related to the galvanic cell represented above are listed in the table below.

Which of the following gives the value of\( E^ {\circ}_{cell}\)for the cell?
(A) \(E^ {\circ}_{cell}\)= −1.50 V
(B) \(E^ {\circ}_{cell}\)= −0.80 V
(C) \(E^ {\circ}_{cell}\)= −0.02 V
(D) \(E^ {\circ}_{cell}\) = +0.02 V
▶️Answer/Explanation
Ans:C
To find the standard cell potential ( \(\mathrm{E}^{\circ}\) cell) for the given galvanic cell, we need to use the reduction potentials provided in the table and apply the formula:
\(\mathrm{E}^{\circ}\) cell \(=\mathrm{E}^{\circ}\) cathode \(-\mathrm{E}^{\circ}\) anode
The cathode half-reaction is the reduction reaction with the more positive reduction potential, while the anode half-reaction is the reduction reaction with the less positive (or more negative) reduction potential.
In this case, the \(\mathrm{Zn}^{2+}(\mathrm{aq})+2 \mathrm{e}^{-} \rightarrow \mathrm{Zn}\) (s) half-reaction has a reduction potential of \(-0.76 \mathrm{~V}\), which is more positive than the \(\mathrm{Cr}^{3+}(\mathrm{aq})+3 \mathrm{e}^{-} \rightarrow \mathrm{Cr}(\mathrm{s})\) half-reaction with a reduction potential of \(-0.74 \mathrm{~V}\).
Therefore, the cathode half-reaction is:
\[
\mathrm{Zn}^{2+}(\mathrm{aq})+2 \mathrm{e}^{-} \rightarrow \mathrm{Zn}(\mathrm{s}) \quad \mathrm{E}^{\circ} \text { cathode }=-0.76 \mathrm{~V}
\]
And the anode half-reaction is:
\[
\mathrm{Cr}^{3+}(\mathrm{aq})+3 \mathrm{e}^{-} \rightarrow \mathrm{Cr}(\mathrm{s}) \quad \mathrm{E}^{\circ} \text { anode }=-0.74 \mathrm{~V}
\]
Substituting these values into the formula:
\[
\begin{aligned}
& \mathrm{E}^{\circ} \text { cell }=\mathrm{E}^{\circ} \text { cathode }-\mathrm{E}^{\circ} \text { anode } \\
& \mathrm{E}^{\circ} \text { cell }=-0.76 \mathrm{~V}-(-0.74 \mathrm{~V}) \\
& \mathrm{E}^{\circ} \text { cell }=-0.02 \mathrm{~V}
\end{aligned}
\]
So, the correct answer is (C) \(\mathrm{E}^{\circ} \mathrm{cell}=-0.02 \mathrm{~V}\).
Questions

Based on the information in the table above, which of the following shows the cell potential and the Gibbs free energy change for the overall reaction that occurs in a standard galvanic cell?
\(E_{cell}(V)\) \(\bigtriangleup G ^{\circ } (\frac{Kj}{mol_{rxn}})\)
(A) +1.63 -157
(B) +1.63 -944
(C) +5.63 -543
(D) +5.63 -3262
▶️Answer/Explanation
Ans: B
To find the cell potential (\(E_{\text{cell}}^{\circ}\)) and the Gibbs free energy change (\(\Delta G^{\circ}\)) for the overall reaction,use the given half-reactions and their standard reduction potentials (\(E^{\circ}\)).
The overall reaction is the sum of the two half-reactions:
- \( \mathrm{Mg}^{2+}(aq) + 2e^{-} \rightarrow \mathrm{Mg}(s) \) with \( E^{\circ} = -2.37 \) V
- \( \mathrm{Cr}^{3+}(aq) + 3e^{-} \rightarrow \mathrm{Cr}(s) \) with \( E^{\circ} = -0.74 \) V
balance the number of electrons transferred in each half-reaction.
- \( 3(\mathrm{Mg}^{2+}(aq) + 2e^{-} \rightarrow \mathrm{Mg}(s)) \)
This gives: \( 3\mathrm{Mg}^{2+}(aq) + 6e^{-} \rightarrow 3\mathrm{Mg}(s) \) - \( 2(\mathrm{Cr}^{3+}(aq) + 3e^{-} \rightarrow \mathrm{Cr}(s)) \)
This gives: \( 2\mathrm{Cr}^{3+}(aq) + 6e^{-} \rightarrow 2\mathrm{Cr}(s) \)
Adding these two balanced half-reactions together,
\[ 3\mathrm{Mg}^{2+}(aq) + 2\mathrm{Cr}^{3+}(aq) \rightarrow 3\mathrm{Mg}(s) + 2\mathrm{Cr}(s) \]
\[ E_{\text{cell}}^{\circ} = E_{\text{cathode}}^{\circ} – E_{\text{anode}}^{\circ} \]
the cathode (reduction) half-reaction is the reduction of chromium (\(\mathrm{Cr}^{3+}\)) and the anode (oxidation) half-reaction is the reduction of magnesium (\(\mathrm{Mg}^{2+}\)).
\[ E_{\text{cell}}^{\circ} = -(-0.74) – (-2.37) = 1.63 \text{ V} \]
\[ \Delta G^{\circ} = -nF E_{\text{cell}}^{\circ} \]
where \(n\) is the number of moles of electrons transferred in the balanced overall reaction, and \(F\) is the Faraday constant (\(96485 \text{ C/mol}\)).
In the given reaction, 6 moles of electrons are transferred.
\[ \Delta G^{\circ} = -6 \times 96485 \text{ C/mol} \times 1.63 \text{ V} = -944 \text{ kJ/mol} \]
Therefore, the correct answer is option (B):
\[
(B) \quad +1.63 \text{ V} \quad \text{and} \quad -944 \text{ kJ/mol}
\]
Question
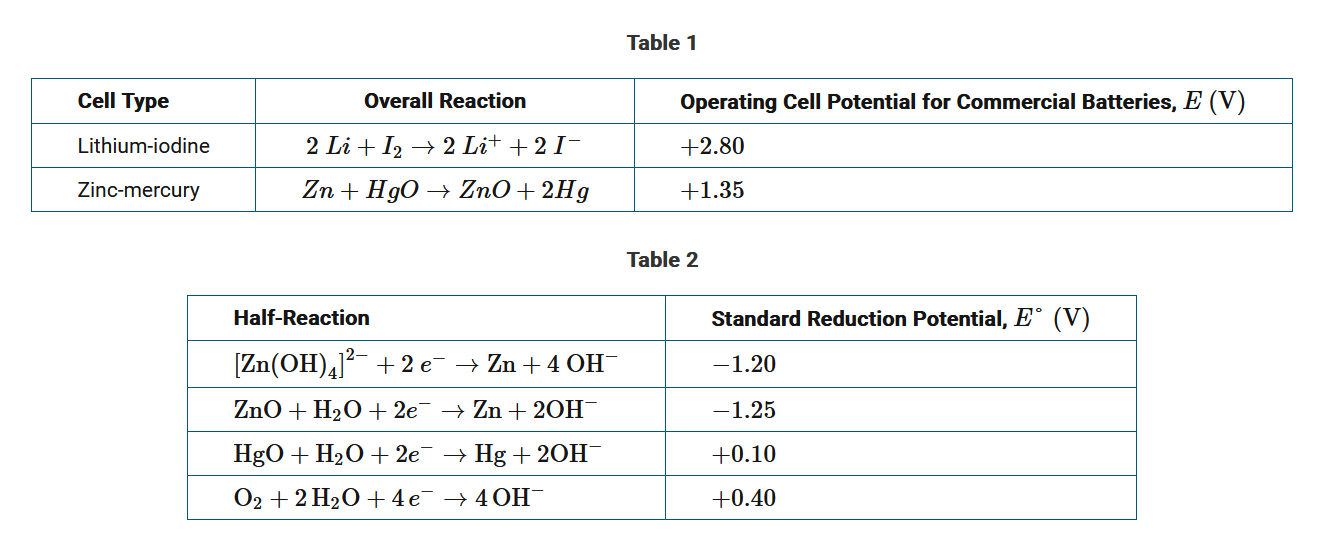
Pacemakers are electronic devices that help regulate the heart rate. Currently, lithium-iodine cells are commonly used to power pacemakers and have replaced zinc-mercury cells. Table 1 provides the operating cell potential, E , for each cell. Table 2 provides the standard reduction potentials for several half-reactions related to zinc-mercury and zinc-air cells.
The use of zinc-mercury cells in hearing aids has been replaced by zinc-air cells that operate using the oxidation of Zn by \(O_2\) from the air, generating a potential of +1.60V . Table 2 provides the standard reduction potentials for the half-reactions used in zinc-mercury and zinc-air cells. Which of the following best explains the modification to the cell design that is mostly responsible for the difference in standard cell potentials for zinc-mercury and zinc-air cells?
A The greater standard cell potential of the Zn-air cell compared to that of the zinc-mercury cell most likely results from the thermodynamically more favorable reduction of \(O_2\) compared to \(HgO\).
B The greater standard cell potential of the Zn-air cell compared to that of the zinc-mercury cell most likely results from the greater number of moles of \(e^−\) required to reduce \(O_2\) compared to \(HgO\).
C The greater standard cell potential of the Zn-air cell compared to that of the zinc-mercury cell most likely results from the thermodynamically less favorable reduction of \(O_2\) compared to \(HgO\).
D The greater standard cell potential of the Zn-aircell compared to that of the zinc-mercury cell most likely results from the greater number of moles of hydroxide ions required to reduce \([Zn(OH)_4]^{2−}\) compared to \(Zn(OH)_2\).
▶️Answer/Explanation
Ans:A
Based on the information in table 2 and the cell potential given, the reaction that takes place in the zinc-air cell is \(2Zn+4 OH^−+O^2+2 H_2O→2[Zn(OH)_4]^{2−}\). The relatively small difference in the standard reduction potential for Zn(OH)2 compared to that for [Zn(OH)4]2− indicates that the oxidation of zinc under both of these conditions cannot account for the difference in E°cell between the zinc-mercury and zinc-air cells. Therefore, the larger, more positive standard reduction potential for \(O_2\) compared to that for \(HgO\) is mostly responsible for the difference in cell potentials. This is justified by ΔG\(=−nFE\) because a larger, more positive E° results in a larger, more negative ΔG and a reaction that is thermodynamically more favorable.
Question
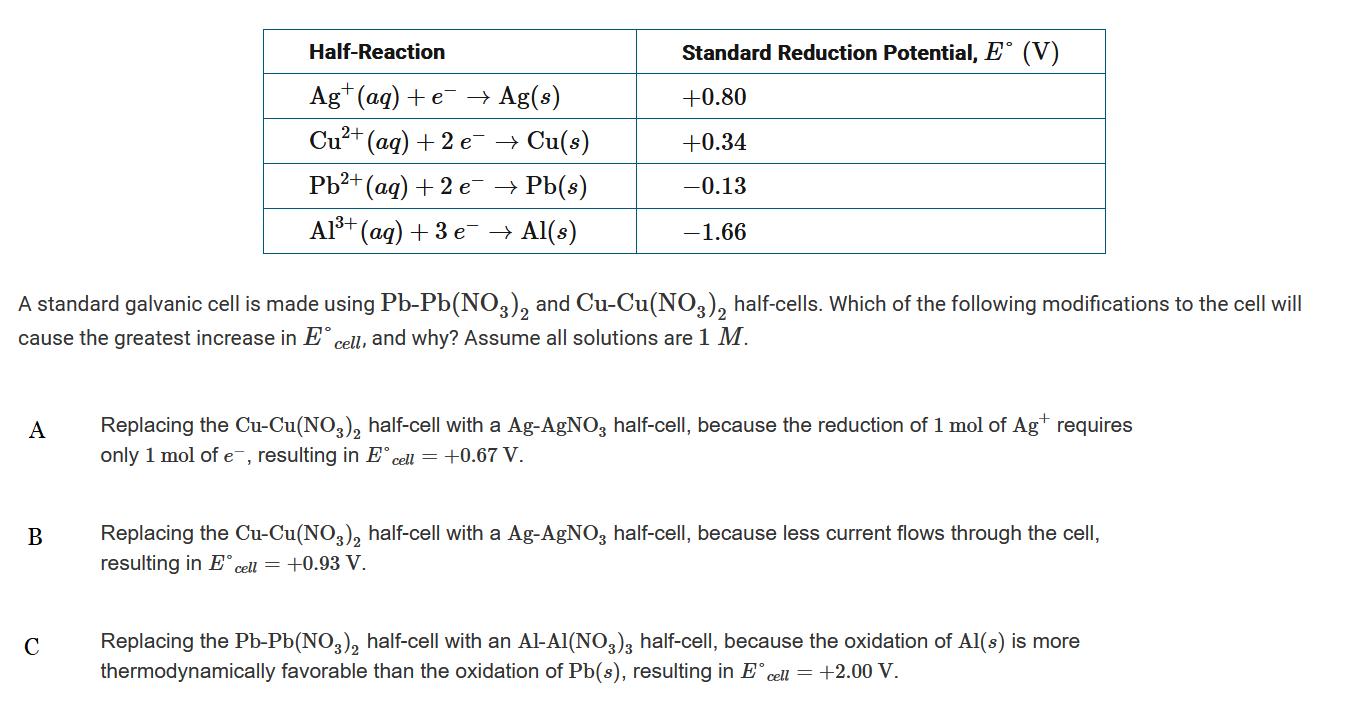
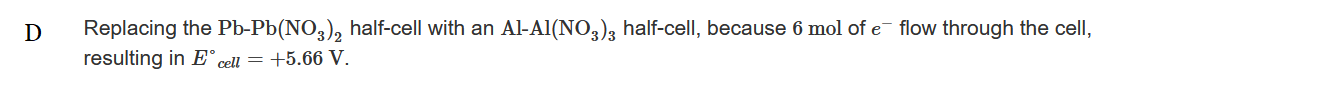
▶️Answer/Explanation
Ans:C
Replacing the \(Pb-Pb(NO_3)_2\) half-cell with an \(Al-Al(NO_3)_3\) half-cell, not the \(Cu-Cu(NO_3)_2\) half-cell with a \(Ag-AgNO_3\) half-cell, causes the greatest increase in E°cell. The replacement means that the reaction taking place is \(2Al(s)+3Cu_^{2+}(aq)→2Al_3+(aq)+3Cu(s)\), and \(E^{\circ}_{cell}=+2.00V\).
Question
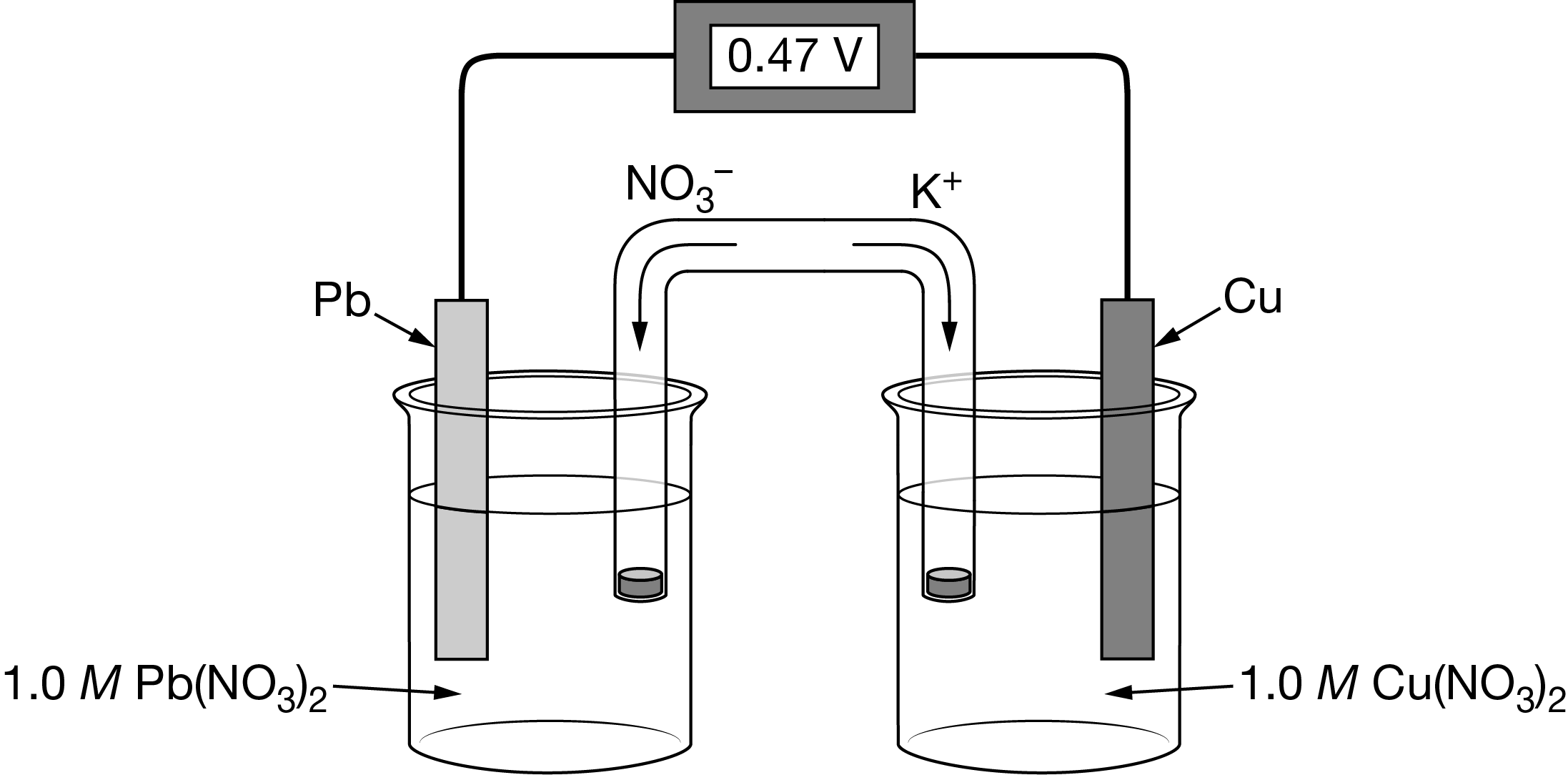
The galvanic cell illustrated above was constructed using a salt bridge containing \(KNO_3\). A second cell is constructed from identical half-cells but uses \(NaNO_3\) for the salt bridge. Which of the following best explains whether the initial potential of the second cell will be different from the initial potential of the first cell?
A The initial potential of the second cell will be lower than the initial potential of the first cell because Na has a lower molar mass than K has.
B The initial potential of the second cell will be higher than the initial potential of the first cell because Na is less electronegative than K is.
C The initial potential of the second cell will be the same as the first cell because the ions from the salt bridge are not oxidized or reduced during cell operation.
D The initial potential of the second cell will be the same as the first cell because the standard reduction potentials of Group 1 metals are very similar.
▶️Answer/Explanation
Ans:C
Based on the movement of ions in the salt bridge shown in the illustration provided for the first cell, the redox reaction that takes place is \(Cu_2^+(aq)+Pb(s)→Cu(s)+Pb_2^+(aq)\) . The ions from the salt bridge are not part of the redox process that generates the cell potential, and as a result, the initial E° for the two cells will be the same.
Question
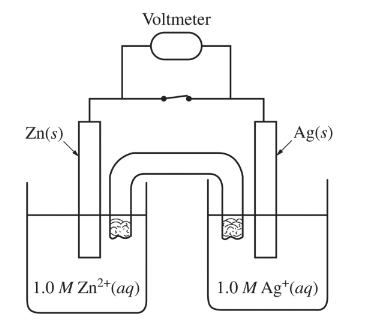
Standard reduction potentials for the half-reactions associated with the electrochemical cell shown above are given in the table below.

What is the value of E° for the cell?
(A) 0.04 V
(B) 0.84 V
(C) 1.56 V
(D) 2.36 V
▶️Answer/Explanation
Ans:C