Electric Charges and Fields : Notes and Study Materials -pdf
CBSE Class 12 Physics, Chapter 1: Electric Charges and Fields. These notes are very useful for revision purposes before the exam.
The complete chapter is divided into several parts and this is the Part – I.
Electrostatics
Electrostatics deals with the study of forces, fields and potentials arising from static charges. The name electricity is coined from the Greek word elektron meaning amber.
Important facts about Electric Charges
The name electricity is coined from the Greek word elektron meaning amber.
There are two kinds of charges.
By convention, the charge on electron is considered as negative & the charge on proton is considered as positive.
If we say that a body is charged, it means body have excess or deficit of electrons.
A body having negative charge implies that body has excess of electrons. A body having positive charge implies that body is deficient of electrons.
In solids, some of the electrons, being less tightly bound in the atom, are the charges which are transferred from one body to the other. A body can thus be charged positively by losing some of its electrons. Similarly, a body can be charged negatively by gaining electrons.
The SI unit of electric charge is coulomb. The c.g.s. unit of charge is stat coulomb.
Gold – Leaf Electroscope
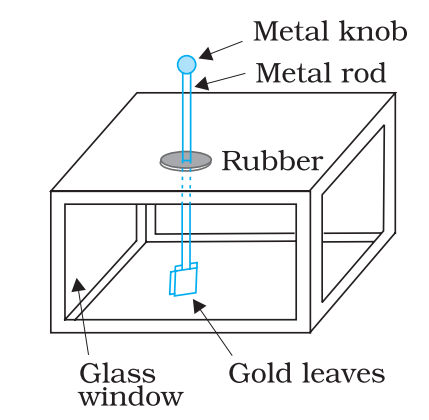
It is a device used to detect the nature and amount of electric charge present in a charged body.
It consists of a vertical metal rod housed in a box, with two thin gold leaves attached to its bottom end. When a charged object touches the metal knob at the top of the rod, charge flows on to the leaves and they diverge. The degree of divergance is an indicator of the amount of charge.
Basic Properties of Electric Charges
Additivity of Charges:
If a system contains two point charges q1 and q2, the total charge of the system is obtained simply by adding algebraically q1 and q2 , i.e., charges add up like real numbers or they are scalars like the mass of a body.
If a system contains n charges q1, q2, q3, …, qn, then the total charge of the system is q1 + q2 + q3 + … + qn.
Charge is conserved:
Within an isolated system consisting of many charged bodies, due to interactions among the bodies, charges may get redistributed but it is found that the total charge of the isolated system is always conserved.
Quantisation of charge
Experimentally it is established that all free charges are integral multiples of a basic unit of charge denoted by e. Thus charge q on a body is always given by q = n e, here n is any integer, positive or negative. This basic unit of charge is the charge that an electron or proton carries. By convention, the charge on an electron is taken to be negative; therefore charge on an electron is written as –e and that on a proton as +e. (e = 1.602192 × 10–19 C)
Methods of Charging
A body can be charged by friction, induction and conduction.
Charging by Friction:
When certain insulators are rubbed with cloth or fur, they become electrically charged due to the transfer or charge or electrons. As the two objects are rubbed together, one object loses electrons while the other gains electrons.
There is a transfer of electrons from one object to the other. The object that gains electrons becomes negatively charged, while the object that loses electrons has an excess of positive charge. Hence it is positively charged. The transfer of charge is due to the contact between the materials, and the amount of charge transferred depends on the nature of these materials.
Charging by Induction:
Induction is the process by which a uncharged body is charged by using a charged body without actual contact between them or losing its own
charge.
If a charged body is brought near a neutral body, the charged body attracts opposite charge and repels similar charge present on the
neutral body.
Afterwards, the neutral body is earthed and the like charge is neutralised by the flow of charge from earth leaving unlike charge on
the body. Now the earthing and the charging body are removed leaving the initially neutral body charged.
Charging by Conduction:
In the process of charging by conduction, direct contact of charged and uncharged body is involved and both objects acquire the same kind of charge. If a negative object is used to charge a neutral object, then both objects become charged negatively and vice versa.
Coulomb’s law
According to this law “The magnitude of the electric force between two static point charges, in vacuum, is directly proportional to the product of the magnitude of the two charges and inversely proportional to the square of the distance between them and acts along the straight line joining the two charges”.
The magnitude of Coulomb’s law is given by the expression:
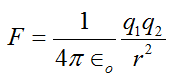
Where, F is the force between two point charges, q1 and q2 are magnitude of charges, r is the distance between these charges.
Some facts about Coulomb’s law:
• Coulomb’s law should be used for point charges in vacuum at rest. It is not valid for charges in motion.
• The electrostatics force acts along the line joining the two charges. It obeys Newton’s third law of motion.
• Coulomb’s force is not affected by the presence of other charges in the neighborhood; hence, the principle of superposition is valid.
• Force between like charges is repulsive and between unlike charges attractive.
Coulomb’s law in vector form:
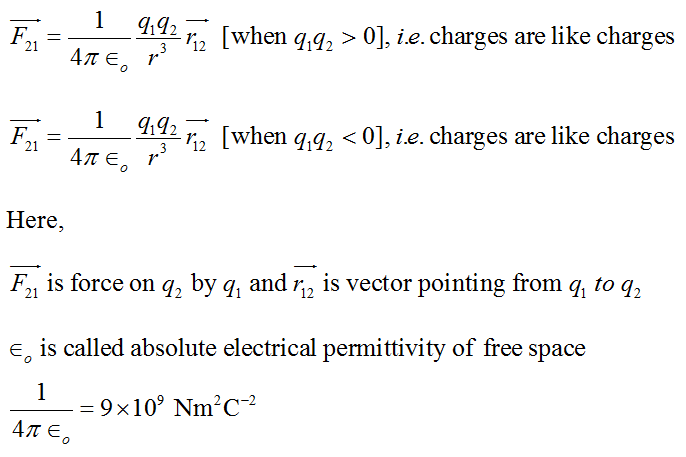
Superposition Principle:
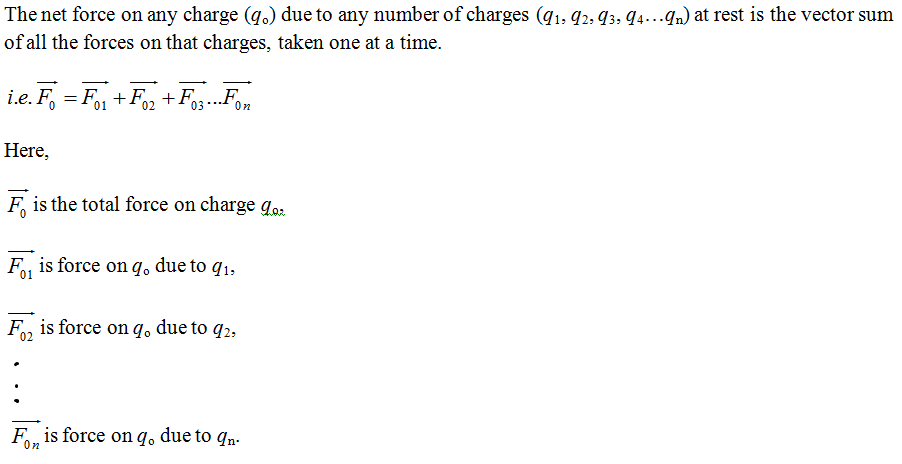
Electric Field:
Electric field due to a given charge is the space around the charge in which electrostatic force of attraction or repulsion due to the charge can be experienced by any other charge.
Source Charge & Test Charge:
The charge which produces electric field is known as source charge.
Charge (generally written as qo) which tests the effect of source charge is called test charge.
Electric Field Intensity:
Electric filed intensity at any point is the strength of electric field at that point. It is defined as the force experienced by unit positive charge placed at that point.
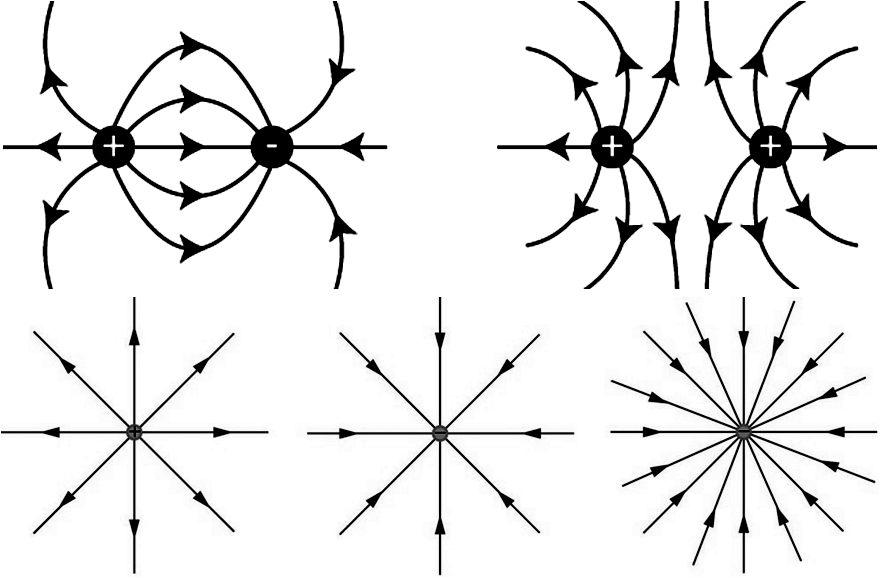
Electric Field Line:
An electric field line is defined as a path, straight or curved in electric field, such that tangent to it at any point gives the direction of electric field intensity at that point
Properties of Electric Field Lines:
• Electric field lines are continuous curves.
• They start from positively charge and end at negatively charges body
• Tangent to the electric filed line at any point gives the direction of electric field intensity at that point
• No two electric field lines intersect each other
• Electric field lines are always normal to the surface of of a conductor
Expression for electric field intensity at a point:
Electric field intensity due to a point charge:
Electric field intensity at any point due to a group of point charges:
Electric field intensity at any point due to a group of point charges is equal to the vector sum of electric field intensities due to individual charges at the same point.
Electric Dipole:
An electric dipole consists of a pair of equal and opposite point charges separated by some small distance.
Dipole Moment:
It is a measure of the strength of electric dipole. The magnitude of dipole moment is given by product of either charge and the distance between them.
It is a vector quantity whose direction is from negative to positive charge.
CBSE Class 12 Physics Important Questions Chapter 1 – Electric Charges and Fields
1 Mark Questions
1. Show does the force between two point charges change if the dielectric constant of the medium in which they are kept increase?
Ans. Since K
= 
if k increases, Fm decreases.
2. A charged rod P attracts rod R where as P repels another charged rod Q. What type of force is developed between Q and R?
Ans. Suppose rod P be negatively charged since it attracts rod R
R is positively charged since it repels rod Q Q is negatively charged. So force between Q and R is attractive in nature.
3. Which physical quantity has its S.I unit (1) Cm (2) N/C
Ans. (1) Electric dipole moment (2) Electric field Intensity
4. Define one coulomb?
Ans. Charge on a body is said to be 1 coulomb if two charges experiences a force of repulsion or attraction of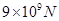 
when they are separated by a distance of 1 m.
2 Mark Questions
1. A free proton and a free electron are placed in a uniform field. Which of the two experience greater force and greater acceleration?
Ans. As F = q E and a = F/m as charge on both e-1 and proton are equal and opposite in nature, so force on them would be equal but as mass of proton is more than that of electron, so acceleration of electron would be more.
2. No two electric lines of force can intersect each other? Why?
Ans. Two electric lines of force never intersect each other because if they intersect then at the point of intersection there will be two tangents which is not possible as the two tangents represents two directions for electric field lines.
3. The graph shows the variation of voltage V across the plates of two capacitors A and B versus increase of charge Q stored on them. Which of the two capacitors have higher capacitance? Give reason for your answer?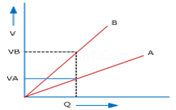
Ans. Since C=Q/V
For a given charge Q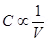
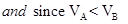
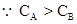
4. An electric dipole when held at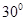 
with respect to a uniform electric field of 
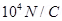experienced a Torque of 
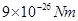. Calculate dipole moment of the dipole?
Ans. Given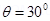
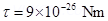
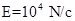
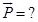
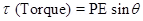
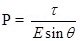
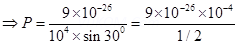
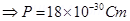
5. (a) Explain the meaning of the statement ‘electric charge of a body is quantised’.
(b) Why can one ignore quantisation of electric charge when dealing with macroscopic i.e., large scale charges?
Ans. (a) Electric charge of a body is quantized. This means that only integral (1, 2, …., n) number of electrons can be transferred from one body to the other. Charges are not transferred in fraction. Hence, a body possesses total charge only in integral multiples of electric charge.
(b) In macroscopic or large scale charges, the charges used are huge as compared to the magnitude of electric charge. Hence, quantization of electric charge is of no use on macroscopic scale. Therefore, it is ignored and it is considered that electric charge is continuous.
6. When a glass rod is rubbed with a silk cloth, charges appear on both. A similar phenomenon is observed with many other pairs of bodies. Explain how this observation is consistent with the law of conservation of charge.
Ans. Rubbing produces charges of equal magnitude but of opposite nature on the two bodies because charges are created in pairs. This phenomenon of charging is called charging by friction. The net charge on the system of two rubbed bodies is zero. This is because equal amount of opposite charges annihilates each other. When a glass rod is rubbed with a silk cloth, opposite natured charges appear on both the bodies. This phenomenon is in consistence with the law of conservation of energy. A similar phenomenon is observed with many other pairs of bodies.
7. (a) An electrostatic field line is a continuous curve. That is, a field line cannot have sudden breaks. Why not?
(b) Explain why two field lines never cross each other at any point?
Ans. (a) An electrostatic field line is a continuous curve because a charge experiences a continuous force when traced in an electrostatic field. The field line cannot have sudden breaks because the charge moves continuously and does not jump from one point to the other.
(b) If two field lines cross each other at a point, then electric field intensity will show two directions at that point. This is not possible. Hence, two field lines never cross each other.
8. An electric dipole with dipole moment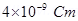 
is aligned at 
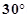with the direction of a uniform electric field of magnitude 
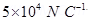Calculate the magnitude of the torque acting on the dipole.
Ans. Electric dipole moment, 
Angle made by p with a uniform electric field,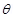 
=
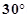
Electric field,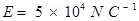 
Torque acting on the dipole is given by the relation,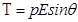
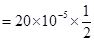
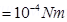
Therefore, the magnitude of the torque acting on the dipole is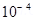 
N m.
9. Figure 1.33 shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?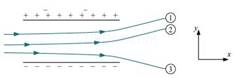
Ans. Opposite charges attract each other and same charges repel each other. It can be observed that particles 1 and 2 both move towards the positively charged plate and repel away from the negatively charged plate. Hence, these two particles are negatively charged. It can also be observed that particle 3 moves towards the negatively charged plate and repels away from the positively charged plate. Hence, particle 3 is positively charged.
The charge to mass ratio (emf) is directly proportional to the displacement or amount of deflection for a given velocity. Since the deflection of particle 3 is the maximum, it has the highest charge to mass ratio.
10. What is the net flux of the uniform electric field of Exercise 1.15 through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?
Ans. All the faces of a cube are parallel to the coordinate axes. Therefore, the number of field lines entering the cube is equal to the number of field lines piercing out of the cube. As a result, net flux through the cube is zero.
11. Careful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is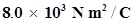 
. (a) What is the net charge inside the box? (b) If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box? Why or Why not?
Ans. (a) Net outward flux through the surface of the box,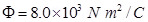 
For a body containing net charge q, flux is given by the relation,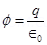
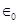= Permittivity of free space
q = ∈0Φ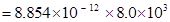
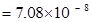
= 0.07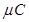 
Therefore, the net charge inside the box is 0.07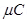
.
(b) No
Net flux piercing out through a body depends on the net charge contained in the body. If net flux is zero, then it can be inferred that net charge inside the body is zero. The body may have equal amount of positive and negative charges.
3 Mark Questions
1. A particle of mass m and charge q is released form rest in a uniform electric field of intensity E. calculate the kinetic energy it attains after moving a distances between the plates?
Ans. Since F = qE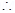
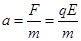—1
Using third equation of motion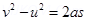
Initially charged particle is at rest 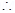u = o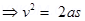
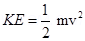
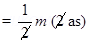
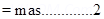
Substituting 1 in eq. 2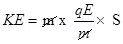
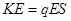
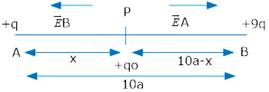
2. Two point charges +q and +9q are separated by a distance of 10 a. Find the point on the line joining the two changes where electric field is zero?
Ans. Let P be the pt where test charge (+qo) is present then electric field at pt. P will be zero if Field at pt. P due to +q = field at p+. P due to + 9q————1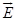
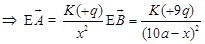
Substituting in eq. 1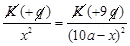
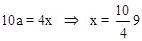
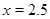a from change (+q)
Or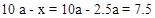
a from change (+9q)
3. Define the term dipole moment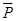 
of an electric dipole indicating its direction. Write its S.I unit. An electric dipole is placed in a uniform electric field 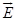. Deduce the expression for the Torque acting on it.
Ans. Electric dipole moment is defined as the product of the magnitude of either charge and the length of dipole. Its direction is from –ve to +ve charge.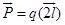
Its S.I. unit is coulomb meter (Cm)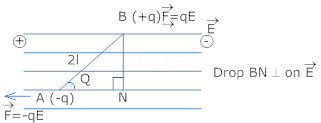
Consider a dipole placed in uniform electric field and makes an angle (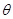
) with the electric field 
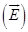Since two forces acts on the charges constituting an electric dipole which are equal and opposite in direction, thus a torque acts on the dipole which makes the dipole rotate.
And Torque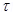 
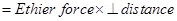
Here force (F) = qE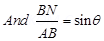
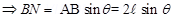
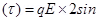
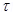() = PE Sin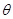 
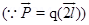
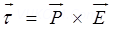
In vector form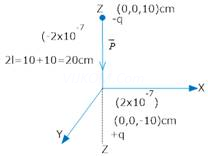
4. A sphere of radius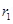 
encloses a change Q. If there is another concentric sphere 
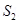of radius 
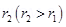and there is no additional change between 
. Find the ratio of electric flux through ?
Ans. 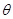= q/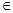
o (where 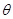=electric flux)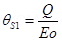
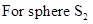
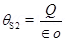
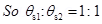
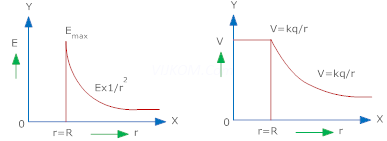
5. Electric charge is uniformly distributed on the surface of a spherical balloon. Show how electric intensity and electric potential vary (a) on the surface (b) inside and (c) outside.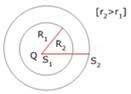
Ans. Electric field intensity on the surface of a shell
E =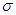 
/
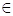o& V = Kq/R
Inside E = o& V = Kq/R
Outside E =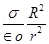 
& V = Kq/r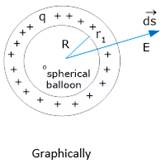
6. Two point electric charges of value q and 2q are kept at a distance d apart from each other in air. A third charge Q is to be kept along the same line in such a way that the net force acting on q and 2q is zero. Calculate the position of charge Q in terms of q and d.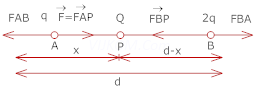
Ans. Net force on charge q and 2q will be zero if the third charge is negative (i.e. of opposite sign) and q and 2q are positive, Force on change q will be zero if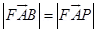
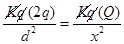
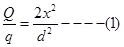
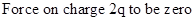
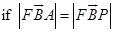
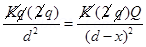
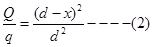
comparing equation 1 and 2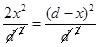
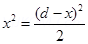
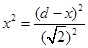
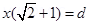
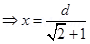
7. What is the force between two small charged spheres having charges of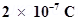 
and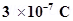 
placed 30 cm apart in air?
Ans.Repulsive force of magnitude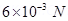 
Charge on the first sphere,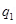 
= 
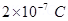
Charge on the second sphere,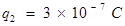 
Distance between the spheres, r = 30 cm = 0.3 m
Electrostatic force between the spheres is given by the relation,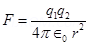
Where,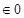 
= Permittivity of free space
s
Hence, force between the two small charged spheres is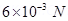. The charges are of same nature. Hence, force between them will be repulsive.
8. The electrostatic force on a small sphere of charge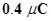 
due to another small sphere of charge – 
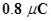in air is 
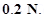(a) What is the distance between the two spheres? (b) What is the force on the second sphere due to the first?
Ans. (a) Electrostatic force on the first sphere, F =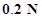 
Charge on this sphere,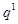 
= 
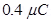
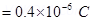
Charge on the second sphere,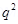 
= – 
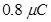
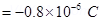
Electrostatic force between the spheres is given by the relation,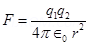 
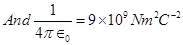
Where,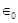 
= Permittivity of free space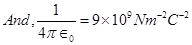
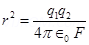
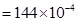
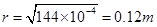
The distance between the two spheres is 0.12m.
(b) Both the spheres attract each other with the same force. Therefore, the force on the second sphere due to the first is 0.2N.
9. A polythene piece rubbed with wool is found to have a negative charge of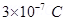 
(a) Estimate the number of electrons transferred (from which to which?)
(b) Is there a transfer of mass from wool to polythene?
Ans. (a) When polythene is rubbed against wool, a number of electrons get transferred from wool to polythene. Hence, wool becomes positively charged and polythene becomes negatively charged.
Amount of charge on the polythene piece,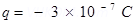 
Amount of charge on an electron,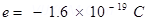 
Number of electrons transferred from wool to polythene = n
n can be calculated using the relation,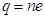
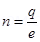
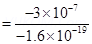
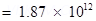
Therefore, the number of electrons transferred from wool to polythene is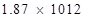
.
(b) Yes.
There is a transfer of mass taking place. This is because an electron has mass,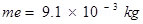
Total mass transferred to polythene from wool,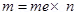
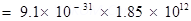
Hence, a negligible amount of mass is transferred from wool to polythene.
10.Consider a uniform electric field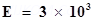 
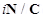. (a) What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane? (b) What is the flux through the same square if the normal to its plane makes a 
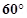angle with the x-axis?
Ans. (a) Electric field intensity,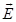 
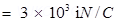
Magnitude of electric field intensity,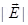 
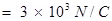
Side of the square, s = 10 cm = 0.1 m
Area of the square, 
The plane of the square is parallel to the y-z plane. Hence, angle between the unit vector normal to the plane and electric field,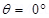 
Flux (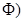
through the plane is given by the relation,
= 
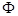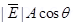
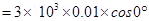
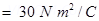
(b) Plane makes an angle of 60° with the x-axis. Hence, θ = 60°
Flux, =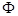 
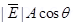
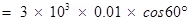
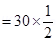
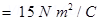
11. A point charge +10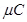 
is a distance 5 cm directly above the centre of a square of side 10 cm, as shown in Fig. 1.34. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with edge 10 cm.)
Ans. The square can be considered as one face of a cube of edge 10 cm with a centre where charge q is placed. According to Gauss’s theorem for a cube, total electric flux is through all its six faces.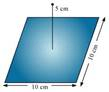
Hence, electric flux through one face of the cube i.e., through the square,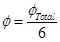 
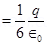
Where,
∈0 = Permittivity of free space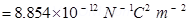
q = 10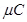
∴
= 
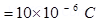
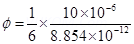
Therefore, electric flux through the square is 1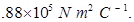
12. A point charge of 2.0 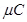is at the centre of a cubic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface?
Ans. Net electric flux (ΦNet) through the cubic surface is given by,
ϕNet=qϵ0
Where, ∈0 = Permittivity of free space
= 8.854 × 10−12 N−1C2 m−2
q = Net charge contained inside the cube = 2.0 μC = 2 × 10−6 C
∴ ϕNet=2×10−68.854×10−12
= 2.26 × 105 N m2 C−1
The net electric flux through the surface is 2.26 ×105 N m2C−1.
13. A point charge causes an electric flux of –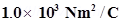 
to pass through a spherical Gaussian surface of 10.0 cm radius centered on the charge. (a) If the radius of the Gaussian surface were doubled, how much flux would pass through the surface? (b) What is the value of the point charge?
Ans. (a) Electric flux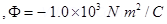
Radius of the Gaussian surface,
r = 10.0 cm
Electric flux piercing out through a surface depends on the net charge enclosed inside a body. It does not depend on the size of the body. If the radius of the Gaussian surface is doubled, then the flux passing through the surface remains the same i.e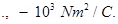
(b) Electric flux is given by the relation,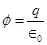
Where,
q = Net charge enclosed by the spherical surface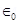
= Permittivity of free space =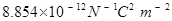 
∴
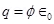
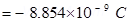
= – 8.854 nC
Therefore, the value of the point charge is –8.854 nC.
14. A conducting sphere of radius 10 cm has an unknown charge. If the electric field 20 cm from the centre of the sphere is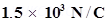 
and points radially inward, what is the net charge on the sphere?
Ans. Electric field intensity (E) at a distance (d) from the centre of a sphere containing net charge q is given by the relation,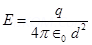
Where,
q = Net charge =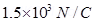 
d = Distance from the centre = 20 cm = 0.2 m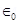 = Permittivity of free space
And,
= 9 × 109 N 
C – 2
∴
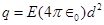
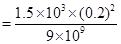
= 6.67 nC
Therefore, the net charge on the sphere is 6.67 nC.
15. A uniformly charged conducting sphere of 2.4 m diameter has a surface charge density of 80.0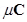 
/m2. (a) Find the charge on the sphere. (b) What is the total electric flux leaving the surface of the sphere?
Ans. (a) Diameter of the sphere, d = 2.4 m
Radius of the sphere, r = 1.2 m
Surface charge density, 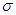= 80.0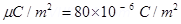 
Total charge on the surface of the sphere,
Q = Charge density × Surface area
=
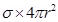
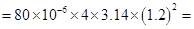
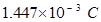
Therefore, the charge on the sphere is 
(b) Total electric flux (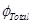
) leaving out the surface of a sphere containing net charge Q is given by the relation,
Where,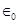
= Permittivity of free space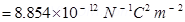
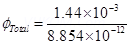
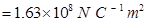
Therefore, the total electric flux leaving the surface of the sphere is 
16. An infinite line charge produces a field of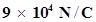 
at a distance of 2 cm. Calculate the linear charge density.
Ans. Electric field produced by the infinite line charges at a distance d having linear charge density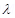 
is given by the relation,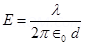
Where,
d = 2 cm = 0.02 m
E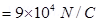 
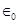= Permittivity of free space= 
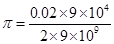
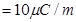
Therefore, the linear charge density is .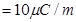
17. Which among the curves shown in Fig. 1.35 cannot possibly represent electrostatic field lines?
(a)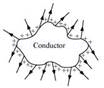 
(b)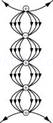 
(c)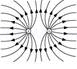 
(d)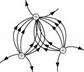 
(e)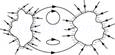 
Ans. (a) The field lines showed in (a) do not represent electrostatic field lines because field lines must be normal to the surface of the conductor.
(b) The field lines showed in (b) do not represent electrostatic field lines because the field lines cannot emerge from a negative charge and cannot terminate at a positive charge.
(c) The field lines showed in (c) represent electrostatic field lines. This is because the field lines emerge from the positive charges and repel each other.
(d) The field lines showed in (d) do not represent electrostatic field lines because the field lines should not intersect each other.
(e) The field lines showed in (e) do not represent electrostatic field lines because closed loops are not formed in the area between the field lines.
18. Suppose that the particle in Exercise in 1.33 is an electron projected with velocity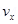 
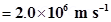. If E between the plates separated by 0.5 cm is 
, where will the electron strike the upper plate? (| e | = 
.)
Ans. Velocity of the particle,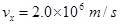 
Separation of the two plates, d = 0.5 cm = 0.005 m
Electric field between the two plates, E 
Charge on an electron, q =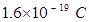 
Mass of an electron, me =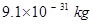 
Let the electron strike the upper plate at the end of plate L, when deflection is s.
Therefore,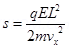
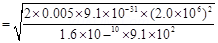
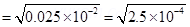
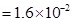
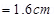
Therefore, the electron will strike the upper plate after travelling 1.6 cm.
5 Mark Questions
1. (1) The electric field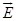 
due to a point change at any point near to it is defined as:
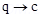where q is the test charge and 
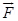is the force acting on it. What is the significance of lim 
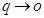in this expression?
(2) Two charges each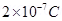 
but opposite in sign forms a system. These charges are located at points A (0,0, -10) cm and B (0,0, +10) cm respectively. What is the total charge and electric dipole moment of the system?
Ans. (1) The Significance of writing lim 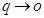means the test charge should be vanishingly small so that it should not disturb the presence of source charge.
(2) 
(i) Total charge of the system
= 
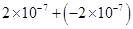
= zero. 
(ii)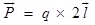 
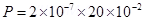
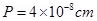
Direction of Dipole moment -Along negative z-axis.
2. (a) Sketch electric lines of force due to (i) isolated positive change (ie q>0) and (ii) isolated negative change (ie q<0)
(b) Two point changes q and –q are placed at a distance 2a apart. Calculate the electric field at a point P situated at a distance r along the perpendicular bisector of the line joining the charges. What is the field when r >> a?
Ans.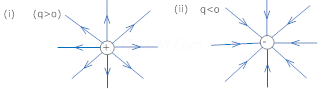
(b)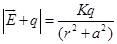
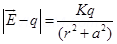
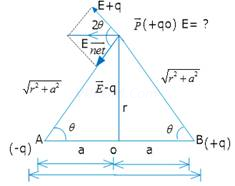
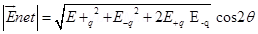
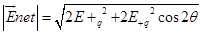
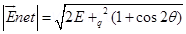
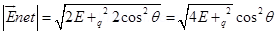
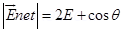
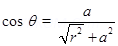
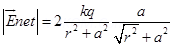
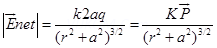
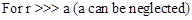
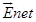can be calculated by using a parallelogram law of vector addition.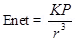 
3. (a) What is an equi-potential surface? Show that the electric field is always directed perpendicular to an equi-potential surface.
(b) Derive an expression for the potential at a point along the axial line of a short electric dipole?
Ans. (a) The surface which has same potential through out is called an equipotential surface.
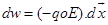
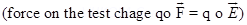
Since work done is moving a test charge along an equipotential surface is always zero.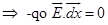
Or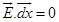
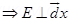
(b) Consider an electric dipole of dipole length 2a and point P on the axial line such that OP= r
where O is the center of the dipole.
Electric Potential at point P due to the dipole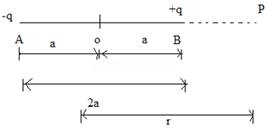
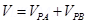
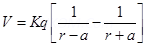
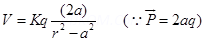
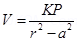
For a short electric dipole (a) can be neglected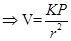
4. Check that the ratio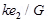 
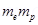is dimensionless. Look up a Table of Physical Constants and determine the value of this ratio. What does the ratio signify?
Ans. The given ratio is 
.
Where,
G = Gravitational constant
Its unit is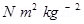 
= Masses of electron and proton.
Their unit is kg.
e = Electric charge.
Its unit is C.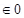
= Permittivity of free space
Its unit is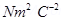 
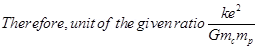
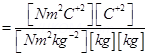
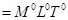
Hence, the given ratio is dimensionless.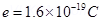
G =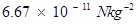 
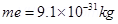
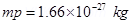
Hence, the numerical value of the given ratio is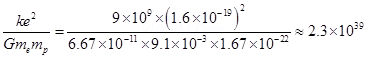
This is the ratio of electric force to the gravitational force between a proton and an electron, keeping distance between them constant.
5. Four point charges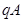 
= 
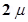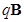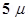C, 
= – 
C,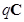 
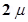= C, and 
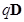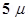= – C are located at the corners of a square ABCD of side 10 cms. What is the force on a charge of 1 
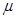C placed at the centre of the square?
Ans. The given figure shows a square of side 10 cm with four charges placed at its corners. O is the centre of the square.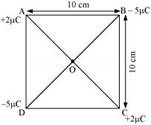
Where,
(Sides)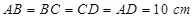 
(Diagonal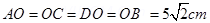s) 
s
A charge of amount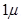 
C is plasced at point O.
Force of repulsion between charges placed at corner A and centre O is equal in magnitude but opposite in direction relative to the force of repulsion between the charges placed at corner C and centre O. Hence, they will cancel each other. Similarly, force of attraction between charges placed at corner B and centre O is equal in magnitude but opposite in direction relative to the force of attraction between the charges placed at corner D and centre O. Hence, they will also cancel each other. Therefore, net force caused by the four charges placed at the corner of the square on 1 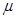C charge at centre O is zero.
6. Two point charges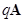 
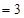
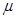C and 
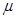
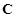are located 20 cm apart in vacuum.
(a) What is the electric field at the midpoint O of the line AB joining the two charges?
(b) If a negative test charge of magnitude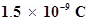 
is placed at this point, what is the force experienced by the test charge?
Ans. (a) The situation is represented in the given figure. O is the mid-point of line AB.
Distance between the two charges,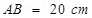 
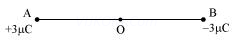
Net electric field at point 
Electric field at point O caused by +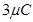
charge,
= 
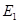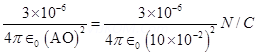along OB
Where,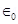
= Permittivity of free space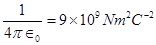
Magnitude of electric field at point O caused by – 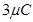charge,
= 
= 
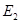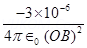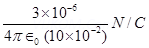along OB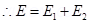
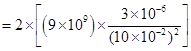[since the values 
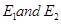of are same, the value is multiplied with2]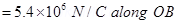
Therefore, the electric field at mid-point O is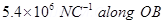 
(b) A test charge of amount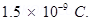 
is placed at mid-point O.
Force experienced by the test charge = F
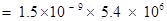
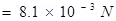
The force is directed along line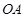 
. This is because the negative test charge is repelled by the charge placed at point B but attracted towards point A.
Therefore, the force experienced by the test charge is 
along OA.
7. A system has two charges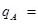 
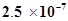C and 
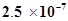C located at points A: 
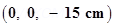and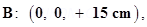 
respectively. What are the total charge and electric dipole moment of the system?
Ans. Both the charges can be located in a coordinate frame of reference as shown in the given figure.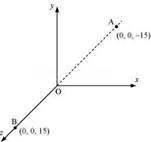
At A, amount of charge,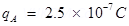 
At B, amount of charge,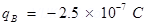 
Total charge of the system,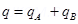
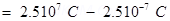
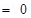
Distance between two charges at points A and B,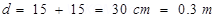
Electric dipole moment of the system is given by,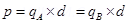
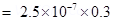
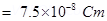along positive z-axis
Therefore, the electric dipole moment of the system is 
m along positive z-axis.
8. (a) Two insulated charged copper spheres A and B have their centers separated by a distance of 50 cm. What is the mutual force of electrostatic repulsion if the charge on each is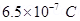 
s? The radii of A and B are negligible compared to the distance of separation.
(b) What is the force of repulsion if each sphere is charged double the above amount, and the distance between them is halved?
Ans. (a) Charge on sphere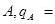 
Charge on sphere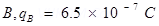 
Distance between the spheres,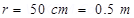 
Force of repulsion between the two spheres,
Where,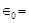
Free space permittivity
=
∴
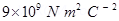
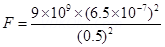
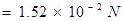
Therefore, the force between the two spheres is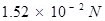 
(b) After doubling the charge, charge on sphere 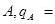Charge on sphere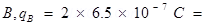 
The distance between the spheres is halved.
∴
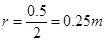
Force of repulsion between the two spheres,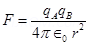
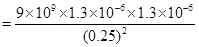
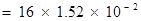
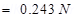s
Therefore, the force between the two spheres is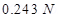 
9. Suppose the spheres A and B in Exercise 1.12 have identical sizes. A third sphere of the same size but uncharged is brought in contact with the first, then brought in contact with the second, and finally removed from both. What is the new force of repulsion between A and B?
Ans. Distance between the spheres,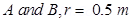 
Initially, the charge on each sphere,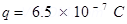 
When sphere A is touched with an uncharged sphere C, amount of charge from A will transfer to sphere
C. Hence, charge on each of the spheres, A and C,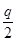 
.
When sphere C with charge 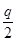is brought in contact with sphere B with charge q, total charges on the system will divide into two equal halves given as,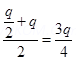
Each sphere will share each half. Hence, charge on each of the spheres, C and B, is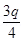
.
Force of repulsion between sphere A having charge 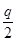and sphere B having charge=
=
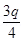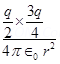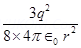
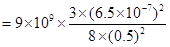
Therefore, the force of attraction between the two spheres is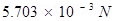
.
10. Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude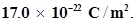 
What is E: (a) in the outer region of the first plate, (b) in the outer region of the second plate, and (c) between the plates?
Ans. The situation is represented in the following figure.
A and B are two parallel plates close to each other. Outer region of plate A is labelled as I, outer region of plate B is labelled as III, and the region between the plates, A and B, is labelled as II.
Charge density of plate A, 
Charge density of plate B, 
In the regions, I and III, electric field E is zero. This is because charge is not enclosed by the respective plates.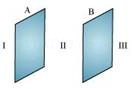
Electric field E in region II is given by the relation,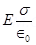
Where,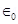=Permittivity of free space =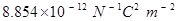
∴
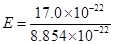
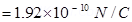
Therefore, electric field between the plates is .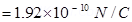
11. An oil drop of 12 excess electrons is held stationary under a constant electric field of 
in Millikan’s oil drop experiment. The density of the oil is 1.26 g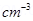 
. Estimate the radius of the drop. 
Ans. Excess electrons on an oil drop, n = 12
Electric field intensity, E =
Density of oil, 
Acceleration due to gravity, g 
Charge on an electron, e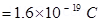 
Radius of the oil drop = r
Force (F) due to electric field E is equal to the weight of the oil drop (W)
F = W
Eq = mg
Ene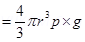 
Where,
q = Net charge on the oil drop = ne
m = Mass of the oil drop
= Volume of the oil drop × Density of oil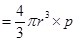
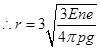
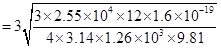
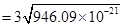
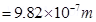
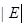
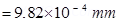
Therefore, the radius of the oil drop is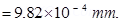 
12. In a certain region of space, electric field is along the z-direction throughout. The magnitude of electric field is, however, not constant but increases uniformly along the positive z-direction, at the rate of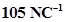 
per metre. What are the force and torque experienced by a system having a total dipole moment equal to 
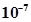Cm in the negative z-direction?
Ans. Dipole moment of the system, p = q × dl =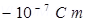 
Rate of increase of electric field per unit length,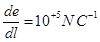
Force (F) experienced by the system is given by the relation,
F = qE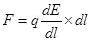
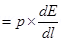
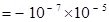
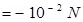
The force is 
in the negative z-direction i.e., opposite to the direction of electric field. Hence, the angle between electric field and dipole moment is 180°.
Torque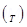 
is given by the relation, 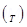= pE sin180°
= 0
Therefore, the torque experienced by the system is zero.
13. (a) A conductor A with a cavity as shown in Fig. 1.36(a) is given a charge Q. Show that the entire charge must appear on the outer surface of the conductor. (b) Another conductor B with charge q is inserted into the cavity keeping B insulated from A. Show that the total charge on the outside surface of A is Q + q [Fig. 1.36(b)]. (c) A sensitive instrument is to be shielded from the strong electrostatic fields in its environment. Suggest a possible way.
Ans. (a) Let us consider a Gaussian surface that is lying wholly within a conductor and enclosing the cavity. The electric field intensity E inside the charged conductor is zero.
Let q is the charge inside the conductor and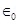 
is the permittivity of free space.
According to Gauss’s law,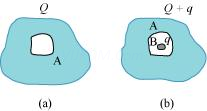
Flux,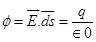 
Here, E = 0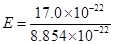
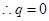
Therefore, charge inside the conductor is zero.
The entire charge Q appears on the outer surface of the conductor.
(b) The outer surface of conductor A has a charge of amount Q. Another conductor B having charge +q is kept inside conductor A and it is insulated from A. Hence, a charge of amount – q will be induced in the inner surface of conductor A and +q is induced on the outer surface of conductor A. Therefore, total charge on the outer surface of conductor A is Q + q.
(c) A sensitive instrument can be shielded from the strong electrostatic field in its environment by enclosing it fully inside a metallic surface. A closed metallic body acts as an electrostatic shield.
14. A hollow charged conductor has a tiny hole cut into its surface. Show that the electric field in the hole is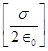 
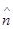, where 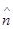is the unit vector in the outward normal direction, and 
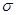is the surface charge density near the hole.
Ans. Let us consider a conductor with a cavity or a hole. Electric field inside the cavity is zero.Let E is the electric field just outside the conductor, q is the electric charge, 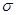is the charge density, and 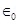is the permittivity of free space.
Charge 
According to Gauss’s law,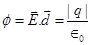
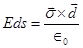
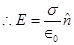
Therefore, the electric field just outside the conductor is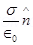
. This field is a superposition of field due to the cavity 
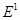and the field due to the rest of the charged conductor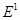. These fields are equal and opposite inside the conductor, and equal in magnitude and direction outside the conductor.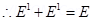
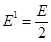
Therefore, the field due to the rest of the conductor is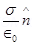
.
Hence, proved.
15. Obtain the formula for the electric field due to a long thin wire of uniform linear charge density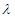 
without using Gauss’s law. [Hint: Use Coulomb’s law directly and evaluate the necessary integral.]
Ans. Take a long thin wire XY (as shown in the figure) of uniform linear charge density.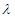
Consider a point A at a perpendicular distance l from the mid-point O of the wire, as shown in the following figure.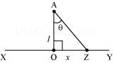
Let E be the electric field at point A due to the wire, XY.
Consider a small length element dx on the wire section with OZ = x
Let q be the charge on this piece.
Electric field due to the piece,
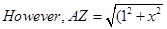
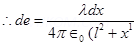
The electric field is resolved into two rectangular components.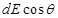 
is the perpendicular component and 
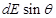is the parallel component.
When the whole wire is considered, the component 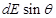is cancelled.
Only the perpendicular component 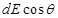affects point A.
Hence, effective electric field at point A due to the element dx is dE1.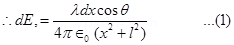
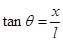
On differentiating equation (2), we obtain
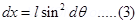
From equation (2),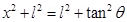
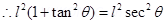
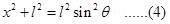
Putting equations (3) and (4) in equation (1), we obtain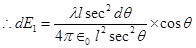
The wire is so long that tends from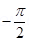 
to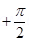 
.
By integrating equation (5), we obtain the value of field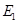 
as,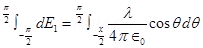
Therefore, the electric field due to long wire is 
16. It is now believed that protons and neutrons (which constitute nuclei of ordinary matter) are themselves built out of more elementary units called quarks. A proton and a neutron consist of three quarks each. Two types of quarks, the so called ‘up’ quark (denoted by u) of charge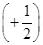 
e, and the ‘down’ quark (denoted by d) of charge (-1/3) e, together with electrons build up ordinary matter. (Quarks of other types have also been found which give rise to different unusual varieties of matter.) Suggest a possible quark composition of a proton and neutron.
Ans.A proton has three quarks. Let there be n up quarks in a proton, each having a charge of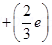
.
Charge due to n up quarks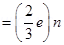
Number of down quarks in a proton = 3 – n
Each down quark has a charge of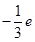 
.
Charge due to (3 – n) down quarks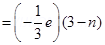 
Total charge on a proton = + e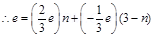
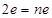
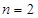
Number of up quarks in a proton, n = 2
Number of down quarks in a proton = 3 – n = 3 – 2 = 1
Therefore, a proton can be represented as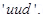
A neutron also has three quarks. Let there be n up quarks in a neutron, each having a charge of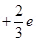 
.
Charge on a neutron due to n up quarks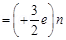 
Number of down quarks is 3 – n, each having a charge of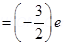 
.
Charge on a neutron due to 
down quarks =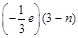 
Total charge on a neutron = 0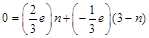
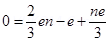
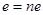
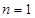
Number of up quarks in a neutron, n = 1
Number of down quarks in a neutron = 3 – n = 2
Therefore, a neutron can be represented as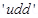
.
17. (a) Consider an arbitrary electrostatic field configuration. A small test charge is placed at a null point (i.e., where E = 0) of the configuration. Show that the equilibrium of the test charge is necessarily unstable.
(b) Verify this result for the simple configuration of two charges of the same magnitude and sign placed a certain distance apart.
Ans. A proton has three quarks. Let there be n up quarks in a proton, each having a charge of
.
Charge due to n up quarks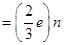
Number of down quarks in a proton = 3 – n
Each down quark has a charge of .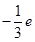
Charge due to (3 – n) down quarks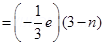 
Total charge on a proton = + e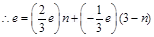
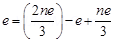
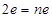
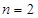
Number of up quarks in a proton, n = 2
Number of down quarks in a proton = 3 – n = 3 – 2 = 1
Therefore, a proton can be represented as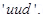
A neutron also has three quarks. Let there be n up quarks in a neutron, each having a charge of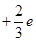 
.
Charge on a neutron due to n up quarks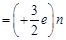 
Number of down quarks is 3 – n, each having a charge of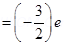 
.
Charge on a neutron due to down quarks =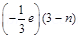 
Total charge on a neutron = 0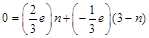
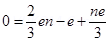
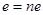
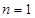
Number of up quarks in a neutron, n = 1
Number of down quarks in a neutron = 3 – n = 2
Therefore, a neutron can be represented as.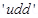
18. A particle of mass m and charge ( – q) enters the region between the two charged plates initially moving along x-axis with speed vx (like particle 1 in Fig. 1.33). The length of plate is L and an uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is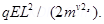 
Compare this motion with motion of a projectile in gravitational field discussed in Section 4.10 of Class XI Textbook of Physics.
Ans. Charge on a particle of mass m = – q
Velocity of the particle = vx
Length of the plates =L
Magnitude of the uniform electric field between the plates = E
Mechanical force, F = Mass (m) × Acceleration (a)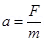
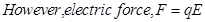
Therefore, acceleration, 
Time taken by the particle to cross the field of length L is given by,
t
In the vertical direction, initial velocity, u = 0
According to the third equation of motion, vertical deflection s of the particle can be obtained as,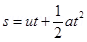
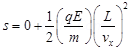
Hence, vertical deflection of the particle at the far edge of the plate is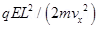
. This is similar to the motion of horizontal projectiles under gravity.