IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 2.2 – Forces
Topic 2 Weightage : 9 %
All Questions for Topic 2.3 – Kinetic energy ,Gravitational potential energy ,Elastic potential energy ,Work done as energy transfer ,Power as rate of energy transfer ,Principle of conservation of energy ,Efficiency
Question
A mass is released from the top of a smooth ramp of height h. After leaving the ramp, the mass slides on a rough horizontal surface.
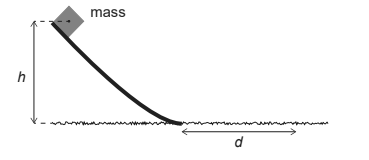
The mass comes to rest in a distance d. What is the coefficient of dynamic friction between the mass and the horizontal surface?
A
B
C
D
▶️Answer/Explanation
Ans: D
Climbing down the inclined plane
External Non conservative forces = 0
\(KE_i = 0 ; \; PE_i= mgh\)
\(KE_f=K;\; PE_f=0\)
By conservation of Mechanical energy, we have \(K=mgh\)
Motion on Rough Surface
External Non conservative force = Friction = \(-\mu mg\)
Distance travelled =d
Work done = \(F\;\Delta x=-\mu mgd \)
Hence Kinetic energy is used against the work done by frictional force
hence \(\mu mgd =mgh\)
or \(\mu ==\frac{h}{d}\)
Question
A car takes 20 minutes to climb a hill at constant speed. The mass of the car is 1200 kg and the car gains gravitational potential energy at a rate of 6.0 kW. Take the acceleration of gravity to be 10 m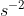 
. What is the height of the hill?
A 0.6 m
B 10 m
C 600 m
D. 6000 m
▶️Answer/Explanation
Ans: C
Question
Which statement applies to an object in translational equilibrium?
A. The object must be stationary.
B. The object must be moving with constant acceleration.
C. The resultant force acting on the object must be zero.
D. There must be no external forces acting on the object.
▶️Answer/Explanation
Markscheme
C
Ref: https://www.iitianacademy.com/ib-physics-unit-2-mechanics-forces-dynamics-notes/
and 
An object is said to be in equilibrium when there is no external net force acting on it. When an object is in equilibrium, it does not accelerate. If it had a velocity, the velocity remains constant; if it was at rest, it remains at rest.
If all the forces acting on a particular object add up to zero and have no resultant force, then it’s in translational equilibrium. Examples would be a book resting on a bookshelf, or someone walking at a steady, constant speed.
An object that’s not rotating or doing so at a steady speed, the sum of the torques acting on it equaling zero, is at rotational equilibrium. Some examples of this are a Ferris wheel turning at a constant velocity, two children of equal weight balanced on either side of a seesaw, or the Earth rotating on its axis at a steady speed
Question
The resultant force acting on an object of mass 5.0kg varies with time as shown. The object is initially at rest.
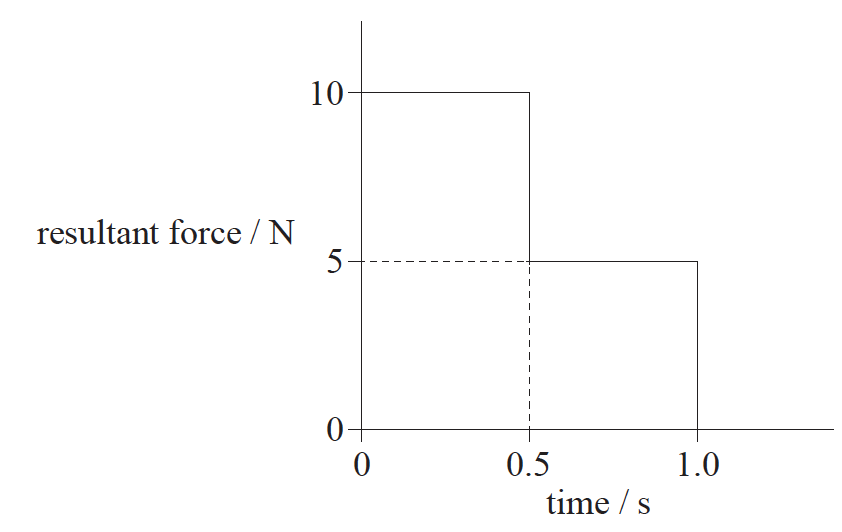
What is the speed of the object after 1.0 s?
A. 0.50ms–1
B. 1.0ms–1
C. 1.5ms–1
D. 2.0ms–1
▶️Answer/Explanation
Markscheme
C
Ref: https://www.iitianacademy.com/ib-physics-topic-2-mechanics-2-4-momentum-and-impulse-study-notes/
impulse is the area under the F – t curve for ones dimensional motion.
and implulse = Change in Momentum
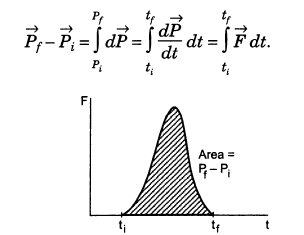
Area under curve = \(10 \times 0.5 + 5 \times 0.5 = 7.5\)
Change in momentum = \(m(v_f-v_i) = mv\)
\(v=\frac{7.5}{m}=\frac{7.5}{5}=1.5\; m/s\)
Question
A speed boat tows a water skier so that the skier accelerates.
The magnitude of the force exerted on the skier by the tow rope must be
I. greater than the magnitude of the total resistive force acting on the skier
II. equal to the magnitude of the force exerted on the tow rope by the skier
III. equal to the magnitude of the force causing the boat to accelerate.
Which of the above factors is/are correct?
A. I and II only
B. I and III only
C. II only
D. III only
▶️Answer/Explanation
Markscheme
A
Free body diagram is given as below
Hence in order to skier accelerate , Fr should be greater than Ff. Also FB is greater than Fr
Related Links