IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 9.3 Interference
Topic 9 Weightage : 5 %
All Questions for Topic 9.3 – Young’s double-slit experiment , Modulation of two-slit interference pattern by one-slit diffraction effect , Multiple slit and diffraction grating interference patterns , Thin film interference
Question
Light is incident on a diffraction grating. The wavelength lines 600.0 nm and 601.5 nm are just resolved in the second order spectrum. How many slits of the diffraction grating are illuminated?
A 20
B 40
C. 200
D. 400
▶️Answer/Explanation
Ans: C
Refer: https://www.iitianacademy.com/ib-unit-9-wave-phenomena-diffraction-interference-notes/
\(R= Nm =\frac{\lambda_{avg}}{\Delta \lambda}\)
In Given question
\(\lambda_1 = 600.0 nm , \lambda_2 = 601.5 \; nm\)
Hence \(\Delta \lambda = \lambda_2-\lambda_1\)
\(=601.5-600.0 = 1.5 \times 10^{-9}\)
also \(m= 2\)
\(\lambda_{avg} =\frac{\lambda_1+\lambda_2}{2}=\frac{601.5+600.0}{2} \approx 600 \times 10^{-9}\)
Putting in equation these values
\(Nm =\frac{\lambda_{avg}}{\Delta \lambda}\)
\(\therefore N= \frac{600 \times 10^{-9}}{2 \times 1.5 \times 10^{-9}}=\frac{600}{3}=200\)
Question
In a double-slit interference experiment, the following intensity pattern is observed for light of wavelength λ.
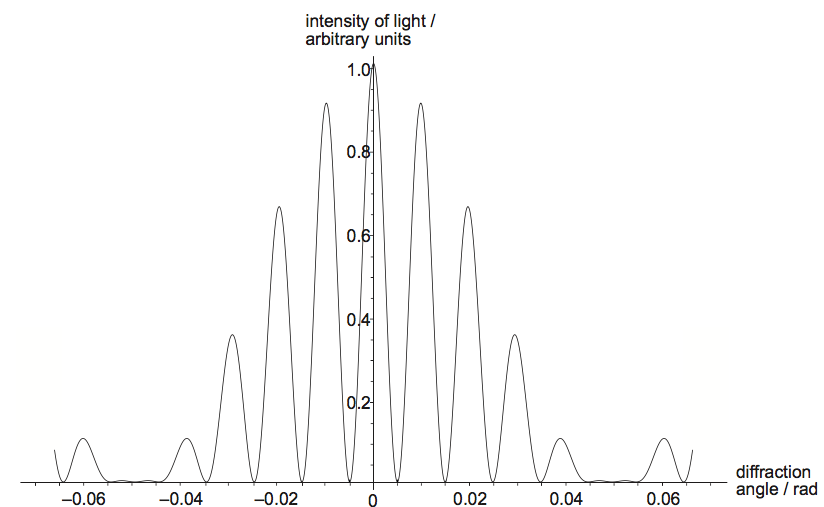
The distance between the slits is d. What can be deduced about the value of the ratio \(\frac{\lambda }{d}\) and the effect of single-slit diffraction in this experiment?
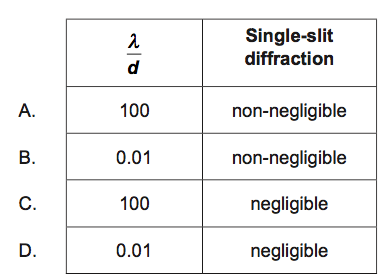
▶️Answer/Explanation
Markscheme
B
\(d sin\theta = m \lambda \; maxima \; for \; m= \pm 1 ,\pm 2 etc.\)
for small \(\theta\)
\(d \; \theta = m \lambda\)
or
\(\frac{\lambda}{d } =\frac{\theta}{m}\)
for \(m =1\)
\(\frac{\lambda}{d } =\theta\)
Hence in given question
\(\theta = 0.01\)
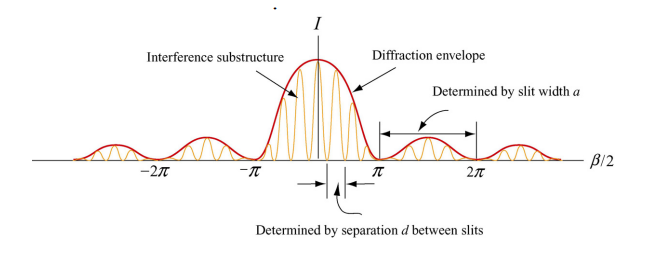
We have seen that the interference maxima occur when d sinθ = mλ . On the other hand, the condition for the first diffraction minimum is a sinθ = λ . Thus, a particular interference maximum with order number m may coincide with the first diffraction minimum. The value of m may be obtained as:
\(\frac{d \; sin \theta}{a\; sin\theta}=\frac{m \lambda}{ \lambda}\)
or
\(m = \frac{d}{a}\)
Hence \(mth \) fringe will not be seen. Hence effect of single-slit diffraction in this experiment is non negligible
Question
A parallel beam of monochromatic light of wavelength λ passes through a slit of width b and forms a diffraction pattern on a screen far from the slit. The angle at which the first diffraction minimum is f\med is θ.
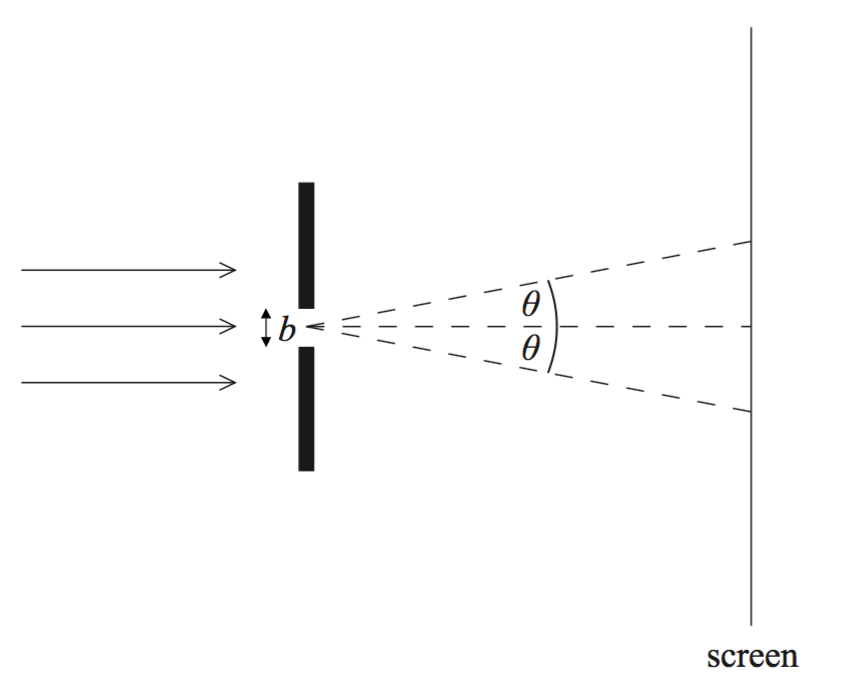
Which of the following changes in λ and b, carried out separately, will increase the value of θ?
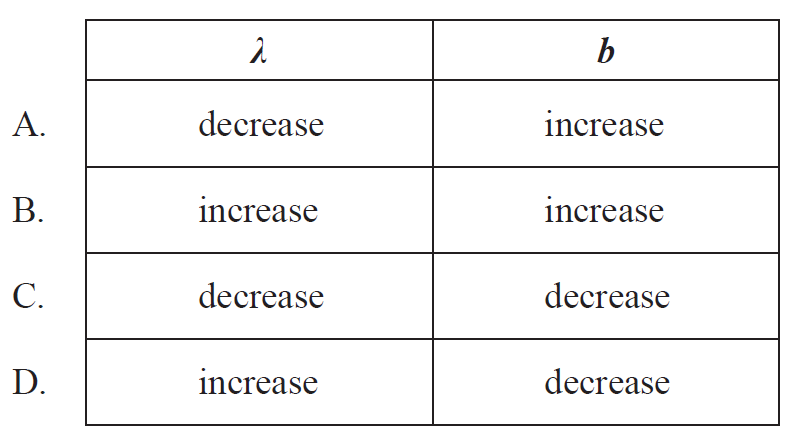
▶️Answer/Explanation
Markscheme
D
we have equation for diffraction minima as
\(b sin \theta = n \lambda\)
Hence \(b sin \theta = \lambda\) (first minimum)
or
\(sin \theta \approx \theta =\frac{\lambda}{b}\)
\(\therefore \theta \uparrow \; if \lambda\uparrow or \; b \downarrow\)
Question
A coherent beam of light of wavelength λ is incident on a double slit. The width of the slits is small compared to their separation. An interference pattern is observed on a distant screen. O is the mid point of the screen.
There is a bright fringe at O and a bright fringe at P. Between O and P there are three dark fringes.
Which of the following is the path difference between the light from the two slits arriving at P?
A. 1.5 λ
B. 2 λ
C. 3 λ
D. 4 λ
▶️Answer/Explanation
Markscheme
C
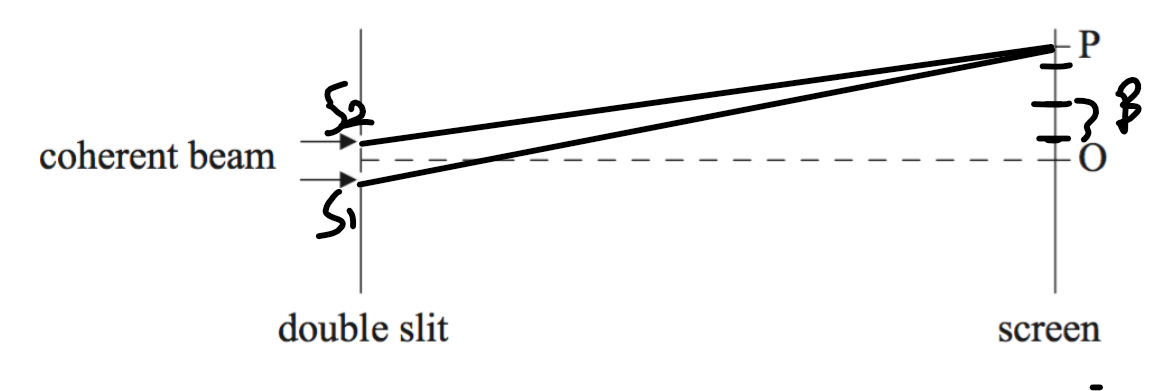
Fringe width is \(\beta \)
\(\beta\) is given by
\(\beta = \frac{\lambda D}{d}\)
In given problem , \(\bar{OP}=y=\frac{\beta }{2}+\beta+\beta+\frac{\beta }{2}\)
\(=3\beta =3 \frac{\lambda D}{d}\)
Path difference is given by
\(S_2P – S_1P= \frac{yd}{D} =3 \frac{\lambda D}{d} \times\frac{d}{D} =3 \lambda\)
Question
A beam of monochromatic light is incident on a diffraction grating of N lines per unit length. The angle between the first orders is θ1.
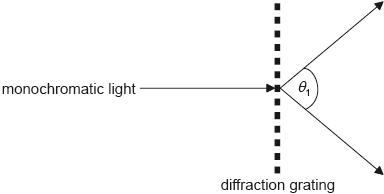
What is the wavelength of the light?
A. \(\frac{{\sin {\theta _1}}}{N}\)
B. N sin θ1
C. N sin\(\left( {\frac{{{\theta _1}}}{2}} \right)\)
D. \(\frac{{\sin \left( {\frac{{{\theta _1}}}{2}} \right)}}{N}\)
▶️Answer/Explanation
Markscheme
D
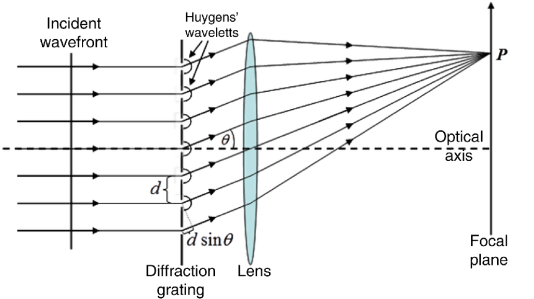
\(d sin\theta = m \lambda\) for \(m= 0,1,2,3\) (maxima – line)
for \(1 st\) order m =1
\(d sin\theta = \lambda\)
Now \(\theta = \frac{\theta_1}{2} \) (\(\theta_1\) is for Both side of central maxima) also \(d=\frac{1}{N}\)
Hence
\(\lambda = \frac{sin \frac{\theta_1}{2}}{N}\)