IB DP PHYSICS 2025 SL&HL – Study notes- All Topics
Topic 4.1 Kinematics of rotational motion
Topic 1 Weightage : XX
Notes for 4.1 Kinematics of rotational motion – Only for Higher Level (HL)
torque τ of a force about an axis as given by τ = Fr sin θ, rotational equilibrium, unbalanced torque, angular acceleration, angular displacement, angular velocity, equations of motion for uniform angular acceleration, moment of inertia, Newton’s second law for rotation, angular momentum, resultant torque, kinetic energy of rotational motion
- IB DP Physics 2025 SL- IB Style Practice Questions with Answer-Topic Wise-Paper 1
- IB DP Physics 2025 HL- IB Style Practice Questions with Answer-Topic Wise-Paper 1
- IB DP Physics 2025 SL- IB Style Practice Questions with Answer-Topic Wise-Paper 2
- IB DP Physics 2025 HL- IB Style Practice Questions with Answer-Topic Wise-Paper 2
1.2 Uniformly accelerated motion: the equations of kinematics
2.3 Acceleration
The notion of acceleration emerges when a change in elocity is combined with the time during which the change occurs.


DEFINITION OF AVERAGE ACCELERATION
$
\overrightarrow{\overrightarrow{\mathbf{a}}}=\frac{\overrightarrow{\mathbf{v}}-\overrightarrow{\mathbf{v}}_o}{t-t_o}=\frac{\Delta \overrightarrow{\mathbf{v}}}{\Delta t}
$

Example 3
Acceleration and Increasing Velocity
Determine the average acceleration of the plane.
▶️Answer/Explanation
$
\begin{gathered}
\overrightarrow{\mathbf{v}}_o=0 \mathrm{~m} / \mathrm{s} \quad \overrightarrow{\mathbf{v}}=260 \mathrm{~km} / \mathrm{h} \quad t_o=0 \mathrm{~s} \quad t=29 \mathrm{~s} \\
\overline{\overrightarrow{\mathbf{a}}}=\frac{\overrightarrow{\mathbf{v}}-\overrightarrow{\mathbf{v}}_o}{t-t_o}=\frac{260 \mathrm{~km} / \mathrm{h}-0 \mathrm{~km} / \mathrm{h}}{29 \mathrm{~s}-0 \mathrm{~s}}=+9.0 \frac{\mathrm{km} / \mathrm{h}}{\mathrm{s}}
\end{gathered}
$

Example 3

Acceleration and Decreasing Velocity
$
\overline{\overrightarrow{\mathbf{a}}}=\frac{\overrightarrow{\mathbf{v}}-\overrightarrow{\mathbf{v}}_o}{t-t_o}=\frac{13 \mathrm{~m} / \mathrm{s}-28 \mathrm{~m} / \mathrm{s}}{12 \mathrm{~s}-9 \mathrm{~s}}=-5.0 \mathrm{~m} / \mathrm{s}^2
$

2.4 Equations of Kinematics for Constant Acceleration
$
\overline{\overrightarrow{\mathbf{v}}}=\frac{\overrightarrow{\mathbf{x}}-\overrightarrow{\mathbf{x}}_o}{t-t_o} \quad \overline{\overrightarrow{\mathbf{a}}}=\frac{\overrightarrow{\mathbf{v}}-\overrightarrow{\mathbf{v}}_o}{t-t_o}
$
For one dimensional motion it is customary to dispense with the use of boldface symbols overdrawn with arrows for the displacement, velocity, and acceleration vectors. We will, however, continue to convey the directions with a plus or minus sign.
\(v=\frac{x-x_o}{t-t_o} \quad a=\frac{v-v_o}{t-t_o}\)
Let the object be at the origin when the clock starts.
$
x_o=0 \quad t_o=0
$
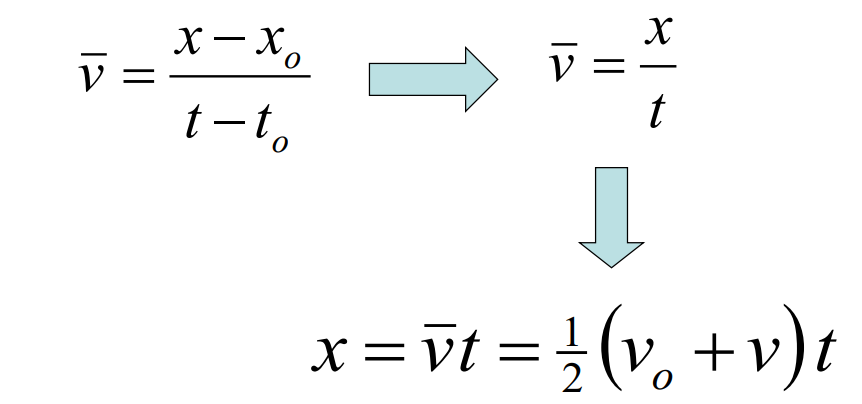
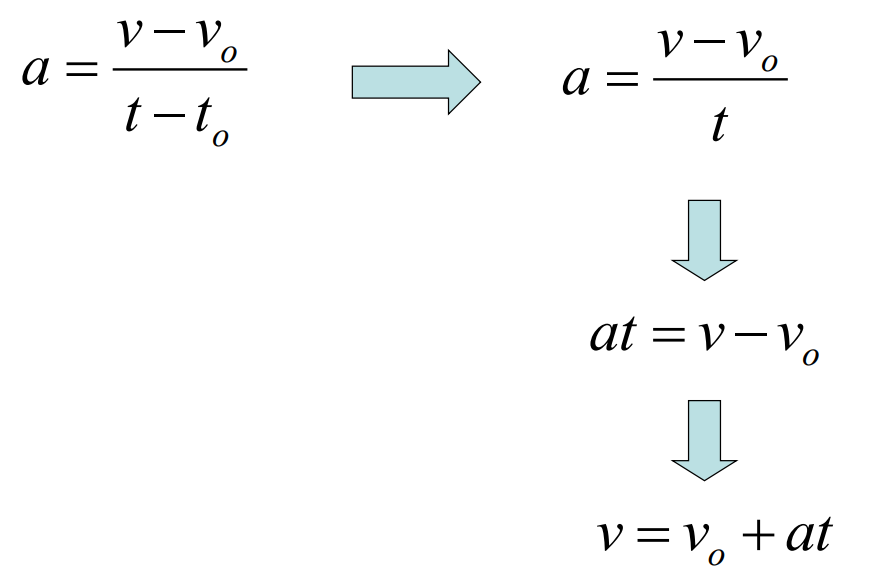
Five kinematic variables:
1. displacement, \(x\)
2. acceleration (constant), a
3. final velocity (at time \(t\) ), \(v\)
4. initial velocity, \(v_0\)
5. elapsed time, \(t\)
\(v=v_o+a t\)
\(x=\frac{1}{2}\left(v_o+v\right) t=\frac{1}{2}\left(v_o+v_o+a t\right) t\)
\(x=v_o t+\frac{1}{2} a t^2\)

\(\begin{aligned} & x=v_o t+\frac{1}{2} a t^2 \\ & =(6.0 \mathrm{~m} / \mathrm{s})(8.0 \mathrm{~s})+\frac{1}{2}\left(2.0 \mathrm{~m} / \mathrm{s}^2\right)(8.0 \mathrm{~s})^2 \\ & =+110 \mathrm{~m}\end{aligned}\)

Example 6
Catapulting a Jet
Find its displacement.
▶️Answer/Explanation
$
\begin{array}{cc}
v_o=0 \mathrm{~m} / \mathrm{s} & a=+31 \mathrm{~m} / \mathrm{s}^2 \\
x=? ? & v=+62 \mathrm{~m} / \mathrm{s}
\end{array}
$
\(a=\frac{v-v_o}{t}\)
\(t=\frac{v-v_o}{a}\)
\(x=\frac{1}{2}\left(v_o+v\right) t=\frac{1}{2}\left(v_o+v\right) \frac{\left(v-v_o\right)}{a}\)
\(x=\frac{v^2-v_o^2}{2 a}\)

\(x=\frac{v^2-v_o^2}{2 a}=\frac{(62 \mathrm{~m} / \mathrm{s})^2-(0 \mathrm{~m} / \mathrm{s})^2}{2\left(31 \mathrm{~m} / \mathrm{s}^2\right)}=+62 \mathrm{~m}\)
Equations of Kinematics for Constant Acceleration
$
\begin{aligned}
& v=v_o+a t \\
& x=\frac{1}{2}\left(v_o+v\right) t \\
& v^2=v_o^2+2 a x \\
& x=v_o t+\frac{1}{2} a t^2
\end{aligned}
$
2.5 Applications of the Equations of Kinematics
Reasoning Strategy
1. Make a drawing.
2. Decide which directions are to be called positive \((+)\) and negative (-).
3. Write down the values that are given for any of the five kinematic variables.
4. Verify that the information contains values for at least three of the five kinematic variables. Identify the desired unknown variable and select the appropriate equation.
5. When the motion is divided into segments, remember that the final velocity of one segment is the initial velocity for the next.
6. Keep in mind that there may be two possible answers to a kinematics problem.
Example 8
An Accelerating Spacecraft
A spacecraft is traveling with a velocity of \(+3250 \mathrm{~m} / \mathrm{s}\). Suddenly the retrorockets are fired, and the spacecraft begins to slow down with an acceleration whose magnitude is \(10.0 \mathrm{~m} / \mathrm{s}^2\). What is the velocity of the spacecraft when the displacement of the craft is \(+215 \mathrm{~km}\), relative to the point where the retrorockets began firing?
▶️Answer/Explanation



\(v^2=v_o^2+2 a x\)
\(v=\sqrt{v_o^2+2 a x}\)
\(\begin{aligned} & v= \pm \sqrt{(3250 \mathrm{~m} / \mathrm{s})^2+2\left(-10.0 \mathrm{~m} / \mathrm{s}^2\right)(215000 \mathrm{~m})} \\ & = \pm 2500 \mathrm{~m} / \mathrm{s}\end{aligned}\)
2.6 Freely Falling Bodies
In the absence of air resistance, it is found that all bodies at the same location above the Earth fall vertically with the same acceleration. If the distance of the fall is small compared to the radius of the Earth, then the acceleration remains essentially constant throughout the descent.
This idealized motion is called free-fall and the acceleration of a freely falling body is called the acceleration due to gravity.
\(g=9.80 \mathrm{~m} / \mathrm{s}^2 \quad\) or \(\quad 32.2 \mathrm{ft} / \mathrm{s}^2\)

Example 10
A Falling Stone
A stone is dropped from the top of a tall building. After 3.00s of free fall, what is the displacement \(y\) of the stone




\(\begin{aligned} & y=v_o t+\frac{1}{2} a t^2 \\ & =(0 \mathrm{~m} / \mathrm{s})(3.00 \mathrm{~s})+\frac{1}{2}\left(-9.80 \mathrm{~m} / \mathrm{s}^2\right)(3.00 \mathrm{~s})^2 \\ & =-44.1 \mathrm{~m}\end{aligned}\)
Example 12
How High Does it Go?
The referee tosses the coin up with an initial speed of \(5.00 \mathrm{~m} / \mathrm{s}\). In the absence if air resistance, how high does the coin go above its point of release?
▶️Answer/Explanation

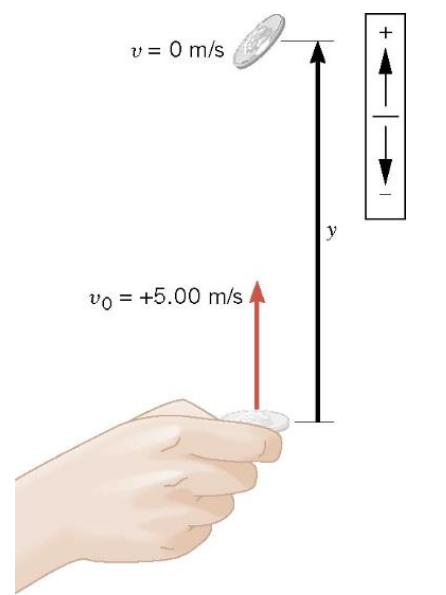


\(v^2=v_o^2+2 a y\)
\(y=\frac{v^2-v_o^2}{2 a}\)
\(y=\frac{v^2-v_o^2}{2 a}=\frac{(0 \mathrm{~m} / \mathrm{s})^2-(5.00 \mathrm{~m} / \mathrm{s})^2}{2\left(-9.80 \mathrm{~m} / \mathrm{s}^2\right)}=1.28 \mathrm{~m}\)
Conceptual Example 14
Acceleration Versus Velocity
There are three parts to the motion of the coin. On the way up, the coin has a vector velocity that is directed upward and has decreasing magnitude. At the top of its path, the coin momentarily has zero velocity. On the way down, the coin has downward-pointing velocity with an increasing magnitude.
In the absence of air resistance, does the acceleration of the coin, like the velocity, change from one part to another?
Conceptual Example 15
Taking Advantage of Symmetry
Does the pellet in part \(b\) strike the ground beneath the cliff with a smaller, greater, or the same speed as the pellet in part \(a\) ?
▶️Answer/Explanation
