IB DP PHYSICS 2025 SL&HL – Study notes- All Topics
Topic 4.1 Kinematics of rotational motion
Topic 1 Weightage : XX
Notes for 4.1 Kinematics of rotational motion – Only for Higher Level (HL)
torque τ of a force about an axis as given by τ = Fr sin θ, rotational equilibrium, unbalanced torque, angular acceleration, angular displacement, angular velocity, equations of motion for uniform angular acceleration, moment of inertia, Newton’s second law for rotation, angular momentum, resultant torque, kinetic energy of rotational motion
- IB DP Physics 2025 SL- IB Style Practice Questions with Answer-Topic Wise-Paper 1
- IB DP Physics 2025 HL- IB Style Practice Questions with Answer-Topic Wise-Paper 1
- IB DP Physics 2025 SL- IB Style Practice Questions with Answer-Topic Wise-Paper 2
- IB DP Physics 2025 HL- IB Style Practice Questions with Answer-Topic Wise-Paper 2
3.1 Displacement, Velocity, and Acceleration

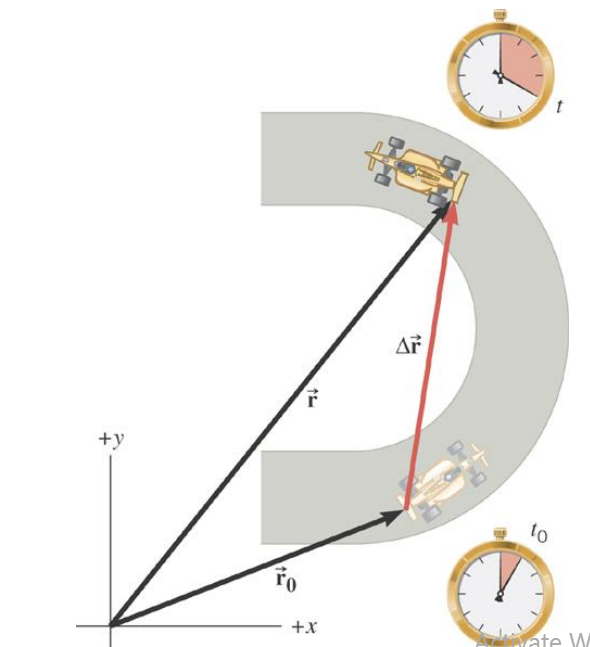
\(\overrightarrow{\mathbf{r}}_o=\) initial position
\(\overrightarrow{\mathbf{r}}=\) final position
\(\Delta \overrightarrow{\mathbf{r}}=\overrightarrow{\mathbf{r}}-\overrightarrow{\mathbf{r}}_o=\) displacement
Average velocity is the displacement divided by the elapsed time.
$
\overline{\overrightarrow{\mathbf{v}}}=\frac{\overrightarrow{\mathbf{r}}-\overrightarrow{\mathbf{r}}_o}{t-t_o}=\frac{\Delta \overrightarrow{\mathbf{r}}}{\Delta t}
$
The instantaneous velocity indicates how fast the car moves and the direction of motion at each instant of time.

\(\overline{\overrightarrow{\mathbf{v}}}=\lim _{\Delta t \rightarrow 0} \frac{\Delta \overrightarrow{\mathbf{r}}}{\Delta t}\)
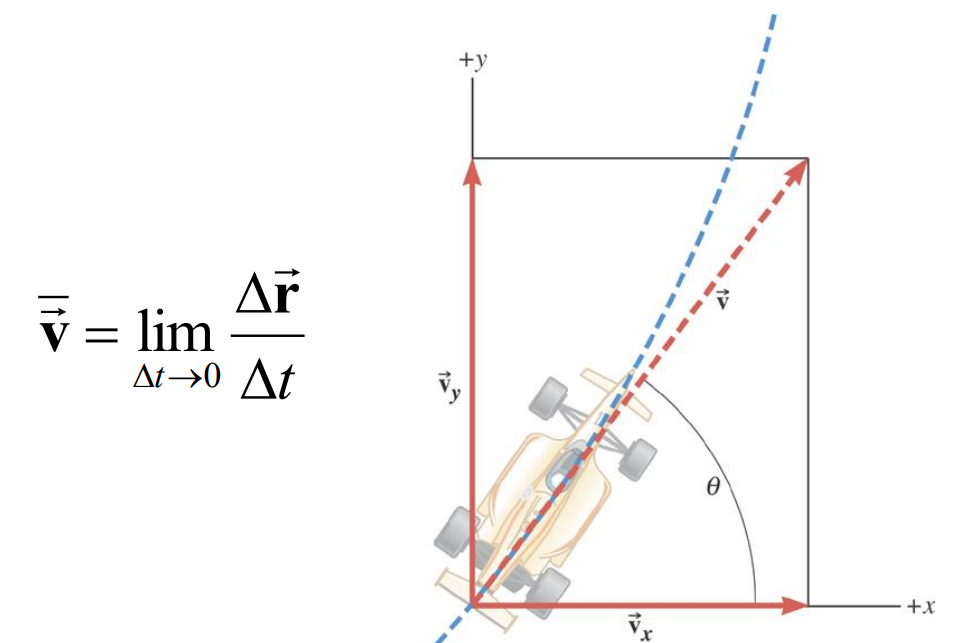
\(\overline{\overrightarrow{\mathbf{v}}}=\lim _{\Delta t \rightarrow 0} \frac{\Delta \overrightarrow{\mathbf{r}}}{\Delta t}\)
DEFINITION OF AVERAGE ACCELERATION
$
\overline{\overrightarrow{\mathbf{a}}}=\frac{\overrightarrow{\mathbf{v}}-\overrightarrow{\mathbf{v}}_o}{t-t_o}=\frac{\Delta \overrightarrow{\mathbf{v}}}{\Delta t}
$

Equations of Kinematics
$
\begin{aligned}
& v=v_o+a t \\
& x=\frac{1}{2}\left(v_o+v\right) t \\
& v^2=v_o^2+2 a x \\
& x=v_o t+\frac{1}{2} a t^2
\end{aligned}
$
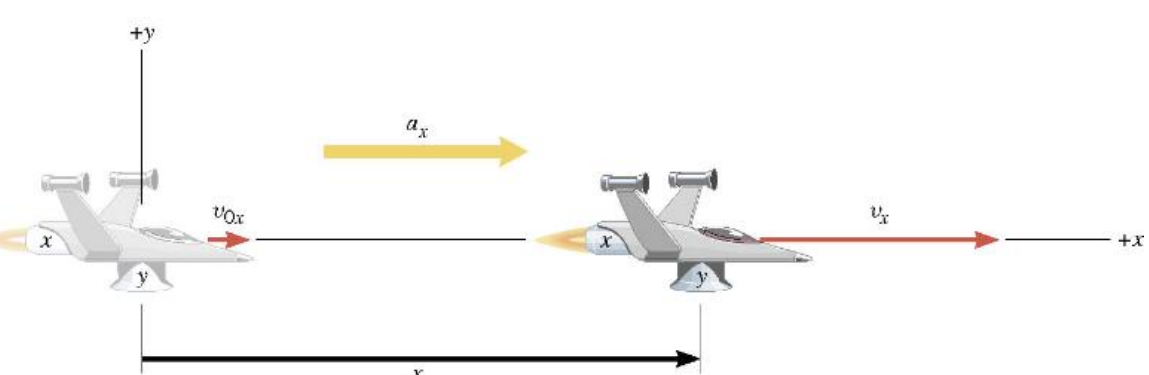
\(v_x=v_{o x}+a_x t \quad x=\frac{1}{2}\left(v_{o x}+v_x\right) t\)
\(x=v_{o x} t+\frac{1}{2} a_x t^2 \quad v_x^2=v_{o x}^2+2 a_x x\)
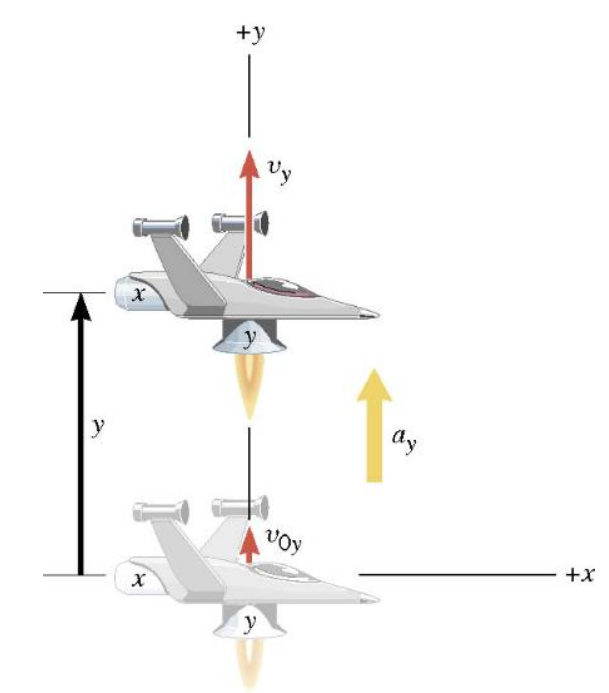
\(\begin{aligned} & v_y=v_{o y}+a_y t \\ & y=v_{o y} t+\frac{1}{2} a_y t^2 \\ & y=\frac{1}{2}\left(v_{o y}+v_y\right) t \\ & v_y^2=v_{o y}^2+2 a_y y\end{aligned}\)

The \(x\) part of the motion occurs exactly as it would if the y part did not occur at all, and vice versa.
Example 1 A Moving Spacecraft
In the \(x\) direction, the spacecraft has an initial velocity component of \(+22 \mathrm{~m} / \mathrm{s}\) and an acceleration of \(+24 \mathrm{~m} / \mathrm{s}^2\). In the \(y\) direction, the analogous quantities are \(+14 \mathrm{~m} / \mathrm{s}\) and an acceleration of \(+12 \mathrm{~m} / \mathrm{s}^2\). At a time \(7.0 \mathrm{~s}\), find (a) \(x\) and \(\mathrm{v}_{\mathrm{x}}\), (b) \(y\) and \(v_y\), and (c) the final velocity of the spacecraft.

Reasoning Strategy
1. Make a drawing.
2. Decide which directions are to be called positive (+) and negative (-).
3. Write down the values that are given for any of the five kinematic variables associated with each direction.
4. Verify that the information contains values for at least three of the kinematic variables. Do this for \(x\) and \(y\). Select the appropriate equation.
5. When the motion is divided into segments, remember that the final velocity of one segment is the initial velocity for the next.
6. Keep in mind that there may be two possible answers to a kinematics problem.
Example 1 A Moving Spacecraft
In the \(x\) direction, the spacecraft has an initial velocity component of \(+22 \mathrm{~m} / \mathrm{s}\) and an acceleration of \(+24 \mathrm{~m} / \mathrm{s}^2\). In the \(y\) direction, the analogous quantities are \(+14 \mathrm{~m} / \mathrm{s}\) and an acceleration of \(+12 \mathrm{~m} / \mathrm{s}^2\). Find (a) \(x\) and \(v_x\), (b) \(y\) and \(v_y\), and (c) the final velocity of the spacecraft at time \(7.0 \mathrm{~s}\).

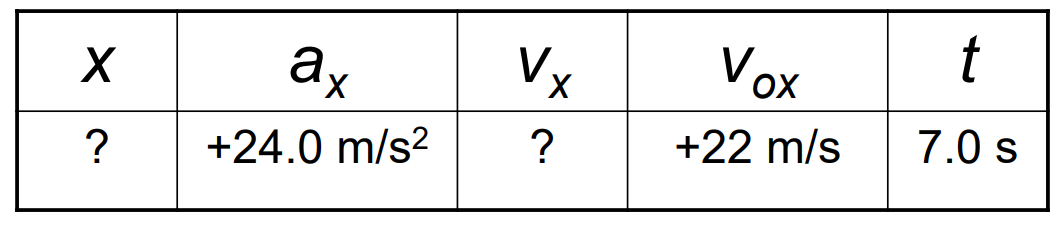
\(\begin{aligned} & x=v_{o x} t+\frac{1}{2} a_x t^2 \\ & =(22 \mathrm{~m} / \mathrm{s})(7.0 \mathrm{~s})+\frac{1}{2}\left(24 \mathrm{~m} / \mathrm{s}^2\right)(7.0 \mathrm{~s})^2=+740 \mathrm{~m} \\ & v_x=v_{o x}+a_x t \\ & =(22 \mathrm{~m} / \mathrm{s})+\left(24 \mathrm{~m} / \mathrm{s}^2\right)(7.0 \mathrm{~s})=+190 \mathrm{~m} / \mathrm{s}\end{aligned}\) 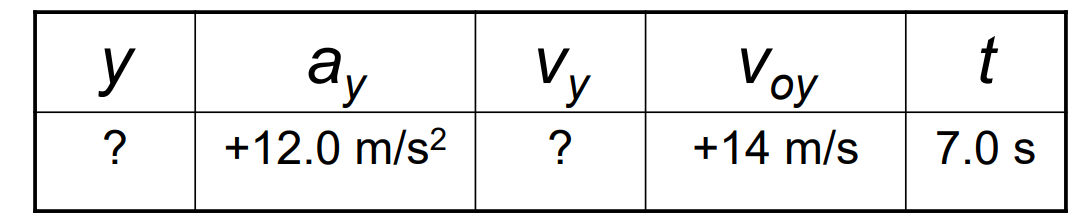
\(\begin{aligned} & y=v_{o y} t+\frac{1}{2} a_y t^2 \\ & =(14 \mathrm{~m} / \mathrm{s})(7.0 \mathrm{~s})+\frac{1}{2}\left(12 \mathrm{~m} / \mathrm{s}^2\right)(7.0 \mathrm{~s})^2=+390 \mathrm{~m} \\ & v_y=v_{o y}+a_y t \\ & =(14 \mathrm{~m} / \mathrm{s})+\left(12 \mathrm{~m} / \mathrm{s}^2\right)(7.0 \mathrm{~s})=+98 \mathrm{~m} / \mathrm{s}\end{aligned}\)
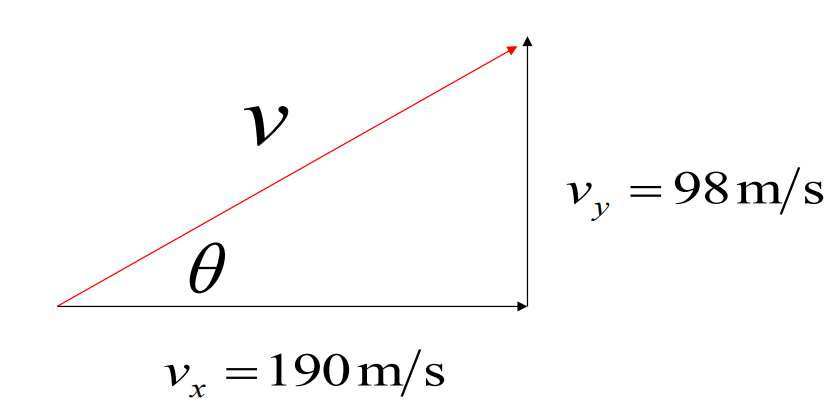
\(\begin{aligned} & v=\sqrt{(190 \mathrm{~m} / \mathrm{s})^2+(98 \mathrm{~m} / \mathrm{s})^2}=210 \mathrm{~m} / \mathrm{s} \\ & \theta=\tan ^{-1}(98 / 190)=27^{\circ}\end{aligned}\)

3.3 Projectile Motion
Under the influence of gravity alone, an object near the surface of the Earth will accelerate downwards at \(9.80 \mathrm{~m} / \mathrm{s}^2\).
$
a_y=-9.80 \mathrm{~m} / \mathrm{s}^2 \quad a_x=0
$
\(v_x=v_{o x}=\) constant
Example 3 A Falling Care Package
The airplane is moving horizontally with a constant velocity of \(+115 \mathrm{~m} / \mathrm{s}\) at an altitude of \(1050 \mathrm{~m}\). Determine the time required for the care package to hit the ground.
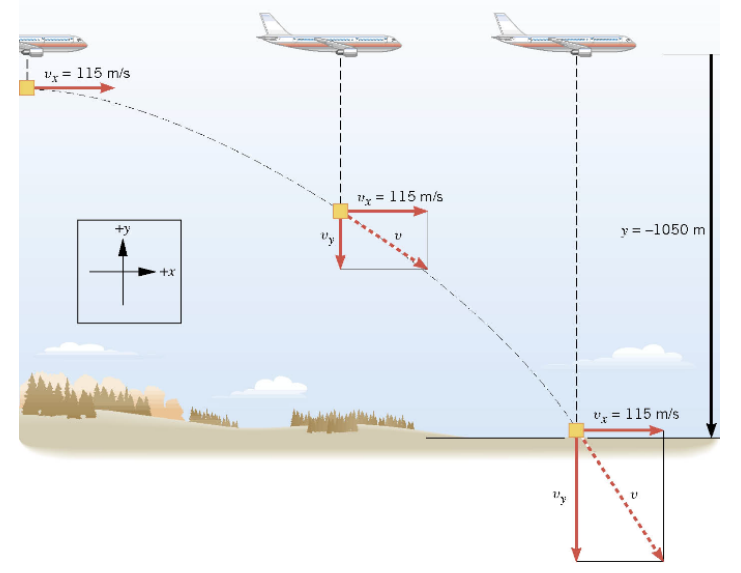

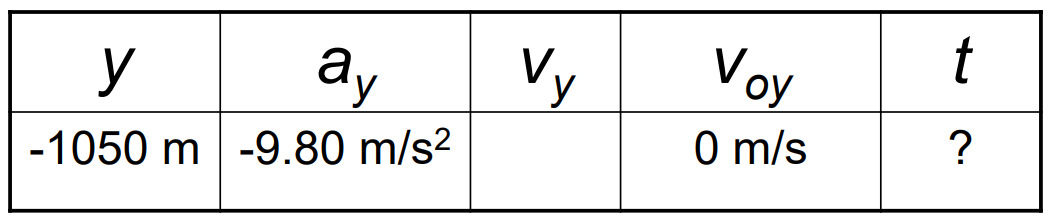

\(\begin{aligned} & y=v_{o y} t+\frac{1}{2} a_y t^2 \longleftrightarrow y=\frac{1}{2} a_y t^2 \\ & t=\sqrt{\frac{2 y}{a_y}}=\sqrt{\frac{2(-1050 \mathrm{~m})}{-9.80 \mathrm{~m} / \mathrm{s}^2}}=14.6 \mathrm{~s}\end{aligned}\)
Example 4 The Velocity of the Care Package
What are the magnitude and direction of the final velocity of the care package?
▶️Answer/Explanation
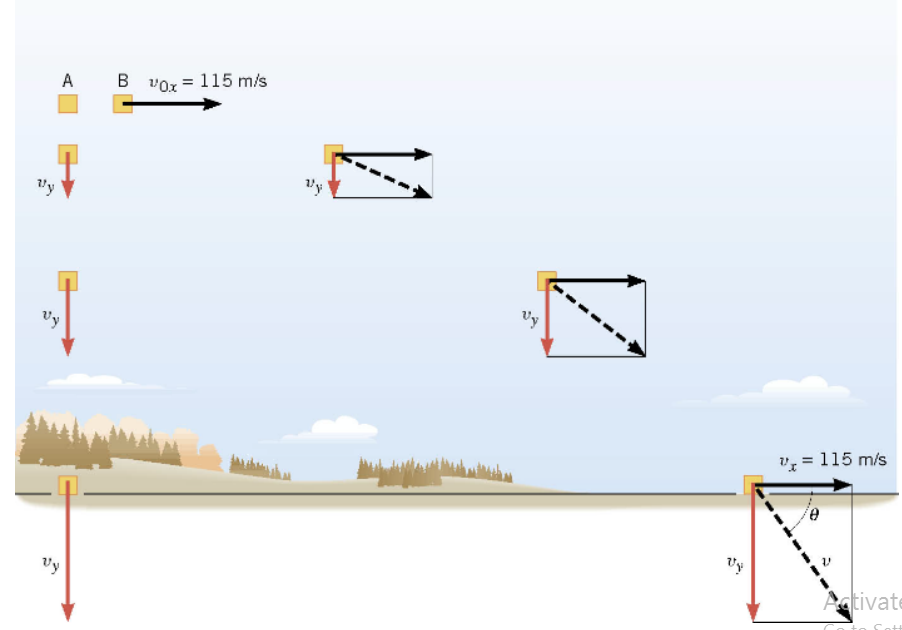

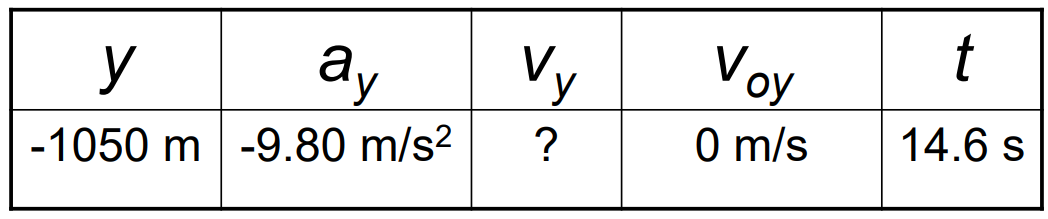

\(\begin{aligned} v_y & =v_{o y}+a_y t=0+\left(-9.80 \mathrm{~m} / \mathrm{s}^2\right)(14.6 \mathrm{~s}) \\ & =-143 \mathrm{~m} / \mathrm{s} \\ v & =\sqrt{v_x^2+v_y^2}\end{aligned}\)
Conceptual Example 5
I Shot a Bullet into the Air…
Suppose you are driving a convertible with the top down. The car is moving to the right at constant velocity. You point a rifle straight up into the air and fire it. In the absence of air resistance, where would the bullet land – behind you, ahead of you, or in the barrel of the rifle?
Example 6 The Height of a Kickoff
A placekicker kicks a football at and angle of 40.0 degrees and the initial speed of the ball is \(22 \mathrm{~m} / \mathrm{s}\). Ignoring air resistance, determine the maximum height that the ball attains.
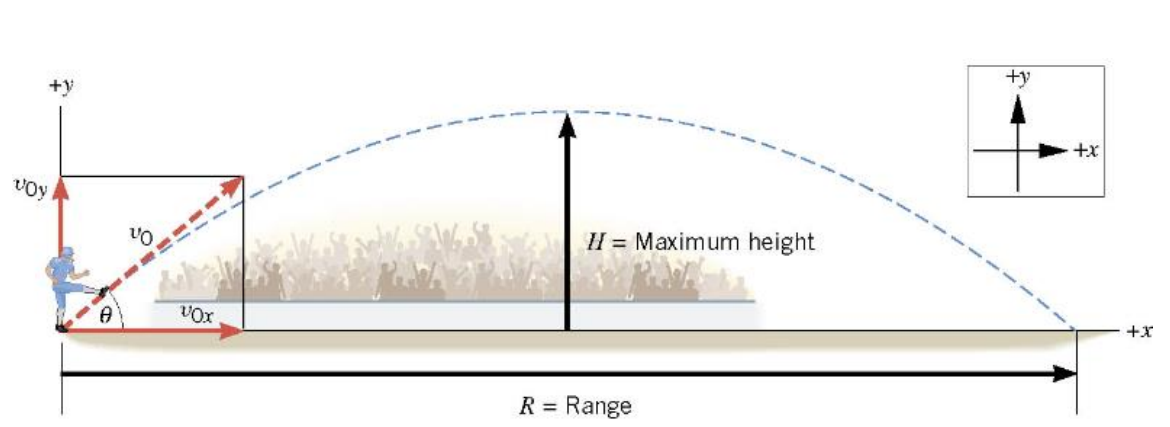
\(\begin{gathered}v_{o y}=v_o \sin \theta=(22 \mathrm{~m} / \mathrm{s}) \sin 40^{\circ}=14 \mathrm{~m} / \mathrm{s} \\ v_{o x}=v_o \sin \theta=(22 \mathrm{~m} / \mathrm{s}) \cos 40^{\circ}=17 \mathrm{~m} / \mathrm{s}\end{gathered}\)



\(v_y^2=v_{o y}^2+2 a_y y\)
\(y=\frac{v_y^2-v_{o y}^2}{2 a_y}\)
\(y=\frac{0-(14 \mathrm{~m} / \mathrm{s})^2}{2\left(-9.8 \mathrm{~m} / \mathrm{s}^2\right)}=+10 \mathrm{~m}\)
Example 7
The Time of Flight of a Kickoff What is the time of flight between kickoff and landing?
▶️Answer/Explanation




\(\begin{gathered}y=v_{o y} t+\frac{1}{2} a_y t^2 \\ 0=(14 \mathrm{~m} / \mathrm{s}) t+\frac{1}{2}\left(-9.80 \mathrm{~m} / \mathrm{s}^2\right) t^2 \\ 0=2(14 \mathrm{~m} / \mathrm{s})+\left(-9.80 \mathrm{~m} / \mathrm{s}^2\right) t \\ t=0, \quad t=2.9 \mathrm{~s}\end{gathered}\)
Example 8
The Range of a Kickoff Calculate the range \(\mathrm{R}\) of the projectile.
▶️Answer/Explanation

\(\begin{aligned} & x=v_{o x} t+\frac{1}{2} a_x t^2=v_{o x} t \\ & =(17 \mathrm{~m} / \mathrm{s})(2.9 \mathrm{~s})=+49 \mathrm{~m}\end{aligned}\)
Conceptual Example 10
Two Ways to Throw a Stone
From the top of a cliff, a person throws two stones. The stones have identical initial speeds, but stone 1 is thrown downward at some angle above the horizontal and stone 2 is thrown at the same angle below the horizontal. Neglecting air resistance, which stone, if either, strikes the water with greater velocity?

The Effects of the Air
We have assumed that the air through which the projectile moves has no effect on its motion. However, in many situations, the disagreement between our calculations
and the actual motion of the projectile can be large because the air resists (opposes) the motion.
for example, in graph below , shows two paths for a fly ball that leaves the bat at an angle of 60° with the horizontal and an initial speed of 44.7 m/s. Path I (the baseball player’s fly ball) is a calculated path that approximates normal conditions of play, in air. Path II (the physics professor’s fly ball) is the path the ball would follow in a vacuum.

(I) The path of a fly ball calculated by taking air resistance into account.
(II) The path the ball would follow in a vacuum,
Hence Air Resistance reduces both Maximum Height and Range.