- IB DP Physics 2025 SL- IB Style Practice Questions with Answer-Topic Wise-Paper 1
- IB DP Physics 2025 HL- IB Style Practice Questions with Answer-Topic Wise-Paper 1
- IB DP Physics 2025 SL- IB Style Practice Questions with Answer-Topic Wise-Paper 2
- IB DP Physics 2025 HL- IB Style Practice Questions with Answer-Topic Wise-Paper 2
5.1 Uniform Circular Motion
DEFINITION OF UNIFORM CIRCULAR MOTION
Uniform circular motion is the motion of an object traveling at a constant speed on a circular path.
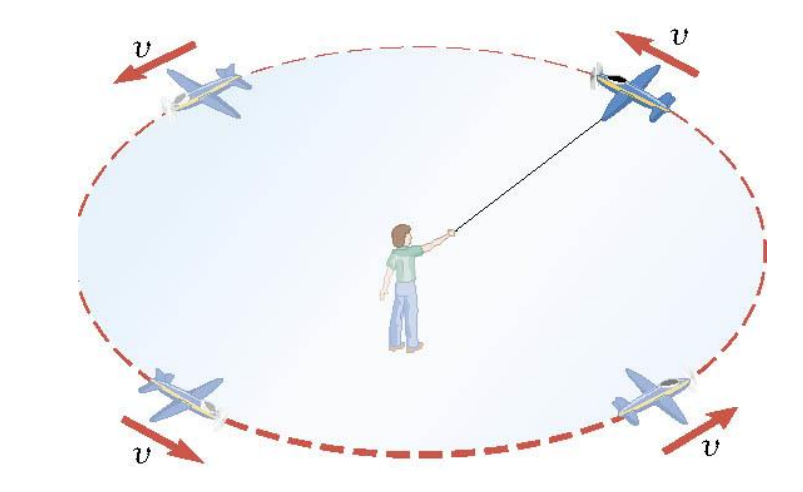
Let \(T\) be the time it takes for the object to travel once around the circle.
$
v=\frac{2 \pi r}{T}
$

Example 1:
A Tire-Balancing Machine
The wheel of a car has a radius of \(0.29 \mathrm{~m}\) and it being rotated at 830 revolutions per minute on a tire-balancing machine. Determine the speed at which the outer edge of the wheel is moving.
▶️Answer/Explanation
$
\begin{gathered}
\frac{1}{830 \text { revolutions } / \mathrm{min}}=1.2 \times 10^{-3} \mathrm{~min} / \text { revolution } \\
T=1.2 \times 10^{-3} \mathrm{~min}=0.072 \mathrm{~s} \\
v=\frac{2 \pi r}{T}=\frac{2 \pi(0.29 \mathrm{~m})}{0.072 \mathrm{~s}}=25 \mathrm{~m} / \mathrm{s}
\end{gathered}
$
In uniform circular motion, the speed is constant, but the direction of the velocity vector is not constant.

\(\begin{aligned} & \alpha+\beta=90^{\circ} \\ & \alpha+\theta=90^{\circ}\end{aligned}\)
\(\begin{aligned} & \alpha+\beta=90^{\circ} \\ & \alpha+\theta=90^{\circ}\end{aligned}\)
\(\beta=\theta\)

\(\frac{\Delta v}{v}=\frac{v \Delta t}{r}\)
\(\frac{\Delta v}{\Delta t}=\frac{v^2}{r}\)
\(a_c=\frac{v^2}{r}\)
5.2 Centripetal Acceleration
The direction of the centripetal acceleration is towards the center of the circle; in the same direction as the change in velocity.
\(a_c=\frac{v^2}{r}\)

Conceptual Example 2: Which Way Will the Object Go?
An object is in uniform circular motion. At point \(O\) it is released from its circular path. Does the object move along the straight path between \(O\) and \(A\) or along the circular arc between points \(O\) and \(P\) ?
▶️Answer/Explanation

Example 3: The Effect of Radius on Centripetal Acceleration

The bobsled track contains turns with radii of \(33 \mathrm{~m}\) and \(24 \mathrm{~m}\). Find the centripetal acceleration at each turn for a speed of \(34 \mathrm{~m} / \mathrm{s}\). Express answers as multiples of \(g=9.8 \mathrm{~m} / \mathrm{s}^2\).
\(a_c=v^2 / r\)
\(a_c=\frac{(34 \mathrm{~m} / \mathrm{s})^2}{33 \mathrm{~m}}=35 \mathrm{~m} / \mathrm{s}^2=3.6 \mathrm{~g}\)

\(a_c=\frac{(34 \mathrm{~m} / \mathrm{s})^2}{24 \mathrm{~m}}=48 \mathrm{~m} / \mathrm{s}^2=4.9 \mathrm{~g}\)
5.3 Centripetal Force
Recall Newton’s Second Law
When a net external force acts on an object of mass \(m\), the acceleration that results is directly proportional to the net force and has a magnitude that is inversely proportional to the mass. The direction of the acceleration is the same as the direction of the net force.
\(\overrightarrow{\mathbf{a}}=\frac{\sum \overrightarrow{\mathbf{F}}}{m} \quad \sum \overrightarrow{\mathbf{F}}=m \overrightarrow{\mathbf{a}}\)
Thus, in uniform circular motion there must be a net force to produce the centripetal acceleration.
The centripetal force is the name given to the net force required to keep an object moving on a circular path.
The direction of the centripetal force always points toward the center of the circle and continually changes direction as the object moves.
$
F_c=m a_c=m \frac{v^2}{r}
$
Example 5: The Effect of Speed on Centripetal Force
The model airplane has a mass of \(0.90 \mathrm{~kg}\) and moves at constant speed on a circle that is parallel to the ground. The path of the airplane and the guideline lie in the same horizontal plane because the weight of the plane is balanced by the lift generated by its wings. Find the tension in the \(17 \mathrm{~m}\) guideline for a speed of \(19 \mathrm{~m} / \mathrm{s}\).

\(\begin{aligned} & F_c=T=m \frac{v^2}{r} \\ & T=(0.90 \mathrm{~kg}) \frac{(19 \mathrm{~m} / \mathrm{s})^2}{17 \mathrm{~m}}=19 \mathrm{~N}\end{aligned}\)
Conceptual Example 6: A Trapeze Act
In a circus, a man hangs upside down from a trapeze, legs bent over and arms downward, holding his partner. Is it harder for the man to hold his partner when the partner hangs straight down and is stationary of when the partner is swinging through the straight-down position?
▶️Answer/Explanation

5.4 Banked Curves
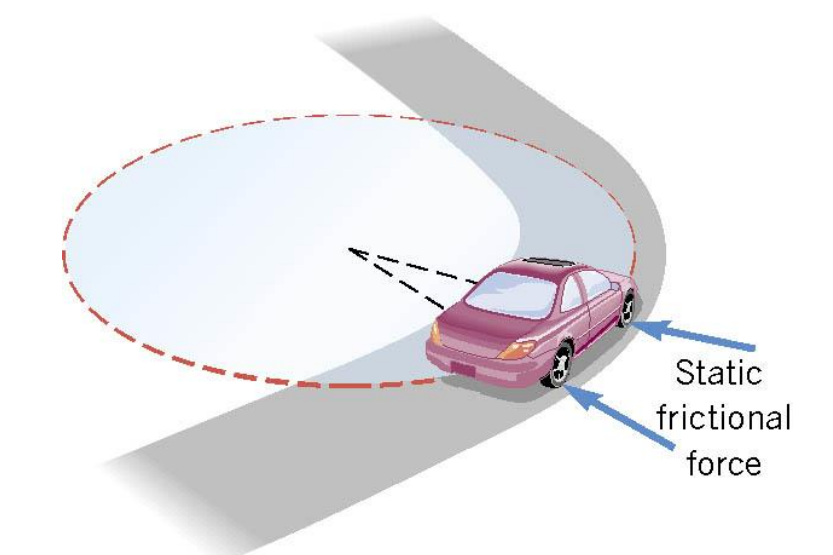
On an unbanked curve, the static frictional force provides the centripetal force.
On a frictionless banked curve, the centripetal force is the horizontal component of the normal force. The vertical component of the normal force balances the car’s weight.

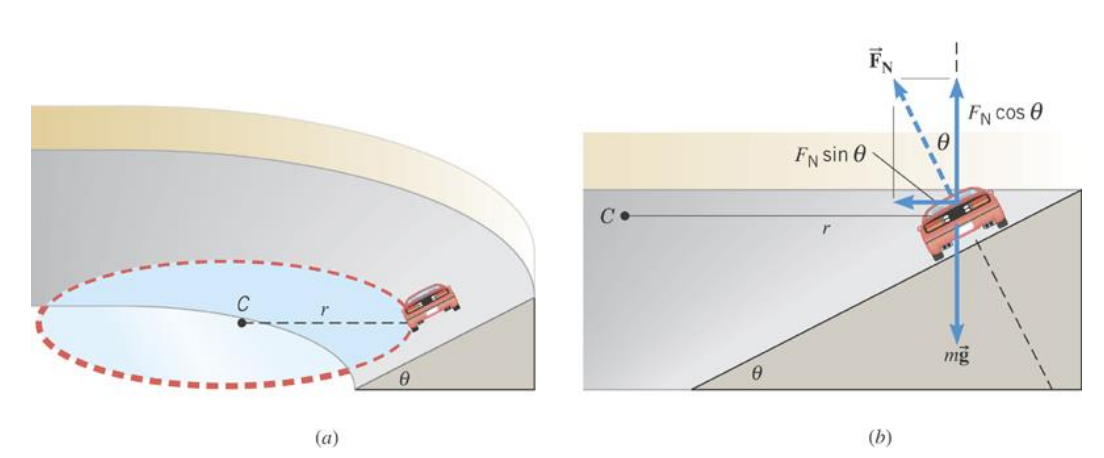
\(F_c=F_N \sin \theta=m \frac{v^2}{r}\)
\(\begin{aligned} & F_N \sin \theta=m \frac{v^2}{r} \\ & F_N \cos \theta=m g\end{aligned}\)
\(F_N \cos \theta=m g\)
\(\tan \theta=\frac{v^2}{r g}\)

Example 8: The Daytona 500
The turns at the Daytona International Speedway have a maximum radius of \(316 \mathrm{~m}\) and are steeply banked at 31 degrees. Suppose these turns were frictionless. At what speed would the cars have to travel around them in order to remain on the track?
▶️Answer/Explanation
$
\begin{aligned}
\tan \theta & =\frac{v^2}{r g} \longmapsto v=\sqrt{r g \tan \theta} \\
v & =\sqrt{(316 \mathrm{~m})\left(9.8 \mathrm{~m} / \mathrm{s}^2\right) \tan 31^{\circ}}=43 \mathrm{~m} / \mathrm{s}(96 \mathrm{mph})
\end{aligned}
$
5.5 Satellites in Circular Orbits
There is only one speed that a satellite can have if the satellite is to remain in an orbit with a fixed radius.


\(F_c=G \frac{m M_E}{r^2}=m \frac{v^2}{r}\)
\(v=\sqrt{\frac{G M_E}{r}}\)
Example 9: Orbital Speed of the Hubble Space Telescope
Determine the speed of the Hubble Space Telescope orbiting at a height of \(598 \mathrm{~km}\) above the earth’s surface.
▶️Answer/Explanation
$
\begin{aligned}
& v=\sqrt{\frac{\left(6.67 \times 10^{-11} \mathrm{~N} \cdot \mathrm{m}^2 / \mathrm{kg}^2\right)\left(5.98 \times 10^{24} \mathrm{~kg}\right)}{6.38 \times 10^6 \mathrm{~m}+598 \times 10^3 \mathrm{~m}}} \\
& =7.56 \times 10^3 \mathrm{~m} / \mathrm{s} \quad(16900 \mathrm{mi} / \mathrm{h})
\end{aligned}
$
\(v=\sqrt{\frac{G M_E}{r}}=\frac{2 \pi r}{T}\)
\(T=\frac{2 \pi r^{3 / 2}}{\sqrt{G M_E}}\)
Global Positioning System
$
T=24 \text { hours } \quad T=\frac{2 \pi r^{3 / 2}}{\sqrt{G M_E}}
$

5.6 Apparent Weightlessness and Artificial Gravity
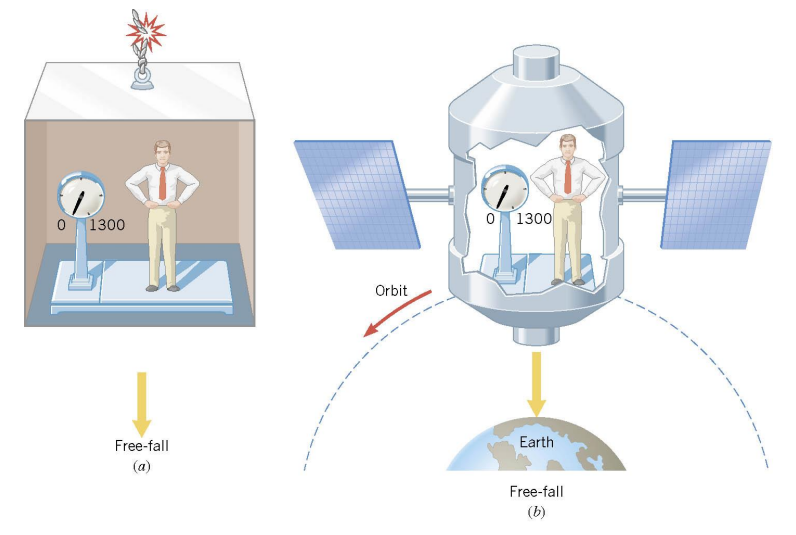
Conceptual Example 12: Apparent Weightlessness and Free Fall
In each case, what is the weight recorded by the scale?
Example 13: Artificial Gravity

\(\begin{aligned} & F_c=m \frac{v^2}{r}=m g \\ v & =\sqrt{r g} \\ = & \sqrt{(1700 \mathrm{~m})\left(9.80 \mathrm{~m} / \mathrm{s}^2\right)} \\ = & 130 \mathrm{~m} / \mathrm{s}\end{aligned}\)
5.7 Vertical Circular Motion

\(\begin{aligned} & F_{N 1}-m g=m \frac{v_1^2}{r} \\ & F_{N 2}=m \frac{v_2^2}{r} \\ & F_{N 4}=m \frac{v_4^2}{r} \\ & F_{N 3}+m g=m \frac{v_3^2}{r}\end{aligned}\)
At what speed must the surface of the space station move so that the astronaut experiences a push on his feet equal to his weight on earth? The radius is \(1700 \mathrm{~m}\).