- IB DP Physics 2025 SL- IB Style Practice Questions with Answer-Topic Wise-Paper 1
- IB DP Physics 2025 HL- IB Style Practice Questions with Answer-Topic Wise-Paper 1
- IB DP Physics 2025 SL- IB Style Practice Questions with Answer-Topic Wise-Paper 2
- IB DP Physics 2025 HL- IB Style Practice Questions with Answer-Topic Wise-Paper 2
4.1 The Concepts of Force and Mass
A force is a push or a pull.
Contact forces arise from physical contact .
Action-at-a-distance forces do not require contact and include gravity and electrical forces.
Arrows are used to represent forces. The length of the arrow is proportional to the magnitude of the force.

Mass is a measure of the amount of “stuff” contained in an object.
4.2 Newton’s First Law of Motion
Newton’s First Law
An object continues in a state of rest or in a state of motion at a constant speed along a straight line, unless compelled to change that state by a net force.
The net force is the vector sum of all of the forces acting on an object.
The net force on an object is the vector sum of all forces acting on that object.
The SI unit of force is the Newton (N).


Inertia is the natural tendency of an object to remain at rest or in motion at a constant speed along a straight line.
The mass of an object is a quantitative measure of inertia.
SI Unit of Mass: kilogram (kg)
An inertial reference frame is one in which Newton’s Law of Inertia is valid.
All accelerating reference frames are noninertial.
4.3 Newton’s Second Law of Motion
Mathematically, the net force is written as
$
\sum \overrightarrow{\mathbf{F}}
$
where the Greek letter sigma denotes the vector sum.
Newton’s Second Law
When a net external force acts on an object of mass \(m\), the acceleration that results is directly proportional to the net force and has a magnitude that is inversely proportional to the mass. The direction of the acceleration is the same as the direction of the net force.
$
\overrightarrow{\mathbf{a}}=\frac{\sum \overrightarrow{\mathbf{F}}}{m} \quad \sum \overrightarrow{\mathbf{F}}=m \overrightarrow{\mathbf{a}}
$
SI Unit for Force
$
(\mathrm{kg})\left(\frac{\mathrm{m}}{\mathrm{s}^2}\right)=\frac{\mathrm{kg} \cdot \mathrm{m}}{\mathrm{s}^2}
$
This combination of units is called a newton \((\mathrm{N})\).

A free-body-diagram is a diagram that represents the object and the forces that act on it.


The net force in this case is:
$
275 N+395 N-560 N=+110 N
$
and is directed along the \(+x\) axis of the coordinate system.
If the mass of the car is \(1850 \mathrm{~kg}\) then, by Newton’s second law, the acceleration is
$
a=\frac{\sum F}{m}=\frac{+110 \mathrm{~N}}{1850 \mathrm{~kg}}=+0.059 \mathrm{~m} / \mathrm{s}^2
$
4.4 The Vector Nature of Newton’s Second Law
The direction of force and acceleration vectors can be taken into account by using \(x\) and \(y\) components.
$
\sum \overrightarrow{\mathbf{F}}=m \overrightarrow{\mathbf{a}}
$
is equivalent to
\(\sum F_y=m a_y \quad \sum F_x=m a_x\)

The net force on the raft can be calculated in the following way:

\(\begin{aligned} & a_x=\frac{\sum F_x}{m}=\frac{+23 \mathrm{~N}}{1300 \mathrm{~kg}}=+0.018 \mathrm{~m} / \mathrm{s}^2 \\ & a_y=\frac{\sum F_y}{m}=\frac{+14 \mathrm{~N}}{1300 \mathrm{~kg}}=+0.011 \mathrm{~m} / \mathrm{s}^2\end{aligned}\)
4.5 Newton’s Third Law of Motion
Newton’s Third Law of Motion
Whenever one body exerts a force on a second body, the second body exerts an oppositely directed force of equal magnitude on the first body.

Suppose that the magnitude of the force is \(36 \mathrm{~N}\). If the mass of the spacecraft is \(11,000 \mathrm{~kg}\) and the mass of the astronaut is \(92 \mathrm{~kg}\), what are the accelerations?
On thespacecraft \(\sum \overrightarrow{\mathbf{F}}=\overrightarrow{\mathbf{P}}\).
On the astronaut \(\sum \overrightarrow{\mathbf{F}}=-\overrightarrow{\mathbf{P}}\).
$
\overrightarrow{\mathbf{a}}_s=\frac{\overrightarrow{\mathbf{P}}}{m_s}=\frac{+36 \mathrm{~N}}{11,000 \mathrm{~kg}}=+0.0033 \mathrm{~m} / \mathrm{s}^2
$
\(\overrightarrow{\mathbf{a}}_A=\frac{-\overrightarrow{\mathbf{P}}}{m_A}=\frac{-36 \mathrm{~N}}{92 \mathrm{~kg}}=-0.39 \mathrm{~m} / \mathrm{s}^2\)
4.6 Types of Forces: An Overview
In nature there are two general types of forces, fundamental and nonfundamental.
Fundamental Forces
1. Gravitational force
2. Strong Nuclear force
3. Electroweak force
Examples of nonfundamental forces:
friction
tension in a rope
normal or support forces
Newton’s Law of Universal Gravitation
Every particle in the universe exerts an attractive force on every other particle.
A particle is a piece of matter, small enough in size to be regarded as a mathematical point.
The force that each exerts on the other is directed along the line joining the particles.
For two particles that have masses \(m_1\) and \(m_2\) and are separated by a distance \(r\), the force has a magnitude given by
$
\begin{gathered}
F=G \frac{m_1 m_2}{r^2} \\
G=6.673 \times 10^{-11} \mathrm{~N} \cdot \mathrm{m}^2 / \mathrm{kg}^2
\end{gathered}
$


\(\begin{aligned} & F=G \frac{m_1 m_2}{r^2} \\ & =\left(6.67 \times 10^{-11} \mathrm{~N} \cdot \mathrm{m}^2 / \mathrm{kg}^2\right) \frac{(12 \mathrm{~kg})(25 \mathrm{~kg})}{(1.2 \mathrm{~m})^2} \\ & =1.4 \times 10^{-8} \mathrm{~N}\end{aligned}\)

Definition of Weight
The weight of an object on or above the earth is the gravitational force that the earth exerts on the object. The weight always acts downwards, toward the center of the earth.
On or above another astronomical body, the weight is the gravitational force exerted on the object by that body.
SI Unit of Weight: newton (N)
Relation Between Mass and Weight

\(\begin{gathered}W=G \frac{M_E m}{r^2} \\ W=m g \\ g=G \frac{M_E}{r^2}\end{gathered}\)
On the earth’s surface:
$
\begin{aligned}
& g=G \frac{M_E}{R_E^2} \\
& =\left(6.67 \times 10^{-11} \mathrm{~N} \cdot \mathrm{m}^2 / \mathrm{kg}^2\right) \frac{\left(5.98 \times 10^{24} \mathrm{~kg}\right)}{\left(6.38 \times 10^6 \mathrm{~m}\right)^2} \\
& =9.80 \mathrm{~m} / \mathrm{s}^2
\end{aligned}
$
4.8 The Normal Force
Definition of the Normal Force
The normal force is one component of the force that a surface exerts on an object with which it is in contact – namely, the component that is perpendicular to the surface.

\(\begin{aligned} & F_N-11 \mathrm{~N}-15 \mathrm{~N}=0 \\ & F_N=26 \mathrm{~N}\end{aligned}\)
\(\begin{aligned} & F_N+11 \mathrm{~N}-15 \mathrm{~N}=0 \\ & F_N=4 \mathrm{~N}\end{aligned}\)

Apparent Weight
The apparent weight of an object is the reading of the scale. It is equal to the normal force the man exerts on the scale.


\(\sum F_y=+F_N-m g=m a\)

4.9 Static and Kinetic Frictional Forces
When an object is in contact with a surface there is a force acting on that object. The component of this force that is parallel to the surface is called the frictional force.

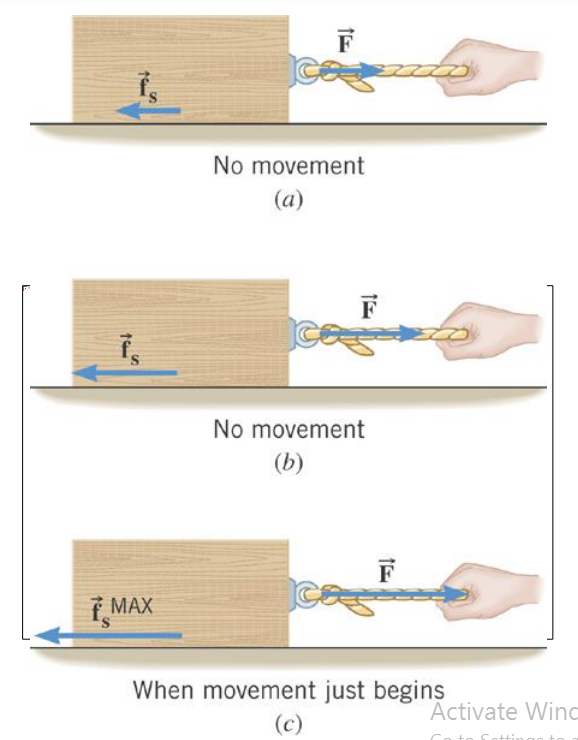
When the two surfaces are not sliding across one another the friction is called static friction.
The magnitude of the static frictional force can have any value from zero up to a maximum value.
$
\begin{gathered}
f_s \leq f_s^{M A X} \\
f_s^{M A X}=\mu_s F_N
\end{gathered}
$
\(0 \leq \mu_s \quad\) is called the coefficient of static friction.
Note that the magnitude of the frictional force does not depend on the contact area of the surfaces.

Static friction opposes the impending relative motion between two objects.
Kinetic friction opposes the relative sliding motion motions that actually does occur.
\(f_k=\mu_k F_N\)
\(0 \leq \mu_k \quad\) is called the coefficient of kinetic friction
Table 4.2 Approximate Values of the Coefficients of Friction for Various Surfaces*
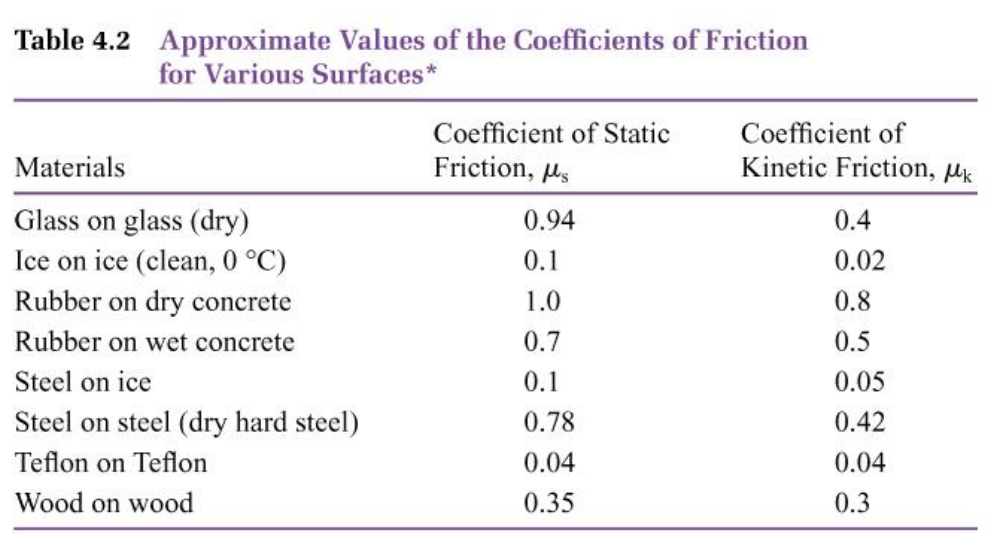
*The last column gives the coefficients of kinetic friction, a concept that will be discussed shortly.
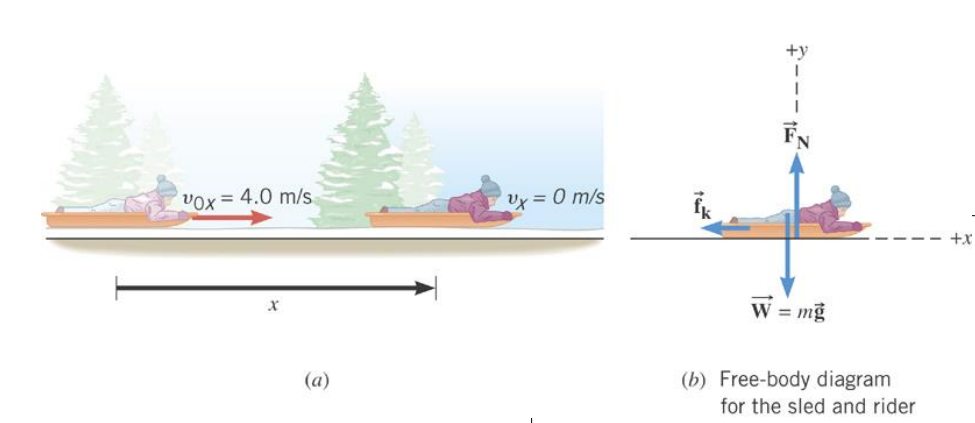
The sled comes to a halt because the kinetic frictional force opposes its motion and causes the sled to slow down.

Suppose the coefficient of kinetic friction is 0.05 and the total mass is \(40 \mathrm{~kg}\). What is the kinetic frictional force?
\(\begin{aligned} & f_k=\mu_k F_N=\mu_k m g= \\ & 0.05(40 \mathrm{~kg})\left(9.80 \mathrm{~m} / \mathrm{s}^2\right)=20 \mathrm{~N}\end{aligned}\)
4.10 The Tension Force
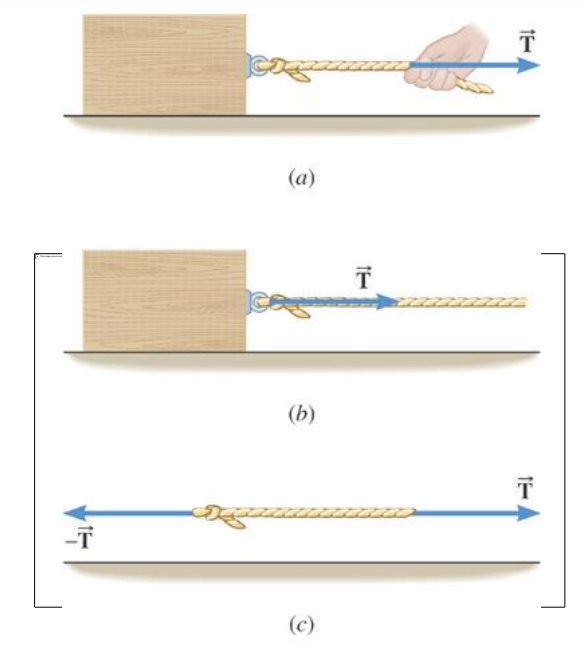
Cables and ropes transmitforces through tension.

A massless rope will transmit tension undiminished from one end to the other.
If the rope passes around a massless, frictionless pulley, the tension will be transmitted to the other end of the rope undiminished.
4.11 Equilibrium Application of Newton’s Laws of Motion
Definition of Equilibrium
An object is in equilibrium when it has zero acceleration.
\(\begin{aligned} & \sum F_x=0 \\ & \sum F_y=0\end{aligned}\)
Reasoning Strategy
- Select an object(s) to which the equations of equilibrium are to be applied.
- Draw a free-body diagram for each object chosen above. Include only forces acting on the object, not forces the object exerts on its environment.
- Choose a set of \(x, y\) axes for each object and resolve all forces in the free-body diagram into components that point along these axes.
- Apply the equations and solve for the unknown quantities.

\(\begin{gathered}+T_1 \sin 35^{\circ}-T_2 \sin 35^{\circ}=0 \\ +T_1 \cos 35^{\circ}+T_2 \cos 35^{\circ}-F=0\end{gathered}\)


$
\begin{gathered}
\sum F_x=-T_1 \sin 10.0^{\circ}+T_2 \sin 80.0^{\circ}=0 \\
\sum F_y=+T_1 \cos 10.0^{\circ}-T_2 \cos 80.0^{\circ}-W=0
\end{gathered}
$
The first equation gives \(T_1=\left(\frac{\sin 80.0^{\circ}}{\sin 10.0^{\circ}}\right) T_2\)
Substitution into the second gives
$
\left(\frac{\sin 80.0^{\circ}}{\sin 10.0^{\circ}}\right) T_2 \cos 10.0^{\circ}-T_2 \cos 80.0^{\circ}-W=0
$
\(T_2=\frac{W}{\left(\frac{\sin 80.0^{\circ}}{\sin 10.0^{\circ}}\right) \cos 10.0^{\circ}-\cos 80.0^{\circ}}\)
\(T_2=582 \mathrm{~N} \quad T_1=3.30 \times 10^3 \mathrm{~N}\)
4.12 Nonequilibrium Application of Newton’s Laws of Motion
When an object is accelerating, it is not in equilibrium.
$
\begin{aligned}
& \sum F_x=m a_x \\
& \sum F_y=m a_y
\end{aligned}
$

The acceleration is along the \(x\) axis so \(\quad a_y=0\)

\(\begin{aligned} & \sum F_y=+T_1 \sin 30.0^{\circ}-T_2 \sin 30.0=0 \\ & \Rightarrow T_1=T_2\end{aligned}\)
\(\begin{aligned} & \sum F_x=+T_1 \cos 30.0^{\circ}+T_2 \cos 30.0+D-R \\ & \quad=m a_x \\ & \left(\text { mass }=1.50 \times 10^8 \mathrm{~kg}\right)\end{aligned}\)
\(\begin{gathered}T_1=T_2=T \\ T=\frac{m a_x+R-D}{2 \cos 30.0^{\circ}}=1.53 \times 10^5 \mathrm{~N}\end{gathered}\)