Class 12th Physics Chapter Wise notes on Nuclei are available in this article. These notes are based on latest CBSE Class 12 Physics Syllabus and important for coming CBSE board exam .
The topics covered in these notes are given below
| Atomic Masses |
| Discovery of Neutron |
| Basic Properties of Neutron |
| Composition of Nucleus |
| Size of the Nucleus |
| Nuclear Density |
| Mass – Energy Equivalence |
| Size of the Nucleus |
| Isotopes |
| Isobars |
| Isotones |
| Energy Equivalence of One Atomic Mass Unit |
| Nuclear binding energy |
| Mass Defect |
| Binding Energy |
| Binding Energy per Nucleon |
| Binding Energy Curve and its Features |
| Nuclear Force |
The notes of the chapter are given below
Atomic Masses
The mass of an atom is extremely small. It means the mass of a carbon atom 12C is about 1.99 × 10‒26 kg. So, kilogram is not a convenient unit to measure such small mass. A different mass unit (atomic mass unit) is used for expressing atomic masses this is known as atomic mass unit.
This unit is the atomic mass unit (u), defined as 1/12th of the mass of carbon (12C) atom.
1 a.m.u. = 1.66 × 10‒27 kg
Discovery of Neutron
In 1932 by James Chadwick observed emission of neutral radiation when beryllium nuclei were bombarded with alpha-particles (or helium nuclei).
It was found that this neutral radiation could knock out protons from light nuclei such as those of helium, carbon and nitrogen. The only neutral radiation known at that time was photons (electromagnetic radiation).
Application of the principles of conservation of energy and momentum showed that if the neutral radiation consisted of photons, the energy of photons would have to be much higher than is available from the bombardment of beryllium nuclei with α-particles.
This phenomenon can be explained by assuming that the neutral radiation consists of a new type of neutral particles called neutrons.
Basic Properties of Neutron
• mn = 1.00866 u = 1.6749 × 10‒27 kg
• A free neutron, unlike a free proton, is unstable.
• It decays into a proton, an electron and a antineutrino (another elementary particle), and has a mean life of about 1000s. It is, however, stable inside the nucleus.
Composition of Nucleus
The composition of a nucleus can now be described using the following terms and symbols:
Z – atomic number = number of protons
N – neutron number = number of neutrons
A – mass number = Z + N = total number of protons and neutrons
One also uses the term nucleon for a proton or a neutron.
Number of nucleons in an atom is its mass number A.
Nuclear species or nuclides are shown by the notation where X is the chemical symbol of the species.
For example, the nucleus of gold is denoted by It contains 197 nucleons, of which 79 are protons and the rest 118 are neutrons.
Size of the Nucleus
It has been found that a nucleus of mass number A has a radius R = Ro A1/3
Where, Ro = 1.2 × 10‒15 m.
This means the volume of the nucleus, which is proportional to R3 is proportional to A.
Nuclear Density
The density of nucleus is a constant, independent of A, for all nuclei. The density of nuclear matter is approximately 2.3 × 1017 kg m–3.
Mass – Energy Equivalence
Einstein showed from his theory of special relativity that it is necessary to treat mass as another form of energy.
Einstein gave the famous mass-energy equivalence relation E = m c2.
Here the energy equivalent of mass m is related by the above equation and c is the velocity of light in vacuum and is approximately equal to 3×108 m s–1.
Size of the Nucleus
By performing scattering experiments in which fast electrons, instead of α-particles, are projectiles that bombard targets made up of various elements, the sizes of nuclei of various elements have been accurately measured.
It has been found that a nucleus of mass number A has a radius then, R = Ro A1/3
Where Ro = 1.2 × 10–15 m
This means the volume of the nucleus (which is proportional to R3) is proportional to A. So the density of nucleus is a constant and independent of A.
Isotopes
The nuclei of isotopes of a given element contain the same number of protons, but differ from each other in their number of neutrons.
Isobars
All nuclides with same mass number are called isobars.
Isotones
Nuclei of different atom containing same number of neutrons are called isotones.
Energy Equivalence of One Atomic Mass Unit
1 a.m.u. represents the average mass of a nucleon and 1 a.m.u. = 931.25 eV.
Nuclear binding energy
The nucleus is made up of neutrons and protons so, it may be expected that the mass of the nucleus is equal to the total mass of its individual protons and neutrons. However, the nuclear mass is found to be always less than this.
For example, the nucleus of an oxygen atom (16O8) has 8 neutrons and 8 protons
So,
Mass of 8 neutrons = 8 × 1.00866 u,
Mass of 8 protons = 8 × 1.00727 u,
Mass of 8 electrons = 8 × 0.00055 u
Therefore the expected mass of 16O8 nucleus is 8 × 2.01593 u = 16.12744 u
But, the atomic mass of 16O8 found from mass spectroscopy experiments is seen to be 15.99493 u.
Mass Defect
It is the difference between the sum of the masses of protons and neutrons forming a nucleus and actual mass of the nucleus.
Binding Energy
As, some mass disappears in the formation of a nucleus in the form of mass defect. This loss in mass reappears in the form of energy called binding energy.
In other words, binding energy is the energy which should be supplied to the nucleus in order to break it up into its constituent particles.
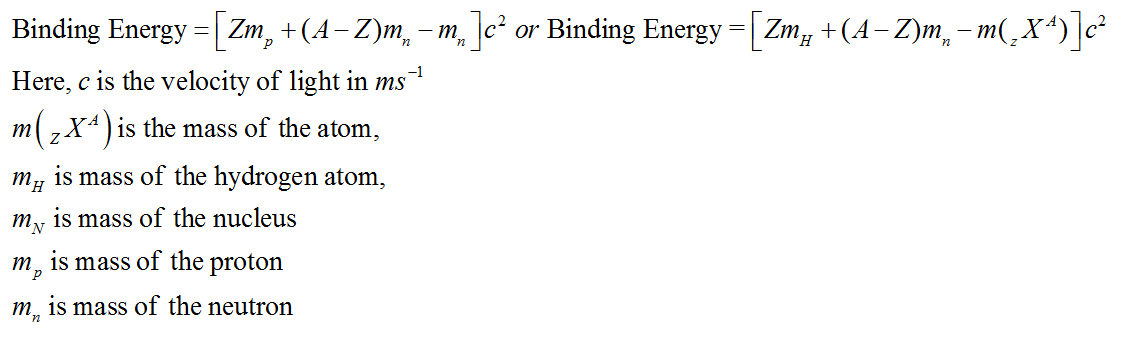
Binding Energy per Nucleon
It is the ratio of the binding energy of a nucleus to the number of the nucleons.
Binding energy per nucleon = (Total binding energy)/(Number of nucleon)
Binding Energy Curve and its Features
Binding energy per nucleon as the average energy per nucleon needed to separate a nucleus into its individual nucleons.
Binding energy curve is a plot of the binding energy per nucleon versus the mass number for large nuclei.
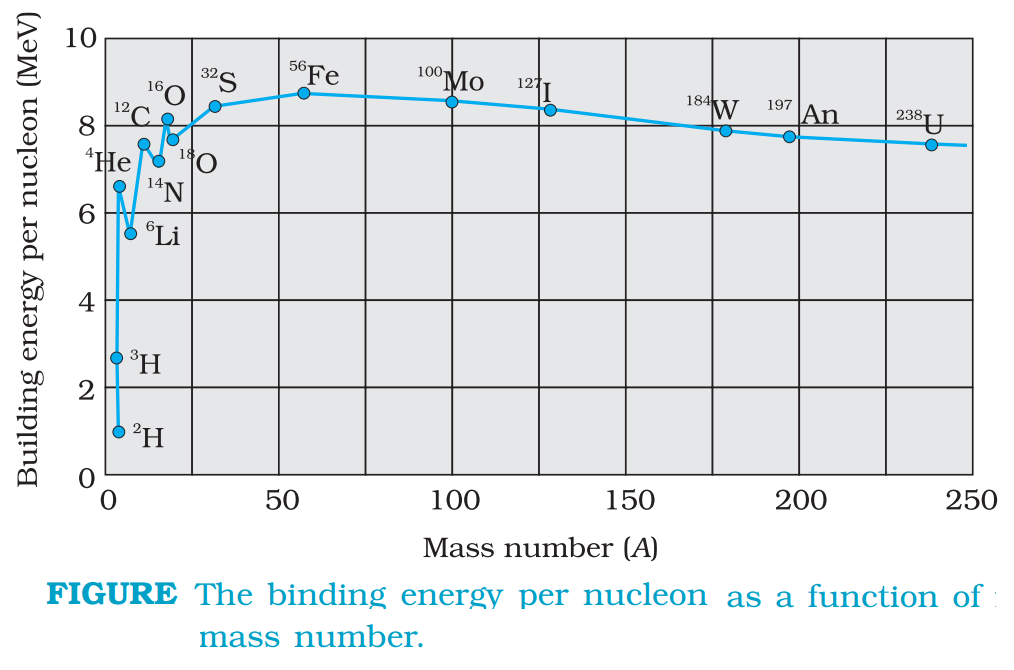
The main features of his curve are give below:
(i) The binding energy per nucleon (Ebn) is practically constant, i.e. practically independent of the atomic number for nuclei of middle mass number ( 30 < A < 170). The curve has a maximum of about 8.75 MeV for A = 56 and has a value of 7.6 MeV for A = 238.
(ii) Binding energy per nucleon is lower for both light nuclei (A<30) and heavy nuclei (A>170).
From above two observations we can draw the conclusions given below:
(a) The force is attractive and sufficiently strong to produce a binding energy of a few MeV per nucleon.
(b) The constancy of the binding energy in the range 30 < A < 170 is a consequence of the fact that the nuclear force is short-ranged.
(c)A very heavy nucleus, say A = 240, has lower binding energy per nucleon compared to that of a nucleus with A = 120. Thus if a nucleus A = 240 breaks into two A = 120 nuclei, nucleons get more tightly bound. This implies energy would be released in the process.
(d) Consider two very light nuclei (A ≤ 10) joining to form a heavier nucleus. The binding energy per nucleon of the fused heavier nuclei is more than the binding energy per nucleon of the lighter nuclei. This means that the final system is more tightly bound than the initial system. Again energy would be released in such a process of fusion. This is the energy source of the sun.
Nuclear Force
Previously, we have studied that for average mass nuclei the binding energy per nucleon is approximately 8 MeV, which is much larger than the binding energy in atoms.
Therefore, to bind a nucleus together there must be a strong attractive force of a totally different kind.
This force is nuclear force (strongest force in nature). It is strong enough to overcome the repulsion between the (positively charged) protons and to bind both protons and neutrons into the tiny nuclear volume.
Some important features of the nuclear binding force are given below:
(i) The nuclear force is much stronger than the Coulomb force acting between charges or the gravitational forces between masses. The nuclear binding force has to dominate over the Coulomb repulsive force between protons inside the nucleus. This happens only because the nuclear force is much stronger than the coulomb force. The gravitational force is much weaker than even Coulomb force.
(ii) The nuclear force between two nucleons falls rapidly to zero as their distance is more than a few femtometres. This leads to saturation of forces in a medium or a large-sized nucleus, which is the reason for the constancy of the binding energy per nucleon. A rough plot of the potential energy between two nucleons as a function of distance is shown in the figure given below. The potential energy is a minimum at a distance r0 of about 0.8 fm. This means that the force is attractive for distances larger than 0.8 fm and repulsive if they are separated by distances less than 0.8 fm.
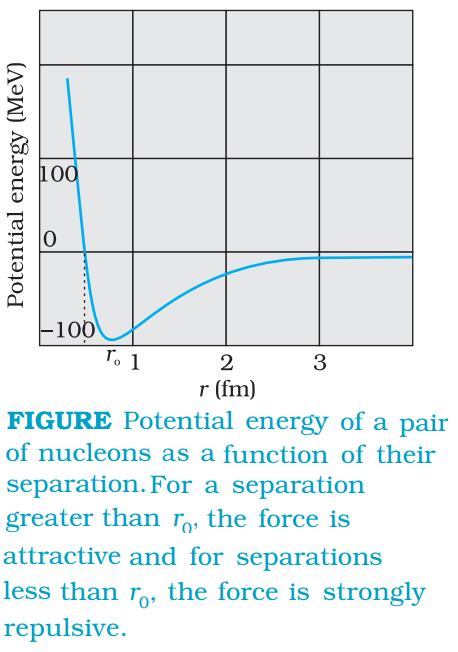
(iii) The nuclear force between neutron-neutron, proton-neutron and proton-proton is approximately the same. The nuclear force does not depend on the electric charge.
In part I, we have studied about following topics: Atomic Masses, Discovery of Neutron, Basic Properties of Neutron, Composition of Nucleus, Size of the Nucleus, Nuclear Density, Mass Defect, Binding Energy, Binding Energy per Nucleon, Binding Energy Curve and its Features etc.
Now, in part II we will study about the topics given below
| Radioactivity |
| Alpha Particles and Alpha Decay |
| Beta Particles and Beta Decay |
| Gamma radiations and Gamma decay |
| Law of Radioactive Decay |
| Radioactive Decay Constant |
| Half Life: Radioactive Substance |
| Relation between Half Life and Decay constant |
| Activity of Radioactive Constant |
| Mean Life (or Average Life) of a Radioactive Substance |
| Units of Radioactive Decay |
| Nuclear Fission |
| Nuclear Fusion |
The notes are given below:
Radioactivity
Radioactivity was discovered by A. H. Becquerel (1986) accidently.
Radioactivity is defined as the spontaneous and continuous disintegration of a nucleus of a heavy element on its own with the emission of certain type of radiations is known as natural radioactivity.
Alpha Particles and Alpha Decay
Alpha particles are helium nuclei of nuclear origin. It carries 2 unit positive charge and its mass is about four times the mass of hydrogen atom.
Phenomenon of emission of an α particles from a nucleus is called alpha decay
Example: 92U238 →90Th234 + 2He4 + Q
Here, Q = (mX ‒ mY ‒ mHe) c2
Generally:
ZXA → z ‒ 2YA ‒ 4 + 2He4 + Q
Beta Particles and Beta Decay
Beta particles are fast moving electrons of nuclear origin. A nucleus that decays spontaneously by emitting an electron or a positron is said to undergo beta decay.
In β‒ decay, an electron an electron is emitted by the nucleus.
Example: 15P32 → 16S32 + e‒ + antineutrino
In β+ decay, a positron is emitted by the nucleus.
Example: 11Na22 → e‒ + Neutrino
In beta-minus decay, a neutron transforms into a proton within the nucleus according to, n → p + e‒ + antineutrino
Whereas in beta-plus decay, a proton transforms into neutron (inside the nucleus) by, p → p + e+ + neutrino
The above processes show that mass number A of a nuclide undergoing beta decay does not change.
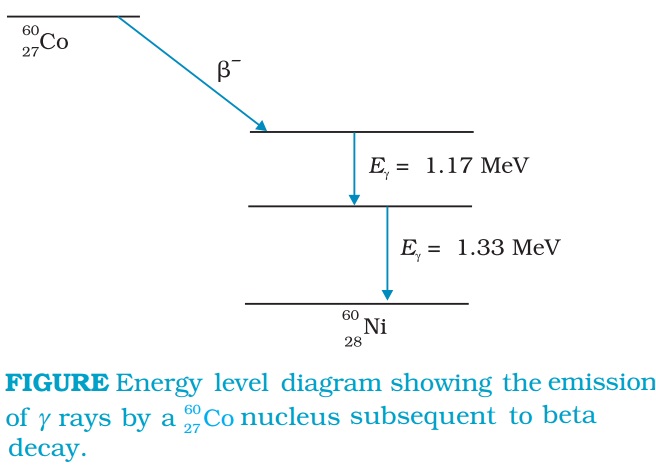
Gamma Radiations and Gamma decay
There are energy levels in a nucleus, just like there are energy levels in atoms. When a nucleus is in an excited state, it can make a transition to a lower energy state by the emission of electromagnetic radiation. As the energy differences between levels in a nucleus are of the order of MeV, the photons emitted by the nuclei have MeV energies and are called gamma rays.
Law of Radioactive Decay
In any radioactive sample, which undergoes α, β or γ-decay, it is found that the number of nuclei undergoing the decay per unit time is proportional to the total number of nuclei in the sample. If N is the number of nuclei in the sample and ΔN undergo decay in time Δt then,
(ΔN/Δt) ∝ N or (ΔN/Δt) = λ N
Where, λ is known as radioactive decay constant or disintegration constant.
Also, N = No e‒λt, here No is the number of radioactive nuclei present initially.
Radioactive Decay Constant
As, N = No e‒λt, now, if we put t = 1/λ, we have, N = No e‒1
⇒ N = No/e
⇒ N = No/2.718
⇒ N =0.368 No
The radioactive decay constant can may be defined as the reciprocal of the time during which the number of atoms is a radioactive substance reduces to 36.8 % of their initial number.
Half Life: Radioactive Substance
It is the time interval in which the mass of a radioactive substance or the number of its atoms is reduced to half of its initial value.
Relation between Half Life and Decay constant
Half life (T1/2) and decay constant (λ) are related as, T1/2 = 0.693/λ
Activity of Radioactive Constant
Rate of disintegration or count rate of a sample of radioactive material is called activity and is directly proportional to the number of atoms of left undecayed in the sample
Activity A, = |dN/dt| = λ N
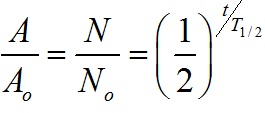
Mean Life (or Average Life) of a Radioactive Substance
It is the average of the lives of all the atoms in a radioactive substance is called the ‘mean life’ or ‘average life’ of that substance.
The mean life (τ) of a radioactive substance is equal to reciprocal of decay constant.
It means, τ = 1/ λ. Also, τ = 1.443 T1/2
Units of Radioactive Decay
Becquerel (Bq) = 1 disintegration per second
Rutherford (rd) = 106 disintegration per second
Curie (Ci) = 3.7 × 1010 disintegration per second
Nuclear Fission
It is the process in which a heavy nucleus splits up into two nuclei of nearly comparable masses.
Example: 92U235 + 1n0 → 92U236 → 36Ba141 + 36Kr92 + 31n0 +Energy
Nuclear Fusion
It is the process in which two or more small nuclei fuse together to form a single heavy nucleus.
The mass of the single heavy nucleus formed is less than the total initial mass of the mass of the parent nuclei.
This difference in mass appears in the form of energy (as per, E = mc2).
Example: 1H2 + 1H2 → 2He4 + Enormous amount of energy
Enormous amount of energy produced by the sun is due to the phenomenon of nuclear fusion.