Magnetism and Matter : Notes and Study Materials -pdf
- Concepts of Magnetism and Matter
- Magnetism and Matter Master File
- Ncert Solution
- NCERT Exemplar Solution
- Important Questions Magnetism And Matter
- Past Many Years CBSE Questions and Answer: Magnetic Dipole
- Past Many Years CBSE Questions and Answer: Magnetic Field
- Past Many Years CBSE Questions and Answer: Magnetic Materials
- Test Paper 1
- Test Paper 2
Origin of Magnetism:
The word magnet is derived from the name of an island in Greece called magnesia where magnetic ore deposits were found, as early as 600 BC. Shepherds on this island complained that their wooden shoes (which had nails) at times stayed struck to the ground. This was the first phenomenon which led to the discovery of magnetism.
Properties of a Magnet
• Attractive property: A magnet attracts magnetic substances like steel, cobalt, iron etc.
• Directive Property: When a bar magnet is freely suspended, it points in the north-south direction. The tip which points to the geographic north is called the north pole and the tip which points to the geographic south is called the south pole of the magnet
• There is a repulsive force when north poles (or south poles) of two magnets are brought close together. Conversely, there is an attractive force between the north pole of one magnet and the south pole of the other.
• We cannot isolate the north, or south pole of a magnet. If a bar magnet is broken into two halves, we get two similar bar magnets with somewhat weaker properties. Unlike electric charges, isolated magnetic north and south poles known as magnetic monopoles do not exist.
Magnetic Field Lines
The magnetic field lines are a visual and intuitive realization of the magnetic field.
Note: Few textbooks refer magnetic field lines as magnetic lines of force. This nomenclature must be avoided as it can be confusing. Unlike electrostatics the field lines in magnetism do not indicate the direction of the force on a (moving) charge.
Properties of Magnetic Field Lines
The magnetic field lines of a magnet (or a solenoid) form continuous closed loops.
The tangent to the field line at a given point represents the direction of the net magnetic field B at that point.
The larger the number of field lines crossing per unit area, the stronger is the magnitude of the magnetic field B.
The magnetic field lines do not intersect, otherwise, the direction of the magnetic field would not be unique at the point of intersection.
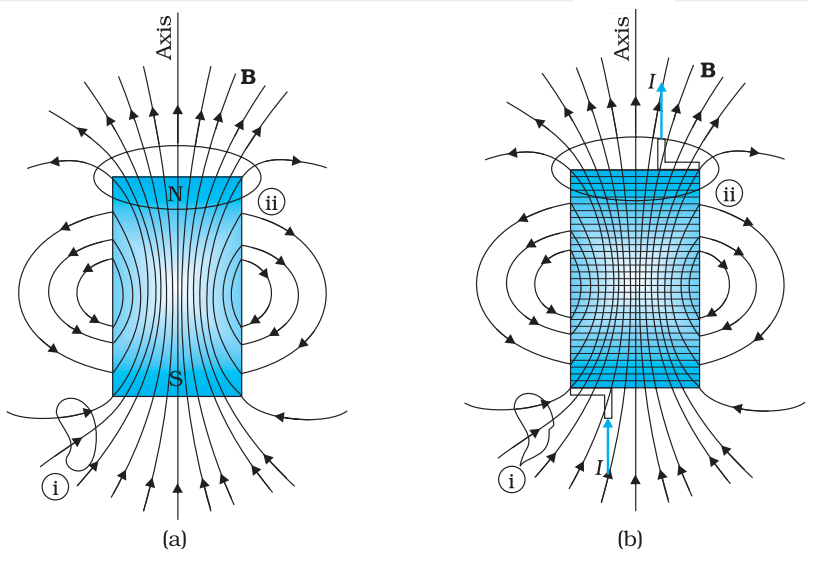
Image Source: NCERT Textbook
Figure (a) shows the magnetic field lines a bar magnet and figure (b) shows magnetic field due to a current-carrying finite solenoid
The larger the number of field lines crossing per unit area, the stronger is the magnitude of the magnetic field B. In figure (a), B is larger around region (ii) than in region (i).
Bar Magnet as an Equivalent Solenoid
The resemblance of magnetic field lines for a bar magnet and a solenoid suggest that a bar magnet may be thought of as a large number of circulating currents in analogy with a solenoid.
One can test this analogy by moving a small compass needle in the neighbourhood of a bar magnet and a current-carrying finite solenoid and noting that the deflections of the needle are similar in both cases.
Cutting a bar magnet in half is like cutting a solenoid. We get two smaller solenoids with weaker magnetic properties.
The field lines remain continuous, emerging from one face of the solenoid and entering into the other face.
Magnetic Dipole & Dipole Moment:
Two unlike poles of equal strength separated by a small distance make a magnetic dipole.
A bar magnet has two magnetic dipoles known as north pole & south pole. The separation between the poles is also known as magnetic length.
Let pole strength of each pole of a magnet be m and its magnetic length is l, then, magnetic dipole moment of a magnet is given by, M = ml
Magnetic dipole moment is a vector quantity and its direction is from south pole of bar magnet to the north pole of bar magnet.
The SI unit of magnetic dipole moment is ampere-meter2.
Magnetic field at a point due to a Bar Magnet
Magnetic field on Axial line or End-on of a short bar magnet:
Magnitude of a magnetic field line of a short bar magnet is given by,
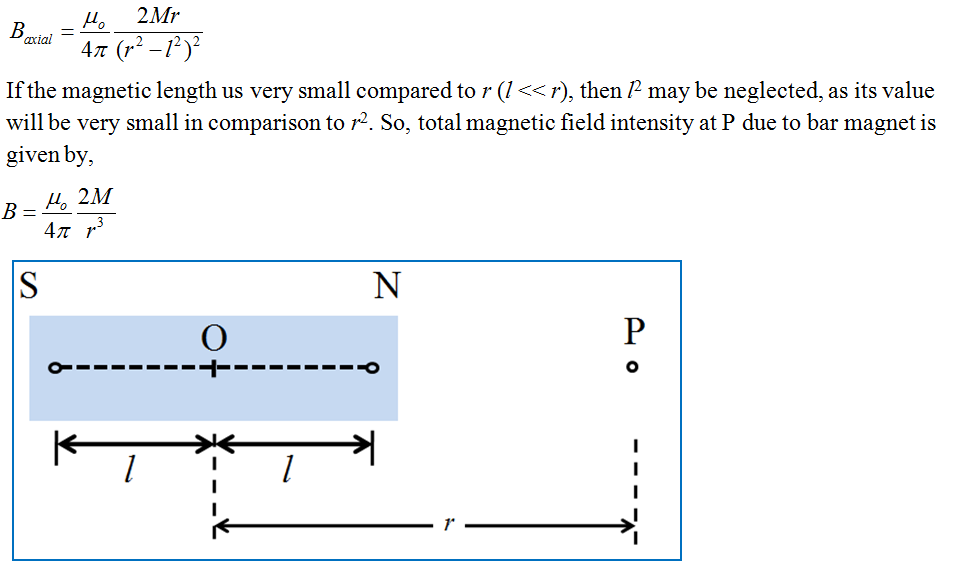
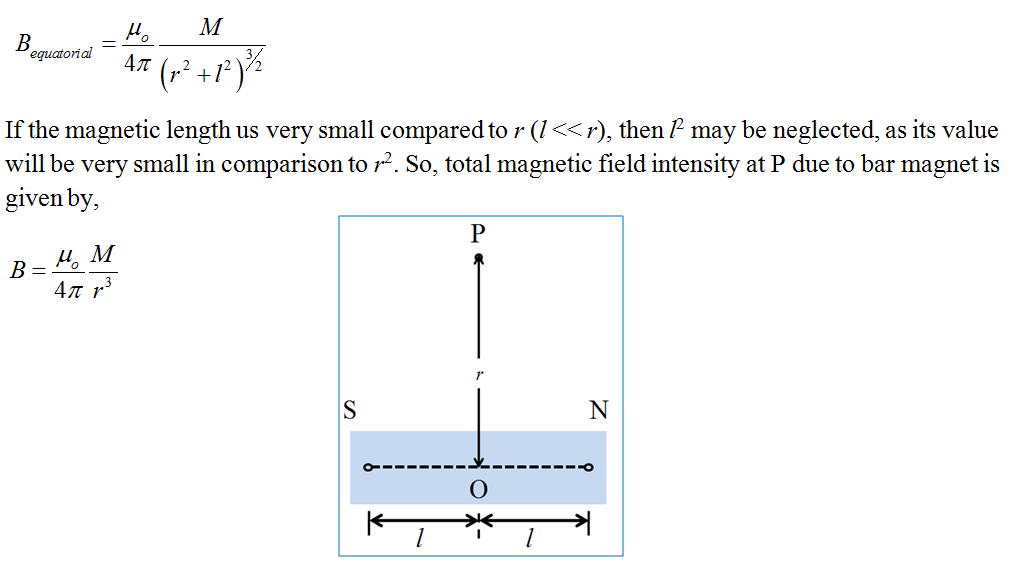
Magnetic field on Equatorial line or Broadside-on of a short bar magnet:
Torque on a Magnetic Dipole in a Uniform Magnetic Field
A magnetic dipole (or a bar magnet) having dipole moment M when placed in a uniform magnetic field B, experiences a torque,
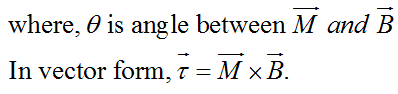
Potential Energy of a Magnetic Dipole in a Uniform Magnetic Field
The magnetic potential energy is given by,
The Electrostatic Analogy
Image Source: NCERT Textbook
Magnetism and Gauss’s Law
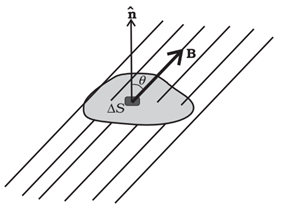
Image Source: NCERT Textbook
Consider a small vector area element ∆S of a closed surface S as in figure given above.
The number of magnetic field lines leaving the surface is balanced by the number of lines entering it. The net magnetic flux is zero.
Mathematically,
The Earth’s Magnetism
The earth behave likes a huge bar magnet. Strength of the earth’s magnetic field varies from place to place on the earth’s surface. The magnitude of the earth’s magnetic field is of the order of 10–5 T.
Causes of the Earth’s Magnetism
Exact causes the earth’s magnetism is not clear yet. There are some Earth Magnetism Theory which are as follows:
• The magnetic field of the earth is thought to arise due to electrical currents produced by convective motion of metallic fluids (consisting mostly of molten iron & nickel) in the outer core of the earth. This effect is also known as the dynamo effect.
• In outer layers of earth’s atmosphere, various gases are in ionized state. Due to rotation of the earth about its axis, strong electric current are set up due to movement of charged ions.
Basic features of the Earth’s Magnetism
Magnetic field lines of the earth resemble with a (hypothetical) giant magnetic dipole located at the centre of the earth.
The axis of the dipole does not coincide with the axis of rotation of the earth.
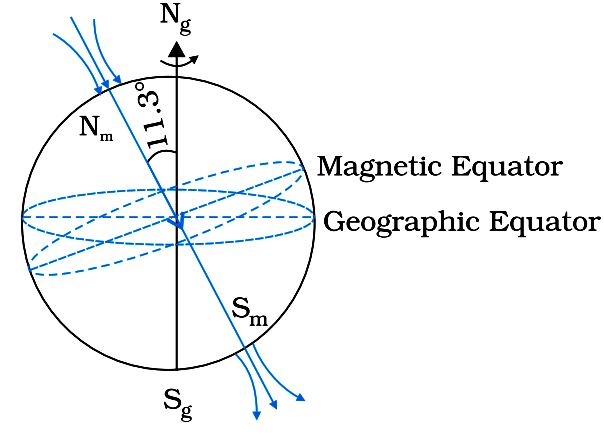
Image Source: NCERT Textbooks
• The axis of the dipole is titled by approximately 11.3º with respect to the later.
• The magnetic poles are located where the magnetic field lines due to the dipole enter or leave the earth.
• North magnetic pole is located at a latitude of 79.74º N and a longitude of 71.8º W (in north Canada)
• The magnetic south pole is located at 79.74º S, 108.22º E (in Antarctica)
• The pole near the geographic north pole of the earth is called the north magnetic pole.
• The pole near the geographic south pole of the earth is called the south magnetic pole.
• Nomenclature of the poles is confusing and one should not get confuse. If we look at the magnetic field lines of the earth (as shown in figure given above), we observe that unlike in the case of a bar magnet, the field lines go into the earth at the north magnetic pole (Nm) and come out from the south magnetic pole (Sm).
• The convention arose because the magnetic north was the direction to which the north pole of a magnetic needle pointed; the north pole of a magnet was so named as it was the north seeking pole.
• The north magnetic pole behaves like the south pole of a bar magnet inside the earth and vice versa.
Magnetic Element of the Earth’s Magnetic Field
These are the quantities which completely describe magnitude and direction of the earth’s magnetic field at a place.
There are three magnetic elements of the earth:
• Magnetic Declination
• Horizontal component of the earth’s magnetic field
• Angle of dip or Magnetic inclination
Magnetic Declination:
It is the angle between magnetic meridian and geographic meridian at a place.
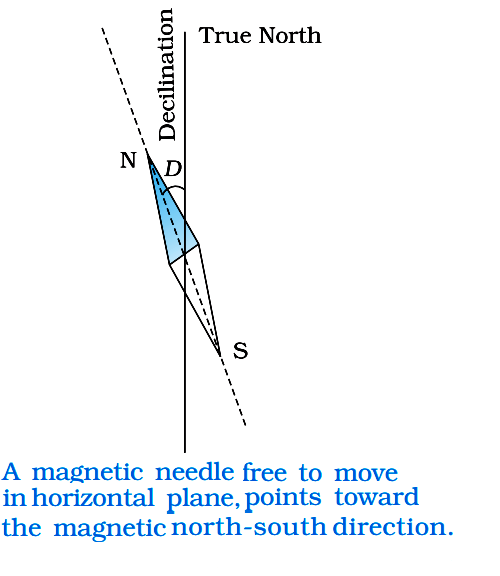
Image Source: NCERT Textbooks
In the figure shown above, the angle between the true geographic north and the north shown by a compass needle is called the magnetic declination or simply declination.
The declination is greater at higher latitudes and smaller near the equator.
Horizontal Components of the Earth’s Magnetic Field:
The earth’ magnetic field is nowhere horizontal except at equator. So, at any place, the earth’s magnetic field (BE) in the magnetic meridian may be resolved into a horizontal component (HE) and vertical component (ZE).
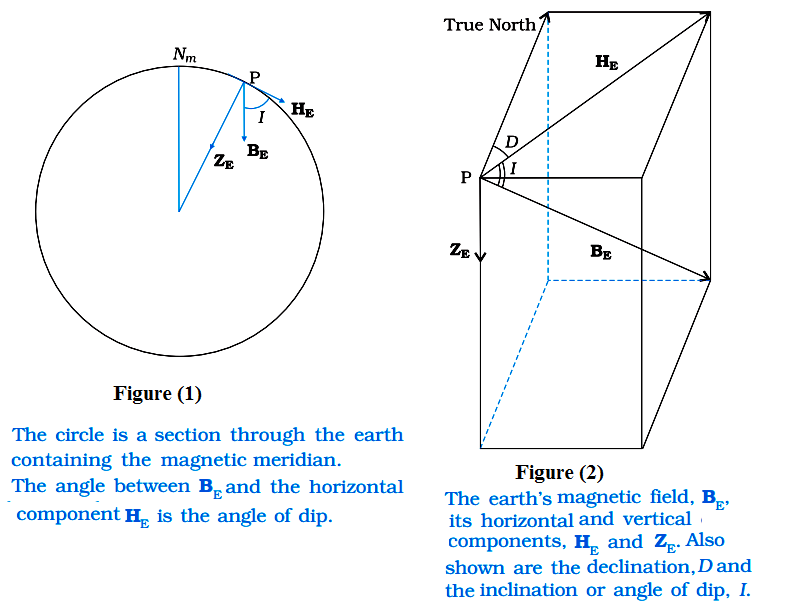
Image Source: NCERT Textbooks
The horizontal component of the earth’s magnetic field is the component of the earth’s magnetic field in horizontal direction.
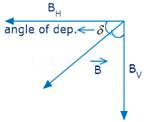
Angle of dip or Magnetic inclination
Angle of declination at a place is the angle between the direction of the earth’s magnetic field and the horizontal in the magnetic meridian at that place.
Neutral Points
At certain points the field due to a bar magnet may be completely neutralized by the horizontal component of the earth’s magnetic field. These points are known as neutral points.
Mathematical Relation between Magnetic Elements of the Earth’s Magnetic Field:
With reference to the figures given above,
ZE = BE sin I, HE = BE cos I which gives tan I = ZE/HE
Tangent Law: Superposition of magnetic fields
If a magnetic needle is under the influence of two uniform magnetic fields B1 and B2 in mutually perpendicular directions, then, the magnetic needle will align itself along the resultant field.
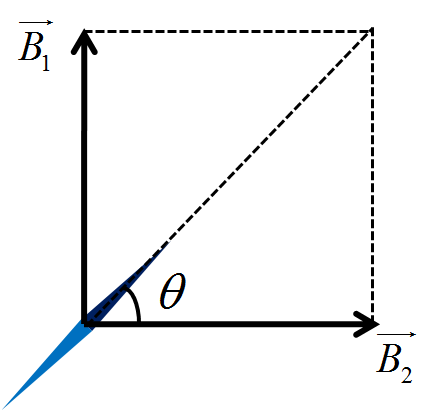
In the figure shown above, if the resultant of B1 and B2 makes an angle θ with B1, then, tan θ = |B2|/|B1|.
Atom as Magnetic Dipole
In an atom, an electron revolves around the nucleus. The orbit of electron behaves like a current loop of current which has a definite magnetic dipole moment associated with it.
Magnetic dipole moment of an orbit of radius r having electron moving with velocity ω, is given by,
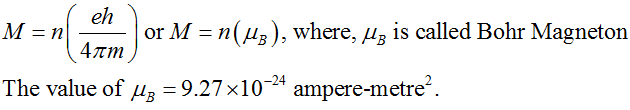
Important terms used in Magnetism
Relative Magnetic Permeability
It is the ability of a material to permit magnetic lines of force to pass through it. It is given by,
μR = (B/Bo) = (μ/μo)
Where Bo is number of magnetic lines per unit area in vacuum, B is number of magnetic lines of force per unit area in the given material medium. μ is magnetic permeability of a material and μo is magnetic permeability of free space.
μR ha no dimension and its value for vacuum is one.
Magnetic Intensity
Degree to which a magnetic field can magnetise a material is represented in terms of magnetic intensity.
It is given by, H = n i or H = B/ μ, where, n is number turns per unit length of a toroidal solenoid carrying a current i. It is a vector quantity and its SI unit is Am‒1.
Intensity of Magnetisation
Intensity of Magnetisation of a magnetic material is defined as magnetic moment per unit volume of the material.
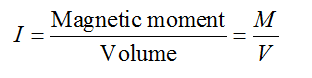
Magnetic Susceptibility
Susceptibility of a magnetic material is defined as the ratio of the intensity of magnetisation (I) induced in the material to the magnetizing force (H) applied to it.
It is given by,
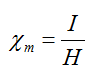
Relation between Magnetic Susceptibility and Magnetic Permeability
A magnetic material placed in a magnetising field of magnetising intensity H, the material gets magnetised. Total magnetic induction B in the material is the sum of the magnetic induction Bo in vacuum produced by the magnetic intensity and magnetic induction Bm, due to magnetisation of the material, therefore, B = Bo + Bm
Now, Bo = μo H and Bm = μo I, where I is the intensity of magnetistion induced in the magnetic material. So, B = μo (H + I)
We know that, B = μ H and I = χm H
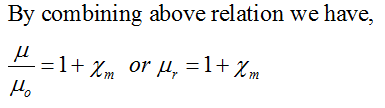
Classification of Magnetic Material
Different types of material behave differently in presence of external magnetic field and are categorised into following types:
(i) Diamagnetic Material (ii) Paramagnetic Material and (iii) Ferromagnetic Material
Diamagnetic Material
Diamagnetic substances are those which have tendency to move from stronger to the weaker part of the external magnetic field. Materials in whose atoms (molecules) or ions do not possess any net magnetic moment of their own.
Some diamagnetic materials are bismuth, copper, lead, silicon, nitrogen (at STP), water and sodium chloride.
Paramagnetic Material
Paramagnetic materials are those which get weakly magnetised when placed in an external magnetic field. They have tendency to move from a region of weak magnetic field to strong magnetic field, i.e., they get weakly attracted to a magnet.
The individual atoms (or ions or molecules) of a paramagnetic material possess a permanent magnetic dipole moment of their own.
Ferromagnetic Material
Ferromagnetic substances are those which gets strongly magnetised when placed in an external magnetic field. They have strong tendency to move from a region of weak magnetic field to strong magnetic field, i.e., they get strongly attracted to a magnet.
The individual atoms (or ions or molecules) in a ferromagnetic material possess a dipole moment as in a paramagnetic material but in a more cooperative way.
Curie’s Law in Magnetism
According to this law, the intensity of magnetization (I) of magnetic material is directly proportional to the magnetic field (H), and inversely proportional to the absolute temperature (T) of the material.
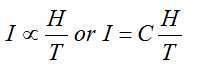
Where, C is a constant known as Curie’s constant.
Hysteresis Curve:
Hysteresis curve is the relation between magnetic induction or intensity of magnetization of a ferromagnetic material with magnetizing force or magnetic intensity.
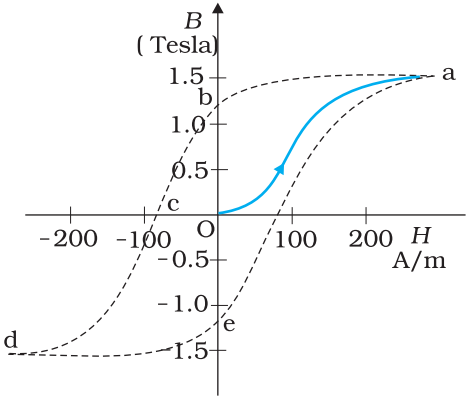
The graph given above shows hysteresis loop for ferromagnetic materials taken through one cycle of magnetisation.
CBSE Class 12 Physics Important Questions Chapter 5 – Magnetism And Matter
1 Mark Questions
1. How does the intensity of magnetization of a paramagnetic material vary with increasing applied magnetic field?
Ans. Intensity of magnetization increases with the increase in applied magnetic field.
2. An iron bar magnet is heated to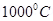 
and then cooled in a magnetic field free space. Will it retain magnetism?
Ans. Curie temperature of iron is about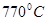 
but when it is heated to a very higher temperature magnetism of iron further gets lost and it will not retain magnetism.
3. How will the magnetic field intensity at the centre of a circular wire carrying current change, if the current through the wire is doubled and radius of the coil is halved?
Ans. Since B =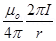 
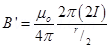
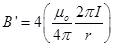
B’= 4B
4. Can neutrons be accelerated in a cyclotron? Why?
Ans. No, neutrons cannot be accelerated in a cyclotron because neutron is neutral and cyclotron can accelerate only charged particles.
5. What type of magnetic material is used in making permanent magnets?
Ans.Material having high coercivity is used in making permanent magnets.
6. Which physical quantity has the unit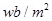 
? Is it a scalar or a vector quantity?
Ans. Magnetic field. It is a vector quantity.
2 Marks Questions
1. A bar magnet of magnetic moment M is aligned parallel to the direction of a uniform magnetic field B. What is the work done to turn the magnet, so as the align its magnetic moment?
(i) Opposite to the field direction
(ii) Normal to the field direction?
Ans. Since work done W = MB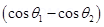 
(i) 
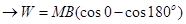
W = MB [1- (-1)]
W = 2MB
(ii)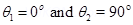 
W = MB 
W = MB
2. An electron in the ground state of hydrogen atom is revolving in anti – clock wise direction in a circular orbit. The atom is placed normal to the electron orbit makes an angle of 30o in the magnetic field. Find the torque experienced by the orbiting electron?
Ans. Magnetic moment associated with electron M =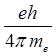 
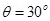
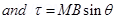
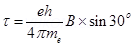
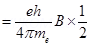
3. Define angle of dip. Deduce the relation connecting angle of dip and horizontal component of earth’s total magnetic field with the horizontal direction.
Ans.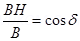 
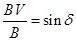
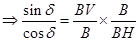
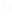
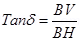
4. A point change +q is moving with speed 
perpendicular to the magnetic field B as shown in the figure. What should be the magnitude and direction of the applied electric field so that the net force acting on the charge is zero?
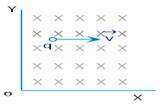
Ans. Force on the charge due to magnetic field = qVB sin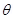
Since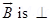 
to the plane of paper and in words
F = qVB 
F = qVB (along OY)
Force on the charge due to electric field
F = qE
Net force on change is zero if 
qE = qVB
E = VB
(along YO)
5. The energy of a charged particle moving in a uniform magnetic field does not change. Why?
Ans. The force on a charged particle in a uniform magnetic field always acts in a direction perpendicular to the motion of the charge. Since work done by the magnetic field on the charge is zero, hence energy of the charged particle will not change.
6. In the figure, straight wire AB is fixed; white the loop is free to move under the influence of the electric currents flowing in them. In which direction does the loop begin to move? Justify.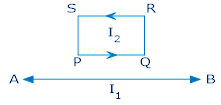
Ans. Since current in AB and arm PQ are in same direction therefore wire will attract the arm PQ with a force (say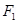
)
But repels the arm RS with a force (say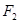
)
Sine arm PQ is closer to the wire AB
i.e. the loop will move towards the wire.
7. State two factors by which voltage sensitivity of a moving coil galvanometer can be increased?
Ans. Voltage sensitivity = 
It can be increased by
(1) increasing B using powerful magnets
(2) decreasing k by using phosphor borne strip
8. What is the magnetic moment associated with a coil of 1 turns, area of cross- section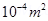 
carrying a current of 2A?
Ans. m = NIA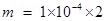
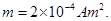
9. A Rowland ring of mean radius 15 cm has 3500 turns of wire wound on a ferromagnetic core of relative permeability 800. What is the magnetic field B in the core for a magnetising current of 1.2 A?
Ans. Mean radius of a Rowland ring, r= 15 cm = 0.15 m
Number of turns on a ferromagnetic core, N= 3500
Relative permeability of the core material, 
Magnetising current, I= 1.2 A
The magnetic field is given by the relation:
B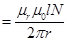 
Where,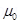
= Permeability of free space =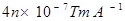 
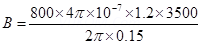
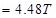
Therefore, the magnetic field is n the core is 4.48 T.
10. At a certain location in Africa, a compass points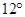 
west of the geographic north. The north tip of the magnetic needle of a dip circle placed in the plane of magnetic meridian points 
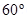above the horizontal. The horizontal component of the earth’s field is measured to be 0.16 G. Specify the direction and magnitude of the earth’s field at the location.
Ans. Angle of declination,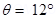 
Angle of dip, 
Horizontal component of earth’s magnetic field, BH= 0.16 G
Earth’s magnetic field at the given location = B
We can relate B and BH as: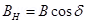
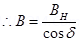
Earth’s magnetic field lies in the vertical plane, 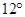West of the geographic meridian, making an angle of 60°(upward) with the horizontal direction. Its magnitude is 0.32ss G.
11. A magnetic needle free to rotate in a vertical plane parallel to the magnetic meridian has its north tip pointing down at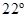 
with the horizontal. The horizontal component of the earth’s magnetic field at the place is known to be 0.35 G. Determine the magnitude of the earth’s magnetic field at the place.
Ans. Horizontal component of earth’s magnetic field, BH= 0.35 G
Angle made by the needle with the horizontal plane = Angle of dip = 
Earth’s magnetic field strength = B
We can relate B and BH as: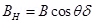
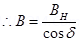
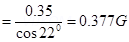
Hence, the strength of earth’s magnetic field at the given location is 0.377 G.
12. If the solenoid in Exercise 5.5 is free to turn about the vertical direction and a uniform horizontal magnetic field of 0.25 T is applied, what is the magnitude of torque on the solenoid when its axis makes an angle of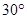 
with the direction of applied field?
Ans. Magnetic field strength, B = 0.25 T
Magnetic moment, M=
The angle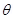, between the axis of the solenoid and the direction of the applied field is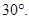 
Therefore, the torque acting on the solenoid is given as: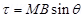
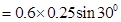
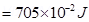
13. A closely wound solenoid of 800 turns and area of cross section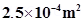 
carries a current of 3.0 A. Explain the sense in which the solenoid acts like a bar magnet. What is its associated magnetic moment?
Ans. Number of turns in the solenoid, n = 800
Area of cross-section, A= 
Current in the solenoid, I= 3.0 A
A current-carrying solenoid behaves as a bar magnet because a magnetic field develops along its axis, i.e., along its length.
The magnetic moment associated with the given current-carrying solenoid is calculated as:
M= n I A
= 
= 
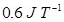
14. A short bar magnet placed with its axis at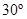 
with a uniform external magnetic field of 0.25 T experiences a torque of magnitude equal to 
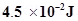. What is the magnitude of magnetic moment of the magnet?
Ans. Magnetic field strength, B= 0.25 T
Torque on the bar magnet, T=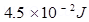
Angle between the bar magnet and the external magnetic field,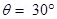 
Torque is related to magnetic moment (M) as:
T= MB sin θ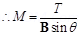
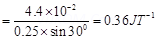
Hence, the magnetic moment of the magnet is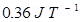
.
3 Marks Questions
1. A short bar magnet of magnetic moment 0.9 J/T is placed with its axis at 60o to a uniform magnetic field. It experiences a torque of 0.063 Nm. (i) calculate the strength of the magnetic field and (ii) what orientation of the bar magnet corresponds to the equilibrium position in the magnetic field?
Ans. (i) Since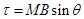 
Here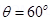 
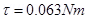
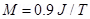
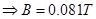
(ii) The magnet will be in stable equilibrium in the magnetic field if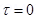 
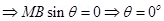
i.e When magnet aligns itself parallel to the field
2. A beam of electrons is moving with a velocity of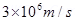 
and carries a current of 1 
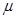A.
(a) How many electrons per second pass a given point?
(b) How many electrons are in 1m of the beam?
(c) What is the total force on all the electrons in 1m of the beam if it passes through the field of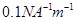 
?
Ans.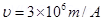 
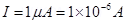
(a)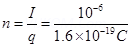 
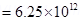
(b) Electrons traverse a distance of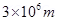 
in 1 s
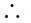No. of electrons in 1 meter of the beam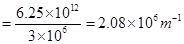
(c) Force on 1 meter of the beam of electrons
3. What is the main function of soft iron core used in a moving coil galvanometer? A galvanometer gives full deflection for Ig. Can it be converted into an ammeter of range I < Ig?
Ans. Soft iron core is used the moving coil galvanometer because it increases the strength of the magnetic field thus increases the sensitivity of the galvanometer.
We know S =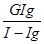 
For I < Ig, S becomes negative
Hence it cannot be converted into an ammeter of range I < Ig.
4. Two wires loops PQRSP formed by joining two semicircular wires of radii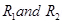 
carries a current I as shown in the figure. What is the direction of the magnetic induction at the centre C.?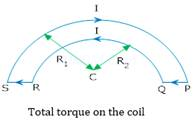
Ans. Magnetic field due to semicircle QR at C. is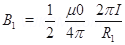
Magnetic field due to semicircle is at C is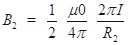
Net field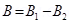 
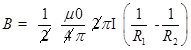
5. A circular coil is placed in uniform magnetic field of strength 0.10T normal to the plane of coil. If current in the coil is 5.0A. Find.
(a) Total torque on the coil
(b) Total force on the coil
(c) Average force on each electron due to magnetic field
(The coil is made of copper wire of cross- sectional area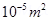 
and free electron density in copper is 
)
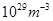Ans. (a) B = 0.10T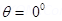
(Normal to plane of the coil)
I = 5.0 A, Area = 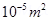n =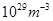 
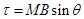
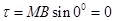
(b) Total force on the coil = 0 Newton
(c) Fav = q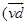 
)
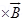(I = neAVd)
Fav =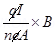 
Fav =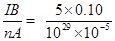 
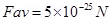
6. Using Ampere’s circuital law, derive an expression for magnetic field along the axis of a Toroidal solenoid?
Ans. If n be the no, of turns per unit length I be the current flowing through the Toroid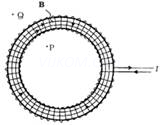
Then from Ampere’s circuital law
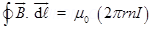
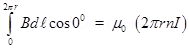
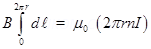
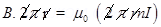
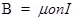
7. A short bar magnet of magnetic moment m =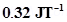 
is placed in a uniform magnetic field of 0.15 T. If the bar is free to rotate in the plane of the field, which orientation would correspond to its (a) stable, and (b) unstable equilibrium? What is the potential energy of the magnet in each case?
Ans. Moment of the bar magnet, M= 
External magnetic field, B= 0.15 T
(a) The bar magnet is aligned along the magnetic field. This system is considered as being in stable equilibrium. Hence, the angle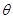
, between the bar magnet and the magnetic field is
.
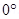Potential energy of the system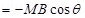
(b) The bar magnet is oriented 180°to the magnetic field. Hence, it is in unstable equilibrium.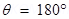
Potential energy = – MB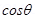 
8. A closely wound solenoid of 2000 turns and area of cross-section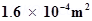 
, carrying a current of 4.0 A, is suspended through its centre allowing it to turn in a horizontal plane.
(a) What is the magnetic moment associated with the solenoid?
(b) What is the force and torque on the solenoid if a uniform horizontal magnetic field of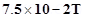 
is set up at an angle of 
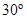with the axis of the solenoid?
Ans. Number of turns on the solenoid, n = 2000
Area of cross-section of the solenoid, A= 
Current in the solenoid, I= 4 A
(a) The magnetic moment along the axis of the solenoid is calculated as:
M= nAI
= 
= 1.28 A
(b) Magnetic field, B =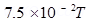
Angle between the magnetic field and the axis of the solenoid,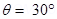 
Torque,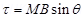 
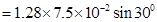
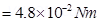
Since the magnetic field is uniform, the force on the solenoid is zero. The torque on the solenoid i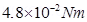s 
s
9. A circular coil of 16 turns and radius 10 cm carrying a current of 0.75 A rests with its plane normal to an external field of magnitude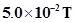 
. The coil is free to turn about an axis in its plane perpendicular to the field direction. When the coil is turned slightly and released, it oscillates about its stable equilibrium with a frequency of 
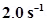. What is the moment of inertia of the coil about its axis of rotation?
Ans.Number of turns in the circular coil, N= 16
Radius of the coil, r= 10 cm = 0.1 m
Cross-section of the coil, A=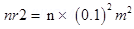
Current in the coil, I= 0.75 A
Magnetic field strength, B=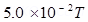
Frequency of oscillations of the coil, v=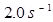
∴Magnetic moment, M= NIA 
= 
= 
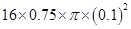
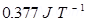
Frequency is given by the relation: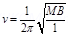
Where,
I= Moment of inertia of the coil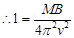
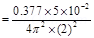
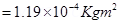
Hence, the moment of inertia of the coil about its axis of rotation is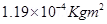 
10. A short bar magnet has a magnetic moment of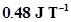 
. Give the direction and magnitude of the magnetic field produced by the magnet at a distance of 10 cm from the centre of the magnet on (a) the axis, (b) the equatorial lines (normal bisector) of the magnet.
Ans. Magnetic moment of the bar magnet, M=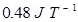 
(a) Distance, d = 10 cm = 0.1 m
The magnetic field at distance d, from the centre of the magnet on the axis is given by the relation: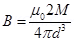
ss
Where,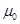
= Permeability of free space =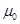 
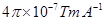
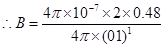
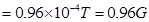
The magnetic field is along the S – N direction.
(b) The magnetic field at a distance of 10 cm (i.e., d= 0.1 m) on the equatorial line of the magnet is given as: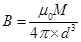
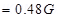
The magnetic field is along the N – S direction.
11. A short bar magnet placed in a horizontal plane has its axis aligned along the magnetic north-south direction. Null points are found on the axis of the magnet at 14 cm from the centre of the magnet. The earth’s magnetic field at the place is 0.36 G and the angle of dip is zero. What is the total magnetic field on the normal bisector of the magnet at the same distance as the null-point (i.e., 14 cm) from the centre of the magnet? (At null points, field due to a magnet is equal and opposite to the horizontal component of earth’s magnetic field.)
Ans. Earth’s magnetic field at the given place, H= 0.36 G
The magnetic field at a distance d, on the axis of the magnet is given as:
……(i)
Where,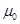= Permeability of free space
M= Magnetic moment
The magnetic field at the same distance d, on the equatorial line of the magnet is given as: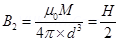
[Using equation (i)]
Total magnetic field,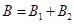
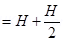
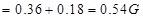
Hence, the magnetic field is 0.54 G in the direction of earth’s magnetic field.
12. A long straight horizontal cable carries a current of 2.5 A in the direction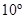 
south of west to 10°north of east. The magnetic meridian of the place happens to be 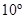west of the geographic meridian. The earth’s magnetic field at the location is 0.33 G, and the angle of dip is zero. Locate the line of neutral points (ignore the thickness of the cable). (At neutral points, magnetic field due to a current-carrying cable is equal and opposite to the horizontal component of earth’s magnetic field.)
Ans. Current in the wire, I= 2.5 A
Angle of dip at the given location on earth,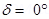 
Earth’s magnetic field, H= 0.33 G =
The horizontal component of earth’s magnetic field is given as: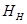
= H cos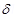 
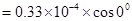
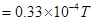
The magnetic field at the neutral point at a distance Rfrom the cable is given by the relation: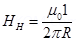
Where,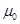 = Permeability of free space =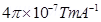 
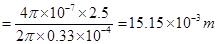
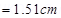
Hence, a set of neutral points parallel to and above the cable are located at a normal distance of 1.51 cm.
13. A compass needle free to turn in a horizontal plane is placed at the centre of circular coil of 30 turns and radius 12 cm. The coil is in a vertical plane making an angle of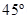 
with the magnetic meridian. When the current in the coil is 0.35 A, the needle points west to east.
(a) Determine the horizontal component of the earth’s magnetic field at the location.
(b) The current in the coil is reversed, and the coil is rotated about its vertical axis by an angle of 90º in the anticlockwise sense looking from above. Predict the direction of the needle. Take the magnetic declination at the places to be zero.
Ans. Number of turns in the circular coil, N= 30
Radius of the circular coil, r= 12 cm = 0.12 m
Current in the coil, I= 0.35 A
Angle of dip,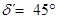 
(a) The magnetic field due to current I, at a distance r, is given a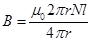s:
s
Where,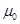 = Permeability of free space =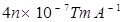 
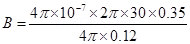s
= 
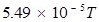
The compass needle points from West to East. Hence, the horizontal component of earth’s magnetic field is given as: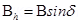
=
(b) When the current in the coil is reversed and the coil is rotated about its vertical axis by an angle of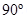
, the needle will reverse its original direction. In this case, the needle will point from East to West.
14. A magnetic dipole is under the influence of two magnetic fields. The angle between the field directions is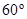 
, and one of the fields has a magnitude of 
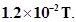If the dipole comes to stable equilibrium at an angle of 
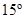with this field, what is the magnitude of the other field?
Ans. Magnitude of one of the magnetic fields
Magnitude of the other magnetic field =
Angle between the two fields,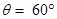 
At stable equilibrium, the angle between the dipole and field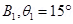 
Angle between the dipole and field 
= 
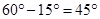
At rotational equilibrium, the torques between both the fields must balance each other.
∴ Torque due to field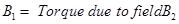 
Where,
M= Magnetic moment of the dipole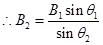
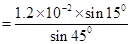
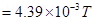s
Hence, the magnitude of the other magnetic field is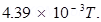 
15. The magnetic moment vectors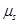 
and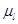 
associated with the intrinsic spin angular momentum S and orbital angular momentum l, respectively, of an electron are predicted by quantum theory (and verified experimentally to a high accuracy) to be given by:
, 
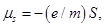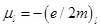Which of these relations is in accordance with the result expected classically? Outline the derivation of the classical result.
Ans. The magnetic moment associated with the orbital angular momentum is valid with the classical mechanics.
The magnetic moment associated with the orbital angular (l) momentum is given as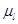
For current i and area of cross-section A, we have the relation:
Magnetic moment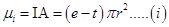
Where,
e = Charge of the electron
r = Radius of the circular orbit
T = Time taken to complete one rotation around the circular orbit of radius r
Angular momentum,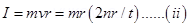
Where,
M = Mass of the electron
V = Velocity of the electorn
Dividing equation (1) by equation (2),we get:
Therefore of the two relations,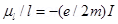
is in accordance with class physics.
5 Marks Questions
1. A particle of mass m and charge q moving with a uniform speed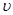 
normal to a uniform magnetic field B describes a circular path of radius & Derive expressions for (1) Radius of the circular path (2) time period of revolution (3) Kinetic energy of the particle?
Ans. A particle of mass (m) and change (q) moving with velocity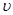 normal to 
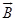describes a circular path if
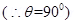
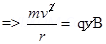
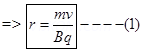
Since Time period of Revolution
During circular path = 
=> 
(
)
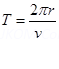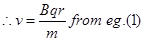=> T = 
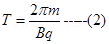
Kinetic energy K.E =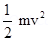 
=> KE =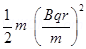 
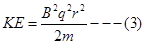
2. Write an expression for the force experienced by the charged particle moving in a uniform magnetic field B With the help of labeled diagram explain the working of cyclotron? Show that cyclotron frequency does not depend upon the speed of the particle?
Ans. Force experienced by the charged particle moving at right angles to uniform magnetic field 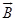with velocity 
is given by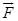 
= q (
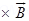) Initially Dee 
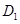is negatively charged and Dee 
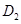is positively charged so, the positive ion will get accelerated towards Dee 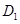since the magnetic field is uniform and acting at right angles to the plane of the Dees so the ion completes a circular path in 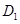when ions comes out into the gap, polarity of the Dee’s gets reversed used the ion is further accelerated towards Dee with greater speed and cover a bigger semicircular path. This process is separated time and again and the speed of the ion becomes faster till it reaches the periphery of the dees where it is brought out by means of a deflecting plate and is made to bombard the target.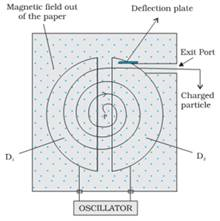
Since F = qVBsin900 provides the necessary centripetal force to the ion to cover a circular path so we can say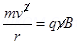 
=> r = 
Time period =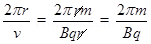 
V =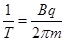 
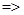frequency is independent of velocity
3. (a) Obtain an expression for the torque acting on a current carrying circular loop.
(b) What is the maximum torque on a galvanometer coil 5 cm 
12 cm of 600 turns when carrying a current of 10-5 A. in a field where flux density is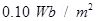 
?
Ans. ABCD is a rectangular loop of length (L), breadth (b) and area (A). Let I be the Current flowing in the anti clockwise direction. Let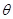 
be the angle between the normal to the loop and magnetic field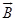 
Force acting on arm AB of the loop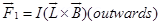
Force on arm CD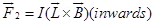
Force on arm BC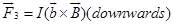
Force on arm DA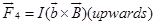
Since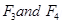 
are equal and opposite and also acts along the same line, hence they cancel each other.
are also equal and opposite but their line of action is different, so they form a couple and makes the rectangular loop rotate anti clockwise.
Thus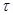 
= either force 
distance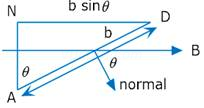
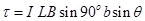
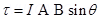
For loop of N turns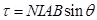
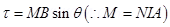
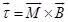
Where M is magnetic moment of the loop.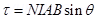
Torque will be maximum when 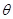= 90o
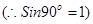
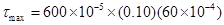
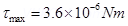
4. The current sensitivity of a moving coil galvanometer increases by 20% when its resistance is increased by a factor of two. Calculate by what factor, the voltage sensitivity changes?
Ans. Current sensitivity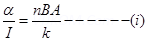 
Voltage sensitivity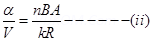 
Resistance of a galvanometer increases when n and A are changed
Given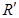 
= 2R
Then n =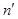 
and A =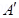 
New current sensitivity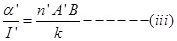
New voltage sensitivity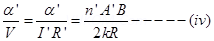
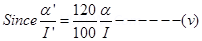
From (i) and (iii)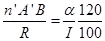
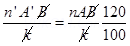
n’A’=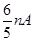
Using equation (iv)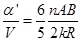
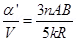
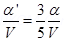
Thus voltage sensitivity decreases by a factor of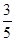 
.
5. (a) Show how a moving coil galvanometer can be converted into an ammeter?
(b) A galvanometer has a resistance 30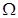 
and gives a full scale deflection for a current of 2mA. How much resistance in what way must be connected to convert into?
(1) An ammeter of range 0.3A
(2) A voltammeter of range 0.2V.
Ans. (a) A galvanometer can be converted into an ammeter by connecting a low resistance called shunt parallel to the galvanometer.
Since G and RS are in parallel voltage across then is same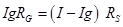 
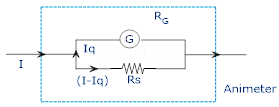
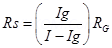
(b) (1) I = 0.3A G = 30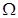 Ig = 2mA =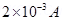 
Sheent (S) =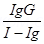 
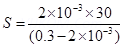
S = 0.2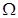
(2) G = 30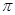
, Ig = 2mA =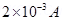, V = 0.2V
Shunt Resistance (R)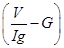 
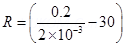
R = 70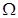
6. A monoenergetic (18 keV) electron beam initially in the horizontal direction is subjected to a horizontal magnetic field of 0.04 G normal to the initial direction. Estimate the up or down deflection of the beam over a distance of 30 cm (me=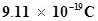 
). [Note: Data in this exercise are so chosen that the answer will give you an idea of the effect of earth’s magnetic field on the motion of the electron beam from the electron gun to the screen in a TV set.]
Ans. Energy of an electron beam, E= 18 keV =
Charge on an electron, e=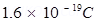 
E=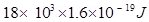
Magnetic field, B = 0.04 G
Mass of an electron, me= 
Distance up to which the electron beam travels, d = 30 cm = 0.3 m
We can write the kinetic energy of the electron beam as: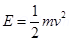
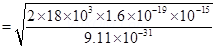
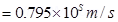
The electron beam deflects along a circular path of radius, r.
The force due to the magnetic field balances the centripetal force of the path.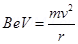
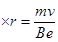
” data-src=”https://iitianacademy.com/wp-content/uploads/2021/03/img_60596b18c2483.png” />
Let the up and down deflection of the electron beam be ” data-src=”https://iitianacademy.com/wp-content/uploads/2021/03/img_60596b1952c8c.png” />
Where,
θ= Angle of declination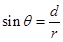
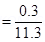
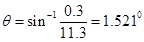
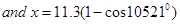
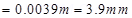
Therefore, the up and down deflection of the beam is 3.9 mm.
7. A sample of paramagnetic salt contains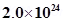 
atomic dipoles each of dipole moment 
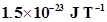. The sample is placed under a homogeneous magnetic field of 0.64 T, and cooled to a temperature of 4.2 K. The degree of magnetic saturation achieved is equal to 15%. What is the total dipole moment of the sample for a magnetic field of 0.98 T and a temperature of 2.8 K? (Assume Curie’s law)
Ans. Number of atomic dipoles, n=
Dipole moment of each atomic dipole, M= 
When the magnetic field,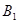 
= 0.64 T
The sample is cooled to a temperature,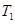 
= 4.2°K
Total dipole moment of the atomic dipole, 
= 
= 
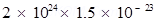
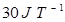
Magnetic saturation is achieved at 15%.
Hence, effective dipole moment,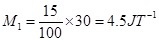 
When the magnetic field,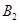 
= 0.98 T
Temperature,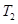 
= 2.8°K
Its total dipole moment =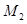
According to Curie’s law, we have the ratio of two magnetic dipoles as: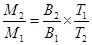
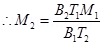
Therefore,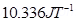 
is the total dipole moment of the sample for a magnetic field of 0.98 T and a temperature of 2.8 K.
8. A telephone cable at a place has four long straight horizontal wires carrying a current of 1.0 A in the same direction east to west. The earth’s magnetic field at the place is 0.39 G, and the angle of dip is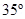 
. The magnetic declination is nearly zero. What are the resultant magnetic fields at points 4.0 cm below the cable?
Ans. Number of horizontal wires in the telephone cable, n= 4
Current in each wire,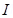 
= 1.0 A
Earth’s magnetic field at a location, H= 0.39 G =
Angle of dip at the location,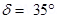 
Angle of declination,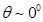 
For a point 4 cm below the cable:
Distance, r = 4 cm = 0.04 m
The horizontal component of earth’s magnetic field can be written as:
Where,
B= Magnetic field at 4 cm due to current I in the four wires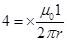
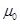= Permeability of free space =
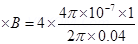
= 0
= 0.2 G
∴ 
= 
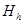
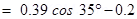
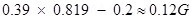
The vertical component of earth’s magnetic field is given as:
Hv= Hsin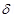
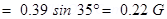
The angle made by the field with its horizontal component is given as: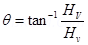
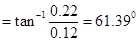
The resultant field at the point is given a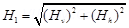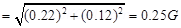s:
s
For a point 4 cm above the cable:
Horizontal component of earth’s magnetic field: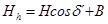
= 0.39 cos 35° + 0.2 = 0.52 G
Vertical component of earth’s magnetic field:
= 0.39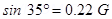
Angle, 
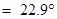
And resultant field: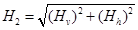
9. Answer the following questions:
(a) Explain qualitatively on the basis of domain picture the irreversibility in the magnetisation curve of a ferromagnet.
(b) The hysteresis loop of a soft iron piece has a much smaller area than that of a carbon steel piece. If the material is to go through repeated cycles of magnetisation, which piece will dissipate greater heat energy?
(c) ‘A system displaying a hysteresis loop such as a ferromagnet, is a device for storing memory?’ Explain the meaning of this statement.
(d) What kind of ferromagnetic material is used for coating magnetic tapes in a cassette player, or for building ‘memory stores’ in a modern computer?
(e) A certain region of space is to be shielded from magnetic fields.
Suggest a method.
Ans. The hysteresis curve (B–H curve) of a ferromagnetic material is shown in the following figure.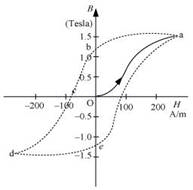
(a) It can be observed from the given curve that magnetisation persists even when the external field is removed. This reflects the irreversibility of a ferromagnet.
(b) The dissipated heat energy is directly proportional to the area of a hysteresis loop. A carbon steel piece has a greater hysteresis curve area. Hence, it dissipates greater heat energy.
(c) The value of magnetisation is memory or record of hysteresis loop cycles of magnetisation. These bits of information correspond to the cycle of magnetisation. Hysteresis loops can be used for storing information.
(d) Ceramic is used for coating magnetic tapes in cassette players and for building memory stores in modern computers.
(e) A certain region of space can be shielded from magnetic fields if it is surrounded by soft iron rings. In such arrangements, the magnetic lines are drawn out of the region.
10. Answer the following questions:
(a) Why does a paramagnetic sample display greater magnetisation (for the same magnetising field) when cooled?
(b) Why is diamagnetism, in contrast, almost independent of temperature?
(c) If a to roid uses bismuth for its core, will the field in the core be (slightly) greater or (slightly) less than when the core is empty?
(d) Is the permeability of a ferromagnetic material independent of the magnetic field? If not, is it more for lower or higher fields?
(e) Magnetic field lines are always nearly normal to the surface of a ferromagnetic at every point. (This fact is analogous to the static electric field lines being normal to the surface of a conductor at every point.) Why?
(f) Would the maximum possible magnetisation of a paramagnetic sample be of the same order of magnitude as the magnetization of a ferromagnet?
Ans. (a)Owing to therandom thermal motion of molecules, the alignments of dipoles get disrupted at high temperatures. On cooling, this disruption is reduced. Hence, a paramagnetic sample displays greater magnetisation when cooled.
(b) The induced dipole moment in a diamagnetic substance is always opposite to the magnetising field. Hence, the internal motion of the atoms (which is related to the temperature) does not affect the diamagnetism of a material.
(c) Bismuth is a diamagnetic substance. Hence, a toroid with a bismuth core has a magnetic field slightly greater than a toroid whose core is empty.
(d) The permeability of ferromagnetic materials is not independent of the applied magnetic field. It is greater for a lower field and vice versa.
(e) The permeability of a ferromagnetic material is not less than one. It is always greater than one. Hence, magnetic field lines are always nearly normal to the surface of such materials at every point.
(f) The maximum possible magnetisation of a paramagnetic sample can be of the same order of magnitude as the magnetisation of a ferromagnet. This requires high magnetising fields for saturation.
11. A short bar magnet of magnetic moment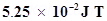 
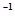is placed with its axis perpendicular to the earth’s field direction. At what distance from the centre of the magnet, the resultant field is inclined at 45º with earth’s field on s
(a) its normal bisector and (b) its axis. Magnitude of the earth’s field at the place is given to be 0.42 G. Ignore the length of the magnet in comparison to the distances involved.
Ans. Magnetic moment of the bar magnet, M=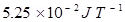 
Magnitude of earth’s magnetic field at a place, H= 0.42 G =
(a) The magnetic field at a distance R from the centre of the magnet on the normal bisector is given by the relation:
Where,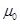 = Permeability of free space =
When the resultant field is inclined at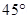 
with earth’s field, B= H
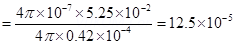
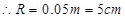
(b) The magnetic field at a distanced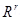
from the centre of the magnet on its axis is given as: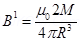
The resultant field is inclined at 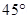with earth’s field.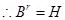
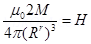
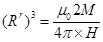
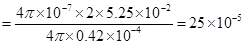
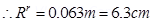
12. If the bar magnet in exercise 5.13 is turned around by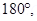 
where will the new null points be located?
Ans. The magnetic field on the axis of the magnet at a distance d1= 14 cm, can be written as:
…(i)
Where,
M = Magnetic moment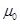= Permeability of free space
H= Horizontal component of the magnetic field at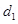 
If the bar magnet is turned through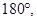 
then the neutral point will lie on the equatorial line.
Hence, the magnetic field at a distance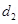 
, on the equatorial line of the magnet can be written as:
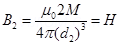……(2)
Equating equations (1) and (2), we get: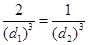
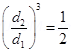s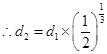
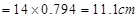
The new null points will be located 11.1 cm on the normal bisector.
13. A bar magnet of magnetic moment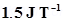 
lies aligned with the direction of a uniform magnetic field of 0.22 T.
(a) What is the amount of work required by an external torque to turn the magnet so as to align its magnetic moment: (i) normal to the field direction, (ii) opposite to the field direction?
(b) What is the torque on the magnet in cases (i) and (ii)?
Ans. (a) Magnetic moment, M=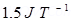 
Magnetic field strength, B= 0.22 T
(i) Initial angle between the axis and the magnetic field, 
= 0° Final angle between the axis and the magnetic field, 
The work required to make the magnetic moment normal to the direction of magnetic field is given as: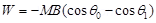
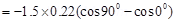
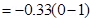
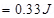
(ii) Initial angle between the axis and the magnetic field,
Final angle between the axis and the magnetic field, 
The work required to make the magnetic moment opposite to the direction of magnetic field is given as: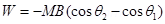
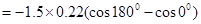
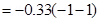
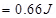
(b) For case (i):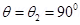 
∴Torque,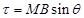 
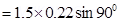
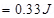
For case (ii):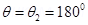 
∴ Torque, 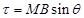ss
14. Answer the following questions regarding earth’s magnetism:
(a) A vector needs three quantities for its specification. Name the three independent quantities conventionally used to specify the earth’s magnetic field.
(b) The angle of dip at a location in southern India is about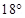 
.
Would you expect a greater or smaller dip angle in Britain?
(c) If you made a map of magnetic field lines at Melbourne in Australia, would the lines seem to go into the ground or come out of the ground?
(d) In which direction would a compass free to move in the vertical plane point to, if located right on the geomagnetic north or south pole?
(e) The earth’s field, it is claimed, roughly approximates the field due to a dipole of magnetic moment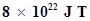 
located at its centre. Check the order of magnitude of this number in some way.
(f) Geologists claim that besides the main magnetic N-S poles, there are several local poles on the earth’s surface oriented in different directions. How is such a thing possible at all?
Ans. (a) The three independent quantities conventionally used for specifying earth’s magnetic field are:
(i) Magnetic declination,
(ii) Angle of dip, and
(iii) Horizontal component of earth’s magnetic field
(b) The angle of dip at a point depends on how far the point is located with respect to the North Pole or the South Pole. The angle of dip would be greater in Britain (it is about 70°) than in southern India because the location of Britain on the globe is closer to the magnetic North Pole.
(c) It is hypothetically considered that a huge bar magnet is dipped inside earth with its north pole near the geographic South Pole and its south pole near the geographic North Pole.
Magnetic field lines emanate from a magnetic north pole and terminate at a magnetic south pole. Hence, in a map depicting earth’s magnetic field lines, the field lines at Melbourne, Australia would seem to come out of the ground.
(d) If a compass is located on the geomagnetic North Pole or South Pole, then the compass will be free to move in the horizontal plane while earth’s field is exactly vertical to the magnetic poles. In such a case, the compass can point in any direction.
(e) Magnetic moment, M=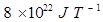
Radius of earth, r=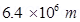 
Magnetic field strength,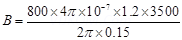
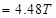
Where,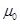 = Permeability of free space =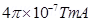 
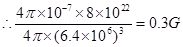
This quantity is of the order of magnitude of the observed field on earth.
(f) Yes, there are several local poles on earth’s surface oriented in different directions. A magnetised mineral deposit is an example of a local N-S pole.
15. Answer the following questions:
(a) The earth’s magnetic field varies from point to point in space.
Does it also change with time? If so, on what time scale does it change appreciably?
(b) The earth’s core is known to contain iron. Yet geologists do not regard this as a source of the earth’s magnetism. Why?
(c) The charged currents in the outer conducting regions of the earth’s core are thought to be responsible for earth’s magnetism. What might be the ‘battery’ (i.e., the source of energy) to sustain these currents?
(d) The earth may have even reversed the direction of its field several times during its history of 4 to 5 billion years. How can geologists know about the earth’s field in such distant past?
(e) The earth’s field departs from its dipole shape substantially at large distances (greater than about 30,000 km). What agencies may be responsible for this distortion?
(f) Interstellar space has an extremely weak magnetic field of the order of 10-12 T. Can such a weak field be of any significant consequence? Explain.
[Note: Exercise 5.2 is meant mainly to arouse your curiosity. Answers to some questions above are tentative or unknown. Brief answers wherever possible are given at the end. For details, you should consult a good text on geomagnetism.]
Ans. (a) Earth’s magnetic field changes with time. It takes a few hundred years to change by an appreciable amount. The variation in earth’s magnetic field with the time cannot be neglected.
(b) Earth’s core contains molten iron. This form of iron is not ferromagnetic. Hence, this is not considered as a source of earth’s magnetism.
(c) The radioactivity in earth’s interior is the source of energy that sustains the currents in the outer conducting regions of earth’s core. These charged currents are considered to be responsible for earth’s magnetism.
(d) Earth reversed the direction of its field several times during its history of 4 to 5 billion years. These magnetic fields got weakly recorded in rocks during their solidification. One can get clues about the geomagnetic history from the analysis of this rock magnetism.
(e) Earth’s field departs from its dipole shape substantially at large distances (greater than about 30,000 km) because of the presence of the ionosphere. In this region, earth’s field gets modified because of the field of single ions. While in motion, these ions produce the magnetic field associated with them.
(f) An extremely weak magnetic field can bend charged particles moving in a circle. This may not be noticeable for a large radius path. With reference to the gigantic interstellar space, the deflection can affect the passage of charged particles.