SAT MAth Practice questions – all topics
- Algebra Weightage: 35% Questions: 13-15
- Linear equations in one variable
- Linear equations in two variables
- Linear functions
- Systems of two linear equations in two variables
- Linear inequalities in one or two variables
SAT MAth and English – full syllabus practice tests
[Calc] Question Easy
The line graph shows the number of near-Earth asteroids discovered by the Spacewatch survey from 2003 to 2010.

During which period was the increase in the number of near-Earth asteroids discovered the greatest?
A) From 2003 to 2004
B) From 2004 to 2005
C) From 2005 to 2006
D) From 2007 to 2008
▶️Answer/Explanation
Ans:D
We will compare the increase in the number of near-Earth asteroids discovered from year to year by examining the vertical distances between points on the graph.
1. From 2003 to 2004:
In 2003, the number of asteroids discovered is approximately 50.8.
In 2004, the number of asteroids discovered is approximately 70.2.
Increase: \( 70.2 – 50.8 = 19.4 \).
2. From 2004 to 2005:
In 2004, the number of asteroids discovered is approximately 70.2.
In 2005, the number of asteroids discovered is approximately 80.3.
Increase: \( 80.3 – 70.2 = 10.1 \).
3. From 2005 to 2006:
In 2005, the number of asteroids discovered is approximately 80.3.
In 2006, the number of asteroids discovered is approximately 90.9.
Increase: \( 90.9 – 80.3 = 10.6 \).
4. From 2007 to 2008:
In 2007, the number of asteroids discovered is approximately 40.8.
In 2008, the number of asteroids discovered is approximately 80.4.
Increase: \( 80.4 – 40.8 = 39.6 \).
By comparing these increases, we see that the greatest increase occurred from 2007 to 2008.
[ calc] Question Easy
The linear function \(f\) is defined by \(f(x)=2(x-1)\). What is the value of \(f(4)\) ?
A) 1.5
B) 3
C) 6
D) 7
▶️Answer/Explanation
Ans: C
The linear function \( f \) is defined by:
\[ f(x) = 2(x-1) \]
We need to find the value of \( f(4) \).
1. Substitute \( x = 4 \) into the function:
\[ f(4) = 2(4-1) \]
2. Simplify inside the parentheses:
\[ f(4) = 2(3) \]
3. Multiply:
\[ f(4) = 6 \]
So, the correct answer is:
\[ \boxed{C} \]
[Calc] Question Easy

The graph of a linear equation and the graph of a quadratic equation are shown. What is true about the point \((-1,4)\) ?
A) The point satisfies only the quadratic equation
B) The point satisfies only the linear equation.
C) The point satisfies both equations.
D) The point satisfies neither equation.
▶️Answer/Explanation
Ans:C
For the linear equation represented by the straight line: Let’s call this equation y = mx + b, where m is the slope and b is the y-intercept. The point (-1, 4) is on this line, so if I substitute x = -1 and y = 4, it should satisfy the equation. 4 = m(-1) + b Solving for b using the point’s coordinates gives b = 4 + m
For the quadratic equation represented by the parabola: Let’s call this y = ax^2 + bx + c, where a, b, c are constants. Substituting x = -1 and y = 4, we get:
$4 = a(-1)^2 + b(-1) + c$ $
4 = a + (-b) + c$
Therefore, the point (-1, 4) satisfies both the linear and quadratic equations shown.
[Calc] Question Easy
Jaqueline spent \(\$ 150\) for supplies and gas to start a lawn-mowing service. She charges \$25 for each lawn she mows. In the first week Jaqueline made \(\$ 50\) after the cost of supplies and gas was deducted. Which equation represents this situation, where \(x\) is the number of lawns Jaqueline mowed during the first week?
A) \(25 x-150=50\)
B) \(50-25 x=150\)
C) \(150-25 x=50\)
D) \(25 x+50=150\)
▶️Answer/Explanation
Ans: A
Jaqueline’s earnings can be represented by the equation \(25x – 150 = 50\), where \(x\) is the number of lawns she mowed during the first week. She earns \(\$ 25\) for each lawn mowed, and after deducting the initial cost of \(\$ 150\), she made a profit of \(\$ 50\).
So, the correct equation is:
\[25x – 150 = 50\]
[Calc] Question Easy
y= 4 − 𝑥
What is the graph of the given equation?
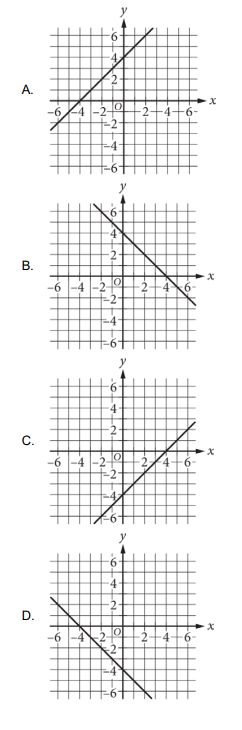
▶️Answer/Explanation
Ans: B
Analyzing the Equation:
1. Slope \((m)\) :
The equation \(y=4-x\) can be rewritten as \(y=-x+4\). Thus, the slope \(m\) is -1 .
2. Y-intercept \((b)\) :
The \(y\)-intercept \(b\) is 4 .
From this graph has negative slope and positive intercept which is only in option – B
[Calc] Question Easy
The function \(f\) is defined by \(f(x)=17 x+13\). What is the value of \(f(8)\) ?
A) 38
B) 121
C) 136
D) 149
▶️Answer/Explanation
D
Given the function \(f(x) = 17x + 13\), we need to find \(f(8)\).
Substitute \(x = 8\) into the function:
\[ f(8) = 17(8) + 13 \]
\[ f(8) = 136 + 13 \]
\[ f(8) = 149 \]
So the answer is:
\[ \boxed{D) \, 149} \]
[Calc] Question Easy

The line models the relationship between body weight and foot length for a group of infants. Based on the model, what is the predicted weight, in kilograms (kg), of an infant with a foot length of 9 centimeters \((\mathrm{cm})\) ?
A) 5
B) 7
C) 9
D) 11
▶️Answer/Explanation
B
When x= 9 the value of y is 7 from graph

[Calc] Question Easy
The function f is defined by 𝑓(𝑥) = 𝑥 + 4. What is the value of 𝑓(𝑥) when 𝑥 = 5?
A. 9
B. 5
C. 4
D. 1
▶️Answer/Explanation
Ans: A
The function \( f(x) = x + 4 \) defines the value of \( f(x) \). We need to find the value when \( x = 5 \).
Substitute \( x = 5 \) into the function:
\[
f(5) = 5 + 4 = 9
\]
So, the value of \( f(x) \) when \( x = 5 \) is \( 9 \).
[Calc] Question Easy

What is an equation of the graph shown?
A. 𝑦 = −4𝑥 − 1
B. 𝑦 = −4𝑥 + 1
C. 𝑦 = 4𝑥 − 1
D. 𝑦 = 4𝑥 +1
▶️Answer/Explanation
Ans: C
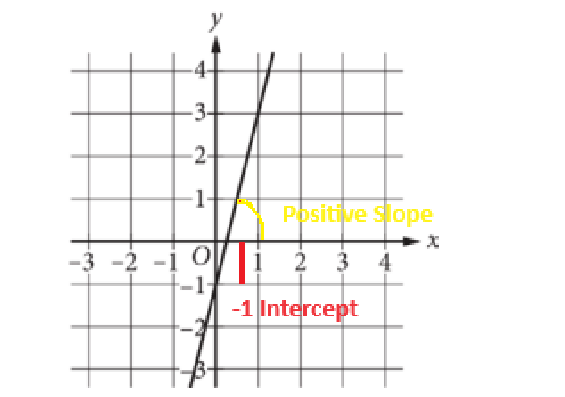
Which is only Option C .
[Calc] Question Easy

For the linear function f, the table shows three values of x and their corresponding values of 𝑓(𝑥). Which equation defines f?
A. 𝑓(𝑥) = −4𝑥 + 13
B. 𝑓(𝑥) = −2𝑥 + 13
C. \(f(x)=-\frac{5}{2}x+13\)
D. \(f(x)=-\frac{2}{5}x+13\)
▶️Answer/Explanation
Ans: D
Given the table with three values of \( x \) and their corresponding values of \( f(x) \), we need to find the linear function \( f(x) \). We’ll use the slope-intercept form of a linear equation: \( f(x) = mx + b \), where \( m \) is the slope and \( b \) is the y-intercept.
We can calculate the slope using two points from the table:
\[ m = \frac{{f(x_2) – f(x_1)}}{{x_2 – x_1}} \]
Let’s use the points (0, 13) and (10, 9):
\[ m = \frac{{9 – 13}}{{10 – 0}} = \frac{{-4}}{{10}} = -\frac{2}{5} \]
Now, we can plug the slope into the slope-intercept form and use one of the points to find the y-intercept:
\[ f(x) = -\frac{2}{5}x + b \]
Using the point (0, 13):
\[ 13 = -\frac{2}{5}(0) + b \]
\[ b = 13 \]
So, the equation defining \( f \) is \( f(x) = -\frac{2}{5}x + 13 \). The correct answer is option D.
[Calc] Question Easy
The function f is defined by f(x) = \(\frac{9}{2} x + 1\). What is the slope of the graph of y = f(x) in the xy-plane?
A ) \(\frac{-9}{2}\)
B) \(\frac{-2}{9}\)
C) \(\frac{2}{9}\)
D) \(\frac{9}{2}\)
▶️Answer/Explanation
Ans: \(\frac{9}{2}\)
Given the function \( f(x) = \frac{9}{2} x + 1 \), we need to determine the slope of the graph of \( y = f(x) \) in the \(xy\)-plane.
The function \( f(x) \) is in the form \( y = mx + b \), where \( m \) is the slope.
Here, \( f(x) = \frac{9}{2} x + 1 \).
Thus, the slope \( m \) is \( \frac{9}{2} \).
[Calc] Question Easy
What is the graph of y = 3x + 4 ?

▶️Answer/Explanation
C
The given equation of the line is \( y = 3x + 4 \). This is in the slope-intercept form \( y = mx + b \), where \( m \) is the slope and \( b \) is the y-intercept.
1. Y-Intercept:
The y-intercept is the point where the line crosses the y-axis. This occurs when \( x = 0 \).
Substitute \( x = 0 \) into the equation:
\[
y = 3(0) + 4 = 4
\]
Therefore, the y-intercept is \( (0, 4) \).
2. X-Intercept:
The x-intercept is the point where the line crosses the x-axis. This occurs when \( y = 0 \).
Substitute \( y = 0 \) into the equation and solve for \( x \):
\[
0 = 3x + 4
\]
\[
3x = -4
\]
\[
x = -\frac{4}{3}
\]
Therefore, the x-intercept is \( \left( -\frac{4}{3}, 0 \right) \).
Which is only in graph – C
[Calc] QuestionEasy
Which of the following could represent the graph of the linear equation y = mx + 3, where m is a positive constant?

▶️Answer/Explanation
C
Since m is positive so lets find x and y intercept
for x intercept put y =0 $x=\frac{-3}{m}$ means x is negative
for y intercept put x =0$y=3$
Considering both intercept only option C is correct fit.
[Calc] Question Easy
The function g is defined by g(x) = 4x − 2. What is the value of g(−3) ?
A) \(\frac{-1}{4}\)
B) \(\frac{-5}{4}\)
C) -10
D) -14
▶️Answer/Explanation
D) -14
The function \(g\) is defined by \(g(x) = 4x – 2\). We need to find the value of \(g(-3)\).
Substitute \(x = -3\) into the function:
\[ g(-3) = 4(-3) – 2 \]
\[ g(-3) = -12 – 2 \]
\[ g(-3) = -14 \]
[Calc] Question Easy
The function f is defined by f(x) = 2x − 4. What is the y-intercept of the graph of y = f(x) in the xy-plane?
A)(0, 4)
B)(0, 2)
C)(0, −2)
D)(0, −4)
▶️Answer/Explanation
D)(0, −4)
The function \(f\) is defined by \(f(x) = 2x – 4\). To find the \(y\)-intercept of the graph of \(y = f(x)\), we set \(x = 0\) and solve for \(y\):
\[ y = 2(0) – 4 \]
\[ y = -4 \]
So, the \(y\)-intercept is \((0, -4)\).
The correct answer is D) (0, -4).
[No calc] Questions Easy
From 1990 to 2001, German currency included coins called pfennigs, worth 1 pfennig each, and groschen, worth 10 pfennigs each. Which equation represents the number of pfennig coins, p, and groschen coins,
g, that have a combined value of 85 pfennigs?
A) p+g=85
B) p+10g=85
C) 10p+g=85
D) 10(p+g)=85
▶️Answer/Explanation
Ans: B
Let \(p\) be the number of pfennig coins and \(g\) be the number of groschen coins.
Since each pfennig coin is worth \(1\) pfennig and each groschen coin is worth \(10\) pfennigs, the total value equation is:
\[1p + 10g = 85\]
So, the equation representing the number of pfennig coins, \(p\), and groschen coins, \(g\), that have a combined value of \(85\) pfennigs is B) \(p + 10g = 85\).
[No calc] Questions Easy
The function h is defined by \(h(x)=-\frac{1}{4}x-2\). Which is the graph of y =h(x)?

▶️Answer/Explanation
Ans: D
To find the \(x\)-intercept, we set \(h(x) = 0\) and solve for \(x\).
Given \(h(x) = -\frac{1}{4}x – 2\), when \(h(x) = 0\):
\[0 = -\frac{1}{4}x – 2\]
Adding \(2\) to both sides:
\[2 = -\frac{1}{4}x\]
Multiplying both sides by \(-4\) to isolate \(x\):
\[-8 = x\]
So, the \(x\)-intercept is \((-8, 0)\).
To find the \(y\)-intercept, we set \(x = 0\) and solve for \(y\).
Given \(h(x) = -\frac{1}{4}x – 2\), when \(x = 0\):
\[h(0) = -\frac{1}{4}(0) – 2\]
\[h(0) = -2\]
So, the \(y\)-intercept is \((0, -2)\).
From this Option – D is correct
[Calc] Question Easy

The table shows some values of x and their corresponding values of y. There is a linear relationship between x and y. Which of the following equations represents this relationship ?
A) \(y = \frac{1}{2}x +2\)
B) \(y = \frac{1}{2}x -2\)
C) y =2x+ 4
D) y =2x- 4
▶️Answer/Explanation
C) y =2x+ 4
To find the equation that represents the linear relationship between \(x\) and \(y\), we need to determine the slope (\(m\)) and the y-intercept (\(b\)) of the line \(y = mx + b\).
1. Calculate the slope (\(m\)):
The slope can be calculated using the formula:
\[ m = \frac{y_2 – y_1}{x_2 – x_1} \]
Using the first two points from the table, \((x_1, y_1) = (5, 14)\) and \((x_2, y_2) = (10, 24)\):
\[ m = \frac{24 – 14}{10 – 5} = \frac{10}{5} = 2 \]
2. Determine the y-intercept (\(b\)):
We can use one of the points and the slope to find the y-intercept. Using the point \((5, 14)\):
\[ y = mx + b \]
\[ 14 = 2(5) + b \]
\[ 14 = 10 + b \]
\[ b = 14 – 10 \]
\[ b = 4 \]
So, the equation of the line is:
\[ y = 2x + 4 \]
[Calc] Questions Easy
Dana is riding in a 100-mile-long bicycle race. The function f defined by f(x) =100-18x models the number of miles that Dana has remaining x hours after she starts the race. What is the best interpretation of f(2) = 64 ?
A) Dana rides about 64 miles in the first 2 hours of the race.
B) Dana will ride the last 64 miles of the race in about 2 hours.
C) When Dana has ridden 64 miles, she has about 2 hours remaining.
D) Two hours after Dana starts the race, she has about 64 miles remaining.
▶️Answer/Explanation
Ans: D
To interpret \(f(2) = 64\) in the context of the given function \(f(x) = 100 – 18x\), where \(x\) represents the number of hours after Dana starts the race:
Substitute \(x = 2\) into the function:
\[f(2) = 100 – 18(2)\]
\[f(2) = 100 – 36\]
\[f(2) = 64\]
This means that when \(x = 2\), Dana has 64 miles remaining in the race.
So, the best interpretation of \(f(2) = 64\) is \(\mathbf{D}\).
[Calc] Questions Easy
How many solutions does the equation | x+7| =- 4 have?
A) Zero
B) Exactly one
C) Exactly two
D) More than two
▶️Answer/Explanation
Ans: A
The equation \(|x+7|=-4\) represents the absolute value of \(x+7\), which cannot be negative. Since the absolute value of any real number is always non-negative, the equation \(|x+7|=-4\) has no solutions. So, the correct answer is \(\mathbf{A}\) – Zero solutions.
Questions
The graph of $y=f(x)$ is a line in the $x y$-plane that passes through the point $(0,2)$ and has a slope of 5 . Which of the following equations could define the function $f$ ?
A. $f(x)=-\frac{1}{2} x+5$
B. $f(x)=-\frac{1}{5} x+2$
C. $f(x)=2 x+5$
D. $f(x)=5 x+2$
▶️Answer/Explanation
Ans: D
Question
Tony spends $\$ 80$ per month on public transportation. A 10-ride pass costs $\$ 12.50$, and a single-ride pass costs $\$ 1.50$. If $g$ represents the number of 10-ride passes Tony buys in a month and $t$ represents the number of single-ride passes Tony buys in a month, which of the following equations best represents the relationship between $g$ and $t$ ?
A. $g+t=80$
B. $g+t=1.50+12.50$
C. $1.50 \mathrm{~g}+12.50 t=80$
D. $12.50 g+1.50 t=80$
▶️Answer/Explanation
Ans: D
Questions
$a x=5$ In the equation above, $a$ is a constant. For which of the following values of $a$ will the equation have no solution?
A. 0
B. 1
C. 5
D. 10
▶️Answer/Explanation
Ans: A
Questions

For the linear function \(h\), the table above shows several values of \(x\) and their corresponding values of \(h(x)\). Which of the following defines \(h\)?
- \(h(x)=2x-3\)
- \(h(x)=3x-5\)
- \(h(x) = 4x – 7\)
- \(h(x) = 4x-9\)
▶️Answer/Explanation
Ans: B
Questions
A care-sharing service charges $\$ 6$ per hour to rent a car plus a $\$ 10$ fee for insurance. Which of the following gives the total cost $c$, in dollars, of a rental that lasts $t$ hours?
A. $c=6 t+10$
B. $c=6 t-10$
C. $c=10 t+6$
D. $c=16 t$
▶️Answer/Explanation
Ans: A
Questions
$2(x+b)=a x+c$ In the equation above, $a, b$, and $c$ are constants. If the equation has infinitely many solutions, which of the following must be equal to $c$ ?
A. $a$
B. $b$
C. $2 a$
D. $2 b$
▶️Answer/Explanation
Ans: D
Question
The hardcover books produced by a publisher have pages that are 0.1 millimeter thick and a front cover and a back cover that each are 2 millimeters thick. Which of the following gives the total thickness $f(n)$, in millimeters, of a closed book that has $n$ pages?
A. $f(n)=4+0.1 n$
B. $f(n)=2+0.1 n$
C. $f(n)=0.4+0.1 n$
D. $f(n)=0.2+0.1 n$
▶️Answer/Explanation
Ans: A
Question
The pressure exerted on an object under water increases by 1 atmosphere every 33 feet below the surface of the water. At sea level, the pressure is 1 atmosphere. Which equation gives the total pressure $p$, in atmospheres, exerted on an underwater object at a depth of $f$ feet below sea level?
A. $p=\frac{f}{33}$
B. $p=33 f$
C. $p=33 f+1$
D. $p=\frac{f}{33}+1$
▶️Answer/Explanation
Ans: D
Question
For each repair job, an elevator technician charges $r$ dollars per hour for each hour worked plus a flat fee of $k$ dollars. If the technician charges $\$ 210$ for a 2-hour job, which of the following represents the relationship between $r$ and $k$ ?
A. $210=k+2 r$
B. $210=2 k+r$
C. $210=2 r-k$
D. $210=r-2 k$
▶️Answer/Explanation
Ans: A
Question
The sum of two different numbers $x$ and $y$ is 70 and the difference when the smaller number is subtracted from the larger number is 30 . What is the value of $x y$ ?
A. 100
B. 210
C. 1,000
D. 2,100
▶️Answer/Explanation
Ans: C
Question
$C=10 x+4 y$
The formula above gives the monthly cost $C$, in dollars, of operating a delivery truck when the driver works a total of $x$ hours and when $y$ gallons of gasoline are used. If, in a particular month, it cost no more than $\$ 2,000$ to operate the truck and at least 150 gallons of gas were used, what is the maximum number of hours the driver could have worked?
A. 125
B. 140
C. 500
D. 1,400
▶️Answer/Explanation
Ans: B