SAT MAth Practice questions – all topics
- Algebra Weightage: 35% Questions: 13-15
- Linear equations in one variable
- Linear equations in two variables
- Linear functions
- Systems of two linear equations in two variables
- Linear inequalities in one or two variables
SAT MAth and English – full syllabus practice tests
[Calc] Question Easy
\[
\begin{aligned}
& 5 x+3 y=7 \\
& 2 x+y=2
\end{aligned}
\]
The solution to the given system of equations is \((x, y)\). What is the value of \(7 x+4 y\) ?
A) 2
B) 7
C) 9
D) 23
▶️Answer/Explanation
Ans:C
We need to find the value of \( 7x + 4y \) for the system of equations:
\[
\begin{aligned}
& 5x + 3y = 7 \quad \text{(1)} \\
& 2x + y = 2 \quad \text{(2)}
\end{aligned}
\]
First, solve the system of equations to find \(x\) and \(y\).
Multiply equation (2) by 3 to align the coefficients of \(y\):
\[
3(2x + y) = 3 \cdot 2 \\
6x + 3y = 6 \quad \text{(3)}
\]
Subtract equation (1) from equation (3):
\[
(6x + 3y) – (5x + 3y) = 6 – 7 \\
x = -1
\]
Now substitute \(x = -1\) back into equation (2) to find \(y\):
\[
2(-1) + y = 2 \\
-2 + y = 2 \\
y = 4
\]
Now, we have the solution \( (x, y) = (-1, 4) \).
Next, calculate \(7x + 4y\):
\[
7x + 4y = 7(-1) + 4(4) \\
7x + 4y = -7 + 16 \\
7x + 4y = 9
\]
[Calc] Question Easy
A company decides to sponsor an employee bowling team. The cost to form the team is \(\$ 180\) per team member plus a onetime \(\$ 25\) team-registration fee. What is the maximum number of team members who can join the team, if the company can spend \(\$ 925\) for the bowling team?
▶️Answer/Explanation
Ans:5
To find the maximum number of team members who can join the bowling team, we need to consider the total cost for the team and the budget available.
Each team member costs \(\$180\) and there is a one-time \(\$25\) team-registration fee. Let \(n\) be the number of team members. Then, the total cost for \(n\) team members is given by:
Total Cost = Cost per team member × Number of team members + Team-registration fee
\[ \text{Total Cost} = 180n + 25 \]
We know that the company can spend \(\$925\) for the bowling team. So, we can set up the equation:
\[ 180n + 25 \leq 925 \]
Now, we solve for \(n\):
\[ 180n \leq 925 – 25 \]
\[ 180n \leq 900 \]
\[ n \leq \frac{900}{180} \]
\[ n \leq 5 \]
So, the maximum number of team members who can join the team is \(5\). Therefore, the correct answer is \(5\).
[Calc] Question Easy
The mass \(y\), in grams, of juvenile cobia fish \(x\) days after hatching can be modeled by the equation \(y=-324+5.6 x\), where \(60 \leq x \leq 100\). Which graph represents this relationship?
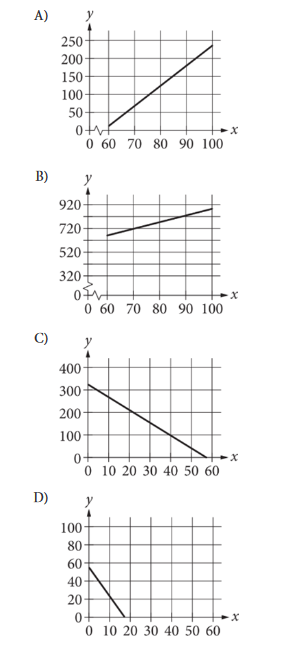
▶️Answer/Explanation
A
For \(\mathrm{x}=60\) :
\(
\begin{aligned}
& y=-324+5.6(60) \\
& y=-324+336 \\
& y=12
\end{aligned}
\)
\(\begin{aligned} & \text { For } x=100: \\ & y=-324+5.6(100) \\ & y=-324+560 \\ & y=236\end{aligned}\)
[Calc] Question Easy
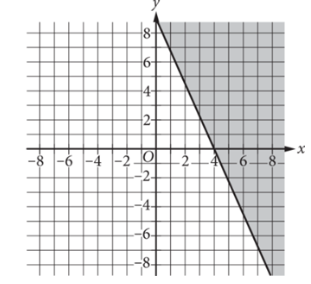
The shaded region shown represents all solutions to an inequality. Which ordered pair \((x, y)\) is a solution to this inequality?
A) \((5,0)\)
B) \((0,5)\)
C) \((-5,0)\)
D) \((0,-5)\)
▶️Answer/Explanation
A
Option A lie in the Shaded region
[Calc] Questions Foundation
$
f(x)=-0.5 x+56
$
The given function models the average daily temperature \(f(x)\), in degrees Fahrenheit \(\left({ }^{\circ} \mathrm{F}\right)\), in Chicago \(x\) days after November 1 , for \(0 \leq x \leq 29\). Based on this model, what is the average daily temperature, in \({ }^{\circ} \mathrm{F}\), in Chicago 6 days after November 1 ?
A) 62
B) 60
C) 56
D) 53
▶️Answer/Explanation
Ans:D
To find the average daily temperature \(f(x)\) 6 days after November 1, we need to evaluate the given function \(f(x) = -0.5x + 56\) at \(x = 6\).
Substitute \(x = 6\) into the function:
\[
f(6) = -0.5(6) + 56
\]
\[
f(6) = -3 + 56
\]
\[
f(6) = 53
\]
So, the average daily temperature in Chicago 6 days after November 1 is \(53^\circ \mathrm{F}\).
[No calc] Questions Easy
$y>4x$
$y \leq- x$
When graphed in the xy-plane, what point (x, y) is a solution to the given system of inequalities?
A) (1,1)
B) (-2,-2)
C) (3,-3)
D) (-4,4)
▶️Answer/Explanation
Ans: B
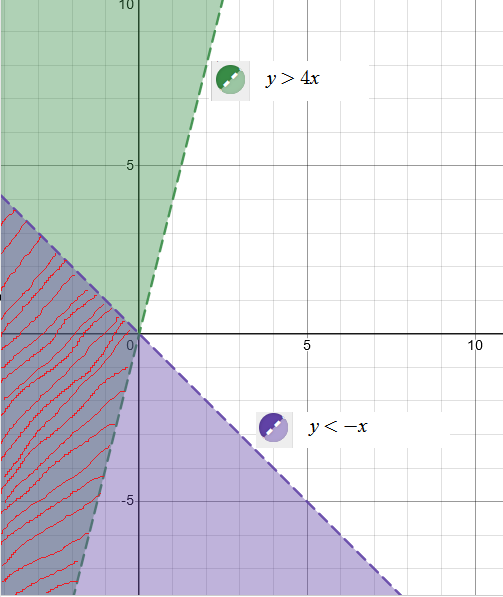
Common areas of intersection will be second and third quadrant.
\[
\begin{aligned}
& \text { Option A: }(1,1) \\
& y>4 x \\
& 1>4(1)=4 \text { (False) } \\
& y \leq x \\
& 1 \leq 1 \text { (True) }
\end{aligned}
\]
Since the point \((1,1)\) satisfies only one inequality, it is not a solution to the system.
\[
\begin{aligned}
& \text { Option B: }(-2,-2) \\
& y>4 x \\
& -2>4(-2)=-8 \text { (True) } \\
& y \leq x \\
& -2 \leq-2 \text { (True) }
\end{aligned}
\]
The point \((-2,-2)\) satisfies both inequalities, so it is a solution to the system.
Option C: \((3,-3)\)
\[
\begin{aligned}
& y>4 x \\
& -3>4(3)=12 \text { (False) } \\
& y \leq x \\
& -3 \leq 3 \text { (False) }
\end{aligned}
\]
The point \((3,-3)\) does not satisfy either inequality, so it is not a solution.
\[
\begin{aligned}
& \text { Option D: }(-4,4) \\
& y>4 x \\
& 4>4(-4)=-16 \text { (True) } \\
& y \leq x \\
& 4 \leq-4 \text { (False) }
\end{aligned}
\]
The point \((-4,4)\) satisfies only one inequality, so it is not a solution.
Therefore, the correct option is B) \((-2,-2)\).
[Calc] Question Easy
Aracely can spend up to a total of $\$ 20$ on streamers and balloons for a party. Streamers cost $\$ 1.49$ per pack, and balloons cost $\$ 4.39$ per pack. Which of the following inequalities represents this situation, where $s$ is the number of packs of streamers Aracely can buy, and $b$ is the number of pack of balloons Aracely can buy? (Assume there is no sales tax.)
A) $1.49 s-4.39 b \leq 20$
B) $1.49 s+4.39 b \leq 20$
C) $1.49 s-4.39 b \geq 20$
D) $1.49 s+4.39 b \geq 20$
▶️Answer/Explanation
B
Question
f (t) = 0.025t + 10.30 The function f models the length f(t) , in micrometers, of a yeast cell of a certain strain t minutes after completing cell division for 0 ≤ t ≤ 30
What is the predicted length, rounded to the nearest tenth of a micrometer, of a yeast cell 10 minutes after completing cell division?
- 10.1
- 10.3
- 10.6
- 12.8
▶️Answer/Explanation
C
Question
f (t) = 0.025t + 10.30 The function f models the length f(t) , in micrometers, of a yeast cell of a certain strain t minutes after completing cell division for 0 ≤ t ≤ 30
What is the best interpretation of the number 0.025 in the context of this model?
- The predicted length, in micrometers, of a yeast cell before cell division starts.
- The predicted length, in micrometers, of a yeast cell each minute after completing cell division.
- The increase in the predicted length, in micrometers, of a yeast cell every 10.3 minutes after completing cell division.
- The increase in the predicted length, in micrometers, of a yeast cell each minute after completing cell division.
▶️Answer/Explanation
D
Questions
Jonathan needs to earn at least $\$ 175$ next week and can work at most 20 hours. He earns $\$ 10$ per hour at his lawn service job and $\$ 8$ per hour at his job at the gym. Which of the following systems of inequalities represents this situation in terms of the number of hours he will work at his lawn service job, $l$, and the number of hours he will work at his job at the gym, $g$, next week?
A.
$10 l+8 g \leq 175$
$l+g \leq 20$
B.
$10 l+8 g \leq 175$
$l+g \geq 20$
C.
$10 l+8 g \geq 175$
$l+g \leq 20$
D.
$10 l+8 g \geq 20$
$l+g \geq 175$
▶️Answer/Explanation
Ans: C
Question
A gravel company had 30 tons of gravel in stock at the end of the day on Monday. On Tuesday the company shipped 10 tons of gravel and received no deliveries. On Wednesday the company made no shipments and received a delivery of 20 tons of gravel. On Thursday the company made no shipments and received no deliveries. On Friday the company shipped 20 tons of gravel and received no deliveries. Which of the following represents the number of tons of gravel the company had in stock at the end of each day?
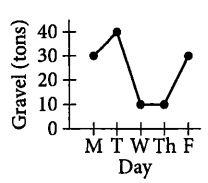
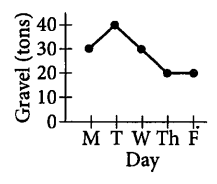
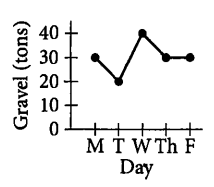
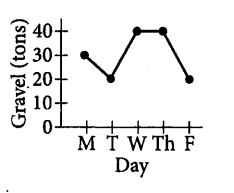
▶️Answer/Explanation
Ans: D
Questions
The Conowingo Reservoir had an original storage capacity of300,000 acre-feet at the end of 1928, the year in which it was built. Starting in 1929, sediment carried downstream by the Susquehanna River collected in the reservoir and began reducing the reservoir’s storage capacity at the approximate rate of 1,700 acre-feet per year.
If the reservoir’s capacity $t$ years after 1928 was between 290,000 and 292,000 acre-feet, which of the following must be true?
A. $t<2$
B. $2<t<4$
C. $4<t<6$
D. $6<t<8$
▶️Answer/Explanation
Ans: C
Questions
$y \geq-2 x+11$
$
y>3 x-9
$
In the $x y$-plane, point $A$ is contained in the graph of the solution set of the system of inequalities above. Which of the following could be the coordinates of point $A$ ?
A. $(2,1)$
B. $(4,1)$
C. $(4,5)$
D. $(6,6)$
▶️Answer/Explanation
Ans: C
Question
$g(t)=\frac{5(7 t-12 c)}{2}-25$
The number of people who go to a public swimming pool can be modeled by the function $g$ above, where $c$ is a constant and $t$ is the air temperature in degrees Fahrenheit $\left({ }^{\circ} \mathrm{F}\right.$ ) for $70<t<100$. If 350 people are predicted to go to the pool when the temperature is $90^{\circ} \mathrm{F}$, what is the value of $c$ ?
A. 20
B. 40
C. 60
D. 80
▶️Answer/Explanation
Ans: B
Question
At the beginning of a laboratory experiment, Miguel had 10 milliliters of a solution in a flask. The first step of the experiment consisted of Miguel pouring $x$ milliliters of the solution into a beaker and $y$ milliliters of the solution into a different beaker. There remained at least 4 milliliters of the solution in the flask after the first step. Which of the following inequalities can be used to correctly represent this situation?
A. $10-x-y \geq 4$
B. $10-x+y \geq 4$
C. $4-x-y \geq 5$
D. $4-x+y \geq 5$
▶️Answer/Explanation
Ans: A