Digital SAT Math: systems of Non linear equations in two variables-Practice Questions

SAT MAth Practice questions – all topics

Advanced Math Weightage: 35% Questions: 13-15
- Equivalent expressions
- Nonlinear equations in one variable and systems of equations in two variables
- Nonlinear functions

SAT MAth and English – full syllabus practice tests

[Calc] Questions Easy

What is the y-coordinate of the y-intercept of the graph of $y=3^{x}+9$ ?

▶️Answer/Explanation

Ans: 10

To find the $y$-coordinate of the $y$-intercept of the graph of $y = 3^x + 9$, we set $x = 0$ and solve for $y$:

\[y = 3^0 + 9 = 1 + 9 = 10\]

So, the $y$-coordinate of the $y$-intercept is $10$.

Question

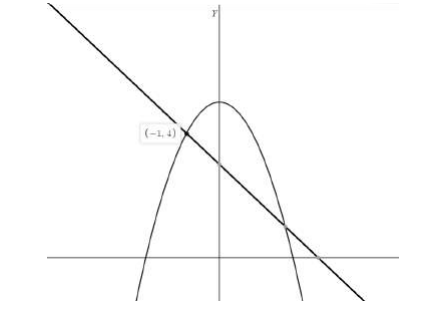
The graph of a linear equation and the graph of a quadratic equation are shown. What is true about the point (−1,4)?

The point satisfies only the quadratic equation
The point satisfies only the linear equation.
The point satisfies both equations.
The point satisfies neither equation.

Answer/Explanation

Ans: C

Question

$y=(x+3)(x-7)$
$y=x-7$
If $(x,y)$ is a solution to the given system of equations, which of the following could be the value of $x$?

-7
-3
3
7

Answer/Explanation

Ans: D

Question

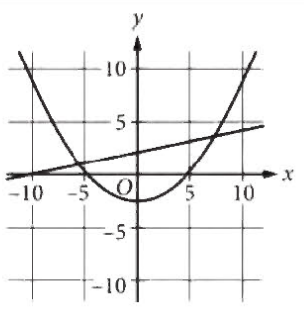
A system of equations consists of a quadratic equation and a linear equation. The equations in this system are graphed in the $xy$-plane above. How many solutions does the system have?

Answer/Explanation

Ans: C

Question

In the $xy$-plane, a parabola has vertex (3, 1) and intersects the $x$-axis at two points. If the equation of the parabola is written in the form $y = ‐ax^2 +bx + c$, where $a, b$, and $c$ are constants, which of the following could be a value of $c$?

-8
2
3
7

Answer/Explanation

Ans: A

Question

In the $xy$-plane, what is the $y$-coordinate of the point of intersection of the graphs of $y = (x ‐ 1)^2$ and $y = 2x ‐ 3$?

Answer/Explanation

Ans: 1

Question

$x-y=1$
$x+ y=x^2 -3$
Which ordered pair is a solution to the system of equations above?

$(1+\sqrt{3},3)$
$(\sqrt{3},-\sqrt{3})$
$(1+\sqrt{5},\sqrt{5})$
$(\sqrt{5},-1+\sqrt{5})$

Answer/Explanation

Ans: A

Question

$(x+2)^2+(y-3)^2=40$

$y=-2x+4$

Which of the following could be the $x$-coordinate of a solution to the system of equations above?

$\sqrt{7}$
$\frac{\sqrt{35}}{2}$
$\frac{6+2\sqrt{34}}{5}$
$\frac{4+\sqrt{191}}{5}$

Answer/Explanation

Ans: A

Question

$E = 18,000 – 2,000t$

$V = 18,000(0.85^{t})$
The given equations are two different models that can be used to find the value, in dollars, of a particular car $t$ years after it was purchased. Which of the following statements correctly compares the values of $E$ and $V$ for $O < t < 9$ ?

$E$ is always less than $V$.
$E$ is always greater than $V$.
$E$ is initially greater than $V$ but eventually becomes less than $V$.
$E$ is initially less than $V$ but eventually becomes greater than $V$.

▶️Answer/Explanation

Question

Kao measured the temperature of a cup of hot chocolate placed in a room with a constant temperature of70 degrees Fahrenheit ( $\left.{ }^{\circ} \mathrm{F}\right)$. The temperature of the hot chocolate was $185^{\circ} \mathrm{F}$ at 6:00 p.m. when it started cooling. The temperature of the hot chocolate was 156 $6^{\circ} \mathrm{F}$ at 6:05 p.m. and $135^{\circ} \mathrm{F}$ at 6:10 p.m. The temperature of the hot chocolate continued to decrease. Of the following functions, which best models the temperature $T(m)$, in degrees Fahrenheit, of Kao’s hot chocolate $m$ minutes after it started cooling?
A. $T(m)=185(1.25)^m$
B. $T(m)=185(0.85)^m$
C. $T(m)=(185-70)(0.75)^{\frac{m}{5}}$
D. $T(m)=70+115(0.75)^{\frac{m}{5}}$

▶️Answer/Explanation

Ans: D