| Marks available | 4 |
| Reference code | 10M.2.hl.TZ1.3 |
Question
Chloroethene, C2H3Cl, is an important organic compound used to manufacture the polymer poly(chloroethene).
State an equation for the reaction of ethanoic acid with water.
Calculate the pH of \({\text{0.200 mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) ethanoic acid \(({\text{p}}{K_{\text{a}}} = 4.76)\).
Determine the pH of a solution formed from adding \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{1.00 mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) ethanoic acid, \({\text{C}}{{\text{H}}_{\text{3}}}{\text{COOH(aq)}}\), to \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.600 mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) sodium hydroxide, NaOH(aq).
(if acid added) \({\text{C}}{{\text{H}}_3}{\text{CO}}{{\text{O}}^ – } + {{\text{H}}^ + } \to {\text{C}}{{\text{H}}_3}{\text{COOH}}\);
(if alkali added) \({\text{C}}{{\text{H}}_3}{\text{COOH}} + {\text{O}}{{\text{H}}^ – } \to {\text{C}}{{\text{H}}_3}{\text{CO}}{{\text{O}}^ – } + {{\text{H}}_2}{\text{O}}\);
Explanation marks cannot be awarded without equations.
Markscheme
\({\text{C}}{{\text{H}}_3}{\text{COOH(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{C}}{{\text{H}}_3}{\text{CO}}{{\text{O}}^ – }{\text{(aq)}} + {{\text{H}}_3}{{\text{O}}^ + }{\text{(aq)}}\);
OR
\({\text{C}}{{\text{H}}_3}{\text{COOH(l)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{C}}{{\text{H}}_3}{\text{CO}}{{\text{O}}^ – }{\text{(aq)}} + {{\text{H}}_3}{{\text{O}}^ + }{\text{(aq)}}\);
OR
\({\text{C}}{{\text{H}}_3}{\text{COOH(aq)}} \rightleftharpoons {\text{C}}{{\text{H}}_3}{\text{CO}}{{\text{O}}^ – }{\text{(aq)}} + {{\text{H}}^ + }{\text{(aq)}}\);
Must include \( \rightleftharpoons \).
Ignore state symbols.
(ii) \({K_{\text{a}}} = {10^{ – 4.76}}/1.74 \times {10^{ – 5}}/{\text{pH}} = {\text{p}}{K_{\text{a}}} + \log \frac{{{\text{[SALT]}}}}{{{\text{[ACID]}}}}\);
\(1.74 \times {10^{ – 5}} = \frac{{{{{\text{[}}{{\text{H}}^ + }{\text{]}}}^2}}}{{{\text{0.200}}}}/{\text{[}}{{\text{H}}^ + }{\text{]}} = 0.00187\);
\({\text{pH}} = 2.73\);
Award [3] for correct final answer, allow mark for correct conversion of [H+] to pH even if [H+] incorrect.
(initial) \({\text{[C}}{{\text{H}}_{\text{3}}}{\text{COOH]}} = 0.500{\text{ mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) and) eqm \({\text{[C}}{{\text{H}}_{\text{3}}}{\text{COOH]}} = 0.200{\text{ mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\);
(initial) \({\text{[C}}{{\text{H}}_{\text{3}}}{\text{CO}}{{\text{O}}^ – }{\text{]}} = 0.300{\text{ mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) and) eqm \({\text{[C}}{{\text{H}}_{\text{3}}}{\text{CO}}{{\text{O}}^ – }{\text{]}} = 0.300{\text{ mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\);
Allow 0.02 moles and 0.03 moles instead of 0.200 and 0.300.
\({\text{[}}{{\text{H}}^ + }{\text{]}} = {K_{\text{a}}}\frac{{{\text{[C}}{{\text{H}}_3}{\text{COOH]}}}}{{{\text{[C}}{{\text{H}}_3}{\text{CO}}{{\text{O}}^ – }{\text{]}}}} = 1.16 \times {10^{ – 5}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\);
\({\text{pH}} = 4.94\);
Award [3 max] for correct final answer if no working shown.
Examiners report
The only issue was that some candidates forgot the reversible arrow in the equation.
A pleasing number were able to complete the pH calculation successfully.
Only the best candidates scored full marks for the buffer calculation; in some cases an incorrect expression was used, but more often there was no attempt to calculate the equilibrium amounts or concentrations.
There were very few who could write appropriate equations for the buffer action, even though it clearly stated that the answer should include equations many explained buffer action without any equations and scored no marks as a result.
| Marks available | 7 |
| Reference code | 10M.2.hl.TZ2.7 |
Question
Water is an important substance that is abundant on the Earth’s surface.
Buffer solutions resist small changes in pH. A phosphate buffer can be made by dissolving \({\text{Na}}{{\text{H}}_{\text{2}}}{\text{P}}{{\text{O}}_{\text{4}}}\) and \({\text{N}}{{\text{a}}_{\text{2}}}{\text{HP}}{{\text{O}}_{\text{4}}}\) in water, in which \({\text{Na}}{{\text{H}}_{\text{2}}}{\text{P}}{{\text{O}}_{\text{4}}}\) produces the acidic ion and \({\text{N}}{{\text{a}}_{\text{2}}}{\text{HP}}{{\text{O}}_{\text{4}}}\) produces the conjugate base ion.
A \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) ammonia solution is placed in a flask and titrated with a \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) hydrochloric acid solution.
(i) State the expression for the ionic product constant of water, \({K_{\text{w}}}\).
(ii) Explain why even a very acidic aqueous solution still has some \({\text{O}}{{\text{H}}^ – }\) ions present in it.
(iii) State and explain the effect of increasing temperature on the value of \({K_{\text{w}}}\) given that the ionization of water is an endothermic process.
(iv) State and explain the effect of increasing temperature on the pH of water.
(i) Deduce the acid and conjugate base ions that make up the phosphate buffer and state the ionic equation that represents the phosphate buffer.
(ii) Describe how the phosphate buffer minimizes the effect of the addition of a
strong base, \({\text{O}}{{\text{H}}^ – }{\text{(aq)}}\), to the buffer. Illustrate your answer with an ionic equation.
(iii) Describe how the phosphate buffer minimizes the effect of the addition of a
strong acid, \({{\text{H}}^ + }{\text{(aq)}}\), to the buffer. Illustrate your answer with an ionic equation.
(i) Explain why the pH of the ammonia solution is less than 13.
(ii) Estimate the pH at the equivalence point for the titration of hydrochloric acid with ammonia and explain your reasoning.
(iii) State the equation for the reaction of ammonia with water and write the \({K_{\text{b}}}\) expression for \({\text{N}}{{\text{H}}_{\text{3}}}{\text{(aq)}}\).
(iv) When half the ammonia has been neutralized (the half-equivalence point), the pH of the solution is 9.25. Deduce the relationship between \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) and \({\text{[NH}}_4^ + {\text{]}}\) at the
half-equivalence point.
(v) Determine \({\text{p}}{K_{\text{b}}}\) and \({K_{\text{b}}}\) for ammonia based on the pH at the half-equivalence point.
(vi) Describe the significance of the half-equivalence point in terms of its effectiveness as a buffer.
Markscheme
(i) \({\text{(}}{K_{\text{w}}}{\text{)}} = {\text{[}}{{\text{H}}^ + }{\text{][O}}{{\text{H}}^ – }{\text{] / (}}{K_{\text{w}}}{\text{)}} = {\text{[}}{{\text{H}}_{\text{3}}}{{\text{O}}^ + }{\text{][O}}{{\text{H}}^ – }{\text{]}}\);
Do not award mark if [ ] omitted or other brackets are used.
(ii) \({\text{[}}{{\text{H}}^ + }{\text{]}}\) increases, \({\text{[O}}{{\text{H}}^ – }{\text{]}}\) decreases but still some present (\({K_{\text{w}}}\) constant) / \({\text{[O}}{{\text{H}}^ – }{\text{]}}\) cannot go to zero as equilibrium present / \({\text{[O}}{{\text{H}}^ – }{\text{]}} = \frac{{{K_{\text{w}}}}}{{{\text{[}}{{\text{H}}^ + }{\text{]}}}}\), thus \({\text{[O}}{{\text{H}}^ – }{\text{]}}\) cannot be zero / OWTTE;
Accept equilibrium present.
(iii) (changing T disturbs equilibrium) forward reaction favoured / equilibrium shifts to the right;
to use up (some of the) heat supplied;
\({{K_{\text{w}}}}\) increases (as both \({{\text{[}}{{\text{H}}^ + }{\text{]}}}\) and \({\text{[O}}{{\text{H}}^ – }{\text{]}}\) increase);
(iv) (as \({{\text{[}}{{\text{H}}^ + }{\text{]}}}\) increases) pH decreases / \({\text{pH}} < 7\);
No mark for more acidic.
inverse relationship between pH and \({\text{[}}{{\text{H}}^ + }{\text{] / pH}} = – \log {\text{[}}{{\text{H}}^ + }{\text{] / pH}} = {\log _{10}}\frac{{\text{1}}}{{{\text{[}}{{\text{H}}^ + }{\text{]}}}}\);
Accept [H3O+] in place of [H+].
(i) Acid: \({{\text{H}}_2}{\text{PO}}_4^ – \);
(Conjugate) base: \({\text{HPO}}_4^{2 – }\);
No mark for NaH2PO4 or Na2HPO4.
\({{\text{H}}_2}{\text{PO}}_4^ – {\text{(aq)}} \rightleftharpoons {{\text{H}}^ + }{\text{(aq)}} + {\text{HPO}}_4^{2 – }{\text{(aq)}}\);
Accept reverse equation or reaction with water.
Ignore state symbols, but equilibrium sign is required.
Accept OH– (ions) react with H+ (ions) to form H2O.
(ii) strong base/\({\text{O}}{{\text{H}}^ – }\) replaced by weak base (\({\text{HPO}}_4^{2 – }\), and effect minimized) / strong base reacts with acid of buffer / equilibrium in (i) shifts in forward direction;
Accept OH– added reacts with H+ to form H2O.
\({\text{O}}{{\text{H}}^ – }{\text{(aq)}} + {{\text{H}}_2}{\text{PO}}_4^ – {\text{(aq)}} \to {{\text{H}}_2}{\text{O(l)}} + {\text{HPO}}_4^{2 – }{\text{(aq)}}\);
Ignore state symbols, accept equilibrium sign.
(iii) strong acid/\({{\text{H}}^ + }\) replaced by weak acid (\({{\text{H}}_2}{\text{PO}}_4^ – \), and effect minimized) / strong acid reacts with base of buffer / equilibrium in (i) shifts in reverse direction;
\({{\text{H}}^ + }{\text{(aq)}} + {\text{HPO}}_4^{2 – }{\text{(aq)}} \to {{\text{H}}_2}{\text{PO}}_4^ – {\text{(aq)}}\);
Accept reaction with H3O+.
Ignore state symbols.
(i) \({\text{N}}{{\text{H}}_3}\) weak(er) base/partial dissociation;
\({\text{[O}}{{\text{H}}^ – }{\text{]}} < {\text{0.1(0)}}/{\text{pOH}} > 1{\text{ (thus pH}} < 13/{\text{pH}} + {\text{pOH}} = 14{\text{)}}\);
(ii) around \({\text{pH}} = 5\);
Accept a value between 4 and 6.
strong acid–weak base titration, (thus acidic) / at equivalence point, \({\text{NH}}_4^ + \) present is acidic / \({\text{NH}}_4^ + \rightleftharpoons {\text{N}}{{\text{H}}_3} + {{\text{H}}^ + }\);
(iii) \({\text{N}}{{\text{H}}_3}{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{NH}}_4^ + {\text{(aq)}} + {\text{O}}{{\text{H}}^ – }{\text{(aq)}}\);
Ignore state symbols, but equilibrium sign required.
\({K_{\text{b}}} = \frac{{{\text{[NH}}_4^ + {\text{][O}}{{\text{H}}^ – }{\text{]}}}}{{{\text{[N}}{{\text{H}}_3}{\text{]}}}}\);
(iv) \({\text{[N}}{{\text{H}}_3}{\text{]}} = {\text{[NH}}_4^ + {\text{]}}\);
(v) \({\text{pOH}} = 14.00 – 9.25 = 4.75\);
\({\text{p}}{K_{\text{b}}}{\text{ (}} = {\text{pOH)}} = 4.75\);
\({K_{\text{b}}} = 1.78 \times {10^{ – 5}}\);
Ignore units.
Award [3] for correct final answer.
(vi) optimum/most effective/highest buffer capacity/50%–50% buffer/equally effective as an acidic buffer and a basic buffer / OWTTE;
Examiners report
This was the second least commonly answered question. With the exception of the part on buffer chemistry where very few appreciated what was happening, the question was reasonably well done.
While many candidates gave the correct \({K_{\text{w}}}\) expression, it was not uncommon to either find the value of the constant or \({K_{\text{w}}} = {K_{\text{a}}} \times {K_{\text{b}}}\) given as the answers. A few included \({\text{[}}{{\text{H}}_{\text{2}}}{\text{O]}}\) in the expression. Candidates recognised that increasing the temperature shifts the equilibrium to the right, but most did not explain why, namely to use up some of the heat supplied.
Candidates generally concluded that formation of more \({{\text{H}}^ + }\) and \({\text{O}}{{\text{H}}^ – }\) ions gives a higher value of \({K_{\text{w}}}\). A significant number of candidates were able to state the effect of increasing temperature on the pH of water (it decreases) but failed to explain why. Some simply incorrectly stated that the pH would not change.
Many candidates gave the wrong formulas for the acid and the conjugate base ions of the buffer or offered \({\text{Na}}{{\text{H}}_{\text{2}}}{\text{P}}{{\text{O}}_{\text{4}}}\) and \({\text{N}}{{\text{a}}_{\text{2}}}{\text{HP}}{{\text{O}}_{\text{4}}}\) as the answers. Some candidates gave good answers about the effect of adding a small amount of a strong acid or a strong base, but they could not write correct equations to show these two effects.
Nearly all candidates correctly said that the ammonia solution is a weak base because of partial dissociation and \({\text{[O}}{{\text{H}}^ – }{\text{]}}\) would be less than 0.1 to give a pH less than 13. The majority of candidates correctly identified the pH around 4 – 6 because it is a titration between a strong acid and a weak base. When writing the equation for the reaction of ammonia and water some candidates did not write the equilibrium sign. The \({K_{\text{b}}}\) expression was correct in most cases. However, many did not recognise that at the half-equivalence point both the base and the conjugate acid concentrations are equal. The \({\text{p}}{K_{\text{b}}}\) and \({K_{\text{b}}}\) were correctly calculated from the pH of the solution by many candidates. However, most failed to realize that at the half-equivalence point the capacity of the buffer is optimum.
| Marks available | 5 |
| Reference code | 12N.2.hl.TZ0.3 |
Question
Buffer solutions are widely used in both chemical and biochemical systems.
Describe the composition of an acidic buffer solution.
Determine the pH of a buffer solution, correct to two decimal places, showing your working, consisting of 10.0 g of \({\text{C}}{{\text{H}}_{\text{3}}}{\text{COOH}}\) and 10.0 g of CH\(_3\)COONa in \({\text{0.250 d}}{{\text{m}}^{\text{3}}}\) of solution. \({K_{\text{a}}}\) for \({\text{C}}{{\text{H}}_{\text{3}}}{\text{COOH}} = 1.8 \times {10^{ – 5}}\) at 298 K.
Markscheme
(solution containing significant/equal amounts of a) weak acid and its salt / (solution containing) strong base to which excess of weak acid has been added / OWTTE;
Accept (solution containing) weak acid and conjugate base.
Do not accept descriptions with specific compounds alone (e.g. CH3COOH and CH3COONa) unless compounds are stated as weak acid and its salt.
Accept answer such as (solution containing) x mol of weak acid and \(\frac{1}{2}x\,mol\) of strong base.
\({M_{\text{r}}}{\text{(C}}{{\text{H}}_{\text{3}}}{\text{COOH)}} = 60.06\) and \({M_{\text{r}}}{\text{ C}}{{\text{H}}_3}{\text{COONa}} = 82.04\);
\({\text{[C}}{{\text{H}}_3}{\text{COOH]}} = 6.66 \times {10^{ – 1}}/0.666{\text{ mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\)
\({\text{[C}}{{\text{H}}_3}{\text{CO}}{{\text{O}}^ – }{\text{]}} = 4.88 \times {10^{ – 1}}/{\text{ }}0.488{\text{ mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\);
\({\text{[}}{{\text{H}}_3}{{\text{O}}^ + }{\text{]}}/{\text{[}}{{\text{H}}^ + }{\text{]}} = (1.8 \times {10^{ – 5}} \times 6.66 \times {10^{ – 1}})/4.88 \times {10^{ – 1}} = 2.46 \times {10^{ – 5}}/0.0000246{\text{ mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\);
\({\text{pH}} = \left( { – {\text{log[}}{{\text{H}}_3}{{\text{O}}^ + }{\text{]}} = – {\text{log(2.46}} \times {\text{1}}{{\text{0}}^{ – 5}}{\text{)}} = } \right){\text{ 4.61 (2dp)}}\);
Award [5] for correct final answer of pH = 4.61 with some working shown.
Award [2 max] for pH = 4.61 without any working at all shown.
Two decimal places are required for M5.
OR
\({M_{\text{r}}}{\text{(C}}{{\text{H}}_{\text{3}}}{\text{COOH)}} = 60.06\) and \({M_{\text{r}}}{\text{ C}}{{\text{H}}_3}{\text{COONa}} = 82.04\);
\({\text{[C}}{{\text{H}}_3}{\text{COOH]}} = 6.66 \times {10^{ – 1}}/0.666{\text{ mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\)
\({\text{[C}}{{\text{H}}_3}{\text{CO}}{{\text{O}}^ – }{\text{]}} = 4.88 \times {10^{ – 1}}/{\text{ }}0.488{\text{ mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\);
\({\text{pH}} = – {\text{log(1.8}} \times {\text{1}}{{\text{0}}^{ – 5}}{\text{)}} + {\text{log}}\frac{{{\text{[salt]}}}}{{{\text{[acid]}}}}\);
\( = \left( {4.74 + \log \frac{{0.488}}{{0.666}} = 4.74 – 0.135 = } \right){\text{ }}4.61{\text{ (2dp)}}\);
M4 can be scored even if not explicitly stated if M5 is correct based on previous values.
Award [5] for correct final answer of pH = 4.61 with some working shown.
Award [2 max] for pH = 4.61 without any working at all shown.
Two decimal places are required for M5.
Examiners report
This question was based on buffer solutions and was found to be quite challenging for candidates. In part (a), some candidates again failed to read the question, which asked for a description of an acidic buffer solution. Many did not state explicitly that a weak acid is involved (acid alone was not sufficient).
In part (b), only the best candidates scored all five marks. In addition to conceptual errors, there were also a number of transcription errors (molar mass and arithmetic errors). Candidates also were required to express their answer to two decimal places. A number of candidates used the Henderson-Hasselbalch equation, but often an incorrect equation was given.
| Marks available | 4 |
| Reference code | 14M.2.hl.TZ1.7 |
Question
An equilibrium exists between nitrosyl chloride, NOCl, nitrogen oxide, NO, and chlorine, \({\text{C}}{{\text{l}}_{\text{2}}}\).
\[{\text{2NOCl(g)}} \rightleftharpoons {\text{2NO(g)}} + {\text{C}}{{\text{l}}_2}{\text{(g)}}\]
\({\text{20.0 c}}{{\text{m}}^{\text{3}}}\) of hexane, \({{\text{C}}_{\text{6}}}{{\text{H}}_{{\text{14}}}}\), and \({\text{20.0 c}}{{\text{m}}^{\text{3}}}\) of pentan-1-ol, \({{\text{C}}_{\text{5}}}{{\text{H}}_{{\text{11}}}}{\text{OH}}\), were placed separately into two closed containers at 298 K and allowed to reach equilibrium.
Ammonia is a weak base.
(i) Deduce the equilibrium constant expression for this reaction.
(ii) Explain the effect on the position of equilibrium and the value of \({K_{\text{c}}}\) when pressure is decreased and temperature is kept constant.
(iii) 2.00 mol of NOCl was placed in a \({\text{1.00 d}}{{\text{m}}^{\text{3}}}\) container and allowed to reach equilibrium at 298 K. At equilibrium, 0.200 mol of NO was present. Determine the equilibrium concentrations of NOCl and \({\text{C}}{{\text{l}}_{\text{2}}}\), and hence calculate the value of \({K_{\text{c}}}\) at this temperature.
(iv) The value of \({K_{\text{c}}}\) is \(1.60 \times {10^{ – 5}}\) at 318 K. State and explain whether the forward reaction is exothermic or endothermic.
(i) Compare the two liquids in terms of their boiling points, enthalpies of vaporization and vapour pressures.
(ii) Explain your answer given for part (b)(i).
Calculate the pH of a \({\text{1.50 mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) solution of ammonia at 298 K to two decimal places, using Table 15 of the Data Booklet.
A buffer solution is made using \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.500 mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) hydrochloric acid, HCl (aq), and \({\text{20.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{1.50 mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) ammonia solution, \({\text{N}}{{\text{H}}_{\text{3}}}{\text{(aq)}}\).
Describe the meaning of the term buffer solution.
Determine the pH of the buffer solution at 298 K.
A \({\text{1.50 mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) solution of ammonia is added to \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of a \({\text{0.500 mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) hydrochloric acid solution in a titration experiment.
Calculate the total volume of the solution at the equivalence point.
Calculate the pH of the solution at the equivalence point, using Table 15 of the Data Booklet.
Identify a suitable indicator for this titration, using Table 16 of the Data Booklet.
Markscheme
(i) \(({K_{\text{c}}} = )\frac{{{\text{[C}}{{\text{l}}_2}{\text{(g)][NO(g)}}{{\text{]}}^2}}}{{{{{\text{[NOCl(g)]}}}^2}}}\);
Ignore state symbols.
(ii) equilibrium shifts to right as there are more moles (of gas) on product side;
no change to \({K_{\text{c}}}\) as it is a constant at fixed temperature / OWTTE;
(iii) \({\text{[NOCl(g)]}} = 1.80{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{)}}\);
\({\text{[C}}{{\text{l}}_2}{\text{(g)]}} = 0.100{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{)}}\);
\({K_{\text{c}}} = \left( {\frac{{0.100 \times {{(0.200)}^2}}}{{{{(1.80)}^2}}}} \right)1.23 \times {10^{ – 3}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{)}}\);
Award [3] for correct final answer.
(iv) exothermic as \({K_{\text{c}}}\) is lower at higher temperature;
(i) hexane has lower boiling point and enthalpy of vaporization than pentan-1-ol / OWTTE;
hexane has higher vapour pressure than pentan-1-ol / OWTTE;
(ii) hexane is non-polar / has only van der Waals’/London/dispersion forces / has weaker intermolecular forces than pentan-1-ol;
pentan-1-ol has hydrogen bonding between molecules;
\({\text{[O}}{{\text{H}}^ – }{\text{]}} = \sqrt {1.50 \times 1.78 \times {{10}^{ – 5}}} = 5.17 \times {10^{ – 3}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{)}}\);
\({\text{pH}} = (14 – {\text{pOH}} = 14 – 2.29 = ){\text{ }}11.71\);
Award [2] for correct final answer.
Accept correct answer with more than 2 decimal places.
solution which resists change in pH / changes pH slightly / OWTTE;
when small amounts of acid or base are added;
\({\text{[N}}{{\text{H}}_3}{\text{] = }}\left( {\frac{{(1.50 \times 0.0200) – (0.500 \times 0.0250)}}{{0.0450}} = } \right){\text{ }}0.389{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{)}}\);
\({\text{[NH}}_4^ + {\text{]}} = \left( {\frac{{(0.500 \times 0.0250)}}{{0.0450}} = } \right){\text{ }}0.278{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{)}}\);
\({\text{[O}}{{\text{H}}^ – }{\text{]}} = \left( {\frac{{{K_b}{\text{[N}}{{\text{H}}_3}{\text{]}}}}{{{\text{[NH}}_4^ + {\text{]}}}} = } \right){\text{ }}\frac{{1.78 \times {{10}^{ – 5}} \times 0.389}}{{0.278}} = 2.49 \times {10^{ – 5}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{)}}\);
\({\text{pH}} = (14.0 – {\text{pOH}} = 14.0 – 4.60 = ){\text{ }}9.40\);
OR
\({\text{pOH}} = {\text{p}}{K_b} + \log \frac{{[{\text{NH}}_4^ + ]}}{{{\text{[N}}{{\text{H}}_3}]}}{\text{ = p}}{K_{\text{b}}} + \log \frac{{(12.5/1000)}}{{(17.5/1000)}}\);
\({\text{pOH}} = 4.75 + \log \left( {\frac{{12.5}}{{17.5}}} \right) = 4.75 – 0.146 = 4.604\);
\({\text{pH}} = 14.0 – 4.604 = 9.40\);
Award [4] for the correct final answer.
\(\left( {{\text{V(N}}{{\text{H}}_{\text{3}}}{\text{)}} = \frac{{25.0 \times 0.500}}{{1.50}} = 8.33{\text{ c}}{{\text{m}}^3}} \right)\)
\({\text{V}} = {\text{V(N}}{{\text{H}}_3}{\text{)}} + {\text{V(HCl)}} = 8.33 + 25.0 = 33.3{\text{ c}}{{\text{m}}^3}/0.0333{\text{ d}}{{\text{m}}^3}\);
(\({\text{NH}}_{\text{4}}^ + \) ions are present at equivalence point \({\text{N}}{{\text{H}}_3} + {\text{HCl}} \to {\text{NH}}_4^ + + {\text{C}}{{\text{l}}^ – }\) at equivalence \({\text{n}}({\text{NH}}_4^ + {\text{ produced}}) = {\text{n}}({\text{N}}{{\text{H}}_3}{\text{ added}}) = {\text{n(HCl)}}\))
\([{\text{NH}}_4^ + ] = \frac{{0.500 \times 0.0250}}{{0.0333}} = 0.375{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}})\);
\({\text{(NH}}_4^ + {\text{(aq)}} \rightleftharpoons {\text{N}}{{\text{H}}_3}{\text{(aq)}} + {{\text{H}}^ + }{\text{(aq)}}/{\text{NH}}_4^ + {\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{N}}{{\text{H}}_3}{\text{(aq)}} + {{\text{H}}_3}{{\text{O}}^ + }{\text{(aq)}}\)
\({\text{p}}{K_{\text{a}}}{\text{(NH}}_4^ + ) = 14 – {\text{p}}{K_{\text{b}}}{\text{(N}}{{\text{H}}_3}) = 14.00 – 4.75 = 9.25)\)
\({K_{\text{a}}} = \frac{{{\text{[N}}{{\text{H}}_3}{\text{(aq)][}}{{\text{H}}^ + }{\text{(aq)]}}}}{{{\text{[NH}}_4^ + {\text{(aq)]}}}} = 5.62 \times {10^{ – 10}}\);
\({\text{[}}{{\text{H}}^ + }{\text{(aq)]}} = \sqrt {5.62 \times {{10}^{ – 10}} \times 0.375} = 1.45 \times {10^{ – 5}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{)}}\);
\({\text{pH}} = 4.84\);
Award [4] for the correct final answer.
bromocresol green / methyl red;
ECF for answer in 7(c)(v) if pH given is below 7.
Examiners report
The construction and use of equilibrium expressions for \({K_{\text{c}}}\) showed good understanding. The prediction of the effect of increasing pressure on the position of equilibria by applying Le Chatelier’s principle was good, but the fact that \({K_{\text{c}}}\) remains constant at fixed temperatures was less well known.
pH calculations in c(i), c(ii) and c(v) tended to be very good or completely incorrect.
The construction and use of equilibrium expressions for \({K_{\text{c}}}\) showed good understanding. The prediction of the effect of increasing pressure on the position of equilibria by applying Le Chatelier’s principle was good, but the fact that \({K_{\text{c}}}\) remains constant at fixed temperatures was less well known.
pH calculations in c(i), c(ii) and c(v) tended to be very good or completely incorrect.
The construction and use of equilibrium expressions for \({K_{\text{c}}}\) showed good understanding. The prediction of the effect of increasing pressure on the position of equilibria by applying Le Chatelier’s principle was good, but the fact that \({K_{\text{c}}}\) remains constant at fixed temperatures was less well known.
pH calculations in c(i), c(ii) and c(v) tended to be very good or completely incorrect.
The construction and use of equilibrium expressions for \({K_{\text{c}}}\) showed good understanding. The prediction of the effect of increasing pressure on the position of equilibria by applying Le Chatelier’s principle was good, but the fact that \({K_{\text{c}}}\) remains constant at fixed temperatures was less well known.
pH calculations in c(i), c(ii) and c(v) tended to be very good or completely incorrect.
The construction and use of equilibrium expressions for \({K_{\text{c}}}\) showed good understanding. The prediction of the effect of increasing pressure on the position of equilibria by applying Le Chatelier’s principle was good, but the fact that \({K_{\text{c}}}\) remains constant at fixed temperatures was less well known.
pH calculations in c(i), c(ii) and c(v) tended to be very good or completely incorrect.
The construction and use of equilibrium expressions for \({K_{\text{c}}}\) showed good understanding. The prediction of the effect of increasing pressure on the position of equilibria by applying Le Chatelier’s principle was good, but the fact that \({K_{\text{c}}}\) remains constant at fixed temperatures was less well known.
pH calculations in c(i), c(ii) and c(v) tended to be very good or completely incorrect.
The construction and use of equilibrium expressions for \({K_{\text{c}}}\) showed good understanding. The prediction of the effect of increasing pressure on the position of equilibria by applying Le Chatelier’s principle was good, but the fact that \({K_{\text{c}}}\) remains constant at fixed temperatures was less well known.
pH calculations in c(i), c(ii) and c(v) tended to be very good or completely incorrect.
The construction and use of equilibrium expressions for \({K_{\text{c}}}\) showed good understanding. The prediction of the effect of increasing pressure on the position of equilibria by applying Le Chatelier’s principle was good, but the fact that \({K_{\text{c}}}\) remains constant at fixed temperatures was less well known.
pH calculations in c(i), c(ii) and c(v) tended to be very good or completely incorrect.
| Marks available | 4 |
| Reference code | 14M.2.hl.TZ2.5 |
Question
Bleaches in which chlorine is the active ingredient are the most common, although some environmental groups have concerns about their use.
In aqueous chlorine the equilibrium below produces chloric(I) acid (hypochlorous acid), HOCl, the active bleach.
\[{\text{C}}{{\text{l}}_2}{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{HOCl(aq)}} + {{\text{H}}^ + }{\text{(aq)}} + {\text{C}}{{\text{l}}^ – }{\text{(aq)}}\]
Aqueous sodium chlorate(I), NaOCl, the most common active ingredient in chlorine based bleaches, oxidizes coloured materials to colourless products while being reduced to the chloride ion. It will also oxidize sulfur dioxide to the sulfate ion.
The standard electrode potential for the reduction of the chlorate(V) ion to the chloride ion is \( + 1.49{\text{ V}}\).
(i) Describe the colour change that occurs when aqueous chlorine is added to aqueous sodium bromide.
(ii) Outline, with the help of a chemical equation, why this reaction occurs.
Chloric(I) acid is a weak acid, but hydrochloric acid is a strong acid. Outline how this is indicated in the equation above.
State a balanced equation for the reaction of chloric(I) acid with water.
Outline, in terms of the equilibrium in aqueous chlorine, why it is dangerous to use an acidic toilet cleaner in combination with this kind of bleach.
Suggest why a covalent molecule, such as chloric(I) acid, is readily soluble in water.
Partial neutralization of chloric(I) acid creates a buffer solution. Given that the \({\text{p}}{K_{\text{a}}}\) of chloric(I) acid is 7.53, determine the pH of a solution that has \({\text{[HOCl]}} = 0.100{\text{ mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) and \({\text{[Cl}}{{\text{O}}^ – }{\text{]}} = 0.0500{\text{ mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\).
Describe, using HIn to represent the indicator in its acid form, why an indicator changes colour when excess alkali is added.
(i) Deduce a balanced equation for the reaction between the chlorate(I) ion and sulfur dioxide from the appropriate half-equations.
(ii) State the initial and final oxidation numbers of both chlorine and sulfur in the final equation.

(i) Define the term standard electrode potential.
(ii) Referring to Table 14 of the Data Booklet, deduce, giving a reason, whether the oxidation of the chromium(III) ion to the dichromate(VI) ion by the chlorate(V) ion is energetically feasible.
Markscheme
(i) from (pale) green/colourless to yellow/orange/brown;
Initial colour must be stated.
Do not accept “clear/transparent” instead of “colourless”.
(ii) chlorine more reactive/more powerful oxidizing agent (than bromine);
Accept opposite statements for bromine.
Accept “chloride ion a weaker reducing agent” / “bromide ion a stronger reducing agent”.
Accept “chlorine more electronegative than bromine”.
\({\text{C}}{{\text{l}}_2}{\text{(aq)}} + {\text{2NaBr(aq)}} \to {\text{B}}{{\text{r}}_2}{\text{(aq)}} + {\text{2NaCl(aq)}}/{\text{C}}{{\text{l}}_2}{\text{(aq)}} + {\text{2B}}{{\text{r}}^ – }{\text{(aq)}} \to {\text{B}}{{\text{r}}_2}{\text{(aq)}} + {\text{2C}}{{\text{l}}^ – }{\text{(aq)}}\);
Ignore state symbols.
Do not accept with equilibrium sign.
chloric(I) acid (shown as) a molecule/molecular, but hydrochloric acid (shown as being) split into ions / OWTTE;
Accept “chloric(I) acid is partially dissociated and hydrochloric acid is fully dissociated”.
Reference needed to both acids for mark.
\({\text{HOCl(aq)}} \rightleftharpoons {{\text{H}}^ + }{\text{(aq)}} + {\text{Cl}}{{\text{O}}^ – }{\text{(aq)}}/{\text{HOCl(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {{\text{H}}_3}{{\text{O}}^ + }{\text{(aq)}} + {\text{Cl}}{{\text{O}}^ – }{\text{(aq)}}\);
Equilibrium sign required for the mark.
Ignore state symbols.
acid displaces the equilibrium to the left (to form chlorine);
chlorine is toxic/poisonous/harmful/lung irritant;
Accept answers that refer to the (b) (ii) equilibrium.
chloric(I) acid has –OH group / hydrogen attached to a very electronegative atom;
Accept polar molecule.
can form hydrogen bonds to water;
hydrogen bonding to water increases its solubility;
(as a weak acid it is) in equilibrium with ions;
\({K_{\text{a}}} = {10^{ – 7.53}} = 2.95 \times {10^{ – 8}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}})\);
\({K_{\text{a}}} = \frac{{{\text{[}}{{\text{H}}^ + }{\text{][Cl}}{{\text{O}}^ – }{\text{]}}}}{{{\text{[HOCl]}}}} = \frac{{{\text{[}}{{\text{H}}^ + }{\text{](0.05)}}}}{{{\text{(0.1)}}}} \approx \frac{{{\text{[}}{{\text{H}}^ + }{\text{]}}}}{2} = {\text{2.95}} \times {\text{1}}{{\text{0}}^{ – 8}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{)}}\);
\({\text{[}}{{\text{H}}^ + }{\text{]}} = 2 \times 2.95 \times {10^{ – 8}} = 5.9 \times {10^{ – 8}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{)}}\);
\({\text{pH}} = – \log (5.9 \times {10^{ – 8}}) = 7.23\);
Accept other methods of carrying out the calculation.
Award [4] for correct final answer.
\({\text{HIn}} \rightleftharpoons {{\text{H}}^ + } + {\text{I}}{{\text{n}}^ – }\);
Do not accept equation without equilibrium arrow.
(weak acid in which the) acid/HIn and conjugate base/In– have different colours / OWTTE;
excess alkali shifts the equilibrium to the RHS/towards the conjugate base;
(i) \({\text{Cl}}{{\text{O}}^ – }{\text{(aq)}} + {\text{2}}{{\text{H}}^ + }{\text{(aq)}} + {\text{2}}{{\text{e}}^ – } \rightleftharpoons {{\text{H}}_2}{\text{O(l)}} + {\text{C}}{{\text{l}}^ – }{\text{(aq)}}\);
\({\text{SO}}_4^{2 – }{\text{(aq)}} + {\text{4}}{{\text{H}}^ + }{\text{(aq)}} + {\text{2}}{{\text{e}}^ – } \rightleftharpoons {\text{S}}{{\text{O}}_2}{\text{(aq)}} + {\text{2}}{{\text{H}}_2}{\text{O(l)}}\);
Accept SO42–(aq) + 4H+(aq) + 2e– \( \rightleftharpoons \) H2SO3(aq) + H2O(l).
For final equation:
\({\text{Cl}}{{\text{O}}^ – }{\text{(aq)}} + {\text{S}}{{\text{O}}_2}{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{SO}}_4^{2 – }{\text{(aq)}} + {\text{2}}{{\text{H}}^ + }{\text{(aq)}} + {\text{C}}{{\text{l}}^ – }{\text{(aq)}}\)
Accept ClO–(aq) + H2SO3(aq) \( \rightleftharpoons \) SO42–(aq) + 2H+(aq) + Cl–(aq).
correct reactants and products;
balancing and cancelling \({{\text{e}}^ – }\), \({{\text{H}}^ + }\) and \({{\text{H}}_2}{\text{O}}\);
Apply ECF if incorrect half-equations written.
Ignore state symbols and absence of equilibrium arrow for all equations and accept inclusion of Na+ in any equation.
(ii) Award [2] for all correct, [1] for 2 or 3 correct.

Remember to apply ECF from final (c) (i) equation.
Penalise incorrect notation (eg, 4 or 4+ rather than +4) once only, so award [1] for a fully correct answer in an incorrect format.
(i) potential (of reduction half-reaction) under standard conditions measured
relative to standard hydrogen electrode/SHE / OWTTE;
Allow “solute concentration of 1 mol dm–3” or “1 bar/1 atm (pressure) for gases” instead of “standard conditions”.
(ii) yes / energetically feasible;
would have a positive \({E_{{\text{cell}}}}\) / chlorate(V) ion stronger oxidizing agent than dichromate(VI) ion / OWTTE;
Examiners report
Though it was the least popular question on the paper, it was still answered, though not very well, by a significant number of students. Correct responses to the colour change required in the first part were rare, though more students could write an appropriate equation and outline why the reaction occurred, even though this was often phrased in terms of electronegativity, rather than reactivity or electrode potential. In part (b) many students seemed to be aware of the difference between strong and weak acids, but few could use this to answer the question asked and frequently, even having displayed this knowledge, were unable to write an equation for the required reaction in water. Unfortunately changes in pagination meant that the phrase “the equilibrium above” in part (b) (iii) may have confused candidates with regard to which particular equilibrium the question referred to. Fortunately both of the equilibria that it could have referred to change in the same direction and students scored well on this, and both would eventually result in the release of chlorine, that a number recognized as a toxic gas. In contrast to Question 1, many students could correctly identify the hydrogen bonding, resulting from the –OH group, as being the reason for the solubility of HOCl in water. An encouraging number of students gained full marks for calculating the pH of the buffer, usually by memorizing the Henderson-Hasselbalch equation and substituting in this. An even greater number of students could accurately explain the mode of action of acid-base indicators. In part (c) very few students could write, much less combine, appropriate half equations, even though the reactants and products were given, but far more could correctly deduce the oxidation numbers of the species involved. In the final part most students had some general idea of what a standard electrode potential was, but in many cases the definitions lacked the detail required. Quite a few students correctly deduced that the oxidation of chromium(III) to dichromate(VI) was energetically feasible and give valid reasons to support this.
Though it was the least popular question on the paper, it was still answered, though not very well, by a significant number of students. Correct responses to the colour change required in the first part were rare, though more students could write an appropriate equation and outline why the reaction occurred, even though this was often phrased in terms of electronegativity, rather than reactivity or electrode potential. In part (b) many students seemed to be aware of the difference between strong and weak acids, but few could use this to answer the question asked and frequently, even having displayed this knowledge, were unable to write an equation for the required reaction in water. Unfortunately changes in pagination meant that the phrase “the equilibrium above” in part (b) (iii) may have confused candidates with regard to which particular equilibrium the question referred to. Fortunately both of the equilibria that it could have referred to change in the same direction and students scored well on this, and both would eventually result in the release of chlorine, that a number recognized as a toxic gas. In contrast to Question 1, many students could correctly identify the hydrogen bonding, resulting from the –OH group, as being the reason for the solubility of HOCl in water. An encouraging number of students gained full marks for calculating the pH of the buffer, usually by memorizing the Henderson-Hasselbalch equation and substituting in this. An even greater number of students could accurately explain the mode of action of acid-base indicators. In part (c) very few students could write, much less combine, appropriate half equations, even though the reactants and products were given, but far more could correctly deduce the oxidation numbers of the species involved. In the final part most students had some general idea of what a standard electrode potential was, but in many cases the definitions lacked the detail required. Quite a few students correctly deduced that the oxidation of chromium(III) to dichromate(VI) was energetically feasible and give valid reasons to support this.
Though it was the least popular question on the paper, it was still answered, though not very well, by a significant number of students. Correct responses to the colour change required in the first part were rare, though more students could write an appropriate equation and outline why the reaction occurred, even though this was often phrased in terms of electronegativity, rather than reactivity or electrode potential. In part (b) many students seemed to be aware of the difference between strong and weak acids, but few could use this to answer the question asked and frequently, even having displayed this knowledge, were unable to write an equation for the required reaction in water. Unfortunately changes in pagination meant that the phrase “the equilibrium above” in part (b) (iii) may have confused candidates with regard to which particular equilibrium the question referred to. Fortunately both of the equilibria that it could have referred to change in the same direction and students scored well on this, and both would eventually result in the release of chlorine, that a number recognized as a toxic gas. In contrast to Question 1, many students could correctly identify the hydrogen bonding, resulting from the –OH group, as being the reason for the solubility of HOCl in water. An encouraging number of students gained full marks for calculating the pH of the buffer, usually by memorizing the Henderson-Hasselbalch equation and substituting in this. An even greater number of students could accurately explain the mode of action of acid-base indicators. In part (c) very few students could write, much less combine, appropriate half equations, even though the reactants and products were given, but far more could correctly deduce the oxidation numbers of the species involved. In the final part most students had some general idea of what a standard electrode potential was, but in many cases the definitions lacked the detail required. Quite a few students correctly deduced that the oxidation of chromium(III) to dichromate(VI) was energetically feasible and give valid reasons to support this.
Though it was the least popular question on the paper, it was still answered, though not very well, by a significant number of students. Correct responses to the colour change required in the first part were rare, though more students could write an appropriate equation and outline why the reaction occurred, even though this was often phrased in terms of electronegativity, rather than reactivity or electrode potential. In part (b) many students seemed to be aware of the difference between strong and weak acids, but few could use this to answer the question asked and frequently, even having displayed this knowledge, were unable to write an equation for the required reaction in water. Unfortunately changes in pagination meant that the phrase “the equilibrium above” in part (b) (iii) may have confused candidates with regard to which particular equilibrium the question referred to. Fortunately both of the equilibria that it could have referred to change in the same direction and students scored well on this, and both would eventually result in the release of chlorine, that a number recognized as a toxic gas. In contrast to Question 1, many students could correctly identify the hydrogen bonding, resulting from the –OH group, as being the reason for the solubility of HOCl in water. An encouraging number of students gained full marks for calculating the pH of the buffer, usually by memorizing the Henderson-Hasselbalch equation and substituting in this. An even greater number of students could accurately explain the mode of action of acid-base indicators. In part (c) very few students could write, much less combine, appropriate half equations, even though the reactants and products were given, but far more could correctly deduce the oxidation numbers of the species involved. In the final part most students had some general idea of what a standard electrode potential was, but in many cases the definitions lacked the detail required. Quite a few students correctly deduced that the oxidation of chromium(III) to dichromate(VI) was energetically feasible and give valid reasons to support this.
Though it was the least popular question on the paper, it was still answered, though not very well, by a significant number of students. Correct responses to the colour change required in the first part were rare, though more students could write an appropriate equation and outline why the reaction occurred, even though this was often phrased in terms of electronegativity, rather than reactivity or electrode potential. In part (b) many students seemed to be aware of the difference between strong and weak acids, but few could use this to answer the question asked and frequently, even having displayed this knowledge, were unable to write an equation for the required reaction in water. Unfortunately changes in pagination meant that the phrase “the equilibrium above” in part (b) (iii) may have confused candidates with regard to which particular equilibrium the question referred to. Fortunately both of the equilibria that it could have referred to change in the same direction and students scored well on this, and both would eventually result in the release of chlorine, that a number recognized as a toxic gas. In contrast to Question 1, many students could correctly identify the hydrogen bonding, resulting from the –OH group, as being the reason for the solubility of HOCl in water. An encouraging number of students gained full marks for calculating the pH of the buffer, usually by memorizing the Henderson-Hasselbalch equation and substituting in this. An even greater number of students could accurately explain the mode of action of acid-base indicators. In part (c) very few students could write, much less combine, appropriate half equations, even though the reactants and products were given, but far more could correctly deduce the oxidation numbers of the species involved. In the final part most students had some general idea of what a standard electrode potential was, but in many cases the definitions lacked the detail required. Quite a few students correctly deduced that the oxidation of chromium(III) to dichromate(VI) was energetically feasible and give valid reasons to support this.
Though it was the least popular question on the paper, it was still answered, though not very well, by a significant number of students. Correct responses to the colour change required in the first part were rare, though more students could write an appropriate equation and outline why the reaction occurred, even though this was often phrased in terms of electronegativity, rather than reactivity or electrode potential. In part (b) many students seemed to be aware of the difference between strong and weak acids, but few could use this to answer the question asked and frequently, even having displayed this knowledge, were unable to write an equation for the required reaction in water. Unfortunately changes in pagination meant that the phrase “the equilibrium above” in part (b) (iii) may have confused candidates with regard to which particular equilibrium the question referred to. Fortunately both of the equilibria that it could have referred to change in the same direction and students scored well on this, and both would eventually result in the release of chlorine, that a number recognized as a toxic gas. In contrast to Question 1, many students could correctly identify the hydrogen bonding, resulting from the –OH group, as being the reason for the solubility of HOCl in water. An encouraging number of students gained full marks for calculating the pH of the buffer, usually by memorizing the Henderson-Hasselbalch equation and substituting in this. An even greater number of students could accurately explain the mode of action of acid-base indicators. In part (c) very few students could write, much less combine, appropriate half equations, even though the reactants and products were given, but far more could correctly deduce the oxidation numbers of the species involved. In the final part most students had some general idea of what a standard electrode potential was, but in many cases the definitions lacked the detail required. Quite a few students correctly deduced that the oxidation of chromium(III) to dichromate(VI) was energetically feasible and give valid reasons to support this.
Though it was the least popular question on the paper, it was still answered, though not very well, by a significant number of students. Correct responses to the colour change required in the first part were rare, though more students could write an appropriate equation and outline why the reaction occurred, even though this was often phrased in terms of electronegativity, rather than reactivity or electrode potential. In part (b) many students seemed to be aware of the difference between strong and weak acids, but few could use this to answer the question asked and frequently, even having displayed this knowledge, were unable to write an equation for the required reaction in water. Unfortunately changes in pagination meant that the phrase “the equilibrium above” in part (b) (iii) may have confused candidates with regard to which particular equilibrium the question referred to. Fortunately both of the equilibria that it could have referred to change in the same direction and students scored well on this, and both would eventually result in the release of chlorine, that a number recognized as a toxic gas. In contrast to Question 1, many students could correctly identify the hydrogen bonding, resulting from the –OH group, as being the reason for the solubility of HOCl in water. An encouraging number of students gained full marks for calculating the pH of the buffer, usually by memorizing the Henderson-Hasselbalch equation and substituting in this. An even greater number of students could accurately explain the mode of action of acid-base indicators. In part (c) very few students could write, much less combine, appropriate half equations, even though the reactants and products were given, but far more could correctly deduce the oxidation numbers of the species involved. In the final part most students had some general idea of what a standard electrode potential was, but in many cases the definitions lacked the detail required. Quite a few students correctly deduced that the oxidation of chromium(III) to dichromate(VI) was energetically feasible and give valid reasons to support this.
Though it was the least popular question on the paper, it was still answered, though not very well, by a significant number of students. Correct responses to the colour change required in the first part were rare, though more students could write an appropriate equation and outline why the reaction occurred, even though this was often phrased in terms of electronegativity, rather than reactivity or electrode potential. In part (b) many students seemed to be aware of the difference between strong and weak acids, but few could use this to answer the question asked and frequently, even having displayed this knowledge, were unable to write an equation for the required reaction in water. Unfortunately changes in pagination meant that the phrase “the equilibrium above” in part (b) (iii) may have confused candidates with regard to which particular equilibrium the question referred to. Fortunately both of the equilibria that it could have referred to change in the same direction and students scored well on this, and both would eventually result in the release of chlorine, that a number recognized as a toxic gas. In contrast to Question 1, many students could correctly identify the hydrogen bonding, resulting from the –OH group, as being the reason for the solubility of HOCl in water. An encouraging number of students gained full marks for calculating the pH of the buffer, usually by memorizing the Henderson-Hasselbalch equation and substituting in this. An even greater number of students could accurately explain the mode of action of acid-base indicators. In part (c) very few students could write, much less combine, appropriate half equations, even though the reactants and products were given, but far more could correctly deduce the oxidation numbers of the species involved. In the final part most students had some general idea of what a standard electrode potential was, but in many cases the definitions lacked the detail required. Quite a few students correctly deduced that the oxidation of chromium(III) to dichromate(VI) was energetically feasible and give valid reasons to support this.
Though it was the least popular question on the paper, it was still answered, though not very well, by a significant number of students. Correct responses to the colour change required in the first part were rare, though more students could write an appropriate equation and outline why the reaction occurred, even though this was often phrased in terms of electronegativity, rather than reactivity or electrode potential. In part (b) many students seemed to be aware of the difference between strong and weak acids, but few could use this to answer the question asked and frequently, even having displayed this knowledge, were unable to write an equation for the required reaction in water. Unfortunately changes in pagination meant that the phrase “the equilibrium above” in part (b) (iii) may have confused candidates with regard to which particular equilibrium the question referred to. Fortunately both of the equilibria that it could have referred to change in the same direction and students scored well on this, and both would eventually result in the release of chlorine, that a number recognized as a toxic gas. In contrast to Question 1, many students could correctly identify the hydrogen bonding, resulting from the –OH group, as being the reason for the solubility of HOCl in water. An encouraging number of students gained full marks for calculating the pH of the buffer, usually by memorizing the Henderson-Hasselbalch equation and substituting in this. An even greater number of students could accurately explain the mode of action of acid-base indicators. In part (c) very few students could write, much less combine, appropriate half equations, even though the reactants and products were given, but far more could correctly deduce the oxidation numbers of the species involved. In the final part most students had some general idea of what a standard electrode potential was, but in many cases the definitions lacked the detail required. Quite a few students correctly deduced that the oxidation of chromium(III) to dichromate(VI) was energetically feasible and give valid reasons to support this.
| Marks available | 4 |
| Reference code | 15M.2.hl.TZ1.8 |
Question
Acids can be described as strong or weak.
(i) Outline the difference in dissociation between strong and weak acids of the same concentration.
(ii) Describe three tests that can be carried out in the laboratory, and the expected results, to distinguish between \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{ HCl(aq)}}\) and \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{ C}}{{\text{H}}_{\text{3}}}{\text{COOH(aq)}}\).
Calculate the pH, using table 15 of the data booklet, of a solution of ethanoic acid made by dissolving 1.40 g of the acid in distilled water to make a \({\text{500 c}}{{\text{m}}^{\text{3}}}\) solution.
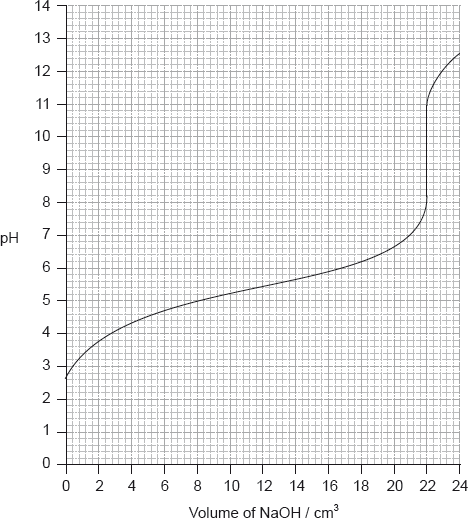
Determine the pH at the equivalence point of the titration and the \({\text{p}}{K_{\text{a}}}\) of an unknown acid using the acid-base titration curve below.
Identify, using table 16 of the data booklet, a suitable indicator to show the end-point of this titration.
Describe how an indicator, that is a weak acid, works. Use Le Chatelier’s principle in your answer.
State the formula of the conjugate base of chloroethanoic acid, \({\text{C}}{{\text{H}}_{\text{2}}}{\text{ClCOOH}}\).
Identify, with a reason, whether chloroethanoic acid is weaker or stronger than ethanoic acid using table 15 of the data booklet.
Determine the pH of the solution resulting when \({\text{100 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.50 mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) \({\text{C}}{{\text{H}}_{\text{2}}}{\text{ClCOOH}}\) is mixed with \({\text{200 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\) NaOH.
Describe how chlorine’s position in the periodic table is related to its electron arrangement.
\({\text{SC}}{{\text{l}}_{\text{2}}}\) and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) are two sulfur chloride type compounds with sulfur having different oxidation states. Predict the name of the shape, the bond angle and polarity of these molecules.
Markscheme
(i) weak acids dissociate only partially and strong acids (are assumed to) dissociate fully;
(ii) measuring electrical conductivity and strong acids have greater electrical conductivity/weak acids have lower electrical conductivity;
Do not accept conductivity for electrical conductivity.
Accept explanation in terms of lightbulb in circuit.
measure pH/use universal indicator and pH higher for weak acid/pH lower for strong acid;
conduct titration with a strong base and equivalence point higher for weak acid / buffer region for weak acid;
adding a reactive metal/carbonate/hydrogen carbonate and stronger effervescence/faster reaction with strong acids;
Accept converse argument.
Accept correct example.
adding a strong base and strong acid would increase more in temperature/weak acids increase less in temperature;
Accept correct example.
Award [1 max] for three suitable tests without correct results.
Accept specific examples with given strong acid and weak acid.
Accept “addition of \(AgN{O_3}(aq)\) and white precipitate with HCl (aq)”.
Do not accept “smell”.
\(\frac{{1.40}}{{60.06}} = 0.0233{\text{ (mol)}}\,\,\,\)and\(\,\,\,\frac{{0.0233}}{{0.500}} = 0.0466{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}})\);
\({\text{(p}}{K_{\text{a}}} = 4.76{\text{)}}{K_{\text{a}}} = 1.7 \times {10^{ – 5}}\);
\({\text{[}}{{\text{H}}^ + }{\text{]}} = \sqrt {{K_{\text{a}}}{\text{[HA]}}} = 8.9 \times {10^{ – 4}}\);
Accept \(9.0 \times 1{0^{ – {\text{4}}}}\).
\({\text{pH}} = 3.05\);
Award [4] for correct final answer.
Accept alternative methods.
Equivalence point: pH of 9.5;
Accept values between 9 and 10.
\({\text{p}}{K_{\text{a}}} = {\text{pH}}\) at half equivalence point;
\({\text{p}}{K_{\text{a}}} = 5.4\);
Accept any value between 5.2 and 5.6.
Award [2] for M2 and M3 if correct \(p{K_a}\) given without explanation.
phenolphthalein;
\({\text{HIn(aq)}} \rightleftharpoons {{\text{H}}^ + }{\text{(aq)}} + {\text{I}}{{\text{n}}^ – }{\text{(aq)}}\) and HIn and \({\text{I}}{{\text{n}}^ – }\) have different colours;
Ignore state symbols.
equilibrium shifts depending on addition of \({{\text{H}}^ + }\) and \({\text{O}}{{\text{H}}^ – }\) / more HIn in acid/low pH / more \({\text{I}}{{\text{n}}^ – }\) in alkali/high pH;
\({\text{C}}{{\text{H}}_{\text{2}}}{\text{ClCO}}{{\text{O}}^ – }\);
stronger because \({\text{p}}{K_{\text{a}}}\) of chloroethanoic acid is \( < {\text{p}}{K_{\text{a}}}\) of ethanoic acid;
Concentration of acid: \(\frac{{0.030}}{{0.300}} = 0.10{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{)}}\);
Concentration of base/salt: \(\frac{{0.020}}{{0.300}} = 0.067{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{)}}\);
\([{{\text{H}}^ + }] = \frac{{{K_{\text{a}}} \times [{\text{HA}}]}}{{[{{\text{A}}^ – }]}}/\frac{{1.3 \times {{10}^{ – 3}} \times 0.10}}{{0.067}}{\text{/}}1.9 \times {10^{ – 3}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{)}}\);
\({\text{pH}} = 2.72\);
Award [4] for correct final answer.
Accept 2.69, 2.70 or 2.7.
Alternative for M3 and M4 if Henderson-Hasselbalch equation used:
M3: \(pH = p{K_a} + log\frac{{[base]}}{{[acid]}}{\text{/ }}2.87 + log\left( {\frac{{{\text{0.067}}}}{{0.10}}} \right)\)
M4: \(pH = 2.70\).
Award [1 max] for \({n_{acid}} ( = 100 \times 0.50 \div 1000) = 0.050 mol\) and
\({n_{base}}( = 200 \times 0.10 \div 1000) = 0.020 mol\).
Cl has 7 valence electrons and is in group 7;
Accept “group 17” as suggested by IUPAC.
Cl has 3 occupied (electron) shells/energy levels and so is in period 3;
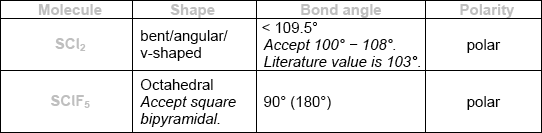
Do not accept ECF for bond angles and polarities from incorrect shapes.
Award [3] for all six correct.
Award [2] for four or five correct.
Award [1] for two or three correct.
Examiners report
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
There is a difference, which candidates should note, between “not fully dissociated” and “partially dissociated” when describing a weak acid. The latter is correct; the former is not accepted as it could mean anything between 1% and 99%. In (ii), many did not state the difference in behaviour of the two acids. Many gained the first mark in (b) for finding the concentration of ethanoic acid. Thereafter either full marks was obtained – or there was total confusion. The equivalence point in (c) was better known than the \({\text{p}}{K_{\text{a}}}\) where an explanation was expected. The best candidates annotated the graph. Almost all candidates identified phenolphthalein in (ii) correctly but in (iii) any answer that did not begin with an equation was likely to score zero. In questions such as (d) (i), candidates should avoid writing a balanced equation (and there were many) unless the actual answer is clearly indicated. Many were able to identify the stronger acid with the correct reason but in (iii) there were few successful conclusions, many not having recognized that a buffer solution was formed. In (e), most were able to explain why chlorine is in group 7, but the explanation for the period, when it was given, often omitted the idea of occupied shells. In (f), it was disappointing to note that many thought \({\text{SC}}{{\text{l}}_{\text{2}}}\) to be linear and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) trigonal bipyramidal or square pyramidal. Two respondents commented that the column headed “polarity” was confusing; although we could have expressed this more clearly, the candidates did not seem to have a difficulty with this.
| Marks available | 4 |
| Reference code | 15M.2.hl.TZ2.4 |
Question
A buffer solution with a pH of 3.87 contains \({\text{7.41 g}}\,{\text{d}}{{\text{m}}^{ – 3}}\) of propanoic acid, \({\text{C}}{{\text{H}}_{\text{3}}}{\text{C}}{{\text{H}}_{\text{2}}}{\text{COOH}}\), together with an unknown quantity of sodium propanoate, \({\text{C}}{{\text{H}}_{\text{3}}}{\text{C}}{{\text{H}}_{\text{2}}}{\text{COONa}}\).
Define the term buffer solution.
Explain, using appropriate equations, how this solution acts as a buffer solution.
Calculate the concentration, in \({\text{mol}}\,{\text{d}}{{\text{m}}^{ – 3}}\), of sodium propanoate in this buffer solution.
The \({\text{p}}{K_{\text{a}}}\) of propanoic acid is 4.87 at 298 K.
Markscheme
a solution that resists changes in pH / changes pH slightly / OWTTE;
when small amounts of an acid/\({{\text{H}}^ + }\) or a base/alkali/\({\text{O}}{{\text{H}}^ – }\) are added;
addition of acid:
\({\text{C}}{{\text{H}}_3}{\text{C}}{{\text{H}}_2}{\text{CO}}{{\text{O}}^ – }{\text{(aq)}} + {{\text{H}}^ + }{\text{(aq)}} \to {\text{C}}{{\text{H}}_3}{\text{C}}{{\text{H}}_2}{\text{COOH(aq)}}\) / propanoate ions combine with \({{\text{H}}^ + }\) ions to form undissociated propanoic acid;
addition of base:
\({\text{C}}{{\text{H}}_3}{\text{C}}{{\text{H}}_2}{\text{COOH(aq)}} + {\text{O}}{{\text{H}}^ – }{\text{(aq)}} \to {\text{C}}{{\text{H}}_3}{\text{C}}{{\text{H}}_2}{\text{CO}}{{\text{O}}^ – }{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}}\) / addition of \({\text{O}}{{\text{H}}^ – }\) removes \({{\text{H}}^ + }\) and more propanoic acid dissociates/ionizes;
Ignore state symbols.
Accept reversible arrows.
Award [1 max] if correct equations are given without reference to addition of acid or alkali.
\({K_{\text{a}}} = \frac{{[{{\text{H}}^ + }{\text{(aq)][C}}{{\text{H}}_3}{\text{C}}{{\text{H}}_2}{\text{CO}}{{\text{O}}^ – }{\text{(aq)]}}}}{{[{\text{C}}{{\text{H}}_3}{\text{C}}{{\text{H}}_2}{\text{COOH(aq)]}}}}/{\text{pH}} = {\text{p}}{K_{\text{a}}} + \log \left( {\frac{{{\text{[base]}}}}{{{\text{[acid]}}}}} \right)\);
\({K_{\text{a}}} = 1.3 \times {10^{ – 5}}/{10^{ – 4.87}}\) and \([{{\text{H}}^ + }] = 1.3 \times {10^{ – 4}}/{10^{ – 3.87}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{) }}/\log \frac{{{\text{[C}}{{\text{H}}_3}{\text{C}}{{\text{H}}_2}{\text{CO}}{{\text{O}}^ – }]}}{{[{\text{C}}{{\text{H}}_3}{\text{C}}{{\text{H}}_2}{\text{COOH]}}}} = 3.87 – 4.87 = – 1\);
\(\left( {[{\text{C}}{{\text{H}}_3}{\text{C}}{{\text{H}}_2}{\text{COOH]}} = \frac{{7.41}}{{74.09}} = } \right)0.100/1.00 \times {10^{ – 1}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}}{\text{)}}\);
\({\text{([C}}{{\text{H}}_3}{\text{C}}{{\text{H}}_2}{\text{COONa]}} = )0.010/1.0 \times {10^{ – 2}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ – 3}})\);
Award [4] for correct final answer.
Accept corresponding use of \({[{H_3}O]^ + }\) for \([{H^ + }]\), [acid] for \([C{H_3}C{H_2}COOH]\), and [base] or [salt] for \([C{H_3}C{H_2}CO{O^ – }]\) throughout.
Examiners report
Most candidates were able to give a definition of buffer solutions including the detail that pH does not change significantly when small amounts of acid or alkali are added. The explanation of the action of buffers proved to be more challenging with only the stronger candidates giving a complete response in terms of protonation of the conjugate base and increased dissociation of the acid. The calculation of equilibrium concentrations from \({\text{p}}{K_{\text{a}}}\) values was better done than in previous sessions, but still proved too difficult for many. The need to change the units of concentration of propanoic acid made this an additional obstacle in this demanding question.
Most candidates were able to give a definition of buffer solutions including the detail that pH does not change significantly when small amounts of acid or alkali are added. The explanation of the action of buffers proved to be more challenging with only the stronger candidates giving a complete response in terms of protonation of the conjugate base and increased dissociation of the acid. The calculation of equilibrium concentrations from \({\text{p}}{K_{\text{a}}}\) values was better done than in previous sessions, but still proved too difficult for many. The need to change the units of concentration of propanoic acid made this an additional obstacle in this demanding question.
Most candidates were able to give a definition of buffer solutions including the detail that pH does not change significantly when small amounts of acid or alkali are added. The explanation of the action of buffers proved to be more challenging with only the stronger candidates giving a complete response in terms of protonation of the conjugate base and increased dissociation of the acid. The calculation of equilibrium concentrations from \({\text{p}}{K_{\text{a}}}\) values was better done than in previous sessions, but still proved too difficult for many. The need to change the units of concentration of propanoic acid made this an additional obstacle in this demanding question.