Question
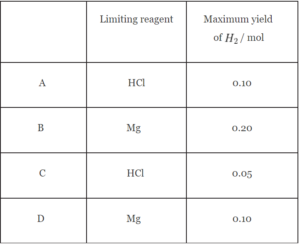
0.20 mol of magnesium is mixed with 0.10 mol of hydrochloric acid.
Mg (s) + 2HCl (aq) → MgC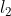
(aq) + 
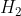(g)
▶️Answer/Explanation
Ans: C
1 mol of Mg requires 2 moles HCl.
0.2 mol Mg will require 0.4 moles HCl.
Since we have only 0.1 mol HCl, hence, it is the limiting reagent.
2 mol HCl forms 1 mol H2.
0.1 mol HCl will form 0.05 mol H2.
Question
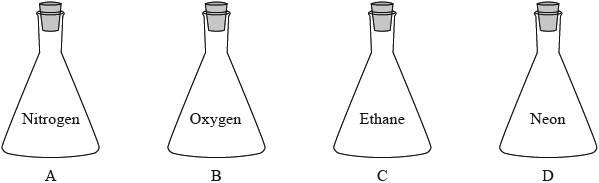
Four identical containers under the same conditions are filled with gases as shown below. Which container and contents will have the highest mass?
▶️Answer/Explanation
B
Since the containers are identical, they will have equal volume of gases hence equal number of moles of gases.
Then, gas having highest molar mass will have highest mass.
Here, Oxygen has highest molar mass (32 g) among these gases.
Question
Under which conditions does \({\text{C}}{{\text{H}}_{\text{4}}}\) have the same number of molecules as \({\text{100 c}}{{\text{m}}^{\text{3}}}\) of \({{\text{O}}_{\text{2}}}\) at 27 °C and \(1.0 \times {10^5}{\text{ Pa}}\)?
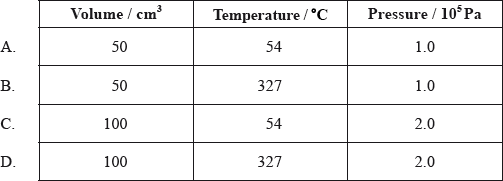
▶️Answer/Explanation
D
\(n= \frac{P\times V}{R\times T}\)
For same number of molecules, number of moles would be same.
For \({{\text{O}}_{\text{2}}}\) , T = 27+273 = 300K
\(n= \frac{10^5\times P\times V}{R\times T}\)
\(n= \frac{10^5\times 1\times 0.1}{R\times 300}\)
For \({\text{C}}{{\text{H}}_{\text{4}}}\)
Option A, \(n= \frac{10^5\times 1\times 0.05}{R\times 327}\)
Option B, \(n= \frac{10^5\times 1\times 0.05}{R\times 600}\)
Option C, \(n= \frac{10^5\times 2\times 0.1}{R\times 327}\)
Option D, \(n= \frac{10^5\times 2\times 0.1}{R\times 600}\) = \(n= \frac{10^5\times 1\times 0.1}{R\times 300}\) = Number of moles of \({{\text{O}}_{\text{2}}}\) .
Question
At which temperature, in K, assuming constant pressure, is the volume of a fixed mass of gas at 127 °C doubled?
A. 200 K
B. 254 K
C. 400 K
D. 800 K
▶️Answer/Explanation
D
PV = nRT
At fixed P and n,
V/T = const
V1/T1=V2/T2
V2 = 2 V1 (Given)
T2/T1 = V2/V1 = 2.
T2 = 2T1
T1 = 127+273 = 400 K
T2 = 800K.
Question
What is the mass, in g, of one molecule of ethane, \({{\text{C}}_{\text{2}}}{{\text{H}}_{\text{6}}}\)?
A. \(3.0 \times {10^{ – 23}}\)
B. \(5.0 \times {10^{ – 23}}\)
C. 30
D. \(1.8 \times {10^{25}}\)
▶️Answer/Explanation
B
1 mole molecules of ethane has 30 g mass.
\(6.0 \times {10^{ 23}}\) molecules ethane = 30 g
1 molecule ethane = 30/(\(6.0 \times {10^{ 23}}\)) = \(5.0 \times {10^{ – 23}}\) g.